山东省泰安市新泰市(五四学制)2024-2025学年六年级下学期期末考试数学试卷(含答案)
文档属性
| 名称 | 山东省泰安市新泰市(五四学制)2024-2025学年六年级下学期期末考试数学试卷(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 759.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(五四学制) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-21 13:23:11 | ||
图片预览




文档简介
山东省泰安市新泰市2024-2025学年六年级下学期7月期末数学试题
一、单选题
1.下列说法:
(1)两点确定一条直线;
(2)画一条射线,使它的长度为;
(3)线段和线段是同一条线段;
(4)射线和射线是同一条射线;
(5)直线和直线是同一条直线.
其中错误的有( )个.
A.1个 B.2个 C.3个 D.4个
2.下列方程中,解为的是( )
A. B. C. D.
3.下列等式变形错误的是( )
A.若,则 B.若,则
C.若,则 D.若,则
4.2024年9月9日,工业和信息化部宣布中国首台氟化氩光刻机,实现套刻技术,标志着我国在高端芯片制造领域取得了关键性进展.已知8纳米米,0.000000008用科学记数法可表示为( )
A. B. C. D.
5.一个蓄水池有的水,以每分钟的速度向池中注水,蓄水池中的水量与注水时间之间的关系式为( )
A. B. C. D.
6.下列计算正确的是( )
A. B. C. D.
7.在解方程时,对该方程进行化简正确的是( )
A. B.
C. D.
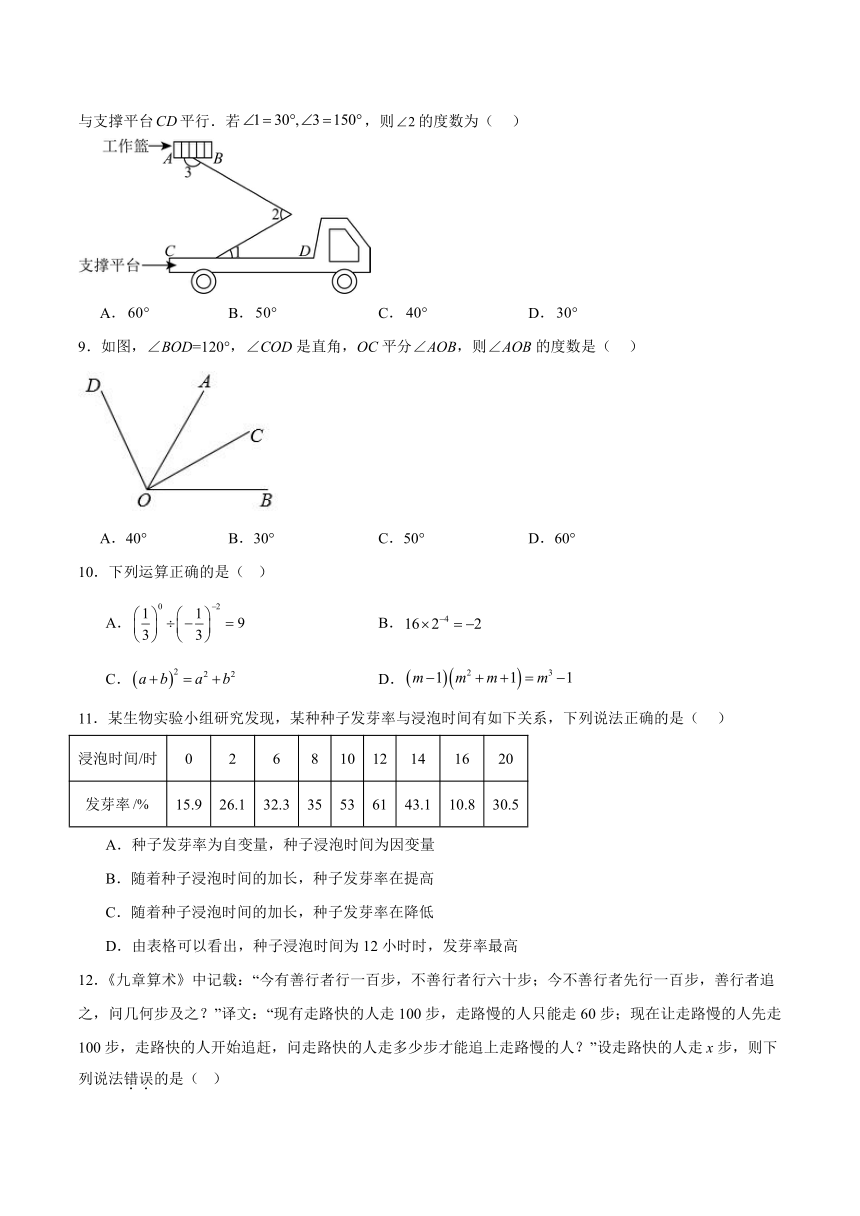
8.在一个由工程车搭建的创意展览场景中,小明站在工程车旁边观察,发现从某个角度看,工作篮底部与支撑平台平行.若,则的度数为( )
A. B. C. D.
9.如图,∠BOD=120°,∠COD是直角,OC平分∠AOB,则∠AOB的度数是( )
A.40° B.30° C.50° D.60°
10.下列运算正确的是( )
A. B.
C. D.
11.某生物实验小组研究发现,某种种子发芽率与浸泡时间有如下关系,下列说法正确的是( )
浸泡时间/时 0 2 6 8 10 12 14 16 20
发芽率 15.9 26.1 32.3 35 53 61 43.1 10.8 30.5
A.种子发芽率为自变量,种子浸泡时间为因变量
B.随着种子浸泡时间的加长,种子发芽率在提高
C.随着种子浸泡时间的加长,种子发芽率在降低
D.由表格可以看出,种子浸泡时间为12小时时,发芽率最高
12.《九章算术》中记载:“今有善行者行一百步,不善行者行六十步;今不善行者先行一百步,善行者追之,问几何步及之?”译文:“现有走路快的人走100步,走路慢的人只能走60步;现在让走路慢的人先走100步,走路快的人开始追赶,问走路快的人走多少步才能追上走路慢的人?”设走路快的人走x步,则下列说法错误的是( )
A.走路快的人和走路慢的人的速度比为 B.可得方程:
C.的值为250 D.可得方程:
二、填空题
13.如图,点,在线段上,,是的中点,若,则 .
14.如图,点在的边上,小明用尺规作出了.
他写出了以下作图过程:
①以为圆心,长为半径画,交于点.
②作射线,则.
③以为圆心,长为半径画弧,交于点.
④以为圆心,任意长为半径画,分别交,于点,.
但他写的顺序排乱了,请你帮他确定正确的顺序是 .(填序号即可)
15.若多项式与的乘积中不含的项,则的值为 .
16.青云镇要修建一条灌溉水渠,如图,水渠从村沿北偏东方向到村,从村沿北偏西方向到村,若水渠从村保持与的方向一致修建,则 .
17.如图1的瓶子中盛满水,如果将这个瓶子中的水全部倒入图2的杯子中,一共需要 个图2这样的杯子.(单位:)(温馨提示:)
三、解答题
18.计算:
(1);
(2);
(3);
(4).
19.如图,甲、乙、丙、丁四个扇形的圆心角度数比为,请完成下面问题:
(1)求出扇形丁的圆心角度数;
(2)如果圆的半径为6,请求出扇形乙的面积(取3).
(3)把圆想像为钟表,当钟表上的钟针指向上午时,时针与分针的夹角是多少度?
20.解方程:
(1);
(2).
21.如图,已知,,,求证:.
证明:,
(_____),
(_______),
又,
,
(_______),
(______).
22.从边长为a的正方形中剪掉一个边长为b的正方形(如图1),然后将剩余部分拼成一个长方形(如图2).
(1)上述操作能验证的等式是_____.(请选择正确的一个)
A. B.
C. D.
(2)当时,则____________;
(3)运用你所得到的公式,计算下列各题:
①;
②.
23.完成下面的证明.
如图,点,分别在,上,连接交于点,已知,,.与平行吗?请说明理由.
24.某校开展校园艺术节系列活动,派小明到文体超市购买若干个文具袋作为奖品.这种文具袋标价每个10元,请认真阅读结账时老板与小明的对话图片,解决下面两个问题:
求小明原计划购买文具袋多少个?
学校决定,再次购买钢笔和签字笔共50支作为补充奖品,其中钢笔标价每支8元,签字笔标价每支6元.经过沟通,这次老板给予8折优惠,合计272元.问小明购买了钢笔和签字笔各多少支?
25.在我市新修建的一条笔直的公路上有、两地,甲、乙二人同时出发,甲从地步行匀速前往地,到达地后,立刻以原速度沿原路返回地.乙从地步行匀速前往地(注意:甲的速度大于乙的速度,乙比甲早到达地,并且甲、乙二人到达地后均停止运动).若甲、乙二人之间的距离(米)与出发时间(分钟)之间的函数关系如图所示,请结合图象解答下列问题:
(1)、两地之间的距离是多少米?
(2)甲、乙二人的步行速度分别是多少米/分?
(3)分别求出a,b,c的值(可直接写出);
(4)在第一次相遇前两人何时相距80米?
参考答案
1.B
解:(1)两点确定一条直线:正确,符合几何公理;
(2)画一条射线,使它的长度为:错误,射线一端无限延伸,无法度量长度;
(3)线段和线段是同一条线段:正确,线段无方向性,端点顺序不影响;
(4)射线和射线是同一条射线:错误,射线以A为端点向B延伸,射线以B为端点向A延伸,方向不同;
(5)直线和直线是同一条直线:正确,直线无方向性,两点确定唯一一条直线.
综上,错误的说法为(2)和(4),一共2个.
故选:B.
2.B
解:A.把代入方程得:左边,右边,左边右边,故此选项不符合题意;
B.把代入方程得:左边,右边,左边右边,故此选项符合题意;
C.把代入方程得:左边,右边,左边右边,故此选项不符合题意;
D.把代入方程得:左边,右边,左边右边,故此选项不符合题意.
故选:B.
3.B
A.若,则,原变形正确,不符合题意;
B.若,则或0,原变形错误,符合题意;
C.若,则,原变形正确,不符合题意;
D.若,则,原变形正确,不符合题意;
故选:B.
4.B
解:,
故选:B.
5.D
解:∵一个蓄水池有的水,以每分钟的速度向池中注水,
∴蓄水池中的水量与注水时间间的函数表达式是:,
故选:D.
6.C
解:A、,故选项A计算错误,此选项不符合题意;
B、,故选项B计算错误,此选项不符合题意;
C、,此选项计算正确,符合题意;
D、 ,故选项D计算错误,此选项不符合题意;
故选:C.
7.B
解:根据分数的基本性质,得:,
故选:B.
8.A
解:如图,过的顶点作直线,将分成和,
∵,
∴,
∴,,
∴,
故选:A.
9.D
解: ∠BOD=120°,∠COD是直角,
OC平分∠AOB,
故选D
10.D
解:A 、(任何非零数的零次方为1),(负指数转化为倒数,平方后符号为正),原式 ,故选项A错误;
B 、,原式 ,故选项B错误;
C 、完全平方公式为 ,缺少中间项,故选项C错误;
D 、,故选项D正确.
故选:D.
11.D
解:A.根据表格分析,种子发芽率为因变量,种子浸泡时间为自变量,故此选项不符合题意;
B.根据表格分析,当浸泡时间小时时,随着种子浸泡时间的加大,种子发芽率在提高,当浸泡时间小时时,随着种子浸泡时间的加大,种子发芽率在降低,故此选项不符合题意;
C.根据表格分析,当浸泡时间小时时,随着种子浸泡时间的加大,种子发芽率在提高,当浸泡时间小时时,随着种子浸泡时间的加大,种子发芽率在降低,故此选项不符合题意;
D.由表格可以看出,当浸泡时间为小时时,种子发芽率最高,所以种子浸泡时间为12小时左右比较适宜, 故此选项符合题意;
故选:D.
12.B
解:选项A: 已知走路快的人走步,走路慢的人走步,相同时间内速度比等于路程比,
∴速度比为,该选项正确.
选项B: 设走路快的人走步,已知速度比为,那么在走路快的人走步的时间内,走路慢的人走的步数是步 ,而走路慢的人先走步,
∴应该是,变形为,而不是,该选项错误.
选项C: 根据方程,交叉相乘得,去括号得,移项可得,即,解得,该选项正确.
选项D: 设走路快的人走步,已知速度比为,根据时间 = 路程÷速度,两人所用时间相等,则,该选项正确.
故选:B.
13.2
解:∵是的中点,,
∴,
∵,
∴,
∴,
故答案为:2.
14.④①③②
解:依题意,先以为圆心,任意长为半径画,分别交,于点,.
再以为圆心,长为半径画,交于点.
然后以为圆心,长为半径画弧,交于点.
最后作射线,则.
故答案为:④①③②
15.
解:
,
∵多项式与的乘积中不含的项,
∴,
∴,
故答案为:.
16.92
解:由题意可知,,
,
与的方向一致,
,
,
故答案为:92.
17.13
解:瓶子中大圆柱的容积为,
瓶子中小圆柱容积,
杯子的容积为,
则所需杯子个数为,
则一共需要13个这样的杯子.
18.(1)
(2)
(3)
(4)
(1)解:
;
(2)解:
;
(3)解:.
.
(4)解:
.
19.(1)
(2)
(3)
(1)解:扇形丁的圆心角度数为:;
(2)解:扇形乙的面积为: ;
(3)钟表上的钟针指向上午时,时针与分针的夹角为:
.
【点睛】本题主要考查了求扇形的圆心角的度数,扇形的面积,以及钟面角,熟练掌握相关知识是解题的关键.
20.(1)
(2)
(1)解: ,
去括号,得,
移项得
合并同类项,得,
将系数化为1,得;
(2)解:,
去分母,得,
去括号,得,
移项得
合并同类项,得,
将系数化为1,得.
21.同旁内角互补,两直线平行;两直线平行,同位角相等;内错角相等,两直线平行;两直线平行,内错角相等
证明:,
(同旁内角互补,两直线平行),
(两直线平行,同位角相等),
又,
,
(内错角相等,两直线平行),
(两直线平行,内错角相等).
故答案为:同旁内角互补,两直线平行;两直线平行,同位角相等;内错角相等,两直线平行;两直线平行,内错角相等.
22.(1)D
(2)2
(3)①1;②
(1)解:根据题意,得剪去小正方形后余下图形的面积为;
重新拼图后得到一个长为,宽为得长方形,则面积为
根据面积不变性质,可得.
故选D.
(2)解:∵,,
∴,
∴.
(3)解:①
;
②
.
23.平行,理由见解析
证明:,
(等式的基本性质),
又,
(等量代换),
(内错角相等,两直线平行),
,
(同旁内角互补,两直线平行),
(平行于同一条直线的两条直线平行).
24.(1)小明原计划购买文具袋17个;(2)小明购买了钢笔20支,签字笔30支.
解:(1)设小明原计划购买文具袋x个,则实际购买了个,
由题意得:.
解得:;
答:小明原计划购买文具袋17个;
(2)设小明购买了钢笔y支,则购买签字笔支,
由题意得:,
解得:,
则:.
答:小明购买了钢笔20支,签字笔30支.
25.(1)1200米
(2)80米/分,60米/分
(3),,
(4)
(1)解:由函数图象可知,最开始时甲乙两人之间的距离为1200米,
∵甲从A地出发,乙从B地出发,两人最开始时的距离就是A、B两地之间的距离,
∴A、B两地之间距离为1200米;
故答案为:1200,60;
(2)解:由图象可知乙经过20分时到达A地,
∴乙的步行速度为(米/分);
由函数图象可知,经过分钟时两人相遇,点M表示此时甲到达B地,乙未到达A地,经过20分钟时乙到达A地,此时两人相距b米,
设甲的步行速度为x米/分,
则,
解得:(米/分)
(3)解:∵由函数图象可知,经过分钟时两人相遇,点M表示此时甲到达B地,乙未到达A地,经过20分钟时乙到达A地,此时两人相距b米,且乙的步行速度为米/分,甲的步行速度为80米/分
∴(分)
∴(米),
(米).
(4)解:设经过x分钟两人第一次相遇前相距80米,
∴,
解得:;
∴经过8分钟两人第一次相遇前相距80米.
一、单选题
1.下列说法:
(1)两点确定一条直线;
(2)画一条射线,使它的长度为;
(3)线段和线段是同一条线段;
(4)射线和射线是同一条射线;
(5)直线和直线是同一条直线.
其中错误的有( )个.
A.1个 B.2个 C.3个 D.4个
2.下列方程中,解为的是( )
A. B. C. D.
3.下列等式变形错误的是( )
A.若,则 B.若,则
C.若,则 D.若,则
4.2024年9月9日,工业和信息化部宣布中国首台氟化氩光刻机,实现套刻技术,标志着我国在高端芯片制造领域取得了关键性进展.已知8纳米米,0.000000008用科学记数法可表示为( )
A. B. C. D.
5.一个蓄水池有的水,以每分钟的速度向池中注水,蓄水池中的水量与注水时间之间的关系式为( )
A. B. C. D.
6.下列计算正确的是( )
A. B. C. D.
7.在解方程时,对该方程进行化简正确的是( )
A. B.
C. D.
8.在一个由工程车搭建的创意展览场景中,小明站在工程车旁边观察,发现从某个角度看,工作篮底部与支撑平台平行.若,则的度数为( )
A. B. C. D.
9.如图,∠BOD=120°,∠COD是直角,OC平分∠AOB,则∠AOB的度数是( )
A.40° B.30° C.50° D.60°
10.下列运算正确的是( )
A. B.
C. D.
11.某生物实验小组研究发现,某种种子发芽率与浸泡时间有如下关系,下列说法正确的是( )
浸泡时间/时 0 2 6 8 10 12 14 16 20
发芽率 15.9 26.1 32.3 35 53 61 43.1 10.8 30.5
A.种子发芽率为自变量,种子浸泡时间为因变量
B.随着种子浸泡时间的加长,种子发芽率在提高
C.随着种子浸泡时间的加长,种子发芽率在降低
D.由表格可以看出,种子浸泡时间为12小时时,发芽率最高
12.《九章算术》中记载:“今有善行者行一百步,不善行者行六十步;今不善行者先行一百步,善行者追之,问几何步及之?”译文:“现有走路快的人走100步,走路慢的人只能走60步;现在让走路慢的人先走100步,走路快的人开始追赶,问走路快的人走多少步才能追上走路慢的人?”设走路快的人走x步,则下列说法错误的是( )
A.走路快的人和走路慢的人的速度比为 B.可得方程:
C.的值为250 D.可得方程:
二、填空题
13.如图,点,在线段上,,是的中点,若,则 .
14.如图,点在的边上,小明用尺规作出了.
他写出了以下作图过程:
①以为圆心,长为半径画,交于点.
②作射线,则.
③以为圆心,长为半径画弧,交于点.
④以为圆心,任意长为半径画,分别交,于点,.
但他写的顺序排乱了,请你帮他确定正确的顺序是 .(填序号即可)
15.若多项式与的乘积中不含的项,则的值为 .
16.青云镇要修建一条灌溉水渠,如图,水渠从村沿北偏东方向到村,从村沿北偏西方向到村,若水渠从村保持与的方向一致修建,则 .
17.如图1的瓶子中盛满水,如果将这个瓶子中的水全部倒入图2的杯子中,一共需要 个图2这样的杯子.(单位:)(温馨提示:)
三、解答题
18.计算:
(1);
(2);
(3);
(4).
19.如图,甲、乙、丙、丁四个扇形的圆心角度数比为,请完成下面问题:
(1)求出扇形丁的圆心角度数;
(2)如果圆的半径为6,请求出扇形乙的面积(取3).
(3)把圆想像为钟表,当钟表上的钟针指向上午时,时针与分针的夹角是多少度?
20.解方程:
(1);
(2).
21.如图,已知,,,求证:.
证明:,
(_____),
(_______),
又,
,
(_______),
(______).
22.从边长为a的正方形中剪掉一个边长为b的正方形(如图1),然后将剩余部分拼成一个长方形(如图2).
(1)上述操作能验证的等式是_____.(请选择正确的一个)
A. B.
C. D.
(2)当时,则____________;
(3)运用你所得到的公式,计算下列各题:
①;
②.
23.完成下面的证明.
如图,点,分别在,上,连接交于点,已知,,.与平行吗?请说明理由.
24.某校开展校园艺术节系列活动,派小明到文体超市购买若干个文具袋作为奖品.这种文具袋标价每个10元,请认真阅读结账时老板与小明的对话图片,解决下面两个问题:
求小明原计划购买文具袋多少个?
学校决定,再次购买钢笔和签字笔共50支作为补充奖品,其中钢笔标价每支8元,签字笔标价每支6元.经过沟通,这次老板给予8折优惠,合计272元.问小明购买了钢笔和签字笔各多少支?
25.在我市新修建的一条笔直的公路上有、两地,甲、乙二人同时出发,甲从地步行匀速前往地,到达地后,立刻以原速度沿原路返回地.乙从地步行匀速前往地(注意:甲的速度大于乙的速度,乙比甲早到达地,并且甲、乙二人到达地后均停止运动).若甲、乙二人之间的距离(米)与出发时间(分钟)之间的函数关系如图所示,请结合图象解答下列问题:
(1)、两地之间的距离是多少米?
(2)甲、乙二人的步行速度分别是多少米/分?
(3)分别求出a,b,c的值(可直接写出);
(4)在第一次相遇前两人何时相距80米?
参考答案
1.B
解:(1)两点确定一条直线:正确,符合几何公理;
(2)画一条射线,使它的长度为:错误,射线一端无限延伸,无法度量长度;
(3)线段和线段是同一条线段:正确,线段无方向性,端点顺序不影响;
(4)射线和射线是同一条射线:错误,射线以A为端点向B延伸,射线以B为端点向A延伸,方向不同;
(5)直线和直线是同一条直线:正确,直线无方向性,两点确定唯一一条直线.
综上,错误的说法为(2)和(4),一共2个.
故选:B.
2.B
解:A.把代入方程得:左边,右边,左边右边,故此选项不符合题意;
B.把代入方程得:左边,右边,左边右边,故此选项符合题意;
C.把代入方程得:左边,右边,左边右边,故此选项不符合题意;
D.把代入方程得:左边,右边,左边右边,故此选项不符合题意.
故选:B.
3.B
A.若,则,原变形正确,不符合题意;
B.若,则或0,原变形错误,符合题意;
C.若,则,原变形正确,不符合题意;
D.若,则,原变形正确,不符合题意;
故选:B.
4.B
解:,
故选:B.
5.D
解:∵一个蓄水池有的水,以每分钟的速度向池中注水,
∴蓄水池中的水量与注水时间间的函数表达式是:,
故选:D.
6.C
解:A、,故选项A计算错误,此选项不符合题意;
B、,故选项B计算错误,此选项不符合题意;
C、,此选项计算正确,符合题意;
D、 ,故选项D计算错误,此选项不符合题意;
故选:C.
7.B
解:根据分数的基本性质,得:,
故选:B.
8.A
解:如图,过的顶点作直线,将分成和,
∵,
∴,
∴,,
∴,
故选:A.
9.D
解: ∠BOD=120°,∠COD是直角,
OC平分∠AOB,
故选D
10.D
解:A 、(任何非零数的零次方为1),(负指数转化为倒数,平方后符号为正),原式 ,故选项A错误;
B 、,原式 ,故选项B错误;
C 、完全平方公式为 ,缺少中间项,故选项C错误;
D 、,故选项D正确.
故选:D.
11.D
解:A.根据表格分析,种子发芽率为因变量,种子浸泡时间为自变量,故此选项不符合题意;
B.根据表格分析,当浸泡时间小时时,随着种子浸泡时间的加大,种子发芽率在提高,当浸泡时间小时时,随着种子浸泡时间的加大,种子发芽率在降低,故此选项不符合题意;
C.根据表格分析,当浸泡时间小时时,随着种子浸泡时间的加大,种子发芽率在提高,当浸泡时间小时时,随着种子浸泡时间的加大,种子发芽率在降低,故此选项不符合题意;
D.由表格可以看出,当浸泡时间为小时时,种子发芽率最高,所以种子浸泡时间为12小时左右比较适宜, 故此选项符合题意;
故选:D.
12.B
解:选项A: 已知走路快的人走步,走路慢的人走步,相同时间内速度比等于路程比,
∴速度比为,该选项正确.
选项B: 设走路快的人走步,已知速度比为,那么在走路快的人走步的时间内,走路慢的人走的步数是步 ,而走路慢的人先走步,
∴应该是,变形为,而不是,该选项错误.
选项C: 根据方程,交叉相乘得,去括号得,移项可得,即,解得,该选项正确.
选项D: 设走路快的人走步,已知速度比为,根据时间 = 路程÷速度,两人所用时间相等,则,该选项正确.
故选:B.
13.2
解:∵是的中点,,
∴,
∵,
∴,
∴,
故答案为:2.
14.④①③②
解:依题意,先以为圆心,任意长为半径画,分别交,于点,.
再以为圆心,长为半径画,交于点.
然后以为圆心,长为半径画弧,交于点.
最后作射线,则.
故答案为:④①③②
15.
解:
,
∵多项式与的乘积中不含的项,
∴,
∴,
故答案为:.
16.92
解:由题意可知,,
,
与的方向一致,
,
,
故答案为:92.
17.13
解:瓶子中大圆柱的容积为,
瓶子中小圆柱容积,
杯子的容积为,
则所需杯子个数为,
则一共需要13个这样的杯子.
18.(1)
(2)
(3)
(4)
(1)解:
;
(2)解:
;
(3)解:.
.
(4)解:
.
19.(1)
(2)
(3)
(1)解:扇形丁的圆心角度数为:;
(2)解:扇形乙的面积为: ;
(3)钟表上的钟针指向上午时,时针与分针的夹角为:
.
【点睛】本题主要考查了求扇形的圆心角的度数,扇形的面积,以及钟面角,熟练掌握相关知识是解题的关键.
20.(1)
(2)
(1)解: ,
去括号,得,
移项得
合并同类项,得,
将系数化为1,得;
(2)解:,
去分母,得,
去括号,得,
移项得
合并同类项,得,
将系数化为1,得.
21.同旁内角互补,两直线平行;两直线平行,同位角相等;内错角相等,两直线平行;两直线平行,内错角相等
证明:,
(同旁内角互补,两直线平行),
(两直线平行,同位角相等),
又,
,
(内错角相等,两直线平行),
(两直线平行,内错角相等).
故答案为:同旁内角互补,两直线平行;两直线平行,同位角相等;内错角相等,两直线平行;两直线平行,内错角相等.
22.(1)D
(2)2
(3)①1;②
(1)解:根据题意,得剪去小正方形后余下图形的面积为;
重新拼图后得到一个长为,宽为得长方形,则面积为
根据面积不变性质,可得.
故选D.
(2)解:∵,,
∴,
∴.
(3)解:①
;
②
.
23.平行,理由见解析
证明:,
(等式的基本性质),
又,
(等量代换),
(内错角相等,两直线平行),
,
(同旁内角互补,两直线平行),
(平行于同一条直线的两条直线平行).
24.(1)小明原计划购买文具袋17个;(2)小明购买了钢笔20支,签字笔30支.
解:(1)设小明原计划购买文具袋x个,则实际购买了个,
由题意得:.
解得:;
答:小明原计划购买文具袋17个;
(2)设小明购买了钢笔y支,则购买签字笔支,
由题意得:,
解得:,
则:.
答:小明购买了钢笔20支,签字笔30支.
25.(1)1200米
(2)80米/分,60米/分
(3),,
(4)
(1)解:由函数图象可知,最开始时甲乙两人之间的距离为1200米,
∵甲从A地出发,乙从B地出发,两人最开始时的距离就是A、B两地之间的距离,
∴A、B两地之间距离为1200米;
故答案为:1200,60;
(2)解:由图象可知乙经过20分时到达A地,
∴乙的步行速度为(米/分);
由函数图象可知,经过分钟时两人相遇,点M表示此时甲到达B地,乙未到达A地,经过20分钟时乙到达A地,此时两人相距b米,
设甲的步行速度为x米/分,
则,
解得:(米/分)
(3)解:∵由函数图象可知,经过分钟时两人相遇,点M表示此时甲到达B地,乙未到达A地,经过20分钟时乙到达A地,此时两人相距b米,且乙的步行速度为米/分,甲的步行速度为80米/分
∴(分)
∴(米),
(米).
(4)解:设经过x分钟两人第一次相遇前相距80米,
∴,
解得:;
∴经过8分钟两人第一次相遇前相距80米.
同课章节目录
