浙教版九年级上册 1.4 二次函数的应用 课件25张
文档属性
| 名称 | 浙教版九年级上册 1.4 二次函数的应用 课件25张 |  | |
| 格式 | pptx | ||
| 文件大小 | 668.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-22 14:03:27 | ||
图片预览






文档简介
(共25张PPT)
1.4 二次函数的应用(1)
第1章 二次函数
浙教版 九年级上册
学习目标
学习目标
1.分析实际问题中变量之间的二次函数关系.(难点)
2.会运用二次函数求实际问题中的最大值或最小值.
3.能应用二次函数的性质解决图形中最大面积问题.(重点)
复习回顾
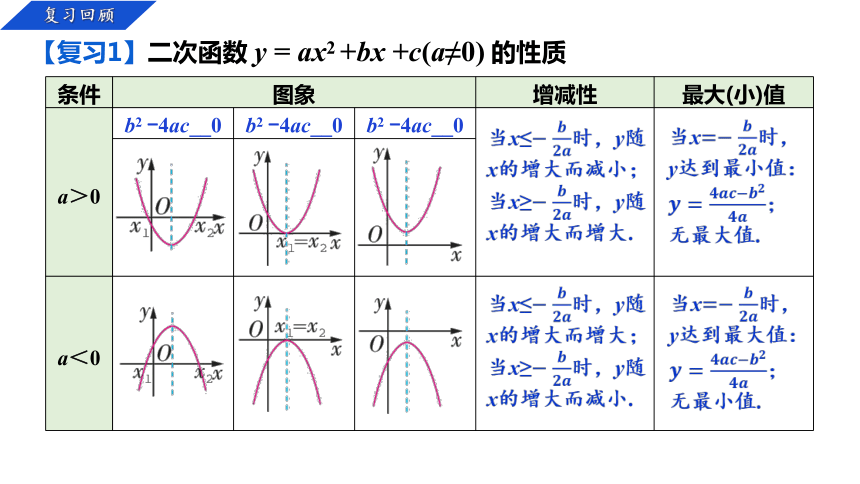
【复习1】二次函数 y = ax2 +bx +c(a≠0) 的性质
条件 图象 增减性 最大(小)值
a>0 b2 -4ac__0 b2 -4ac__0 b2 -4ac__0
a<0
当x≤时,y随x的增大而减小;
当x≥时,y随x的增大而增大.
当x时,
y达到最小值:
;
无最大值.
当x≤时,y随x的增大而增大;
当x≥时,y随x的增大而减小.
当x时,
y达到最大值:
;
无最小值.
复习回顾
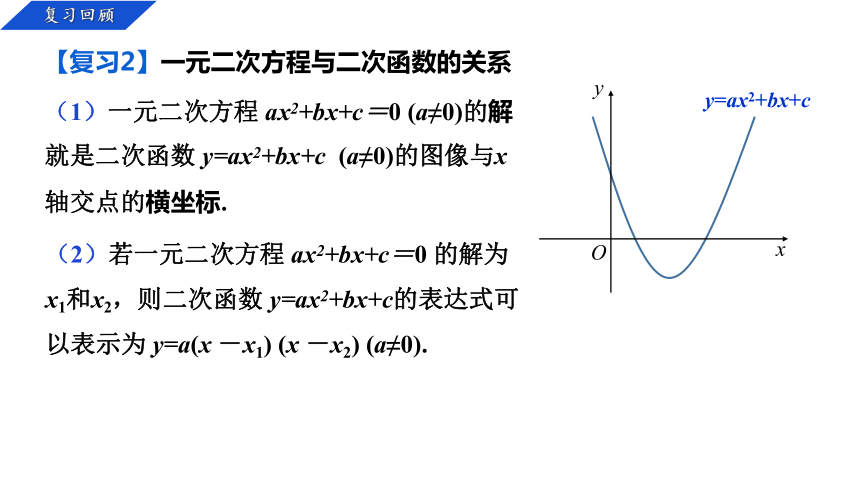
(1)一元二次方程 ax2+bx+c=0 (a≠0)的解就是二次函数 y=ax2+bx+c (a≠0)的图像与x轴交点的横坐标.
y=ax2+bx+c
y
x
O
【复习2】一元二次方程与二次函数的关系
(2)若一元二次方程 ax2+bx+c=0 的解为x1和x2,则二次函数 y=ax2+bx+c的表达式可以表示为 y=a(x -x1) (x -x2) (a≠0).
复习回顾
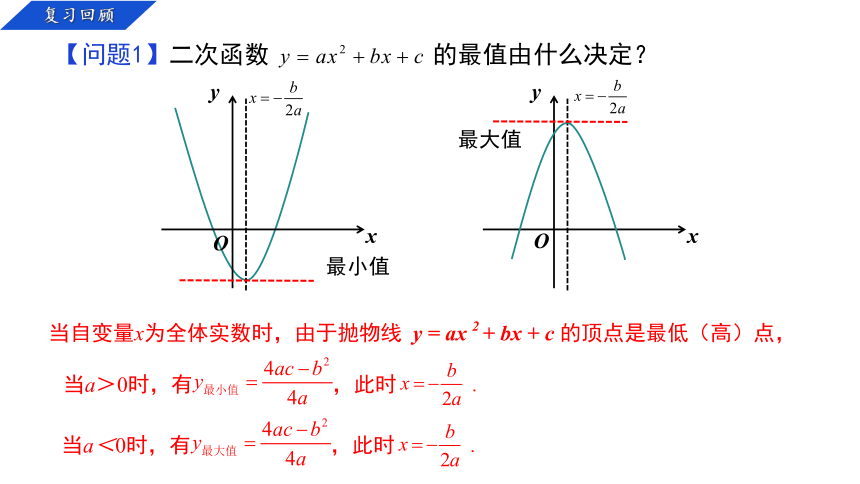
【问题1】二次函数 的最值由什么决定?
x
y
O
x
y
O
最小值
最大值
当自变量x为全体实数时,由于抛物线 y = ax 2 + bx + c 的顶点是最低(高)点,
当a>0时,有 ,此时 .
当a<0时,有 ,此时 .
复习回顾
【练习】求下列函数的最大值或最小值:
(1)配方法
(2)公式法
当x=2时,最小值为3
解:
例题探究
【探究】如图所示,在一面靠墙的空地上用一段长为60m的篱笆围成一个一边靠墙的矩形菜园.
60-2x
x
x
(1)当围墙长为32m时,这个矩形的长、宽各为多少时,菜园的面积最大,最大面积是多少?
解:设垂直于墙的边长为x m,则平行于墙的边长为________m.
则矩形菜园的面积S=______________________.
由0<60 2x≤32,得14≤x<30.
(60 2x)
x(60 2x)= 2x2+60x
∴当x=15m时,S取最大值,此时S=450m2.
∵S= 2x2+60x= 2(x2 30x)= 2(x 15)2+450,
例题探究
【探究】如图所示,在一面靠墙的空地上用一段长为60m的篱笆围成一个一边靠墙的矩形菜园.
60-2x
x
x
(2)当围墙长为18 m时,这个矩形的长、宽各为多少时,菜园的面积最大,最大面积是多少?
解:设垂直于墙的边长为x m,则平行于墙的边长为________m.
则矩形菜园的面积S=______________________.
由0<60 2x≤18,得21≤x<30.
(60 2x)
x(60 2x)= 2x2+60x
∴当 x =21时,S取得最大值,此时S= 2×(21 15)2+450=378m2.
∵S= 2x2+60x= 2(x2 30x)= 2(x 15)2+450,
∵当21≤ x <30时,S随x的增大而减小,
例题探究
二次函数解决几何面积最值问题的方法
(1)求出函数解析式和自变量的取值范围;
(2)配方变形,或利用公式求它的最大值或最小值.
(3)检查求得的最大值或最小值对应的自变量的值必须在自变量的取值范围内.
例题探究
【例1】如图,在Rt△ABC中,∠B=30°,点P在斜边AB上移动,PM⊥BC,PN⊥AC,M,N分别为垂足,AC=1,求矩形PMCN的面积的最大值.
例题探究
学以致用
【例2】九年级某班计划在劳动实践基地内种植蔬菜,班长买回来8米长的围栏,准备围成一边靠墙(墙足够长)的菜园,为了让菜园面积尽可能大,同学们提出了围成矩形、等腰三角形(底边靠墙)、半圆形这三种方案,如图,最佳方案是( )
A.方案1 B.方案2
C.方案3 D.方案1或方案2
学以致用
解:方案1:如图①,
设AD=x米,则AB=(8-2x)米,
则菜园面积=x(8-2x)=-2x2+8x=-2(x-2)2+8(平方米).
当x=2时,菜园面积最大,最大面积为8平方米;
方案2:如图②,过点B作BH⊥AC于H,
则BH ≤ AB=AC=4米.
学以致用
【答案】C
例题探究
【例3】小明准备给长16米,宽12米的长方形空地栽种花卉和草坪,如图Ⅰ,Ⅱ,Ⅲ三个区域分别栽种甲、乙、丙 三种花卉,其余区域栽种草坪.四边形ABCD和四边形EFGH均为正方形,且各有两边与长方形边重合,矩形MFNC(区域Ⅱ)是这两个正方形的重叠部分.
(1)若花卉均价为300元/平方米,栽种花卉的面积为 S平方米,草坪均价为200元/平方米,且花卉和草坪栽种总价不超过43 600元,求S的最大值;
解:长方形空地的面积为16×12=192(平方米).
∵花卉和草坪栽种总价不超过43 600元,
∴300S+200(192-S)≤43 600,解得S≤52.∴S的最大值为52.
例题探究
(2)若矩形MFNC满足MF:FN=1:2.
① 求MF,FN的长;
解:∵ME=16-AD=(16-a)米,
DM=12-FG=12-b=12-(20-a)=(a-8)米,
BN=16-EF=16-b=16-(20-a)=(a-4)米,
NG=12-AB=(12-a)米.
例题探究
例题探究
学以致用
D
A.该函数的最小值是2
B.该函数的最小值是1
C.该函数的最大值是2
D.该函数的最大值是1
学以致用
【2】如图,四边形ABCD的两条对角线AC,BD互相垂直,AC+BD=6,当AC长为________时,四边形ABCD的面积最大.
3
学以致用
【3】已知二次函数y=2x2-4x+5,当-3≤x≤4时,y的最大值是______,最小值是_______.
35
3
【解析】
学以致用
学以致用
【4】在一幅长80 cm,宽50 cm的矩形风景画的四周镶一条金色纸边,制成一幅矩形挂图,如果要使整个挂图的面积是y cm2,设金色纸边的宽为x cm,要求纸边的宽度不得少于1 cm,同时不得超过2 cm.
(1)求出y关于x的函数表达式,并直接写出自变量的取值范围;
(2)此时金色纸边的宽为多少厘米时,这幅挂图的面积最大?求出最大面积的值.
学以致用
课堂小结
二次函数解决几何面积最值问题的方法
(1)求出函数解析式和自变量的取值范围;
(2)配方变形,或利用公式求它的最大值或最小值.
(3)检查求得的最大值或最小值对应的自变量的值必须在自变量的取值范围内.
1.4 二次函数的应用(1)
第1章 二次函数
浙教版 九年级上册
学习目标
学习目标
1.分析实际问题中变量之间的二次函数关系.(难点)
2.会运用二次函数求实际问题中的最大值或最小值.
3.能应用二次函数的性质解决图形中最大面积问题.(重点)
复习回顾
【复习1】二次函数 y = ax2 +bx +c(a≠0) 的性质
条件 图象 增减性 最大(小)值
a>0 b2 -4ac__0 b2 -4ac__0 b2 -4ac__0
a<0
当x≤时,y随x的增大而减小;
当x≥时,y随x的增大而增大.
当x时,
y达到最小值:
;
无最大值.
当x≤时,y随x的增大而增大;
当x≥时,y随x的增大而减小.
当x时,
y达到最大值:
;
无最小值.
复习回顾
(1)一元二次方程 ax2+bx+c=0 (a≠0)的解就是二次函数 y=ax2+bx+c (a≠0)的图像与x轴交点的横坐标.
y=ax2+bx+c
y
x
O
【复习2】一元二次方程与二次函数的关系
(2)若一元二次方程 ax2+bx+c=0 的解为x1和x2,则二次函数 y=ax2+bx+c的表达式可以表示为 y=a(x -x1) (x -x2) (a≠0).
复习回顾
【问题1】二次函数 的最值由什么决定?
x
y
O
x
y
O
最小值
最大值
当自变量x为全体实数时,由于抛物线 y = ax 2 + bx + c 的顶点是最低(高)点,
当a>0时,有 ,此时 .
当a<0时,有 ,此时 .
复习回顾
【练习】求下列函数的最大值或最小值:
(1)配方法
(2)公式法
当x=2时,最小值为3
解:
例题探究
【探究】如图所示,在一面靠墙的空地上用一段长为60m的篱笆围成一个一边靠墙的矩形菜园.
60-2x
x
x
(1)当围墙长为32m时,这个矩形的长、宽各为多少时,菜园的面积最大,最大面积是多少?
解:设垂直于墙的边长为x m,则平行于墙的边长为________m.
则矩形菜园的面积S=______________________.
由0<60 2x≤32,得14≤x<30.
(60 2x)
x(60 2x)= 2x2+60x
∴当x=15m时,S取最大值,此时S=450m2.
∵S= 2x2+60x= 2(x2 30x)= 2(x 15)2+450,
例题探究
【探究】如图所示,在一面靠墙的空地上用一段长为60m的篱笆围成一个一边靠墙的矩形菜园.
60-2x
x
x
(2)当围墙长为18 m时,这个矩形的长、宽各为多少时,菜园的面积最大,最大面积是多少?
解:设垂直于墙的边长为x m,则平行于墙的边长为________m.
则矩形菜园的面积S=______________________.
由0<60 2x≤18,得21≤x<30.
(60 2x)
x(60 2x)= 2x2+60x
∴当 x =21时,S取得最大值,此时S= 2×(21 15)2+450=378m2.
∵S= 2x2+60x= 2(x2 30x)= 2(x 15)2+450,
∵当21≤ x <30时,S随x的增大而减小,
例题探究
二次函数解决几何面积最值问题的方法
(1)求出函数解析式和自变量的取值范围;
(2)配方变形,或利用公式求它的最大值或最小值.
(3)检查求得的最大值或最小值对应的自变量的值必须在自变量的取值范围内.
例题探究
【例1】如图,在Rt△ABC中,∠B=30°,点P在斜边AB上移动,PM⊥BC,PN⊥AC,M,N分别为垂足,AC=1,求矩形PMCN的面积的最大值.
例题探究
学以致用
【例2】九年级某班计划在劳动实践基地内种植蔬菜,班长买回来8米长的围栏,准备围成一边靠墙(墙足够长)的菜园,为了让菜园面积尽可能大,同学们提出了围成矩形、等腰三角形(底边靠墙)、半圆形这三种方案,如图,最佳方案是( )
A.方案1 B.方案2
C.方案3 D.方案1或方案2
学以致用
解:方案1:如图①,
设AD=x米,则AB=(8-2x)米,
则菜园面积=x(8-2x)=-2x2+8x=-2(x-2)2+8(平方米).
当x=2时,菜园面积最大,最大面积为8平方米;
方案2:如图②,过点B作BH⊥AC于H,
则BH ≤ AB=AC=4米.
学以致用
【答案】C
例题探究
【例3】小明准备给长16米,宽12米的长方形空地栽种花卉和草坪,如图Ⅰ,Ⅱ,Ⅲ三个区域分别栽种甲、乙、丙 三种花卉,其余区域栽种草坪.四边形ABCD和四边形EFGH均为正方形,且各有两边与长方形边重合,矩形MFNC(区域Ⅱ)是这两个正方形的重叠部分.
(1)若花卉均价为300元/平方米,栽种花卉的面积为 S平方米,草坪均价为200元/平方米,且花卉和草坪栽种总价不超过43 600元,求S的最大值;
解:长方形空地的面积为16×12=192(平方米).
∵花卉和草坪栽种总价不超过43 600元,
∴300S+200(192-S)≤43 600,解得S≤52.∴S的最大值为52.
例题探究
(2)若矩形MFNC满足MF:FN=1:2.
① 求MF,FN的长;
解:∵ME=16-AD=(16-a)米,
DM=12-FG=12-b=12-(20-a)=(a-8)米,
BN=16-EF=16-b=16-(20-a)=(a-4)米,
NG=12-AB=(12-a)米.
例题探究
例题探究
学以致用
D
A.该函数的最小值是2
B.该函数的最小值是1
C.该函数的最大值是2
D.该函数的最大值是1
学以致用
【2】如图,四边形ABCD的两条对角线AC,BD互相垂直,AC+BD=6,当AC长为________时,四边形ABCD的面积最大.
3
学以致用
【3】已知二次函数y=2x2-4x+5,当-3≤x≤4时,y的最大值是______,最小值是_______.
35
3
【解析】
学以致用
学以致用
【4】在一幅长80 cm,宽50 cm的矩形风景画的四周镶一条金色纸边,制成一幅矩形挂图,如果要使整个挂图的面积是y cm2,设金色纸边的宽为x cm,要求纸边的宽度不得少于1 cm,同时不得超过2 cm.
(1)求出y关于x的函数表达式,并直接写出自变量的取值范围;
(2)此时金色纸边的宽为多少厘米时,这幅挂图的面积最大?求出最大面积的值.
学以致用
课堂小结
二次函数解决几何面积最值问题的方法
(1)求出函数解析式和自变量的取值范围;
(2)配方变形,或利用公式求它的最大值或最小值.
(3)检查求得的最大值或最小值对应的自变量的值必须在自变量的取值范围内.
同课章节目录
