浙教版九年级上册 3.3 垂径定理 课件 21张
文档属性
| 名称 | 浙教版九年级上册 3.3 垂径定理 课件 21张 |  | |
| 格式 | pptx | ||
| 文件大小 | 593.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-22 14:21:58 | ||
图片预览





文档简介
(共21张PPT)
3.3垂径定理(2)
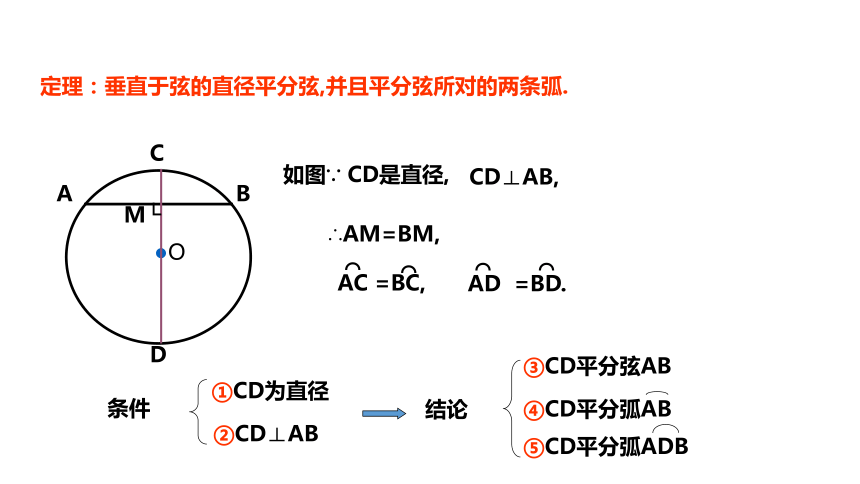
定理:垂直于弦的直径平分弦,并且平分弦所对的两条弧.
●O
A
B
C
D
M└
CD⊥AB,
如图∵ CD是直径,
∴AM=BM,
⌒
⌒
AC =BC,
⌒
⌒
AD =BD.
条件
①CD为直径
②CD⊥AB
⑤CD平分弧ADB
③CD平分弦AB
④CD平分弧AB
结论
垂径定理的逆命题是什么?
条件
结论1
结论2
逆命题1:平分弦的直径垂直于弦。
逆命题2:平分弧的直径垂直于弧所对的弦。
垂直于弦的直径平分弦,并且平分弦所对的两条弧.
在⊙O内任取一点M,请你折出一条弦AB,使AB经过点M,并且AM=BM.
你能说说这样找的理由?
巧手来做一做
●O
●M
垂直于弦的直径平分弦,并且平分弦所对的两条弧.
条件
结论1
结论2
逆命题1:平分弦的直径垂直于弦.
逆命题2:平分弧的直径垂直于弧所对的弦.
垂径定理的逆命题是什么?
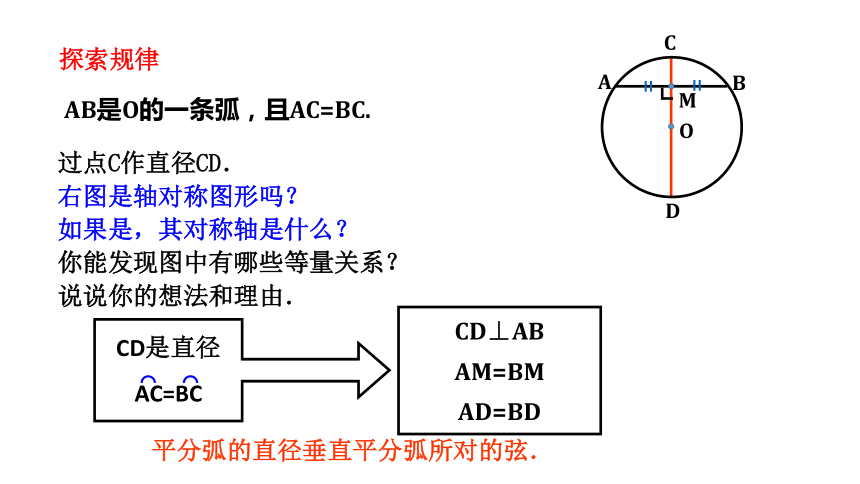
过点C作直径CD.
右图是轴对称图形吗?
如果是,其对称轴是什么?
你能发现图中有哪些等量关系?
说说你的想法和理由.
平分弧的直径垂直平分弧所对的弦.
AB是O的一条弧,且AC=BC.
探索规律
CD⊥AB
AM=BM
AD=BD
CD是直径
AC=BC
C
D
O
M
A
B
┗
⌒
⌒
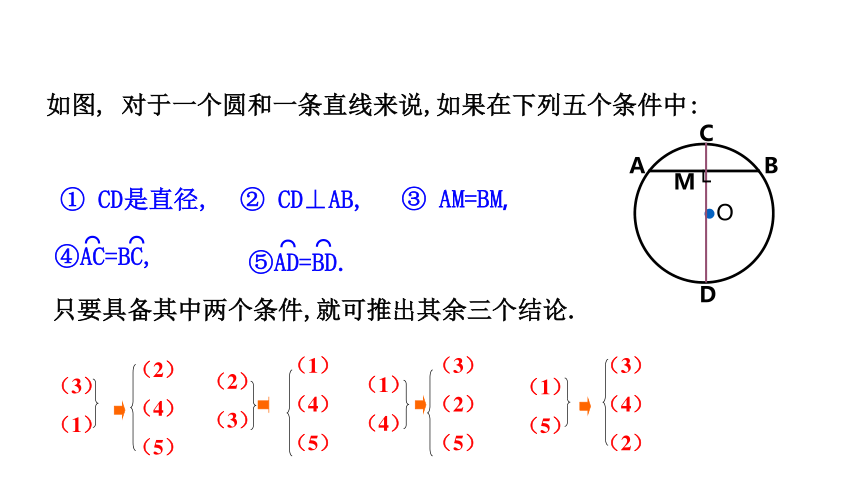
只要具备其中两个条件,就可推出其余三个结论.
① CD是直径,
③ AM=BM,
② CD⊥AB,
⌒
⌒
④AC=BC,
⌒
⌒
⑤AD=BD.
如图, 对于一个圆和一条直线来说,如果在下列五个条件中:
(3)
(1)
(2)
(4)
(5)
(1)
(4)
(5)
(1)
(4)
(3)
(2)
(5)
(1)
(5)
(3)
(4)
(2)
(2)
(3)
●O
A
B
C
D
M└
垂直于弦的直径平分这条弦,并且平分弦所对的弧
逆定理
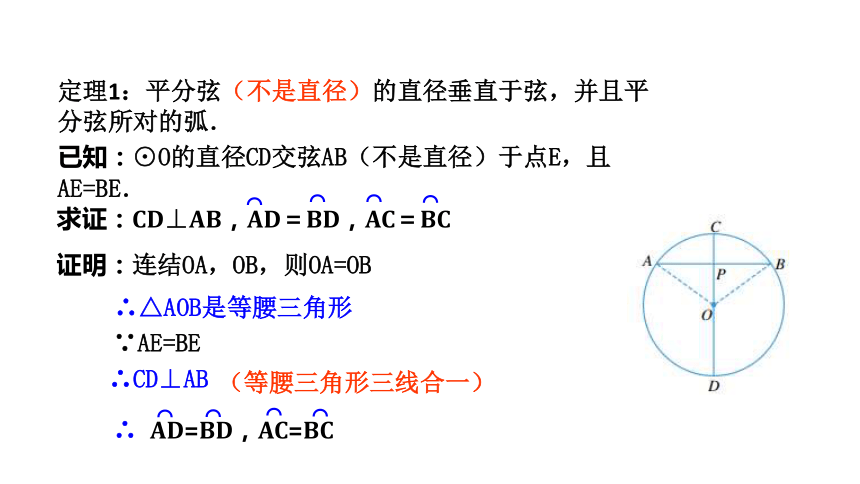
定理1:平分弦(不是直径)的直径垂直于弦,并且平分弦所对的弧.
定理2:平分弧的直径垂直平分弧所对的弦.
垂径定理
已知:⊙O的直径CD交弦AB(不是直径)于点E,且AE=BE.
求证:CD⊥AB,AD=BD,AC=BC
证明:连结OA,OB,则OA=OB
∴△AOB是等腰三角形
∵AE=BE
∴CD⊥AB
(等腰三角形三线合一)
∴ AD=BD,AC=BC
定理1:平分弦(不是直径)的直径垂直于弦,并且平分弦所对的弧.
⌒
⌒
⌒
⌒
⌒
⌒
⌒
⌒
平分弧的直径垂直于弧所对的弦.
已知:如图,⊙O的直径交弦AB(不是直径)于点P,AC=BC
求证:CD⊥AB
⌒
⌒
证明:连结OA,OB,则AO=BO
∴△AOB是等腰三角形
∵AC=BC
⌒
⌒
∴∠AOC=∠BOC
∴CD⊥AB
定理2
新知讲解
例3 赵州桥的跨径(桥拱圆弧所对的弦的长)为 37.02 m,拱高(桥拱圆弧的中点到弦的距离)为7.23m, 求赵州桥的桥拱圆弧的半径(精确到0.01m).
OD=OC-DC=(R-7.23)(m).
在Rt△OAD中,OA2=OD2+AD2
∴R2=18.512+(R-7.23)2,
解得R≈27.31.
答:赵州桥的桥拱圆弧的半径约为27.31m.
AB=37.02m,CD=7.23m,
解:如图,用AB表示桥拱圆弧,设AB所在的圆的圆心为O,半径为R,C为AB的中点,连结OC,交AB于点D,就有OC垂直平分AB,
所以CD就是拱高.由题意,得
课堂练习
1.判断:
⑴垂直于弦的直线平分这条弦,并且平分弦所对的两条弧. ( )
⑵平分弦所对的一条弧的直径一定平分这条弦所对的另一条弧. ( )
⑶经过弦的中点的直径一定垂直于弦. ( )
⑷圆的两条弦所夹的弧相等,则这两条弦平行.( )
⑸弦的垂直平分线一定平分这条弦所对的弧.( )
√
√
10
3.如图,⊙O的半径为5,C是弧AB的中点,且BC=4
那么BA= cm.
4.某一公路隧道的形状如图所示,半圆拱的圆心距离地面2m,半径为1.5m.一辆高3m,宽2.3m的集装箱卡车能顺利通过这个隧道吗 如果要使高度不超过4m,宽为2.3m的大货车也能顺利通过这个隧道,且不改变圆心到地面的距离,半圆拱的半径至少为多少米
O
B
A
解 如图,OB=1.5,OA=1.15,
∵ AB2=OB2-OA2,
∴ AB≈0.96m.
∵ 0.96+2=2.96<3,
∴高为3m,宽为2.3m的集装箱
车不能顺利通过.
由题意,若OA=1.15,AB=4-2=2,
又∵AB2=OB2-OA2,
∴OB≈2.31m.
∴要使高度不超过4m,宽为2.3m的大货车能顺利通过,半圆拱半径
至少为2.31m.
变式:某一公路隧道的形状如图所示,上部分抛物线拱的顶点距离地面4m.一辆高3m,宽2.3m的集装箱卡车能顺利通过这个隧道吗 如果要使高度不超过4m,宽为2.3m的大货车也能顺利通过这个隧道,且不改变下,上部分抛物线拱的顶点距离地面至少为多少米
5.如图所示为某运动会所用的圣火盆的示意图,其中圣火盆高120cm,盆体深20cm,立柱高110cm,CD=60cm.
(1)若曲线ACDB是一段圆弧,试求盆口的口径AB的长.
(2)若曲线ACDB是抛物线的一部分,试求盆口的口径AB的长.
课堂小结
垂径定理的逆定理
定理1:平分弦(不是直径)的直径_____________,并且____________________.
定理2:平分弧的直径_____________弧所对的弦.
垂直于弦
平分弦所对的弧
垂直平分
注意:①直径(过圆心的直线),②垂直于弦,③平分弦,④平分弦所对的优弧,⑤平分弦所对的劣弧,以其中的两个为条件,一定能得出其他三个结论.
圆
圆的轴对称性
垂径定理的逆定理
定理1
定理2
平分弦(不是直径)的直径__________,并且_______弦所对的弧
平分弧的直径_______
弧所对的弦
垂直于弦
平分
垂直平分
课堂小结
3.3垂径定理(2)
定理:垂直于弦的直径平分弦,并且平分弦所对的两条弧.
●O
A
B
C
D
M└
CD⊥AB,
如图∵ CD是直径,
∴AM=BM,
⌒
⌒
AC =BC,
⌒
⌒
AD =BD.
条件
①CD为直径
②CD⊥AB
⑤CD平分弧ADB
③CD平分弦AB
④CD平分弧AB
结论
垂径定理的逆命题是什么?
条件
结论1
结论2
逆命题1:平分弦的直径垂直于弦。
逆命题2:平分弧的直径垂直于弧所对的弦。
垂直于弦的直径平分弦,并且平分弦所对的两条弧.
在⊙O内任取一点M,请你折出一条弦AB,使AB经过点M,并且AM=BM.
你能说说这样找的理由?
巧手来做一做
●O
●M
垂直于弦的直径平分弦,并且平分弦所对的两条弧.
条件
结论1
结论2
逆命题1:平分弦的直径垂直于弦.
逆命题2:平分弧的直径垂直于弧所对的弦.
垂径定理的逆命题是什么?
过点C作直径CD.
右图是轴对称图形吗?
如果是,其对称轴是什么?
你能发现图中有哪些等量关系?
说说你的想法和理由.
平分弧的直径垂直平分弧所对的弦.
AB是O的一条弧,且AC=BC.
探索规律
CD⊥AB
AM=BM
AD=BD
CD是直径
AC=BC
C
D
O
M
A
B
┗
⌒
⌒
只要具备其中两个条件,就可推出其余三个结论.
① CD是直径,
③ AM=BM,
② CD⊥AB,
⌒
⌒
④AC=BC,
⌒
⌒
⑤AD=BD.
如图, 对于一个圆和一条直线来说,如果在下列五个条件中:
(3)
(1)
(2)
(4)
(5)
(1)
(4)
(5)
(1)
(4)
(3)
(2)
(5)
(1)
(5)
(3)
(4)
(2)
(2)
(3)
●O
A
B
C
D
M└
垂直于弦的直径平分这条弦,并且平分弦所对的弧
逆定理
定理1:平分弦(不是直径)的直径垂直于弦,并且平分弦所对的弧.
定理2:平分弧的直径垂直平分弧所对的弦.
垂径定理
已知:⊙O的直径CD交弦AB(不是直径)于点E,且AE=BE.
求证:CD⊥AB,AD=BD,AC=BC
证明:连结OA,OB,则OA=OB
∴△AOB是等腰三角形
∵AE=BE
∴CD⊥AB
(等腰三角形三线合一)
∴ AD=BD,AC=BC
定理1:平分弦(不是直径)的直径垂直于弦,并且平分弦所对的弧.
⌒
⌒
⌒
⌒
⌒
⌒
⌒
⌒
平分弧的直径垂直于弧所对的弦.
已知:如图,⊙O的直径交弦AB(不是直径)于点P,AC=BC
求证:CD⊥AB
⌒
⌒
证明:连结OA,OB,则AO=BO
∴△AOB是等腰三角形
∵AC=BC
⌒
⌒
∴∠AOC=∠BOC
∴CD⊥AB
定理2
新知讲解
例3 赵州桥的跨径(桥拱圆弧所对的弦的长)为 37.02 m,拱高(桥拱圆弧的中点到弦的距离)为7.23m, 求赵州桥的桥拱圆弧的半径(精确到0.01m).
OD=OC-DC=(R-7.23)(m).
在Rt△OAD中,OA2=OD2+AD2
∴R2=18.512+(R-7.23)2,
解得R≈27.31.
答:赵州桥的桥拱圆弧的半径约为27.31m.
AB=37.02m,CD=7.23m,
解:如图,用AB表示桥拱圆弧,设AB所在的圆的圆心为O,半径为R,C为AB的中点,连结OC,交AB于点D,就有OC垂直平分AB,
所以CD就是拱高.由题意,得
课堂练习
1.判断:
⑴垂直于弦的直线平分这条弦,并且平分弦所对的两条弧. ( )
⑵平分弦所对的一条弧的直径一定平分这条弦所对的另一条弧. ( )
⑶经过弦的中点的直径一定垂直于弦. ( )
⑷圆的两条弦所夹的弧相等,则这两条弦平行.( )
⑸弦的垂直平分线一定平分这条弦所对的弧.( )
√
√
10
3.如图,⊙O的半径为5,C是弧AB的中点,且BC=4
那么BA= cm.
4.某一公路隧道的形状如图所示,半圆拱的圆心距离地面2m,半径为1.5m.一辆高3m,宽2.3m的集装箱卡车能顺利通过这个隧道吗 如果要使高度不超过4m,宽为2.3m的大货车也能顺利通过这个隧道,且不改变圆心到地面的距离,半圆拱的半径至少为多少米
O
B
A
解 如图,OB=1.5,OA=1.15,
∵ AB2=OB2-OA2,
∴ AB≈0.96m.
∵ 0.96+2=2.96<3,
∴高为3m,宽为2.3m的集装箱
车不能顺利通过.
由题意,若OA=1.15,AB=4-2=2,
又∵AB2=OB2-OA2,
∴OB≈2.31m.
∴要使高度不超过4m,宽为2.3m的大货车能顺利通过,半圆拱半径
至少为2.31m.
变式:某一公路隧道的形状如图所示,上部分抛物线拱的顶点距离地面4m.一辆高3m,宽2.3m的集装箱卡车能顺利通过这个隧道吗 如果要使高度不超过4m,宽为2.3m的大货车也能顺利通过这个隧道,且不改变下,上部分抛物线拱的顶点距离地面至少为多少米
5.如图所示为某运动会所用的圣火盆的示意图,其中圣火盆高120cm,盆体深20cm,立柱高110cm,CD=60cm.
(1)若曲线ACDB是一段圆弧,试求盆口的口径AB的长.
(2)若曲线ACDB是抛物线的一部分,试求盆口的口径AB的长.
课堂小结
垂径定理的逆定理
定理1:平分弦(不是直径)的直径_____________,并且____________________.
定理2:平分弧的直径_____________弧所对的弦.
垂直于弦
平分弦所对的弧
垂直平分
注意:①直径(过圆心的直线),②垂直于弦,③平分弦,④平分弦所对的优弧,⑤平分弦所对的劣弧,以其中的两个为条件,一定能得出其他三个结论.
圆
圆的轴对称性
垂径定理的逆定理
定理1
定理2
平分弦(不是直径)的直径__________,并且_______弦所对的弧
平分弧的直径_______
弧所对的弦
垂直于弦
平分
垂直平分
课堂小结
同课章节目录
