3.1.2 确定圆的条件及三角形外接圆课件(共19张PPT)浙教版九年级上册
文档属性
| 名称 | 3.1.2 确定圆的条件及三角形外接圆课件(共19张PPT)浙教版九年级上册 |  | |
| 格式 | pptx | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-22 16:06:27 | ||
图片预览




文档简介
(共19张PPT)
第2课时 确定圆的条件及三角形外接圆
3.1 圆
了解不在同一条直线上的三个点确定一个圆,会过不在同一直线上的三个点作圆.
了解三角形的外接圆、三角形的外心及圆的内接三角形的概念.
会过不在同一条直线上的三个点作圆.
有一个圆盘摔碎了,只留下如图所示的一块,现在车间工人要将这个破损的圆盘修复为原来的模样,你有办法复原吗?
课题引入:
知识点
1
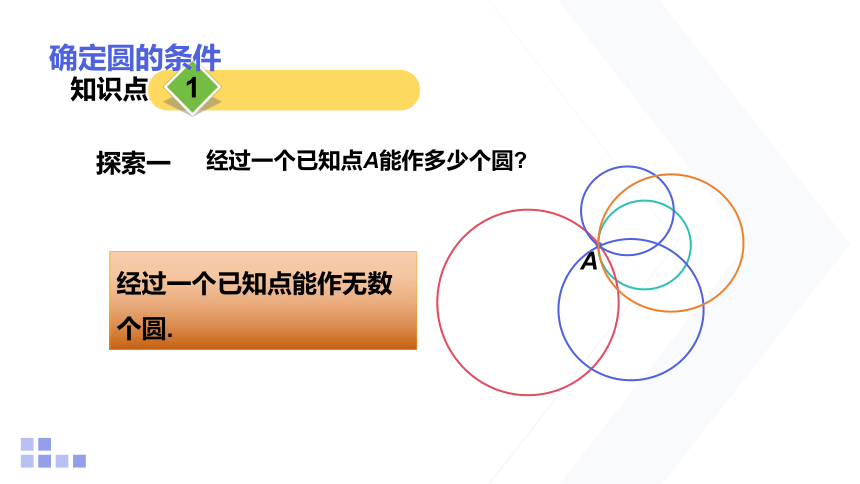
探索一
经过一个已知点A能作多少个圆
A
经过一个已知点能作无数个圆.
确定圆的条件
A
B
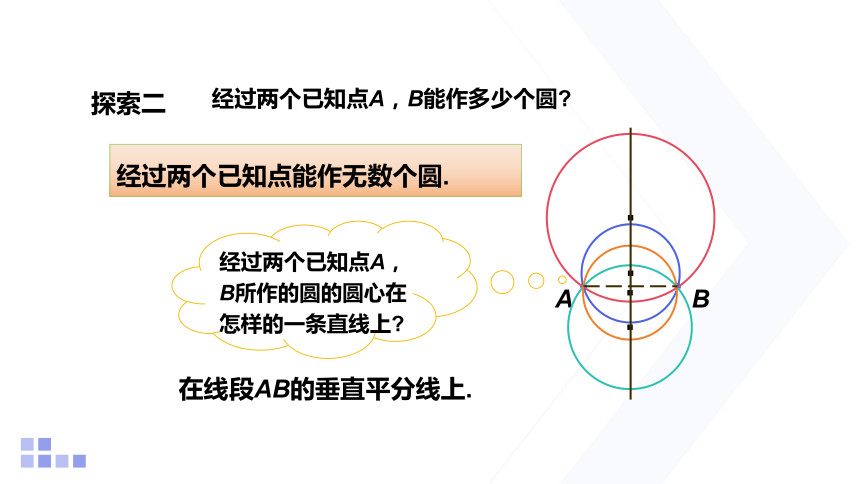
探索二
经过两个已知点A,B能作多少个圆
经过两个已知点能作无数个圆.
·
·
·
·
经过两个已知点A,B所作的圆的圆心在怎样的一条直线上
在线段AB的垂直平分线上.
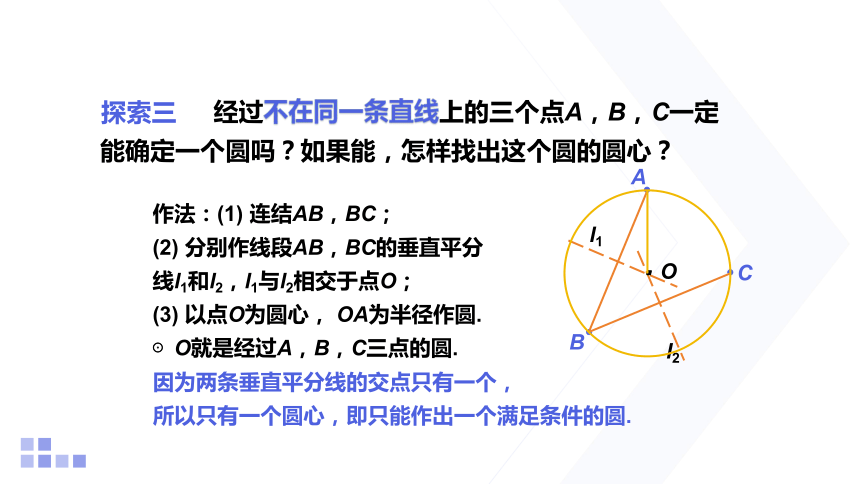
经过不在同一条直线上的三个点A,B,C一定能确定一个圆吗?如果能,怎样找出这个圆的圆心?
探索三
A
B
C
【分析】如图,A,B,C三个点不在同一条直线上,要经过这三个点作圆,就需要确定一个点O作为圆心,使它到A,B,C三点的距离相等.
因此,圆心O既要在线段AB的垂直平分
线上,又要在线段BC(或AC)的垂直平分线上.
A
B
C
作法:(1) 连结AB,BC;
(2) 分别作线段AB,BC的垂直平分线l1和l2,l1与l2相交于点O;
(3) 以点O为圆心, OA为半径作圆.
⊙O就是经过A,B,C三点的圆.
l1
l2
·
O
·
因为两条垂直平分线的交点只有一个,
所以只有一个圆心,即只能作出一个满足条件的圆.
经过不在同一条直线上的三个点A,B,C一定能确定一个圆吗?如果能,怎样找出这个圆的圆心?
探索三
A
B
C
由作图可知,DE∥FG,即DE与FG无交点,
因此,找不到一个点到A,B,C三点的距离相等,
所以过同一条直线上的三个点无法作圆.
不在同一条直线上的三个点确定一个圆.
D
E
F
G
若A,B,C三点在同一直线上呢?
现在你知道怎样将一个如图所示的破损的圆盘复原了吗?
1.找到圆弧所在圆的圆心:
①在圆弧上任取三点A,B,C,连结AB, BC.
②分别作出两条线段的垂直平分线,其交点即为圆心.
2.找到圆的半径,并画出这个圆.
B
A
C
例1
已知△ABC,用直尺和圆规作出过点A、B、C的圆.
A
B
C
O
解:如图所示.
1.分别作线段AB,BC的垂直
平分线,相交于点O.
2.以点O为圆心, OA为半径
作⊙O.
⊙O就是所作的圆.
三角形的外接圆与外心
2
如图,⊙O是△ABC的外接圆,△ABC是⊙O的内接三角形,点O是△ABC的外心.
△ABC的外心是哪三条线的交点?
△ABC的外心是△ABC三条边的垂直平分线的交点.
A
B
C
O
知识点
三角形的外接圆及相关概念
经过三角形各个顶点的圆叫做三角形的外接圆,外接圆的圆心叫做三角形的外心,三角形叫做圆的内接三角形.
概念提练:
分别画一个锐角三角形、直角三角形和钝角三角形,再画出它们的外接圆,它们各自的外心位置有什么不同?
特别提醒
(1) 锐角三角形的外心在三角形内部;直角三角形的外心在三角形斜边中点;钝角三角形的外心在三角形外部.
(2) 任何一个三角形都只有一个外接圆,一个圆有无数个内接三角形.
(3) 三角形的外心到三个顶点的距离相等,等于其外接圆的半径.
在△ABC中,BC=24cm,外心O到BC的距离为6cm,求△ABC的外接圆半径.
例2
·
O
A
B
C
已知Rt△ABC的两直角边为a和b,且a、b是方程
x2-3x+1=0 的两根,求Rt△ABC的外接圆面积.
例3
A
B
C
1.如图,点A,B,C,D均在直线l上,点P在直线l外,则经过其中任意三个点,最多可画出圆的个数为( )
A.3 B.4 C.5 D.6
2.已知⊙O是△ABC的外接圆,则点O是△ABC的( )
A.三条高线的交点
B.三条边的垂直平分线的交点
C.三条中线的交点
D.三个内角的平分线的交点
课堂练习
3.九个相同的等边三角形如图所示,已知点O是一个三角形的外心,则这个三角形是( )
A.△ABC
B.△ABE
C.△ABD
D.△ACE
圆
确定圆的条件
三角形与圆
不在同一直线上的三个点确定一个圆
三角形的外接圆
三角形的外心
圆的内接三角形
确定圆的条件及三角形外接圆
第2课时 确定圆的条件及三角形外接圆
3.1 圆
了解不在同一条直线上的三个点确定一个圆,会过不在同一直线上的三个点作圆.
了解三角形的外接圆、三角形的外心及圆的内接三角形的概念.
会过不在同一条直线上的三个点作圆.
有一个圆盘摔碎了,只留下如图所示的一块,现在车间工人要将这个破损的圆盘修复为原来的模样,你有办法复原吗?
课题引入:
知识点
1
探索一
经过一个已知点A能作多少个圆
A
经过一个已知点能作无数个圆.
确定圆的条件
A
B
探索二
经过两个已知点A,B能作多少个圆
经过两个已知点能作无数个圆.
·
·
·
·
经过两个已知点A,B所作的圆的圆心在怎样的一条直线上
在线段AB的垂直平分线上.
经过不在同一条直线上的三个点A,B,C一定能确定一个圆吗?如果能,怎样找出这个圆的圆心?
探索三
A
B
C
【分析】如图,A,B,C三个点不在同一条直线上,要经过这三个点作圆,就需要确定一个点O作为圆心,使它到A,B,C三点的距离相等.
因此,圆心O既要在线段AB的垂直平分
线上,又要在线段BC(或AC)的垂直平分线上.
A
B
C
作法:(1) 连结AB,BC;
(2) 分别作线段AB,BC的垂直平分线l1和l2,l1与l2相交于点O;
(3) 以点O为圆心, OA为半径作圆.
⊙O就是经过A,B,C三点的圆.
l1
l2
·
O
·
因为两条垂直平分线的交点只有一个,
所以只有一个圆心,即只能作出一个满足条件的圆.
经过不在同一条直线上的三个点A,B,C一定能确定一个圆吗?如果能,怎样找出这个圆的圆心?
探索三
A
B
C
由作图可知,DE∥FG,即DE与FG无交点,
因此,找不到一个点到A,B,C三点的距离相等,
所以过同一条直线上的三个点无法作圆.
不在同一条直线上的三个点确定一个圆.
D
E
F
G
若A,B,C三点在同一直线上呢?
现在你知道怎样将一个如图所示的破损的圆盘复原了吗?
1.找到圆弧所在圆的圆心:
①在圆弧上任取三点A,B,C,连结AB, BC.
②分别作出两条线段的垂直平分线,其交点即为圆心.
2.找到圆的半径,并画出这个圆.
B
A
C
例1
已知△ABC,用直尺和圆规作出过点A、B、C的圆.
A
B
C
O
解:如图所示.
1.分别作线段AB,BC的垂直
平分线,相交于点O.
2.以点O为圆心, OA为半径
作⊙O.
⊙O就是所作的圆.
三角形的外接圆与外心
2
如图,⊙O是△ABC的外接圆,△ABC是⊙O的内接三角形,点O是△ABC的外心.
△ABC的外心是哪三条线的交点?
△ABC的外心是△ABC三条边的垂直平分线的交点.
A
B
C
O
知识点
三角形的外接圆及相关概念
经过三角形各个顶点的圆叫做三角形的外接圆,外接圆的圆心叫做三角形的外心,三角形叫做圆的内接三角形.
概念提练:
分别画一个锐角三角形、直角三角形和钝角三角形,再画出它们的外接圆,它们各自的外心位置有什么不同?
特别提醒
(1) 锐角三角形的外心在三角形内部;直角三角形的外心在三角形斜边中点;钝角三角形的外心在三角形外部.
(2) 任何一个三角形都只有一个外接圆,一个圆有无数个内接三角形.
(3) 三角形的外心到三个顶点的距离相等,等于其外接圆的半径.
在△ABC中,BC=24cm,外心O到BC的距离为6cm,求△ABC的外接圆半径.
例2
·
O
A
B
C
已知Rt△ABC的两直角边为a和b,且a、b是方程
x2-3x+1=0 的两根,求Rt△ABC的外接圆面积.
例3
A
B
C
1.如图,点A,B,C,D均在直线l上,点P在直线l外,则经过其中任意三个点,最多可画出圆的个数为( )
A.3 B.4 C.5 D.6
2.已知⊙O是△ABC的外接圆,则点O是△ABC的( )
A.三条高线的交点
B.三条边的垂直平分线的交点
C.三条中线的交点
D.三个内角的平分线的交点
课堂练习
3.九个相同的等边三角形如图所示,已知点O是一个三角形的外心,则这个三角形是( )
A.△ABC
B.△ABE
C.△ABD
D.△ACE
圆
确定圆的条件
三角形与圆
不在同一直线上的三个点确定一个圆
三角形的外接圆
三角形的外心
圆的内接三角形
确定圆的条件及三角形外接圆
同课章节目录
