22.1.3 第1课时 二次函数y=ax? k的图象和性质 教案(表格式)2025-2026学年度人教版数学九年级上册
文档属性
| 名称 | 22.1.3 第1课时 二次函数y=ax? k的图象和性质 教案(表格式)2025-2026学年度人教版数学九年级上册 |  | |
| 格式 | docx | ||
| 文件大小 | 2.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-22 11:26:20 | ||
图片预览


文档简介
九年级上册教案
22.1.3 二次函数 y = a(x - h)2 + k 的
图象和性质
第1课时 二次函数 y = ax2 + k 的图象和性质
教学内容 第1课时 二次函数 y = ax2 + k 的图象和性质 课时 1
核心素养目标 1.会用描点法画出形如y=ax2+k的二次函数图象; 2.通过观察图象能说出二次函数y=ax2+k的图象特征和性质; 3.在类比探究二次函数y=ax2+k的图象和性质的过程中,进一步体会研究函数图象和性质的基本方法和数形结合的思想
知识目标 1.会用描点法画出y=ax2+k的图象. 2.掌握形如y=ax2+k的二次函数图象的性质,并会应用. 3.理解二次函数y=ax2+k与y=ax2之间的联系.
教学重点 掌握形如y=ax2+k的二次函数图象的性质,并会应用.
教学难点 理解二次函数y=ax2+k与y=ax2之间的联系.
教学准备 课件
教学过程 主要师生活动 设计意图
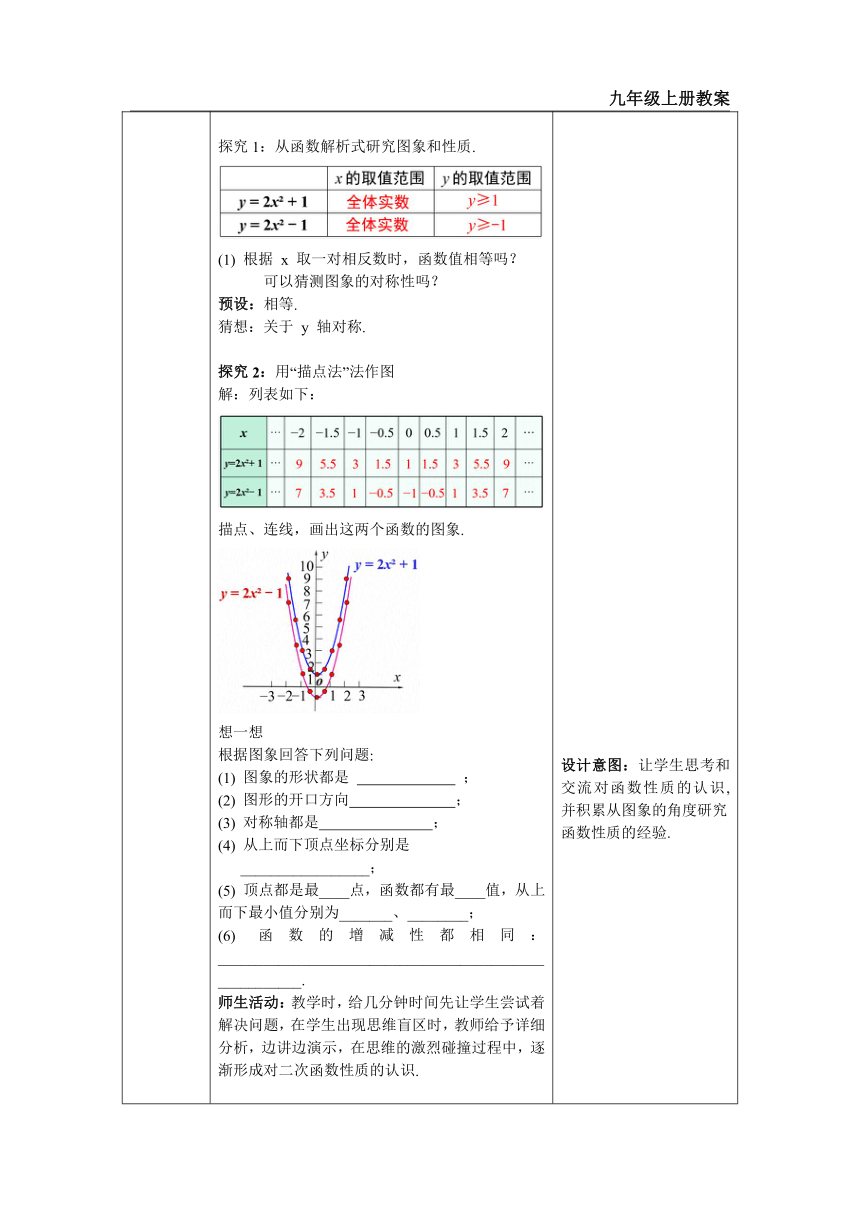
一、情境导入 二、探究新知 当堂练习,巩固所学 一、创设情境,导入新知 类比一次函数: 师生活动:让学生自主回答. (学生积极踊跃发言,问答提出的问题.) 二、小组合作,探究概念和性质 知识点1: 二次函数 y = ax2 + k 的图象和性质 操作与思考1(a>0):在同一直角坐标系中,画出二次函数 y = 2x + 1 , y = 2x - 1 的图象. 师生活动:小组合作学习,尝试从开口方向、对称轴、顶点、最值、增减性等方面描述图象特征和性 质.如果学生在探究过程出现困难,需教师引导学生回顾二次函数y=ax2的相关内容,类比探究. 探究1:从函数解析式研究图象和性质. (1) 根据 x 取一对相反数时,函数值相等吗? 可以猜测图象的对称性吗? 预设:相等. 猜想:关于 y 轴对称. 探究2:用“描点法”法作图 解:列表如下: 描点、连线,画出这两个函数的图象. 想一想 根据图象回答下列问题: (1) 图象的形状都是 ; (2) 图形的开口方向 ; (3) 对称轴都是 ; (4) 从上而下顶点坐标分别是 _________________; (5) 顶点都是最____点,函数都有最____值,从上而下最小值分别为_______、________; (6) 函数的增减性都相同: ______________________________________________________. 师生活动:教学时,给几分钟时间先让学生尝试着解决问题,在学生出现思维盲区时,教师给予详细分析,边讲边演示,在思维的激烈碰撞过程中,逐渐形成对二次函数性质的认识. 预设: (1) 抛物线 (2) 向上 (3) y 轴 (4) (0,1),(0, 1) (5) 低;小;y = 1;y = 1 (6)对称轴左侧 y 随 x 增大而减小, 对称轴右侧 y 随 x 增大而增大 想一想:通过上述例子,函数 y = ax2 + k (a>0) 的性质是什么? 操作与思考2(a<0): 在同一坐标系内画出 y = -2x + 1,y = -2x - 1 的图象并考察它们的开口方向、对称轴和顶点坐标、顶点高低、函数最值、函数增减性. 根据图象回答下列问题: (1) 图象的形状都是 ; (2) 图形的开口方向 ; (3) 对称轴都是 ; (4) 从上而下顶点坐标分别是 _________________; (5)顶点都是最____点,函数都有最____值,从上而下最大值分别为_______、________. (6) 函数的增减性都相同: __________________________ ___________________________. 师生活动:教学时,给几分钟时间先让学生尝试着解决问题,在学生出现思维盲区时,教师给予详细分析,边讲边演示,在思维的激烈碰撞过程中,逐渐形成对二次函数性质的认识. 想一想:通过上述例子,函数 y = ax2 + k (a<0) 的性质是什么? 归纳总结 二次函数 y = ax2 + k (a ≠ 0) 的性质 典例精析 例1 关于二次函数 y = 2x2 + 4,下列说法错误的是 ( ) A.其图象的开口方向向上 B.当 x = 0 时,y 有最大值 4 C.其图象的对称轴是 y 轴 D.其图象的顶点坐标为 (0,4) 分析:当 x = 0 时,y 有最小值 4. 例2 关于抛物线 y = x2 + 1 与 y = x2 1,下列说法正确的是( ) A.开口方向相同 B.顶点相同 C.对称轴相同 D.当 x>0 时,y 随 x 的增大而增大 师生活动:教师给出例题后,让学生独立作业,同时分别选派四名同学上黑板演算. 教师巡视,对学生演算过程中的失误及时予以指正,最后师生共同评析。 知识点2: 二次函数 y = ax2 + k (a≠0) 的图象及平移 做一做:填写下表,画出二次函数 y = 2x , y = 2x2 + 1 ,y = 2x2 1的图象. 观察上述图象,说说它们之间的区别与联系. 想一想 1. 抛物线 y = ax2 + k (a≠0) 与抛物线 y = ax2 有什么关系? 上下平移规律: 二次项不变,常数项上加下减. 链接中考 1. 将二次函数 y = -2x2﹣2 的图象向上平移 3 个单位长度,得到的图象所对应的函数解析式是 . 预设:y = -2x2 + 1 想一想 抛物线 y = ax2 + k (a≠0) 中的 a 决定什么?k 决定什么?它的对称轴是什么?顶点坐标怎样表示? 预设:a 决定开口方向和大小,k 决定顶点的纵坐标;对称轴为 y 轴;顶点坐标为 (0,k). 三、当堂练习,巩固所学 1. 填表: 2. 已知 (m,n) 在 y = ax2 + a (a≠0) 的图象上,则点 ( m,n) ____ (填“在”或“不在”) y = ax2 + a (a≠0) 的图象上. 3. 已知抛物线 y = (a 2)x2 + a2 2 的最高点为 (0,2),则 a =____. 设计意图:类比一次函数,通过平移正比例函数可以得到一般函数,引导学生思考二次函数y=ax2通过平移可以得到哪些函数. 设计意图:类比研究二次函数y=ax2 的方法,从解析式,描点法和图象法三个维度分析二次函数 y = ax2 + k 的图象和性质. 设计意图:让学生思考和交流对函数性质的认识,并积累从图象的角度研究 函数性质的经验. 设计意图:经历从特殊到一般的研究过程,归纳出二次函数y= =ax2+k (a>0) 的图象特征和性质. 设计意图:引导学生类比 研究a>0 时二次函数的方法,归纳当a< 0时二次函数y = ax2 + k的图象特征和性质. 设计意图:加强学生对二次函数y = ax2 + k的图象特征和性质的理解. 设计意图:从数的角度和形的角度读探讨平移之间的关系,让学生学会数形结合的思想,同时经历从特殊到一般的研究过程,得出二次函数y=ax2+k与y=ax2的图象关系. 设计意图:加强学生对二次函数y = ax2 + k的平移性质的理解. 设计意图:帮助学生总结二次函数与系数之间的关系. 设计意图:考查学生对二次函数的性质的掌握. 及时练习巩固,体现学以致用的观念,消除学生学无所用的思想顾虑。
板书设计 第1课时 二次函数 y = ax2 + k 的图象和性质 1.二次函数y=ax2+k的图象与性质: 2.二次函数y=ax2和y=ax2+k的应用.
课后小结 教师与学生一起回顾本节课所学的主要内容,梳理并完善知识思维导图。
教学反思 尝试用描点法画二次函数y=ax2 + k图象,利用多媒体生动形象引导学生总结归纳二次函数y=ax2 + k的性质。内容较为简单,在教学中应鼓励学生积极思考,归纳总结,允许学生回答的不完整,甚至有错误的见解,培养学生乐于分享、发言的习惯,提高学生学习数学的兴趣。
22.1.3 二次函数 y = a(x - h)2 + k 的
图象和性质
第1课时 二次函数 y = ax2 + k 的图象和性质
教学内容 第1课时 二次函数 y = ax2 + k 的图象和性质 课时 1
核心素养目标 1.会用描点法画出形如y=ax2+k的二次函数图象; 2.通过观察图象能说出二次函数y=ax2+k的图象特征和性质; 3.在类比探究二次函数y=ax2+k的图象和性质的过程中,进一步体会研究函数图象和性质的基本方法和数形结合的思想
知识目标 1.会用描点法画出y=ax2+k的图象. 2.掌握形如y=ax2+k的二次函数图象的性质,并会应用. 3.理解二次函数y=ax2+k与y=ax2之间的联系.
教学重点 掌握形如y=ax2+k的二次函数图象的性质,并会应用.
教学难点 理解二次函数y=ax2+k与y=ax2之间的联系.
教学准备 课件
教学过程 主要师生活动 设计意图
一、情境导入 二、探究新知 当堂练习,巩固所学 一、创设情境,导入新知 类比一次函数: 师生活动:让学生自主回答. (学生积极踊跃发言,问答提出的问题.) 二、小组合作,探究概念和性质 知识点1: 二次函数 y = ax2 + k 的图象和性质 操作与思考1(a>0):在同一直角坐标系中,画出二次函数 y = 2x + 1 , y = 2x - 1 的图象. 师生活动:小组合作学习,尝试从开口方向、对称轴、顶点、最值、增减性等方面描述图象特征和性 质.如果学生在探究过程出现困难,需教师引导学生回顾二次函数y=ax2的相关内容,类比探究. 探究1:从函数解析式研究图象和性质. (1) 根据 x 取一对相反数时,函数值相等吗? 可以猜测图象的对称性吗? 预设:相等. 猜想:关于 y 轴对称. 探究2:用“描点法”法作图 解:列表如下: 描点、连线,画出这两个函数的图象. 想一想 根据图象回答下列问题: (1) 图象的形状都是 ; (2) 图形的开口方向 ; (3) 对称轴都是 ; (4) 从上而下顶点坐标分别是 _________________; (5) 顶点都是最____点,函数都有最____值,从上而下最小值分别为_______、________; (6) 函数的增减性都相同: ______________________________________________________. 师生活动:教学时,给几分钟时间先让学生尝试着解决问题,在学生出现思维盲区时,教师给予详细分析,边讲边演示,在思维的激烈碰撞过程中,逐渐形成对二次函数性质的认识. 预设: (1) 抛物线 (2) 向上 (3) y 轴 (4) (0,1),(0, 1) (5) 低;小;y = 1;y = 1 (6)对称轴左侧 y 随 x 增大而减小, 对称轴右侧 y 随 x 增大而增大 想一想:通过上述例子,函数 y = ax2 + k (a>0) 的性质是什么? 操作与思考2(a<0): 在同一坐标系内画出 y = -2x + 1,y = -2x - 1 的图象并考察它们的开口方向、对称轴和顶点坐标、顶点高低、函数最值、函数增减性. 根据图象回答下列问题: (1) 图象的形状都是 ; (2) 图形的开口方向 ; (3) 对称轴都是 ; (4) 从上而下顶点坐标分别是 _________________; (5)顶点都是最____点,函数都有最____值,从上而下最大值分别为_______、________. (6) 函数的增减性都相同: __________________________ ___________________________. 师生活动:教学时,给几分钟时间先让学生尝试着解决问题,在学生出现思维盲区时,教师给予详细分析,边讲边演示,在思维的激烈碰撞过程中,逐渐形成对二次函数性质的认识. 想一想:通过上述例子,函数 y = ax2 + k (a<0) 的性质是什么? 归纳总结 二次函数 y = ax2 + k (a ≠ 0) 的性质 典例精析 例1 关于二次函数 y = 2x2 + 4,下列说法错误的是 ( ) A.其图象的开口方向向上 B.当 x = 0 时,y 有最大值 4 C.其图象的对称轴是 y 轴 D.其图象的顶点坐标为 (0,4) 分析:当 x = 0 时,y 有最小值 4. 例2 关于抛物线 y = x2 + 1 与 y = x2 1,下列说法正确的是( ) A.开口方向相同 B.顶点相同 C.对称轴相同 D.当 x>0 时,y 随 x 的增大而增大 师生活动:教师给出例题后,让学生独立作业,同时分别选派四名同学上黑板演算. 教师巡视,对学生演算过程中的失误及时予以指正,最后师生共同评析。 知识点2: 二次函数 y = ax2 + k (a≠0) 的图象及平移 做一做:填写下表,画出二次函数 y = 2x , y = 2x2 + 1 ,y = 2x2 1的图象. 观察上述图象,说说它们之间的区别与联系. 想一想 1. 抛物线 y = ax2 + k (a≠0) 与抛物线 y = ax2 有什么关系? 上下平移规律: 二次项不变,常数项上加下减. 链接中考 1. 将二次函数 y = -2x2﹣2 的图象向上平移 3 个单位长度,得到的图象所对应的函数解析式是 . 预设:y = -2x2 + 1 想一想 抛物线 y = ax2 + k (a≠0) 中的 a 决定什么?k 决定什么?它的对称轴是什么?顶点坐标怎样表示? 预设:a 决定开口方向和大小,k 决定顶点的纵坐标;对称轴为 y 轴;顶点坐标为 (0,k). 三、当堂练习,巩固所学 1. 填表: 2. 已知 (m,n) 在 y = ax2 + a (a≠0) 的图象上,则点 ( m,n) ____ (填“在”或“不在”) y = ax2 + a (a≠0) 的图象上. 3. 已知抛物线 y = (a 2)x2 + a2 2 的最高点为 (0,2),则 a =____. 设计意图:类比一次函数,通过平移正比例函数可以得到一般函数,引导学生思考二次函数y=ax2通过平移可以得到哪些函数. 设计意图:类比研究二次函数y=ax2 的方法,从解析式,描点法和图象法三个维度分析二次函数 y = ax2 + k 的图象和性质. 设计意图:让学生思考和交流对函数性质的认识,并积累从图象的角度研究 函数性质的经验. 设计意图:经历从特殊到一般的研究过程,归纳出二次函数y= =ax2+k (a>0) 的图象特征和性质. 设计意图:引导学生类比 研究a>0 时二次函数的方法,归纳当a< 0时二次函数y = ax2 + k的图象特征和性质. 设计意图:加强学生对二次函数y = ax2 + k的图象特征和性质的理解. 设计意图:从数的角度和形的角度读探讨平移之间的关系,让学生学会数形结合的思想,同时经历从特殊到一般的研究过程,得出二次函数y=ax2+k与y=ax2的图象关系. 设计意图:加强学生对二次函数y = ax2 + k的平移性质的理解. 设计意图:帮助学生总结二次函数与系数之间的关系. 设计意图:考查学生对二次函数的性质的掌握. 及时练习巩固,体现学以致用的观念,消除学生学无所用的思想顾虑。
板书设计 第1课时 二次函数 y = ax2 + k 的图象和性质 1.二次函数y=ax2+k的图象与性质: 2.二次函数y=ax2和y=ax2+k的应用.
课后小结 教师与学生一起回顾本节课所学的主要内容,梳理并完善知识思维导图。
教学反思 尝试用描点法画二次函数y=ax2 + k图象,利用多媒体生动形象引导学生总结归纳二次函数y=ax2 + k的性质。内容较为简单,在教学中应鼓励学生积极思考,归纳总结,允许学生回答的不完整,甚至有错误的见解,培养学生乐于分享、发言的习惯,提高学生学习数学的兴趣。
同课章节目录
