22.1.3 第3课时 二次函数y=a(x-h)² k的图象和性质 教案(表格式)2025-2026学年度人教版数学九年级上册
文档属性
| 名称 | 22.1.3 第3课时 二次函数y=a(x-h)² k的图象和性质 教案(表格式)2025-2026学年度人教版数学九年级上册 |  | |
| 格式 | docx | ||
| 文件大小 | 3.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-22 11:21:01 | ||
图片预览



文档简介
九年级上册教案
22.1.3 二次函数 y = a(x h)2 + k 的
图象和性质
第3课时 二次函数 y = a(x h)2 + k 的图象和性质
教学内容 第3课时 二次函数 y = a(x h)2 + k 的图象和性质 课时 1
核心素养目标 1.引导学生运用观察、分析、比较、抽象、类比、概况等方法,探究二次函数y=a(x-h)2+k的图象和它的开口方向、对称轴、顶点坐标及增减性等; 2.掌握二次函数y=a(x-h)2+k的图象的平移规律; 3.向学生渗透事物总是不断运动变化和发展的观点,进一步培养学生数形结合的思想、动手操作能力和逻辑思维能力.
知识目标 1.掌握二次函数y=ax2与y=a(x-h)2+k(a≠0)图象之间的联系; 2.能灵活运用二次函数y=a(x-h)2+k(a≠0)的知识解决简单的问题.
教学重点 掌握二次函数y=ax2与y=a(x-h)2+k(a≠0)图象之间的联系.
教学难点 能灵活运用二次函数y=a(x-h)2+k(a≠0)的知识解决简单的问题.
教学准备 课件
教学过程 主要师生活动 设计意图
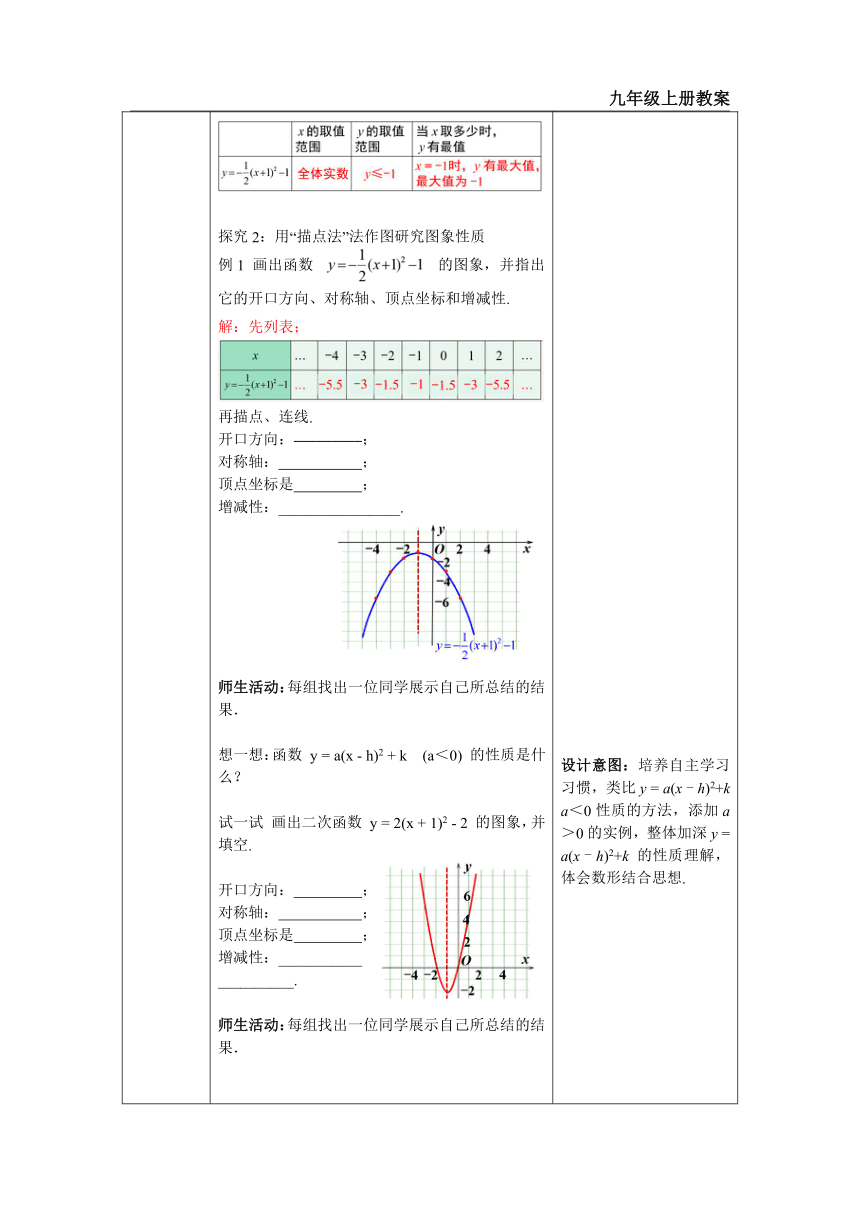
一、情境导入 二、探究新知 当堂练习,巩固所学 一、创设情境,导入新知 1. 抛物线 y = ax2 经过怎样的移动可以得到抛物线y = a(x - h)2,y = ax2 + k? 师生活动:让学生自主回答. (学生积极踊跃发言,问答提出的问题.) 二、小组合作,探究概念和性质 知识点1: 二次函数 y=a(x - h)2 + k 的图象和性质 操作与思考:画出二次函数 的图象. 师生活动:学生自主列表画图,然后小组讨论问题 探究1:从函数解析式研究图象和性质. 探究2:用“描点法”法作图研究图象性质 例1 画出函数 的图象,并指出它的开口方向、对称轴、顶点坐标和增减性. 解:先列表; 再描点、连线. 开口方向: ; 对称轴: ; 顶点坐标是 ; 增减性:________________. 师生活动:每组找出一位同学展示自己所总结的结果. 想一想:函数 y = a(x - h)2 + k (a<0) 的性质是什么? 试一试 画出二次函数 y = 2(x + 1)2 - 2 的图象,并填空. 开口方向: ; 对称轴: ; 顶点坐标是 ; 增减性:___________ __________. 师生活动:每组找出一位同学展示自己所总结的结果. 想一想:函数 y = a(x - h)2 + k (a>0) 的性质是什么? 归纳总结 师生活动:学生举手回答问题,出现错误及时解释指正. 典例精析 例2 已知抛物线 y=a(x 3)2 + 2 经过点 (1, 2). (1) 指出抛物线的对称轴; (2) 求 a 的值. (3) 若点 A(m,y1)、B(n,y2) (m<n<3) 都在该抛物线上,试比较 y1 与 y2 的大小. 师生活动: 1.两名学生板演,其余学生在练习本上做题; 2小组内批阅; 3.对板演的内容进行评价纠错. 解:(1) 由 y=a(x﹣3)2 + 2 可知其顶点为 (3,2), 对称轴为直线 x=3. (2) ∵ 抛物线 y=a(x﹣3)2 + 2 经过点(1,-2), ∴ -2=a(1 - 3)2 + 2, ∴ a=-1. (3) ∵ y=﹣(x﹣3)2 + 2, ∴ 此函数的图象开口向下, 当 x<3 时,y 随 x 的增大而增大. ∵ 点 A(m,y1),B(n,y2) (m<n<3) 都在该抛物线上, ∴ y1<y2. 知识点2 二次函数 y=a(x + h)2+k 与 y=ax2(a≠0) 的关系 画一画,填出下表: 师生活动:学生用描点法画出二次函数的图象,然后同组的同学比较所画的图象是否一样,根据自己所画出的函数图象,指出其开口方向、对称轴和顶点坐标,并观察其增减性. 师生活动:老师播放PPT,让学生观察,然后小组谈论,探讨平移的方法. 归纳总结 二次函数 y = ax2 与 y = a(x±h)2±k 的关系 平移规律(设 h>0,k>0): 简记为: 上下平移,常数项上加下减; 左右平移,自变量左加右减. 二次项系数 a 不变. 师生活动:让学生尝试解答,并互相交流、总结,归纳解题步骤,教师结合学生的具体活动,加以指导. 链接中考 1. (哈尔滨)将抛物线 y =﹣5x2 + 1 向左平移 1 个单位长度,再向下平移 2 个单位长度,所得到的抛物线为 ( ) A.y =﹣5(x + 1)2﹣1 B.y =﹣5(x﹣1)2﹣1 C.y =﹣5(x + 1)2 + 3 D.y =﹣5(x﹣1)2 + 3 想一想 问题 一次函数 y = kx + b 的图象如下图所示,请根据一次函数图象的性质填空: 试着画出二次函数 y = a(x - h)2 + k 不同情况下的大致图象. ( 按 a,h,k 的正负分类 ) 例4 已知二次函数 y=a(x-1)2-k 的图象如图所示,则一次函数 y=ax+k 的大致图象是 ( ) 师生活动:让学生尝试解答,举手回答问题. 归纳总结 说一说,对于二次函数 y = a(x - h)2 + k (a≠0) 图象性质中,字母 a,h,k 所起的作用. 结论:① a 决定开口方向. ② (h,k) 决定顶点坐标. h 决定对称轴 (直线 x = h). h<0, 对称轴在 y 轴的左侧; h>0,对称轴在 y 轴的右侧; k>0,顶点在 x 轴的上侧; k<0,顶点在 x 轴的下侧. ③ a,h(对称轴) 决定函数的增减性. 例5 要修建一个圆形喷水池,在池中心竖直安装一根水管.在水管的顶端安装一个喷水头,使喷出的抛物线形水柱在与池中心的水平距离为 1 m 处达到最高,高度为 3 m,水柱落地处离池中心 3 m,水管应多长 三、当堂练习,巩固所学 1. 完成下列表格: 2. 已知函数 y=﹣(x﹣4)2﹣1. (1) 指出函数图象的开口方向是 ,对称轴是 ,顶点坐标为 ; (2) 当 x 时,y 随 x 的增大而减小; (3) 怎样移动抛物线 y=﹣x2,就可以得到抛物线 y=﹣(x﹣4)2﹣1 3. 已知二次函数 y=a(x-1)2-4 的图象经过点 (3,0). (1) 求 a 的值; (2) 若 A(m,y1)、B(m+n,y2) (n>0) 是该函数图象上的两点,当 y1=y2 时,求 m、n 之间的数量关系. 设计意图:让学生在温习旧知识的过程中体验会旧知与新知之间的联系,活动思维,为后面的学习做准备. 设计意图:培养自主学习习惯,类比y = a(x - h)2+k a<0性质的方法,添加a>0的实例,整体加深y = a(x - h)2+k 的性质理解,体会数形结合思想. 设计意图:培养学生归纳、整理知识的意识.注意将图象与表达式进行联系, 让学生理解知识点. 设计意图:通过数形结合,加强学生对二次函数性质的理解. 设计意图: 经过前期的探索,学生完全有能力推测出解析式的变化会引起图象的何种变化. 因此,先让学生合情推理,再画图验证,培养学生的合情推理能力和分析能力,有利于培养学生的数学直觉和感悟能力.利用图象,直观地研究二次函数的性质,可以培养学生用数形结合的方法思考,积累研究函数性质的经验.最后,总结规律,有效地让学生从感性认识上升到了理性认识,并形成自己对本节课重点内容的理解. 设计意图:巩固二次函数平移的方法,加强对其的理解. 设计意图:回顾一次函数的系数与图象之间的联系,为下面研究二次函数系数与图象之间的关系做铺垫. 设计意图:通过画图初步感受 a,h,k 的正负对图象的影响. 设计意图:巩固学生从二次函数图象中辨别系数的正负的方法. 设计意图:总结 a,h,k 的正负对图象的影响. 设计意图:同时引入实际问题,使学生感受二次函数在实际问题中的应用,学会建立基本数学模型,体会数学来源于生活,又反过来服务于生活。 设计意图:考查学生对二次函数的性质和平移的掌握. 及时练习巩固,体现学以致用的观念,消除学生学无所用的思想顾虑。
板书设计 二次函数y=a(x-h)2+k的图象与性质 1.二次函数y=a(x-h)2+k的图象与性质 2.二次函数y=a(x-h)2+k的图象与y=ax2的图象的关系 3.二次函数y=a(x-h)2+k的应用
课后小结 教师与学生一起回顾本节课所学的主要内容,梳理并完善知识思维导图。 一般地,抛物线 y = a( x - h )2 + k (a≠0) 与 y = ax2 (a≠0) 的形状相同,位置不同.
教学反思 要使课堂真正成为学生展示自我的舞台,还学生课堂学习的主体地位,教师要把激发学生学习热情和提高学生学习能力放在教学首位,为学生提供展示自己聪明才智的机会,使课堂真正成为学生展示自我的舞台.充分利用合作交流的形式,能使教师发现学生分析问题、解决问题的独到见解以及思维的误区,以便指导今后的教学.
22.1.3 二次函数 y = a(x h)2 + k 的
图象和性质
第3课时 二次函数 y = a(x h)2 + k 的图象和性质
教学内容 第3课时 二次函数 y = a(x h)2 + k 的图象和性质 课时 1
核心素养目标 1.引导学生运用观察、分析、比较、抽象、类比、概况等方法,探究二次函数y=a(x-h)2+k的图象和它的开口方向、对称轴、顶点坐标及增减性等; 2.掌握二次函数y=a(x-h)2+k的图象的平移规律; 3.向学生渗透事物总是不断运动变化和发展的观点,进一步培养学生数形结合的思想、动手操作能力和逻辑思维能力.
知识目标 1.掌握二次函数y=ax2与y=a(x-h)2+k(a≠0)图象之间的联系; 2.能灵活运用二次函数y=a(x-h)2+k(a≠0)的知识解决简单的问题.
教学重点 掌握二次函数y=ax2与y=a(x-h)2+k(a≠0)图象之间的联系.
教学难点 能灵活运用二次函数y=a(x-h)2+k(a≠0)的知识解决简单的问题.
教学准备 课件
教学过程 主要师生活动 设计意图
一、情境导入 二、探究新知 当堂练习,巩固所学 一、创设情境,导入新知 1. 抛物线 y = ax2 经过怎样的移动可以得到抛物线y = a(x - h)2,y = ax2 + k? 师生活动:让学生自主回答. (学生积极踊跃发言,问答提出的问题.) 二、小组合作,探究概念和性质 知识点1: 二次函数 y=a(x - h)2 + k 的图象和性质 操作与思考:画出二次函数 的图象. 师生活动:学生自主列表画图,然后小组讨论问题 探究1:从函数解析式研究图象和性质. 探究2:用“描点法”法作图研究图象性质 例1 画出函数 的图象,并指出它的开口方向、对称轴、顶点坐标和增减性. 解:先列表; 再描点、连线. 开口方向: ; 对称轴: ; 顶点坐标是 ; 增减性:________________. 师生活动:每组找出一位同学展示自己所总结的结果. 想一想:函数 y = a(x - h)2 + k (a<0) 的性质是什么? 试一试 画出二次函数 y = 2(x + 1)2 - 2 的图象,并填空. 开口方向: ; 对称轴: ; 顶点坐标是 ; 增减性:___________ __________. 师生活动:每组找出一位同学展示自己所总结的结果. 想一想:函数 y = a(x - h)2 + k (a>0) 的性质是什么? 归纳总结 师生活动:学生举手回答问题,出现错误及时解释指正. 典例精析 例2 已知抛物线 y=a(x 3)2 + 2 经过点 (1, 2). (1) 指出抛物线的对称轴; (2) 求 a 的值. (3) 若点 A(m,y1)、B(n,y2) (m<n<3) 都在该抛物线上,试比较 y1 与 y2 的大小. 师生活动: 1.两名学生板演,其余学生在练习本上做题; 2小组内批阅; 3.对板演的内容进行评价纠错. 解:(1) 由 y=a(x﹣3)2 + 2 可知其顶点为 (3,2), 对称轴为直线 x=3. (2) ∵ 抛物线 y=a(x﹣3)2 + 2 经过点(1,-2), ∴ -2=a(1 - 3)2 + 2, ∴ a=-1. (3) ∵ y=﹣(x﹣3)2 + 2, ∴ 此函数的图象开口向下, 当 x<3 时,y 随 x 的增大而增大. ∵ 点 A(m,y1),B(n,y2) (m<n<3) 都在该抛物线上, ∴ y1<y2. 知识点2 二次函数 y=a(x + h)2+k 与 y=ax2(a≠0) 的关系 画一画,填出下表: 师生活动:学生用描点法画出二次函数的图象,然后同组的同学比较所画的图象是否一样,根据自己所画出的函数图象,指出其开口方向、对称轴和顶点坐标,并观察其增减性. 师生活动:老师播放PPT,让学生观察,然后小组谈论,探讨平移的方法. 归纳总结 二次函数 y = ax2 与 y = a(x±h)2±k 的关系 平移规律(设 h>0,k>0): 简记为: 上下平移,常数项上加下减; 左右平移,自变量左加右减. 二次项系数 a 不变. 师生活动:让学生尝试解答,并互相交流、总结,归纳解题步骤,教师结合学生的具体活动,加以指导. 链接中考 1. (哈尔滨)将抛物线 y =﹣5x2 + 1 向左平移 1 个单位长度,再向下平移 2 个单位长度,所得到的抛物线为 ( ) A.y =﹣5(x + 1)2﹣1 B.y =﹣5(x﹣1)2﹣1 C.y =﹣5(x + 1)2 + 3 D.y =﹣5(x﹣1)2 + 3 想一想 问题 一次函数 y = kx + b 的图象如下图所示,请根据一次函数图象的性质填空: 试着画出二次函数 y = a(x - h)2 + k 不同情况下的大致图象. ( 按 a,h,k 的正负分类 ) 例4 已知二次函数 y=a(x-1)2-k 的图象如图所示,则一次函数 y=ax+k 的大致图象是 ( ) 师生活动:让学生尝试解答,举手回答问题. 归纳总结 说一说,对于二次函数 y = a(x - h)2 + k (a≠0) 图象性质中,字母 a,h,k 所起的作用. 结论:① a 决定开口方向. ② (h,k) 决定顶点坐标. h 决定对称轴 (直线 x = h). h<0, 对称轴在 y 轴的左侧; h>0,对称轴在 y 轴的右侧; k>0,顶点在 x 轴的上侧; k<0,顶点在 x 轴的下侧. ③ a,h(对称轴) 决定函数的增减性. 例5 要修建一个圆形喷水池,在池中心竖直安装一根水管.在水管的顶端安装一个喷水头,使喷出的抛物线形水柱在与池中心的水平距离为 1 m 处达到最高,高度为 3 m,水柱落地处离池中心 3 m,水管应多长 三、当堂练习,巩固所学 1. 完成下列表格: 2. 已知函数 y=﹣(x﹣4)2﹣1. (1) 指出函数图象的开口方向是 ,对称轴是 ,顶点坐标为 ; (2) 当 x 时,y 随 x 的增大而减小; (3) 怎样移动抛物线 y=﹣x2,就可以得到抛物线 y=﹣(x﹣4)2﹣1 3. 已知二次函数 y=a(x-1)2-4 的图象经过点 (3,0). (1) 求 a 的值; (2) 若 A(m,y1)、B(m+n,y2) (n>0) 是该函数图象上的两点,当 y1=y2 时,求 m、n 之间的数量关系. 设计意图:让学生在温习旧知识的过程中体验会旧知与新知之间的联系,活动思维,为后面的学习做准备. 设计意图:培养自主学习习惯,类比y = a(x - h)2+k a<0性质的方法,添加a>0的实例,整体加深y = a(x - h)2+k 的性质理解,体会数形结合思想. 设计意图:培养学生归纳、整理知识的意识.注意将图象与表达式进行联系, 让学生理解知识点. 设计意图:通过数形结合,加强学生对二次函数性质的理解. 设计意图: 经过前期的探索,学生完全有能力推测出解析式的变化会引起图象的何种变化. 因此,先让学生合情推理,再画图验证,培养学生的合情推理能力和分析能力,有利于培养学生的数学直觉和感悟能力.利用图象,直观地研究二次函数的性质,可以培养学生用数形结合的方法思考,积累研究函数性质的经验.最后,总结规律,有效地让学生从感性认识上升到了理性认识,并形成自己对本节课重点内容的理解. 设计意图:巩固二次函数平移的方法,加强对其的理解. 设计意图:回顾一次函数的系数与图象之间的联系,为下面研究二次函数系数与图象之间的关系做铺垫. 设计意图:通过画图初步感受 a,h,k 的正负对图象的影响. 设计意图:巩固学生从二次函数图象中辨别系数的正负的方法. 设计意图:总结 a,h,k 的正负对图象的影响. 设计意图:同时引入实际问题,使学生感受二次函数在实际问题中的应用,学会建立基本数学模型,体会数学来源于生活,又反过来服务于生活。 设计意图:考查学生对二次函数的性质和平移的掌握. 及时练习巩固,体现学以致用的观念,消除学生学无所用的思想顾虑。
板书设计 二次函数y=a(x-h)2+k的图象与性质 1.二次函数y=a(x-h)2+k的图象与性质 2.二次函数y=a(x-h)2+k的图象与y=ax2的图象的关系 3.二次函数y=a(x-h)2+k的应用
课后小结 教师与学生一起回顾本节课所学的主要内容,梳理并完善知识思维导图。 一般地,抛物线 y = a( x - h )2 + k (a≠0) 与 y = ax2 (a≠0) 的形状相同,位置不同.
教学反思 要使课堂真正成为学生展示自我的舞台,还学生课堂学习的主体地位,教师要把激发学生学习热情和提高学生学习能力放在教学首位,为学生提供展示自己聪明才智的机会,使课堂真正成为学生展示自我的舞台.充分利用合作交流的形式,能使教师发现学生分析问题、解决问题的独到见解以及思维的误区,以便指导今后的教学.
同课章节目录
