22.2 二次函数与一元二次方程 教案(表格式)2025-2026学年度人教版数学九年级上册
文档属性
| 名称 | 22.2 二次函数与一元二次方程 教案(表格式)2025-2026学年度人教版数学九年级上册 |  | |
| 格式 | docx | ||
| 文件大小 | 2.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-22 11:54:56 | ||
图片预览



文档简介
九年级上册教案
22.2 二次函数与一元二次方程
教学内容 22.2 二次函数与一元二次方程 课时 1
核心素养目标 1.体会函数与方程之间的联系,初步体会利用函数图象研究方程问题的方法. 2.理解二次函数图象与x轴交点的个数与一元二次方程的根的个数之间的关系,理解方程有两个不等的实根、两个相等的实根和没有实根的函数图象特征. 3.经历类比、观察、发现、归纳的探索过程,体会函数与方程相互转化的数学思想和数形结合的数学思想. 4.利用图象法求一元二次方程的近似根,重要的是让学生懂得这种求解方法的思路,体验数形结合思想.
知识目标 1.通过探索,理解二次函数与一元二次方程之间的联系. 2.能运用二次函数及其图象确定方程和不等式的解或解集. 3.根据函数图象与x轴的交点情况确定未知字母的值或取值范围.
教学重点 能运用二次函数及其图象确定方程和不等式的解或解集
教学难点 根据函数图象与x轴的交点情况确定未知字母的值或取值范围
教学准备 课件
教学过程 主要师生活动 设计意图
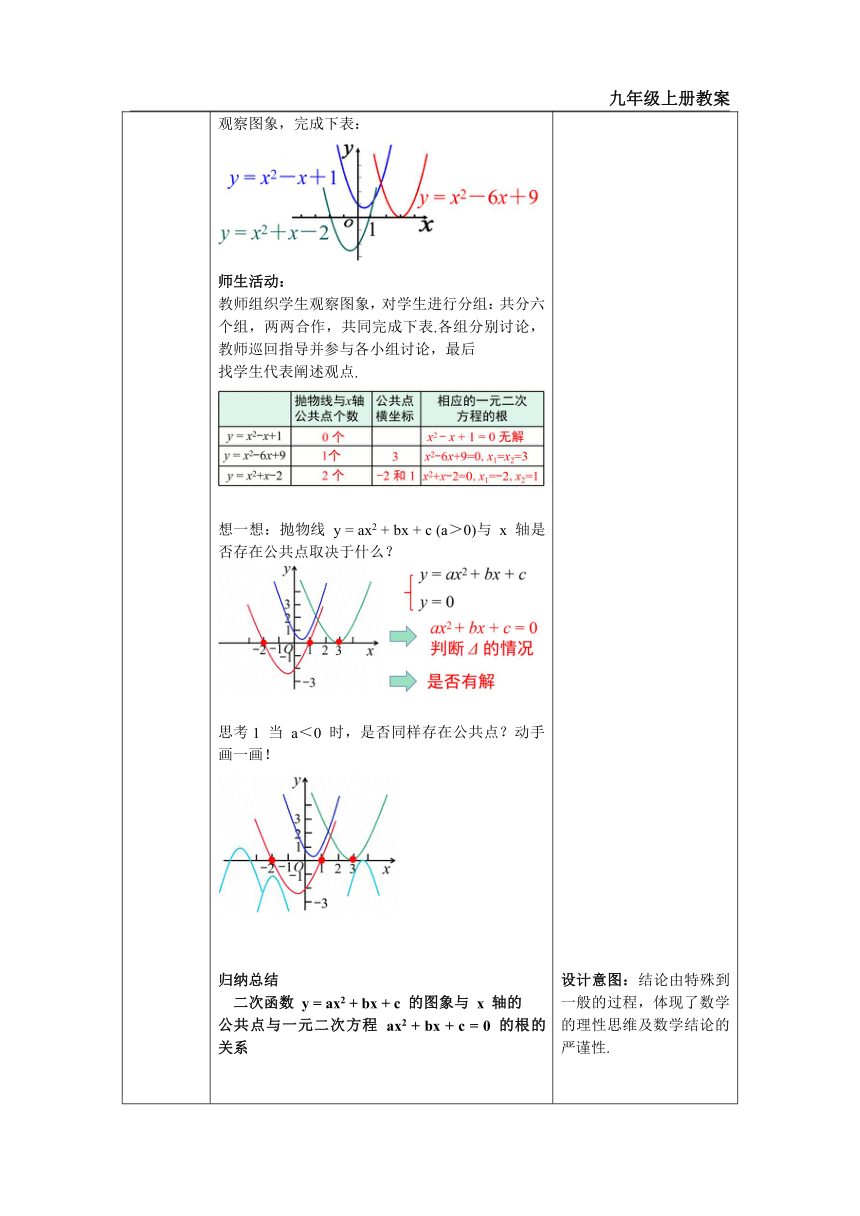
一、情境导入 二、探究新知 当堂练习,巩固所学 一、创设情境,导入新知 思考 一次函数,二次函数都是由无数个点组成,那么最重要的是哪几种点呢? 预设:与 x 轴、y 轴的交点. 追问1:怎么求与 x 轴的交点? 追问2:那么二次函数呢? 师生活动:让学生自主回答. (学生积极踊跃发言,问答提出的问题.) 二、小组合作,探究概念和性质 知识点1: 二次函数与一元二次方程的关系 如图,以 40 m/s 的速度将小球沿与地面成 30° 角的方向击出时,小球的飞行路线将是一条抛物线,如果不考虑空气的阻力,小球的飞行高度 h(单位:m)与飞行时间 t(单位:s)之间具有函数关系h = 20t - 5t2. 考虑以下问题: 小球的飞行高度能否达到 15 m?如果能,需要多少飞行时间? 师生活动: 要求学生先独立解决,然后同伴交流,相互订正,代表展示成果. 教师及时指导. 分析:① 建立平面直角坐标系 ② 小球的飞行高度能否达到 15 m → 当 h = 15 时,自变量 t 的取值. 解:令 15 = 20t - 5t2, 即 t2 - 4t + 3 = 0, 解得 t1 = 1,t2 = 3. 故当小球飞行 1 s 或 3 s 时, 它的高度为 15 m. 你能结合上图,指出为什么在两个时间小球的高度为 15 m 吗? 小球的飞行高度能否达到 20 m?如果能,需要多少飞行时间? 解:令 20 = 20t - 5t2, 即 t2 - 4t + 4 = 0, 解得 t1 = t2 = 2. 故当球飞行 2 s 时,它的高度为 20 m. 你能结合图形指出为什么只在一个时间小球的高度为 20 m 吗? 小球从飞出到落地要用多少时间? 解:小球飞出时和落地时的高度都为 0 m, 令 0 = 20t - 5t2, 即 t2 - 4t = 0, 解得 t1 = 0,t2 = 4. 故当小球飞行 0 s 和 4 s 时,它的高度为 0 m. ∴ 小球从飞出到落地要用 4 s 时间. 从上面发现,二次函数 y = ax2 + bx + c 何时为一元二次方程 一般地,当 y 取确定值且 a≠0 时,二次函数为一元二次方程. 如:y = 5 时,则 5 = ax2 + bx + c (a ≠ 0)就是一个一元二次方程. 归纳总结 二次函数与一元二次方程紧密地联系起来了. 知识点2: 利用二次函数深入讨论一元二次方程 合作探究 观察思考下列二次函数的图象与 x 轴有公共点吗?如果有,公共点的横坐标是多少?当 x 取公共点的横坐标时,函数的值是多少?由此你能得出相应的一元二次方程的根吗? (1) y = x2 - x + 1; (2) y = x2 - 6x + 9; (3) y = x2 + x - 2. 观察图象,完成下表: 师生活动: 教师组织学生观察图象,对学生进行分组:共分六个组,两两合作,共同完成下表.各组分别讨论,教师巡回指导并参与各小组讨论,最后 找学生代表阐述观点. 想一想:抛物线 y = ax2 + bx + c (a>0)与 x 轴是否存在公共点取决于什么? 思考1 当 a<0 时,是否同样存在公共点?动手画一画! 归纳总结 二次函数 y = ax2 + bx + c 的图象与 x 轴的 公共点与一元二次方程 ax2 + bx + c = 0 的根的关系 五点画图法 画出二次函数 y = x2 - 4x + 3 的图象 链接中考 1. (崂山区) 若二次函数 y = ax2 - 2x - 1 的图象和 x 轴有交点,则 a 的取值范围为________________. 预设:a≥-1 且 a≠0 总结 若抛物线 y = ax2 + bx + c 与 x 轴有交点, 则 b2 - 4ac≥0. 知识点3:利用二次函数的图象求一元二次方程的近似解 例1 利用函数图象求方程 x2 2x 2 = 0 的实数根(结果保留小数点后一位). 分析:一元二次方程 x 2x 2 = 0 的根就是抛物线 y = x 2x 2 与 x 轴的公共点的横坐标,因此我们可以先画出这条抛物线,然后从图上找出它与 x 轴的交点的横坐标,这种解一元二次方程的方法叫做图象法. 解:画出函数 y = x 2x 2 的图象(如下图),则方程有两个实数根,一个在 1 与 0 之间,另一个在 2 与 3 之间. 通过取平均数的方法不断缩小根的范围. 所以跟在 2.5 和 2.75 之间,然后重复上述步骤. 最终,根在 2.687 5 和 2.75 之间,要求精确到 0.1. 故取 x1≈2.7. 同理可得另一近似根为 x2≈-0.7. 练一练 1. 已知二次函数 y=ax2+bx+c 的图象如图所示,则一元二次方程 ax2+bx+c=0 的近似根为 ( ) A. x1≈-2.1,x2≈0.1 B. x1≈-2.5,x2≈0.5 C. x1≈-2.9,x2≈0.9 D.x1≈-3, x2≈1 师生活动:学生举手回答问题,对于有问题的加以分析. 三、当堂练习,巩固所学 1. 若一元二次方程 x2 - mx + n = 0 无实根,则抛物线 y = x2 - mx + n 图象位于( ) A. x 轴上方 B. 第一、二、三象限 C. x 轴下方 D. 第二、三、四象限 一元二次方程 3x2 + x -10 = 0 的两个根是 x1 = -2,x2 = ,那么二次函数 y = 3x2 + x - 10 与 x 轴的交点坐标是 . 3. 根据下列表格的对应值: 可知方程 ax2 + bx + c = 0 (a ≠ 0,a,b,c 为常数) 的一个解 x1 的范围是( ) A.3 < x1< 3.23 B. 3.23 < x1 < 3.24 C. 3.24 < x1 < 3.25 D. 3.25 < x1 < 3.26 4. 已知函数 y=(k-3)x2+2x+1 的图象与 x 轴有公共点,求 k 的取值范围. 5. 某学校初三年级的一场篮球比赛中,如图,队员甲正在投篮,已知球出手时距地面 m,与篮框中心的水平距离为 7 m,当球出手后水平距离为 4 m时到达最大高度 4 m,设篮球运行轨迹为抛物线,篮框距地面 3 m. (1) 建立如图所示的平面直角坐标系,问此球能否准确投中? (2) 此时,如果对方队员乙在甲面前 1 m 处跳起盖帽拦截,已知乙的最大摸高为 3.1 m,那么他能否获得成功? 设计意图:通过回忆一次函数求解与x轴的交点的方法,为二次函数求解与x轴交点的方法做铺垫. 同时让学生体会数形结合的思想,感知体会到二次函数和一元二次方程之间的联系. 设计意图:本环节以实际问题引入,在建立数学模型解决问题的过程中,让学生体会学科间的联系及数学建模思想,渗透了数学核心素养中的数学建模,同时初步感受二次函数和一元二次方程之间的联系. 设计意图:通过对三个函数图象与x轴交点的观察、对一元二次方程根 的求解,让学生进一步掌握二次函数与一元二次方程之间的关系,提高发现 问题、解决问题的能力. 设计意图:结论由特殊到一般的过程,体现了数学的理性思维及数学结论的严谨性. 设计意图:本环节的目的就是为了及时对新知进行巩固练习,检测学生对知识理解情况,同时在练习的过程中让学生再次体会二次函数的图象与一元二次方程的根之间的联系及如何运用这些知识解决数学问题. 设计意图:本环节一是让学生巩固对二次函数图象的形成的认识,二是让他们运用二次函数图象与x轴交点的横坐标就是方程ax2+bx+c=0的根的原理,经历一元二次方程根的近似值的探索过程,进一步体会二次函数与方程之间的联系. 设计意图:利用二次函数与一元二次方程的联系,根据函数图象求方程的近似解,进一步巩固所学内容. 设计意图:考查学生对二次函数与一元二次方程的联系的掌握
板书设计 22.2 二次函数与一元二次方程 1.二次函数与一元二次方程 2.利用二次函数解决运动中的抛物线问题
课后小结 教师与学生一起回顾本节课所学的主要内容,梳理并完善知识思维导图。
教学反思 本节课注意发挥学生的主体作用,让学生通过自主探究、合作学习来主动发现问题、提出问题、解决问题,实现师生互动,通过这样的教学实践取得一定的教学效果,再次认识到教师不仅要教给学生知识,更要培养学生良好的数学素养和学习习惯,让学生学会学习,使他们能够在独立思考与合作学习交流中解决学习中的问题.
22.2 二次函数与一元二次方程
教学内容 22.2 二次函数与一元二次方程 课时 1
核心素养目标 1.体会函数与方程之间的联系,初步体会利用函数图象研究方程问题的方法. 2.理解二次函数图象与x轴交点的个数与一元二次方程的根的个数之间的关系,理解方程有两个不等的实根、两个相等的实根和没有实根的函数图象特征. 3.经历类比、观察、发现、归纳的探索过程,体会函数与方程相互转化的数学思想和数形结合的数学思想. 4.利用图象法求一元二次方程的近似根,重要的是让学生懂得这种求解方法的思路,体验数形结合思想.
知识目标 1.通过探索,理解二次函数与一元二次方程之间的联系. 2.能运用二次函数及其图象确定方程和不等式的解或解集. 3.根据函数图象与x轴的交点情况确定未知字母的值或取值范围.
教学重点 能运用二次函数及其图象确定方程和不等式的解或解集
教学难点 根据函数图象与x轴的交点情况确定未知字母的值或取值范围
教学准备 课件
教学过程 主要师生活动 设计意图
一、情境导入 二、探究新知 当堂练习,巩固所学 一、创设情境,导入新知 思考 一次函数,二次函数都是由无数个点组成,那么最重要的是哪几种点呢? 预设:与 x 轴、y 轴的交点. 追问1:怎么求与 x 轴的交点? 追问2:那么二次函数呢? 师生活动:让学生自主回答. (学生积极踊跃发言,问答提出的问题.) 二、小组合作,探究概念和性质 知识点1: 二次函数与一元二次方程的关系 如图,以 40 m/s 的速度将小球沿与地面成 30° 角的方向击出时,小球的飞行路线将是一条抛物线,如果不考虑空气的阻力,小球的飞行高度 h(单位:m)与飞行时间 t(单位:s)之间具有函数关系h = 20t - 5t2. 考虑以下问题: 小球的飞行高度能否达到 15 m?如果能,需要多少飞行时间? 师生活动: 要求学生先独立解决,然后同伴交流,相互订正,代表展示成果. 教师及时指导. 分析:① 建立平面直角坐标系 ② 小球的飞行高度能否达到 15 m → 当 h = 15 时,自变量 t 的取值. 解:令 15 = 20t - 5t2, 即 t2 - 4t + 3 = 0, 解得 t1 = 1,t2 = 3. 故当小球飞行 1 s 或 3 s 时, 它的高度为 15 m. 你能结合上图,指出为什么在两个时间小球的高度为 15 m 吗? 小球的飞行高度能否达到 20 m?如果能,需要多少飞行时间? 解:令 20 = 20t - 5t2, 即 t2 - 4t + 4 = 0, 解得 t1 = t2 = 2. 故当球飞行 2 s 时,它的高度为 20 m. 你能结合图形指出为什么只在一个时间小球的高度为 20 m 吗? 小球从飞出到落地要用多少时间? 解:小球飞出时和落地时的高度都为 0 m, 令 0 = 20t - 5t2, 即 t2 - 4t = 0, 解得 t1 = 0,t2 = 4. 故当小球飞行 0 s 和 4 s 时,它的高度为 0 m. ∴ 小球从飞出到落地要用 4 s 时间. 从上面发现,二次函数 y = ax2 + bx + c 何时为一元二次方程 一般地,当 y 取确定值且 a≠0 时,二次函数为一元二次方程. 如:y = 5 时,则 5 = ax2 + bx + c (a ≠ 0)就是一个一元二次方程. 归纳总结 二次函数与一元二次方程紧密地联系起来了. 知识点2: 利用二次函数深入讨论一元二次方程 合作探究 观察思考下列二次函数的图象与 x 轴有公共点吗?如果有,公共点的横坐标是多少?当 x 取公共点的横坐标时,函数的值是多少?由此你能得出相应的一元二次方程的根吗? (1) y = x2 - x + 1; (2) y = x2 - 6x + 9; (3) y = x2 + x - 2. 观察图象,完成下表: 师生活动: 教师组织学生观察图象,对学生进行分组:共分六个组,两两合作,共同完成下表.各组分别讨论,教师巡回指导并参与各小组讨论,最后 找学生代表阐述观点. 想一想:抛物线 y = ax2 + bx + c (a>0)与 x 轴是否存在公共点取决于什么? 思考1 当 a<0 时,是否同样存在公共点?动手画一画! 归纳总结 二次函数 y = ax2 + bx + c 的图象与 x 轴的 公共点与一元二次方程 ax2 + bx + c = 0 的根的关系 五点画图法 画出二次函数 y = x2 - 4x + 3 的图象 链接中考 1. (崂山区) 若二次函数 y = ax2 - 2x - 1 的图象和 x 轴有交点,则 a 的取值范围为________________. 预设:a≥-1 且 a≠0 总结 若抛物线 y = ax2 + bx + c 与 x 轴有交点, 则 b2 - 4ac≥0. 知识点3:利用二次函数的图象求一元二次方程的近似解 例1 利用函数图象求方程 x2 2x 2 = 0 的实数根(结果保留小数点后一位). 分析:一元二次方程 x 2x 2 = 0 的根就是抛物线 y = x 2x 2 与 x 轴的公共点的横坐标,因此我们可以先画出这条抛物线,然后从图上找出它与 x 轴的交点的横坐标,这种解一元二次方程的方法叫做图象法. 解:画出函数 y = x 2x 2 的图象(如下图),则方程有两个实数根,一个在 1 与 0 之间,另一个在 2 与 3 之间. 通过取平均数的方法不断缩小根的范围. 所以跟在 2.5 和 2.75 之间,然后重复上述步骤. 最终,根在 2.687 5 和 2.75 之间,要求精确到 0.1. 故取 x1≈2.7. 同理可得另一近似根为 x2≈-0.7. 练一练 1. 已知二次函数 y=ax2+bx+c 的图象如图所示,则一元二次方程 ax2+bx+c=0 的近似根为 ( ) A. x1≈-2.1,x2≈0.1 B. x1≈-2.5,x2≈0.5 C. x1≈-2.9,x2≈0.9 D.x1≈-3, x2≈1 师生活动:学生举手回答问题,对于有问题的加以分析. 三、当堂练习,巩固所学 1. 若一元二次方程 x2 - mx + n = 0 无实根,则抛物线 y = x2 - mx + n 图象位于( ) A. x 轴上方 B. 第一、二、三象限 C. x 轴下方 D. 第二、三、四象限 一元二次方程 3x2 + x -10 = 0 的两个根是 x1 = -2,x2 = ,那么二次函数 y = 3x2 + x - 10 与 x 轴的交点坐标是 . 3. 根据下列表格的对应值: 可知方程 ax2 + bx + c = 0 (a ≠ 0,a,b,c 为常数) 的一个解 x1 的范围是( ) A.3 < x1< 3.23 B. 3.23 < x1 < 3.24 C. 3.24 < x1 < 3.25 D. 3.25 < x1 < 3.26 4. 已知函数 y=(k-3)x2+2x+1 的图象与 x 轴有公共点,求 k 的取值范围. 5. 某学校初三年级的一场篮球比赛中,如图,队员甲正在投篮,已知球出手时距地面 m,与篮框中心的水平距离为 7 m,当球出手后水平距离为 4 m时到达最大高度 4 m,设篮球运行轨迹为抛物线,篮框距地面 3 m. (1) 建立如图所示的平面直角坐标系,问此球能否准确投中? (2) 此时,如果对方队员乙在甲面前 1 m 处跳起盖帽拦截,已知乙的最大摸高为 3.1 m,那么他能否获得成功? 设计意图:通过回忆一次函数求解与x轴的交点的方法,为二次函数求解与x轴交点的方法做铺垫. 同时让学生体会数形结合的思想,感知体会到二次函数和一元二次方程之间的联系. 设计意图:本环节以实际问题引入,在建立数学模型解决问题的过程中,让学生体会学科间的联系及数学建模思想,渗透了数学核心素养中的数学建模,同时初步感受二次函数和一元二次方程之间的联系. 设计意图:通过对三个函数图象与x轴交点的观察、对一元二次方程根 的求解,让学生进一步掌握二次函数与一元二次方程之间的关系,提高发现 问题、解决问题的能力. 设计意图:结论由特殊到一般的过程,体现了数学的理性思维及数学结论的严谨性. 设计意图:本环节的目的就是为了及时对新知进行巩固练习,检测学生对知识理解情况,同时在练习的过程中让学生再次体会二次函数的图象与一元二次方程的根之间的联系及如何运用这些知识解决数学问题. 设计意图:本环节一是让学生巩固对二次函数图象的形成的认识,二是让他们运用二次函数图象与x轴交点的横坐标就是方程ax2+bx+c=0的根的原理,经历一元二次方程根的近似值的探索过程,进一步体会二次函数与方程之间的联系. 设计意图:利用二次函数与一元二次方程的联系,根据函数图象求方程的近似解,进一步巩固所学内容. 设计意图:考查学生对二次函数与一元二次方程的联系的掌握
板书设计 22.2 二次函数与一元二次方程 1.二次函数与一元二次方程 2.利用二次函数解决运动中的抛物线问题
课后小结 教师与学生一起回顾本节课所学的主要内容,梳理并完善知识思维导图。
教学反思 本节课注意发挥学生的主体作用,让学生通过自主探究、合作学习来主动发现问题、提出问题、解决问题,实现师生互动,通过这样的教学实践取得一定的教学效果,再次认识到教师不仅要教给学生知识,更要培养学生良好的数学素养和学习习惯,让学生学会学习,使他们能够在独立思考与合作学习交流中解决学习中的问题.
同课章节目录
