22.3 第1课时 几何图形的最大面积 教案(表格式)2025-2026学年度人教版数学九年级上册
文档属性
| 名称 | 22.3 第1课时 几何图形的最大面积 教案(表格式)2025-2026学年度人教版数学九年级上册 |  | |
| 格式 | docx | ||
| 文件大小 | 2.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-22 11:56:51 | ||
图片预览


文档简介
九年级上册教案
22.3 实际问题与二次函数
第1课时 几何图形的最大面积
教学内容 第1课时 几何图形的最大面积 课时 1
核心素养目标 1.能够分析和表示最大面积问题中变量之间的关系,并能运用二次函数求出最大值,增强解决问题的能力; 2.通过建立二次函数的数学模型解决实际问题,培养分析问题、解决问题的能力,提高用数学的意识,在解决问题的过程中体会数形结合思想.
知识目标 1.经历数学建模的基本过程,能分析实际问题中变量之间的二次函数关系; 2.会运用二次函数求实际问题中的最大值或最小值; 3.能应用二次函数的性质解决图形中最大面积问题.
教学重点 会运用二次函数求实际问题中的最大值或最小值
教学难点 能应用二次函数的性质解决图形中最大面积问题
教学准备 课件
教学过程 主要师生活动 设计意图
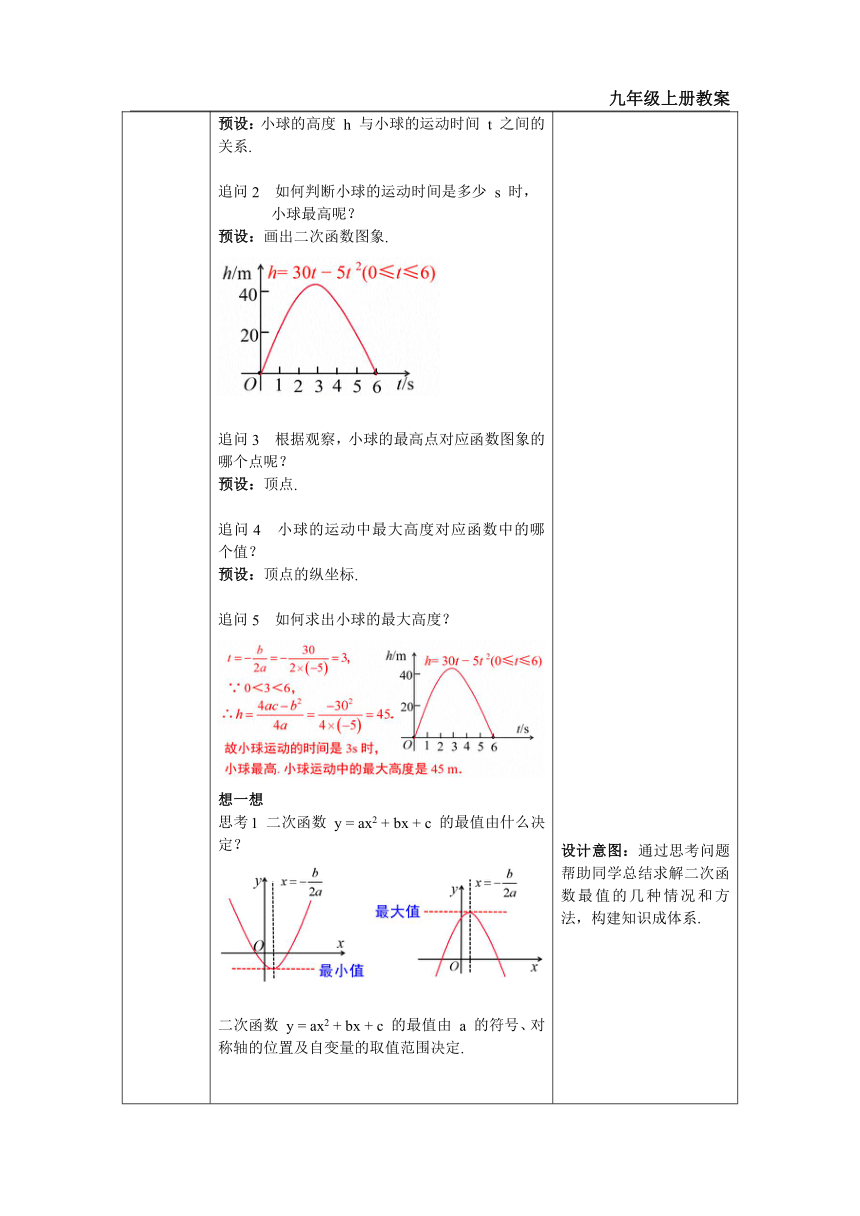
一、情境导入 二、探究新知 当堂练习,巩固所学 一、创设情境,导入新知 将一个物体抛向空中,时间与高度将成二次函数关系,那么你想知道该物体最多可以抛多高吗? 二、小组合作,探究概念和性质 知识点1: 求二次函数的最大(或最小)值 引例:从地面竖直向上抛出一小球,小球的高度 h (单位:m) 与小球的运动时间 t (单位:s)之间的关系式是 h = 30t - 5t2 (0≤t≤6). 小球的运动时间是多少 s 时,小球最高? 小球运动中的最大高度是多少? 追问1 这个问题研究的是哪两个变量之间的关系? 预设:小球的高度 h 与小球的运动时间 t 之间的关系. 追问2 如何判断小球的运动时间是多少 s 时, 小球最高呢? 预设:画出二次函数图象. 追问3 根据观察,小球的最高点对应函数图象的哪个点呢? 预设:顶点. 追问4 小球的运动中最大高度对应函数中的哪个值? 预设:顶点的纵坐标. 追问5 如何求出小球的最大高度? 想一想 思考1 二次函数 y = ax2 + bx + c 的最值由什么决定? 二次函数 y = ax2 + bx + c 的最值由 a 的符号、对称轴的位置及自变量的取值范围决定. 思考2 当自变量 x 为全体实数时,二次函数 y = ax2 + bx + c 的最值是多少? 思考3 当自变量 x 限定范围时,二次函数 y = ax2 + bx + c 的最值如何确定? 先判断 是否在限定范围内,若在,则二次函数在 x = 时取得一个最值,另一个最值需考察限定范围的端点处来决定;若不在,则根据二次函数的增减性确定其最值. 知识点2: 二次函数与几何图形面积的最值 例2 用总长为 60 m 的篱笆围成矩形场地,矩形面积 S (m2) 随矩形一边长 l (m) 的变化而变化. 当 l 是多少米时,场地的面积 S 最大? 思考 这个问题研究的是哪两个变量之间的关系? 预设:矩形面积 S 与一边长 l 的关系. 分析:则另一边长为__(30 l ) ___m. 矩形菜园的面积 S =__(30 l )l = l2 + 30l___. 问题 当 l 是多少米时,场地的面积 S 最大? 变式 如图,用一段长为 60 m 的篱笆围成一个一边靠墙的矩形菜园. (1) 当墙长 32 m 时,这个矩形的长、宽各为多少时,菜园的面积最大?最大面积是多少? 师生活动: 1.教师引导学生分析与矩形面积相关的量. 2.教师设问,如何用含x的代数式表示与其相邻的边的长度. 3.学生自主列函数解析式,并进行整理,讨论问题解答的正确性. 4.针对问题要求进行求解,并回答问题. 思考 这个问题研究的是哪两个变量之间的关系? 预设:矩形面积与一边长的关系. ① 设未知数,用含未知数的代数式表示相关量 解:设垂直于墙的一边长为 x m,则平行于墙的边长为 (60 2x) m. ∴ S = x(60 2x) = 2x2+60x . ② 根据题意,求出自变量的取值范围 ③ 写出二次函数解析式,并化为顶点式 ∵ S = 2x2+60x = 2(x 15)2 + 450, ④ 结合自变量的取值范围可知,该二次函数在其顶点处取得最大值 ∴ 当 x = 15 m 时,S 取最大值,此时 S最大值 = 450 m2. (2) 当墙长 18 m 时,这个矩形的长、宽各为多少时,菜园的面积最大?最大面积是多少? 想一想:当墙长发生改变时,根据问题(1),什么会发什么改变,什么不变? 解:设垂直于墙的一边长为 x m, 由 (1) 知 S = 2x2+60x = 2(x2 30x) = 2(x 15)2 + 450. ∴21≤x<30. ∵ 15<21, ∴ 当 21≤ x<30 时, S 随 x 的增大而减小, 故当 x = 21 时,S 取得最大值, 此时 S最大值= 2×(21 15)2 + 450 = 378 (m2). 归纳总结 二次函数解决几何面积最值问题的方法: 1. 求出函数解析式和自变量的取值范围; 2. 当自变量的取值范围没有限制时,可直接利用公式求它的最大值或最小值; 3. 当自变量的取值范围有所限制时,可先配成顶点式,然后画出函数图象的草图,再结合图象和自变量的范围求函数最值. 链接中考 1. (河北期末) 如图,嘉嘉欲借助院子里的一面长 15 m 的墙,想用长为 40 m 的网绳围成一个矩形 ABCD 给奶奶养鸡,怎样使矩形 ABCD 的面积最大呢 同学淇淇帮她解决了这个问题,淇淇的思路是:设 BC 的边长为 x m. 矩形 ABCD 的面积为 S m2 不考虑其他因素,请帮他们回答下列问题: (1) 求 S 与 x 的函数关系式. 直接写出 x 的取值范围; (2) x 为何值时,矩形 ABCD 的面积最大 师生活动: 1.两名学生板演,其余学生在练习本上做题。 2小组内批阅。 3.对板演的内容进行评价纠错。 三、当堂练习,巩固所学 1. 广场上喷水池中的喷头微露水面,喷出的水线呈一条抛物线,水线上水珠的高度 y 米关于水珠和喷头的水平距离 x 米的函数解析式是 (0≤x≤4),那么水珠的高度达到最大时,水珠与喷头的水平距离是( ) A. 1 米 B. 2 米 C. 5 米 D. 6 米 2. 已知直角三角形的两直角边之和为 8,则该三角形的面积的最大值是______. 3. 某小区要在一块空地上修建一个矩形绿化带 ABCD,绿化带一边靠墙 (墙长 25 m),另三边用总长为 40 m 的栅栏围住.设绿化带的边长 BD 为 x m,绿化带的面积为 y m2. (1) 求 y 与 x 之间的函数关系式,并写出自变量的取值范围. (2) 当 x 为何值时,满足条件的绿化带的面积最大? 设计意图: 创设现实生活问题情境,吸引学生兴趣,培养学生用数学眼光观察现实世界的意识. 设计意图:通过追问为学生提供解决此类问题的思路,让学生在问题解决的过程中体会二次函数与实际问题的联系,用二次函数的最大值等知识刻画实际问题中的最大高度. 设计意图:通过思考问题帮助同学总结求解二次函数最值的几种情况和方法,构建知识成体系. 设计意图:借助分析和问题,指导学生解决此类问题的基本过程和方法,使不同水平的学生有不同层次的发现,加深对本题数量关系的理解,这样会使学生对函数有一个更深层次的理解和认识,同时便于他们今后应用这一数学模型解决实际问题。 设计意图:根据墙长的变化,面积的表达式也在变化,同时自变量的取值范围也在变化;在求最值时,一定需要考虑自变量的取值是否在取值范围内,不在的时候根据函数草图结合自变量的范围求取最值. 设计意图:把数学问题变式到实际生活问题,让学生把数学知识运用到日常生活中,体会用数学的过程.由矩形面积变式到复合型面积,拓展了思维,以不变应万变,通过本题的训练让学生进一步体会利用二次函数解决最大面积问题的方法、过程. 设计意图: 针对本课时的主要问题,从多个角度、分层次进 行检测,达到学有所成、了解课堂学习效果的目的.
板书设计 22.3 实际问题与二次函数 第1课时 几何图形的最大面积 二次函数解决几何面积最值问题的方法: 1. 求出函数解析式和自变量的取值范围; 2. 当自变量的取值范围没有限制时,可直接利用公式 求它的最大值或最小值; 3. 当自变量的取值范围有所限制时,可先配成顶点式, 然后画出函数图象的草图,再结合图象和自变量的 范围求函数最值.
课后小结 教师与学生一起回顾本节课所学的主要内容,梳理并完善知识思维导图。
教学反思 由于本节课的内容是二次函数的应用问题,重在通过学习总结解决问题的方法,故而本节课以“启发探究式”为主线开展教学活动,以学生动手动脑探究为主,必要时加以小组合作讨论,充分调动学生学习积极性和主动性,突出学生的主体地位,达到“不但使学生学会,而且使学生会学”的目的.
22.3 实际问题与二次函数
第1课时 几何图形的最大面积
教学内容 第1课时 几何图形的最大面积 课时 1
核心素养目标 1.能够分析和表示最大面积问题中变量之间的关系,并能运用二次函数求出最大值,增强解决问题的能力; 2.通过建立二次函数的数学模型解决实际问题,培养分析问题、解决问题的能力,提高用数学的意识,在解决问题的过程中体会数形结合思想.
知识目标 1.经历数学建模的基本过程,能分析实际问题中变量之间的二次函数关系; 2.会运用二次函数求实际问题中的最大值或最小值; 3.能应用二次函数的性质解决图形中最大面积问题.
教学重点 会运用二次函数求实际问题中的最大值或最小值
教学难点 能应用二次函数的性质解决图形中最大面积问题
教学准备 课件
教学过程 主要师生活动 设计意图
一、情境导入 二、探究新知 当堂练习,巩固所学 一、创设情境,导入新知 将一个物体抛向空中,时间与高度将成二次函数关系,那么你想知道该物体最多可以抛多高吗? 二、小组合作,探究概念和性质 知识点1: 求二次函数的最大(或最小)值 引例:从地面竖直向上抛出一小球,小球的高度 h (单位:m) 与小球的运动时间 t (单位:s)之间的关系式是 h = 30t - 5t2 (0≤t≤6). 小球的运动时间是多少 s 时,小球最高? 小球运动中的最大高度是多少? 追问1 这个问题研究的是哪两个变量之间的关系? 预设:小球的高度 h 与小球的运动时间 t 之间的关系. 追问2 如何判断小球的运动时间是多少 s 时, 小球最高呢? 预设:画出二次函数图象. 追问3 根据观察,小球的最高点对应函数图象的哪个点呢? 预设:顶点. 追问4 小球的运动中最大高度对应函数中的哪个值? 预设:顶点的纵坐标. 追问5 如何求出小球的最大高度? 想一想 思考1 二次函数 y = ax2 + bx + c 的最值由什么决定? 二次函数 y = ax2 + bx + c 的最值由 a 的符号、对称轴的位置及自变量的取值范围决定. 思考2 当自变量 x 为全体实数时,二次函数 y = ax2 + bx + c 的最值是多少? 思考3 当自变量 x 限定范围时,二次函数 y = ax2 + bx + c 的最值如何确定? 先判断 是否在限定范围内,若在,则二次函数在 x = 时取得一个最值,另一个最值需考察限定范围的端点处来决定;若不在,则根据二次函数的增减性确定其最值. 知识点2: 二次函数与几何图形面积的最值 例2 用总长为 60 m 的篱笆围成矩形场地,矩形面积 S (m2) 随矩形一边长 l (m) 的变化而变化. 当 l 是多少米时,场地的面积 S 最大? 思考 这个问题研究的是哪两个变量之间的关系? 预设:矩形面积 S 与一边长 l 的关系. 分析:则另一边长为__(30 l ) ___m. 矩形菜园的面积 S =__(30 l )l = l2 + 30l___. 问题 当 l 是多少米时,场地的面积 S 最大? 变式 如图,用一段长为 60 m 的篱笆围成一个一边靠墙的矩形菜园. (1) 当墙长 32 m 时,这个矩形的长、宽各为多少时,菜园的面积最大?最大面积是多少? 师生活动: 1.教师引导学生分析与矩形面积相关的量. 2.教师设问,如何用含x的代数式表示与其相邻的边的长度. 3.学生自主列函数解析式,并进行整理,讨论问题解答的正确性. 4.针对问题要求进行求解,并回答问题. 思考 这个问题研究的是哪两个变量之间的关系? 预设:矩形面积与一边长的关系. ① 设未知数,用含未知数的代数式表示相关量 解:设垂直于墙的一边长为 x m,则平行于墙的边长为 (60 2x) m. ∴ S = x(60 2x) = 2x2+60x . ② 根据题意,求出自变量的取值范围 ③ 写出二次函数解析式,并化为顶点式 ∵ S = 2x2+60x = 2(x 15)2 + 450, ④ 结合自变量的取值范围可知,该二次函数在其顶点处取得最大值 ∴ 当 x = 15 m 时,S 取最大值,此时 S最大值 = 450 m2. (2) 当墙长 18 m 时,这个矩形的长、宽各为多少时,菜园的面积最大?最大面积是多少? 想一想:当墙长发生改变时,根据问题(1),什么会发什么改变,什么不变? 解:设垂直于墙的一边长为 x m, 由 (1) 知 S = 2x2+60x = 2(x2 30x) = 2(x 15)2 + 450. ∴21≤x<30. ∵ 15<21, ∴ 当 21≤ x<30 时, S 随 x 的增大而减小, 故当 x = 21 时,S 取得最大值, 此时 S最大值= 2×(21 15)2 + 450 = 378 (m2). 归纳总结 二次函数解决几何面积最值问题的方法: 1. 求出函数解析式和自变量的取值范围; 2. 当自变量的取值范围没有限制时,可直接利用公式求它的最大值或最小值; 3. 当自变量的取值范围有所限制时,可先配成顶点式,然后画出函数图象的草图,再结合图象和自变量的范围求函数最值. 链接中考 1. (河北期末) 如图,嘉嘉欲借助院子里的一面长 15 m 的墙,想用长为 40 m 的网绳围成一个矩形 ABCD 给奶奶养鸡,怎样使矩形 ABCD 的面积最大呢 同学淇淇帮她解决了这个问题,淇淇的思路是:设 BC 的边长为 x m. 矩形 ABCD 的面积为 S m2 不考虑其他因素,请帮他们回答下列问题: (1) 求 S 与 x 的函数关系式. 直接写出 x 的取值范围; (2) x 为何值时,矩形 ABCD 的面积最大 师生活动: 1.两名学生板演,其余学生在练习本上做题。 2小组内批阅。 3.对板演的内容进行评价纠错。 三、当堂练习,巩固所学 1. 广场上喷水池中的喷头微露水面,喷出的水线呈一条抛物线,水线上水珠的高度 y 米关于水珠和喷头的水平距离 x 米的函数解析式是 (0≤x≤4),那么水珠的高度达到最大时,水珠与喷头的水平距离是( ) A. 1 米 B. 2 米 C. 5 米 D. 6 米 2. 已知直角三角形的两直角边之和为 8,则该三角形的面积的最大值是______. 3. 某小区要在一块空地上修建一个矩形绿化带 ABCD,绿化带一边靠墙 (墙长 25 m),另三边用总长为 40 m 的栅栏围住.设绿化带的边长 BD 为 x m,绿化带的面积为 y m2. (1) 求 y 与 x 之间的函数关系式,并写出自变量的取值范围. (2) 当 x 为何值时,满足条件的绿化带的面积最大? 设计意图: 创设现实生活问题情境,吸引学生兴趣,培养学生用数学眼光观察现实世界的意识. 设计意图:通过追问为学生提供解决此类问题的思路,让学生在问题解决的过程中体会二次函数与实际问题的联系,用二次函数的最大值等知识刻画实际问题中的最大高度. 设计意图:通过思考问题帮助同学总结求解二次函数最值的几种情况和方法,构建知识成体系. 设计意图:借助分析和问题,指导学生解决此类问题的基本过程和方法,使不同水平的学生有不同层次的发现,加深对本题数量关系的理解,这样会使学生对函数有一个更深层次的理解和认识,同时便于他们今后应用这一数学模型解决实际问题。 设计意图:根据墙长的变化,面积的表达式也在变化,同时自变量的取值范围也在变化;在求最值时,一定需要考虑自变量的取值是否在取值范围内,不在的时候根据函数草图结合自变量的范围求取最值. 设计意图:把数学问题变式到实际生活问题,让学生把数学知识运用到日常生活中,体会用数学的过程.由矩形面积变式到复合型面积,拓展了思维,以不变应万变,通过本题的训练让学生进一步体会利用二次函数解决最大面积问题的方法、过程. 设计意图: 针对本课时的主要问题,从多个角度、分层次进 行检测,达到学有所成、了解课堂学习效果的目的.
板书设计 22.3 实际问题与二次函数 第1课时 几何图形的最大面积 二次函数解决几何面积最值问题的方法: 1. 求出函数解析式和自变量的取值范围; 2. 当自变量的取值范围没有限制时,可直接利用公式 求它的最大值或最小值; 3. 当自变量的取值范围有所限制时,可先配成顶点式, 然后画出函数图象的草图,再结合图象和自变量的 范围求函数最值.
课后小结 教师与学生一起回顾本节课所学的主要内容,梳理并完善知识思维导图。
教学反思 由于本节课的内容是二次函数的应用问题,重在通过学习总结解决问题的方法,故而本节课以“启发探究式”为主线开展教学活动,以学生动手动脑探究为主,必要时加以小组合作讨论,充分调动学生学习积极性和主动性,突出学生的主体地位,达到“不但使学生学会,而且使学生会学”的目的.
同课章节目录
