2024新人教版八年级上数学 15.1.2 线段的垂直平分 第2课时 线段的垂直平分线的有关作图 课件(共35张PPT)
文档属性
| 名称 | 2024新人教版八年级上数学 15.1.2 线段的垂直平分 第2课时 线段的垂直平分线的有关作图 课件(共35张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 10.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-25 06:03:45 | ||
图片预览





文档简介
(共35张PPT)
人教版(2024)
八年级上册
15.1.2 线段的垂直平分
第2课时 线段的垂直平分
线的有关作图
第十五章 · 轴对称
线段的垂直平分线的有关作图
知识目标
1.理解并掌握用尺规作线段的垂直平分线的方法;明确轴对称图形或成轴对称的两个图形的对称轴的定义及性质;学会过直线外一点作已知直线的垂线的步骤。
2.知道上述作图过程所依赖的几何定理。
能力目标
1.通过动手实践,熟练完成指定条件下的尺规作图任务,提升空间想象与精准绘图技能。
2.基于已学知识分析作图可行性,解释每一步设计的数学原理,培养从条件到结论的严谨思维习惯。
素质目标
1.树立“有理有据”的探究意识,尊重数学规律,反对盲目猜测;通过验证作图结果是否符合预期,形成批判性思维。
2.欣赏轴对称在生活中的应用美,激发创造性地运用对称原理进行图案设计的兴趣。
教学难点
教学重点
尺规作图的具体方法(尤其是垂直平分线、对称轴、过定点垂线的标准化步骤)
理解作图背后的几何本质
知识讲解
03
对应练习
05
情景创设
01
课堂小结
07
例题讲解
04
链接中考
06
新知探索
02
情景导入
合作探究
抽象概念
示范讲解
课堂练习
课堂小结
情景激趣
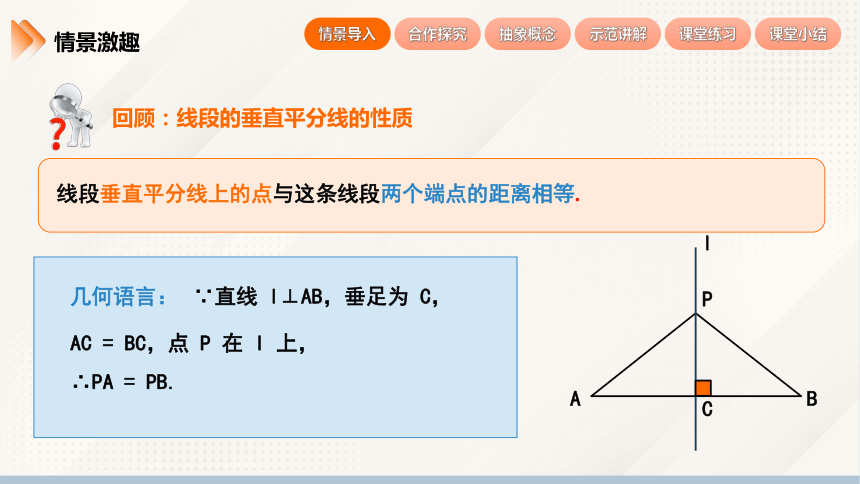
回顾:线段的垂直平分线的性质
线段垂直平分线上的点与这条线段两个端点的距离相等.
∵直线 l⊥AB,垂足为 C,
AC = BC,点 P 在 l 上,
∴PA = PB.
几何语言:
P
A
B
l
C
情景导入
合作探究
抽象概念
示范讲解
课堂练习
课堂小结
情景激趣
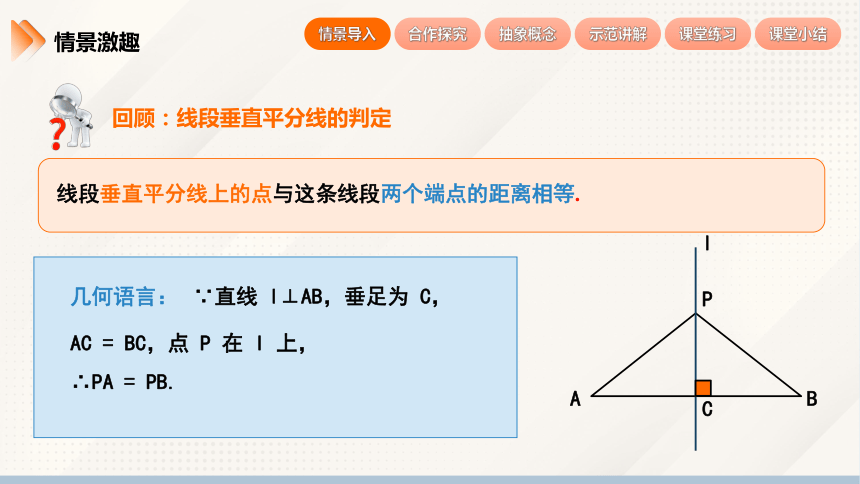
回顾:线段垂直平分线的判定
线段垂直平分线上的点与这条线段两个端点的距离相等.
∵直线 l⊥AB,垂足为 C,
AC = BC,点 P 在 l 上,
∴PA = PB.
几何语言:
P
A
B
l
C
情景导入
合作探究
抽象概念
示范讲解
课堂练习
课堂小结
情景激趣
不用一颗钉子,全靠木头咬合!古人如何做到千年不倒?
情景导入
合作探究
抽象概念
示范讲解
课堂练习
课堂小结
情景激趣
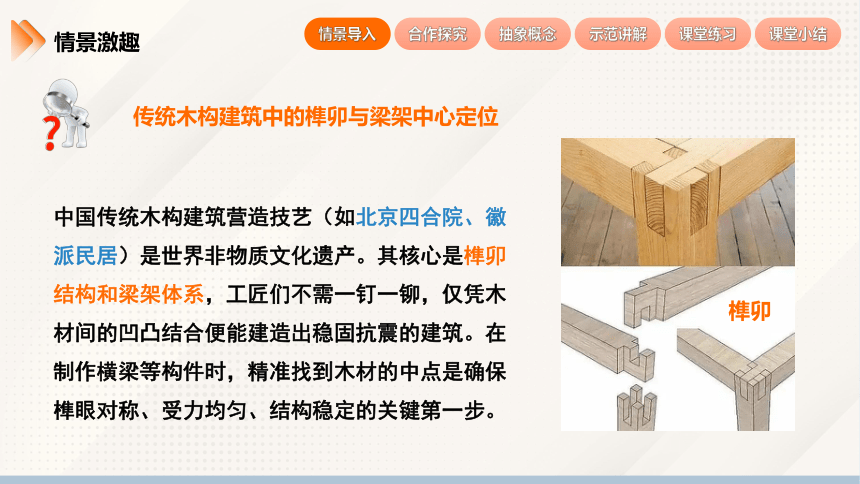
传统木构建筑中的榫卯与梁架中心定位
中国传统木构建筑营造技艺(如北京四合院、徽派民居)是世界非物质文化遗产。其核心是榫卯结构和梁架体系,工匠们不需一钉一铆,仅凭木材间的凹凸结合便能建造出稳固抗震的建筑。在制作横梁等构件时,精准找到木材的中点是确保榫眼对称、受力均匀、结构稳定的关键第一步。
榫卯
情景导入
合作探究
抽象概念
示范讲解
课堂练习
课堂小结
情景激趣
传统木构建筑中的榫卯与梁架中心定位
中国传统木构建筑营造技艺(如北京四合院、徽派民居)是世界非物质文化遗产。其核心是榫卯结构和梁架体系,工匠们不需一钉一铆,仅凭木材间的凹凸结合便能建造出稳固抗震的建筑。在制作横梁等构件时,精准找到木材的中点是确保榫眼对称、受力均匀、结构稳定的关键第一步。
情景导入
合作探究
抽象概念
示范讲解
课堂练习
课堂小结
情景激趣
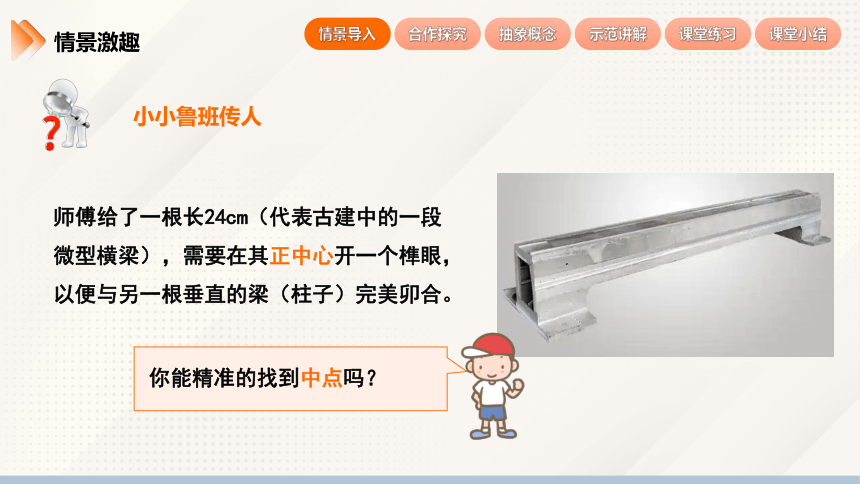
小小鲁班传人
师傅给了一根长24cm(代表古建中的一段微型横梁),需要在其正中心开一个榫眼,以便与另一根垂直的梁(柱子)完美卯合。
你能精准的找到中点吗?
情景导入
合作探究
抽象概念
示范讲解
课堂练习
课堂小结
列举实例,复习旧知
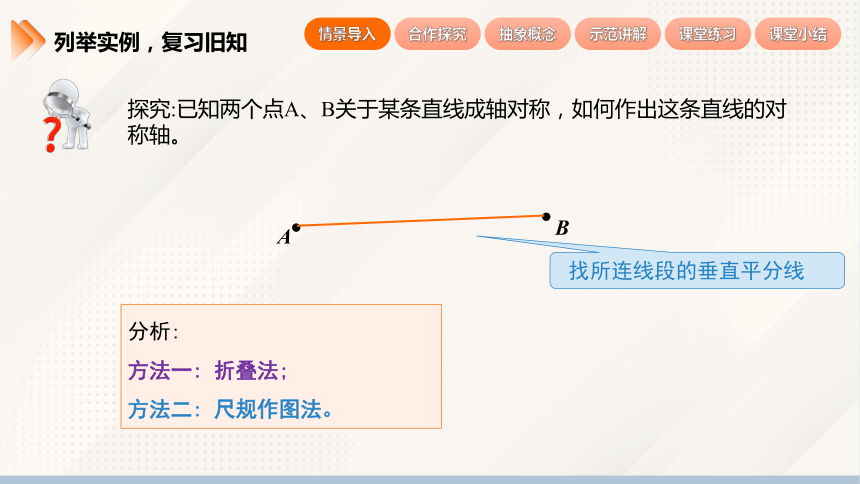
探究:已知两个点A、B关于某条直线成轴对称,如何作出这条直线的对称轴。
A
B
找所连线段的垂直平分线
分析:
方法一: 折叠法;
方法二: 尺规作图法。
情景导入
合作探究
抽象概念
示范讲解
课堂练习
课堂小结
列举实例,复习旧知
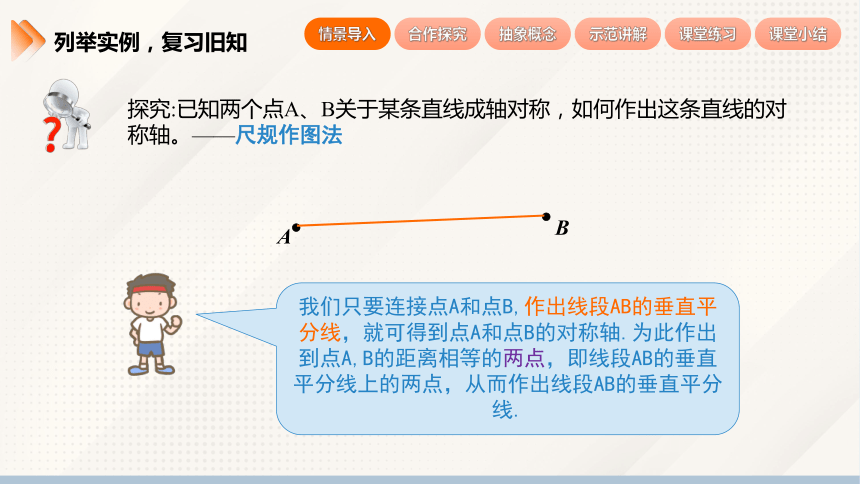
探究:已知两个点A、B关于某条直线成轴对称,如何作出这条直线的对称轴。——尺规作图法
A
B
我们只要连接点A和点B,作出线段AB的垂直平分线,就可得到点A和点B的对称轴.为此作出到点A,B的距离相等的两点,即线段AB的垂直平分线上的两点,从而作出线段AB的垂直平分线.
分析问题,寻找对应
如果点 M,N 都在线段 AB 的垂直平分线上,那么我们能画出线段 AB 的垂直平分线吗?为什么?
分组讨论
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
A
B
M
N
可以. 如图,过点 M,N 画一条直线,这条直线就是线段 AB 的垂直平分线.
理由:因为点 M,N 都在线段 AB 的垂直平分线上,而两点确定一条直线,所以直线 MN 就是线段 AB 的垂直平分线.
分析问题,寻找对应
如图,点A和点B关于某条直线成轴对称,你能作出这条直线吗?
分组尝试
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
A
B
C
D
作法:
(1)分别以点A,B为圆心,以大于AB的长为半径作弧,两弧交于C,D两点.
(2)作直线CD.
CD即为所求.
特别说明:这个作法实际上就是线段垂直平分线的尺规作图,我们也可以用这种方法确定线段的中点.
例题讲解
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
例1
如图,A,B是路边两个新建小区,要在公路边增设一个公共汽车站.使两个小区到车站的路程一样长,该公共汽车站应建在什么地方?
A
B
分析:增设的公共汽车站要满足到两个小区的路程一样长,应在线段AB的垂直平分线上,又要在公路边上,所以找到AB垂直平分线与公路的交点便是.
公共汽车站
线段的垂直平分线的有关作图
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
作对称轴
学习了线段的垂直平分线的作法,就可以作对称轴了.
任意找一对对应点,作出连接它们的线段的垂直平分线,就可以得到这两个图形的对称轴.
1.如果两个图形成轴对称,怎样作出对称轴?
A
A'
l
线段的垂直平分线的有关作图
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
作对称轴
2.对于轴对称图形,怎样作出对称轴?
任意找一对对称点,作出连接它们的线段的垂直平分线,就可以得到此图形的对称轴.
A
A'
l
你能作出这个五角星的所有对称轴吗?
线段的垂直平分线的有关作图
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
作对称轴
2.对于轴对称图形,怎样作出对称轴?
任意找一对对称点,作出连接它们的线段的垂直平分线,就可以得到此图形的对称轴.
你能作出这个五角星的所有对称轴吗?
五角星有五条对称轴.
线段的垂直平分线的有关作图
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
利用线段的垂直平分线的作法画对称轴:
1
找:无论是作成轴对称的两个图形的对称轴,还是作轴对称图形的对称轴,其关键都是找出图形中的任意一对对称点;
2
连:连接这对对称点;
3
作:作所连线段的垂直平分线,该垂直平分线就是成轴对称的两个图形或轴对称图形的对称轴.
例题讲解
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
作出下列图形的一条对称轴.
例2
A
B
A
B
例题讲解
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
作出下列图形的一条对称轴.和同学比较一下,你们作出的对称轴一样吗?
例3
例题讲解
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
例4
尺规作图:经过已知直线外一点作这条直线的垂线.
已知:直线 AB 和 AB 外一点 C .
求作:AB 的垂线,使它经过点 C.
A
B
C
分析:假设所求作直线已经作出,
则它不仅过点 C 与直线 AB 垂直,而且是连接 AB 上与垂足距离相等的两点的线段的垂直平分线.
先确定这两点
在直线 AB 上且与点 C 的距离相等即可
例题讲解
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
例4
尺规作图:经过已知直线外一点作这条直线的垂线.
已知:直线 AB 和 AB 外一点 C .
求作:AB 的垂线,使它经过点 C.
A
B
C
解:(1)以点 C 为圆心,适当长为半径作弧,交直线 AB 于点 D 和点 E.
E
D
由(1)可知,点 C 在线段 DE 的垂直平分线上.
因而再作出与 D,E 距离相等的另一点 F,就能得到线段 DE 的垂直平分线.
例题讲解
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
例4
尺规作图:经过已知直线外一点作这条直线的垂线.
已知:直线 AB 和 AB 外一点 C .
求作:AB 的垂线,使它经过点 C.
A
B
C
解:(2)分别以点 D 和点 E 为圆心,大于DE 的长为半径作弧,两弧相交于点 F.
E
D
(3)作直线 CF.
直线 CF 就是所求作的垂线.
F
例题讲解
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
例5
尺规作图:经过已知直线上的一点作这条直线的垂线 .
已知:直线 AB 和 AB 上一点 C(如图).
求作:AB 的垂线,使它经过点 C.
解:(1)以点 C 为圆心,适当长为半径作弧,交直线 AB 于点 D 和点 E;
(2)分别以点 D 和点 E 为圆心,大于DE 的长为半径作弧,两弧相交于点 F;
A
B
C
D
E
F
(3)作直线 CF.
直线 CF 就是所求作的垂线.
对照练习
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
(1)
(2)
(3)
(4)
1. 如图,与图形(1)成轴对称的是哪个图形?作出它们的对称轴.
对照练习
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
2. 如图,在△AEF 中,尺规作图如下:分别以点 E 和点 F 为圆心,大于 EF 的长为半径作弧,两弧相交于 G,H 两点,作直线 GH,交 EF 于点 O,连接 AO,则下列结论正确的是( )
A. AO 垂直平分EF B. GH 垂直平分EF
C. GH 平分AF D. 以上都不对
B
对照练习
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
3.尺规作图要求:Ⅰ、过直线外一点作这条直线的垂线;Ⅱ、作线段的垂直平分线;Ⅲ、过直线上一点作这条直线的垂线;Ⅳ、作角的平分线.
如图是按上述要求排乱顺序的尺规作图:
则正确的配对是( )
A.①﹣Ⅳ,②﹣Ⅱ,③﹣Ⅰ,④﹣Ⅲ
B.①﹣Ⅳ,②﹣Ⅲ,③﹣Ⅱ,④﹣Ⅰ
C.①﹣Ⅱ,②﹣Ⅳ,③﹣Ⅲ,④﹣Ⅰ
D.①﹣Ⅳ,②﹣Ⅰ,③﹣Ⅱ,④﹣Ⅲ
D
① ② ③ ④
对照练习
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
4.如图,角是轴对称图形吗?如果是,它的对称轴是什么?
角是轴对称图形,角平分线所在的直线就是角的对称轴.
链接中考
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
(2022·湖南衡阳·中考真题)如图,在△ABC中,分别以点A和点B为圆心,大于AB的长为半径画弧,两弧相交于点M,N,作直线MN,交BC于点D,连接AD.若△ADC的周长为10,AB=7,则△ABC的周长为( )
A.7
B.14
C.17
D.20
[答案]C
[详解]解:由作图可得:MN是AB的垂直平分线,
∴DA=DB,
∵AD=DB=4,C△ADC=AD+AC+DC=4+AC+DC=10,
∴AC+DC=6,C△ABC=AB+BC+AC=AB+BD+DC+AC=AB+AD+DC+AC=7+4+6=17,故答案为:17
课堂小结
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
我亲历了什么
我知道了什么
我会什么
明确轴对称图形或成轴对称的两个图形的对称轴的定义及性质
学会过直线外一点作已知直线的垂线的步骤
掌握用尺规作线段的垂直平分线的方法
课堂小结
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
A
B
C
D
作法:
(1)分别以点A,B为圆心,以大于AB的长为半径作弧,两弧交于C,D两点.
(2)作直线CD.
CD即为所求.
特别说明:这个作法实际上就是线段垂直平分线的尺规作图,我们也可以用这种方法确定线段的中点.
线段垂直平分线的尺规作图
课堂小结
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
利用线段的垂直平分线的作法画对称轴:
1
找:无论是作成轴对称的两个图形的对称轴,还是作轴对称图形的对称轴,其关键都是找出图形中的任意一对对称点;
2
连:连接这对对称点;
3
作:作所连线段的垂直平分线,该垂直平分线就是成轴对称的两个图形或轴对称图形的对称轴.
课堂小结
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
尺规作图:经过已知直线外一点作这条直线的垂线.
尺规作图:经过已知直线上的一点作这条直线的垂线 .
A
B
C
E
D
F
A
B
C
D
E
F
课堂小结
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
课后作业
A层:P69习题 15.1:10、12题.
B层:P69习题 15.1:11题.
下 课
人教版(2024)
八年级上册
15.1.2 线段的垂直平分
第2课时 线段的垂直平分
线的有关作图
第十五章 · 轴对称
线段的垂直平分线的有关作图
知识目标
1.理解并掌握用尺规作线段的垂直平分线的方法;明确轴对称图形或成轴对称的两个图形的对称轴的定义及性质;学会过直线外一点作已知直线的垂线的步骤。
2.知道上述作图过程所依赖的几何定理。
能力目标
1.通过动手实践,熟练完成指定条件下的尺规作图任务,提升空间想象与精准绘图技能。
2.基于已学知识分析作图可行性,解释每一步设计的数学原理,培养从条件到结论的严谨思维习惯。
素质目标
1.树立“有理有据”的探究意识,尊重数学规律,反对盲目猜测;通过验证作图结果是否符合预期,形成批判性思维。
2.欣赏轴对称在生活中的应用美,激发创造性地运用对称原理进行图案设计的兴趣。
教学难点
教学重点
尺规作图的具体方法(尤其是垂直平分线、对称轴、过定点垂线的标准化步骤)
理解作图背后的几何本质
知识讲解
03
对应练习
05
情景创设
01
课堂小结
07
例题讲解
04
链接中考
06
新知探索
02
情景导入
合作探究
抽象概念
示范讲解
课堂练习
课堂小结
情景激趣
回顾:线段的垂直平分线的性质
线段垂直平分线上的点与这条线段两个端点的距离相等.
∵直线 l⊥AB,垂足为 C,
AC = BC,点 P 在 l 上,
∴PA = PB.
几何语言:
P
A
B
l
C
情景导入
合作探究
抽象概念
示范讲解
课堂练习
课堂小结
情景激趣
回顾:线段垂直平分线的判定
线段垂直平分线上的点与这条线段两个端点的距离相等.
∵直线 l⊥AB,垂足为 C,
AC = BC,点 P 在 l 上,
∴PA = PB.
几何语言:
P
A
B
l
C
情景导入
合作探究
抽象概念
示范讲解
课堂练习
课堂小结
情景激趣
不用一颗钉子,全靠木头咬合!古人如何做到千年不倒?
情景导入
合作探究
抽象概念
示范讲解
课堂练习
课堂小结
情景激趣
传统木构建筑中的榫卯与梁架中心定位
中国传统木构建筑营造技艺(如北京四合院、徽派民居)是世界非物质文化遗产。其核心是榫卯结构和梁架体系,工匠们不需一钉一铆,仅凭木材间的凹凸结合便能建造出稳固抗震的建筑。在制作横梁等构件时,精准找到木材的中点是确保榫眼对称、受力均匀、结构稳定的关键第一步。
榫卯
情景导入
合作探究
抽象概念
示范讲解
课堂练习
课堂小结
情景激趣
传统木构建筑中的榫卯与梁架中心定位
中国传统木构建筑营造技艺(如北京四合院、徽派民居)是世界非物质文化遗产。其核心是榫卯结构和梁架体系,工匠们不需一钉一铆,仅凭木材间的凹凸结合便能建造出稳固抗震的建筑。在制作横梁等构件时,精准找到木材的中点是确保榫眼对称、受力均匀、结构稳定的关键第一步。
情景导入
合作探究
抽象概念
示范讲解
课堂练习
课堂小结
情景激趣
小小鲁班传人
师傅给了一根长24cm(代表古建中的一段微型横梁),需要在其正中心开一个榫眼,以便与另一根垂直的梁(柱子)完美卯合。
你能精准的找到中点吗?
情景导入
合作探究
抽象概念
示范讲解
课堂练习
课堂小结
列举实例,复习旧知
探究:已知两个点A、B关于某条直线成轴对称,如何作出这条直线的对称轴。
A
B
找所连线段的垂直平分线
分析:
方法一: 折叠法;
方法二: 尺规作图法。
情景导入
合作探究
抽象概念
示范讲解
课堂练习
课堂小结
列举实例,复习旧知
探究:已知两个点A、B关于某条直线成轴对称,如何作出这条直线的对称轴。——尺规作图法
A
B
我们只要连接点A和点B,作出线段AB的垂直平分线,就可得到点A和点B的对称轴.为此作出到点A,B的距离相等的两点,即线段AB的垂直平分线上的两点,从而作出线段AB的垂直平分线.
分析问题,寻找对应
如果点 M,N 都在线段 AB 的垂直平分线上,那么我们能画出线段 AB 的垂直平分线吗?为什么?
分组讨论
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
A
B
M
N
可以. 如图,过点 M,N 画一条直线,这条直线就是线段 AB 的垂直平分线.
理由:因为点 M,N 都在线段 AB 的垂直平分线上,而两点确定一条直线,所以直线 MN 就是线段 AB 的垂直平分线.
分析问题,寻找对应
如图,点A和点B关于某条直线成轴对称,你能作出这条直线吗?
分组尝试
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
A
B
C
D
作法:
(1)分别以点A,B为圆心,以大于AB的长为半径作弧,两弧交于C,D两点.
(2)作直线CD.
CD即为所求.
特别说明:这个作法实际上就是线段垂直平分线的尺规作图,我们也可以用这种方法确定线段的中点.
例题讲解
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
例1
如图,A,B是路边两个新建小区,要在公路边增设一个公共汽车站.使两个小区到车站的路程一样长,该公共汽车站应建在什么地方?
A
B
分析:增设的公共汽车站要满足到两个小区的路程一样长,应在线段AB的垂直平分线上,又要在公路边上,所以找到AB垂直平分线与公路的交点便是.
公共汽车站
线段的垂直平分线的有关作图
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
作对称轴
学习了线段的垂直平分线的作法,就可以作对称轴了.
任意找一对对应点,作出连接它们的线段的垂直平分线,就可以得到这两个图形的对称轴.
1.如果两个图形成轴对称,怎样作出对称轴?
A
A'
l
线段的垂直平分线的有关作图
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
作对称轴
2.对于轴对称图形,怎样作出对称轴?
任意找一对对称点,作出连接它们的线段的垂直平分线,就可以得到此图形的对称轴.
A
A'
l
你能作出这个五角星的所有对称轴吗?
线段的垂直平分线的有关作图
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
作对称轴
2.对于轴对称图形,怎样作出对称轴?
任意找一对对称点,作出连接它们的线段的垂直平分线,就可以得到此图形的对称轴.
你能作出这个五角星的所有对称轴吗?
五角星有五条对称轴.
线段的垂直平分线的有关作图
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
利用线段的垂直平分线的作法画对称轴:
1
找:无论是作成轴对称的两个图形的对称轴,还是作轴对称图形的对称轴,其关键都是找出图形中的任意一对对称点;
2
连:连接这对对称点;
3
作:作所连线段的垂直平分线,该垂直平分线就是成轴对称的两个图形或轴对称图形的对称轴.
例题讲解
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
作出下列图形的一条对称轴.
例2
A
B
A
B
例题讲解
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
作出下列图形的一条对称轴.和同学比较一下,你们作出的对称轴一样吗?
例3
例题讲解
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
例4
尺规作图:经过已知直线外一点作这条直线的垂线.
已知:直线 AB 和 AB 外一点 C .
求作:AB 的垂线,使它经过点 C.
A
B
C
分析:假设所求作直线已经作出,
则它不仅过点 C 与直线 AB 垂直,而且是连接 AB 上与垂足距离相等的两点的线段的垂直平分线.
先确定这两点
在直线 AB 上且与点 C 的距离相等即可
例题讲解
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
例4
尺规作图:经过已知直线外一点作这条直线的垂线.
已知:直线 AB 和 AB 外一点 C .
求作:AB 的垂线,使它经过点 C.
A
B
C
解:(1)以点 C 为圆心,适当长为半径作弧,交直线 AB 于点 D 和点 E.
E
D
由(1)可知,点 C 在线段 DE 的垂直平分线上.
因而再作出与 D,E 距离相等的另一点 F,就能得到线段 DE 的垂直平分线.
例题讲解
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
例4
尺规作图:经过已知直线外一点作这条直线的垂线.
已知:直线 AB 和 AB 外一点 C .
求作:AB 的垂线,使它经过点 C.
A
B
C
解:(2)分别以点 D 和点 E 为圆心,大于DE 的长为半径作弧,两弧相交于点 F.
E
D
(3)作直线 CF.
直线 CF 就是所求作的垂线.
F
例题讲解
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
例5
尺规作图:经过已知直线上的一点作这条直线的垂线 .
已知:直线 AB 和 AB 上一点 C(如图).
求作:AB 的垂线,使它经过点 C.
解:(1)以点 C 为圆心,适当长为半径作弧,交直线 AB 于点 D 和点 E;
(2)分别以点 D 和点 E 为圆心,大于DE 的长为半径作弧,两弧相交于点 F;
A
B
C
D
E
F
(3)作直线 CF.
直线 CF 就是所求作的垂线.
对照练习
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
(1)
(2)
(3)
(4)
1. 如图,与图形(1)成轴对称的是哪个图形?作出它们的对称轴.
对照练习
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
2. 如图,在△AEF 中,尺规作图如下:分别以点 E 和点 F 为圆心,大于 EF 的长为半径作弧,两弧相交于 G,H 两点,作直线 GH,交 EF 于点 O,连接 AO,则下列结论正确的是( )
A. AO 垂直平分EF B. GH 垂直平分EF
C. GH 平分AF D. 以上都不对
B
对照练习
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
3.尺规作图要求:Ⅰ、过直线外一点作这条直线的垂线;Ⅱ、作线段的垂直平分线;Ⅲ、过直线上一点作这条直线的垂线;Ⅳ、作角的平分线.
如图是按上述要求排乱顺序的尺规作图:
则正确的配对是( )
A.①﹣Ⅳ,②﹣Ⅱ,③﹣Ⅰ,④﹣Ⅲ
B.①﹣Ⅳ,②﹣Ⅲ,③﹣Ⅱ,④﹣Ⅰ
C.①﹣Ⅱ,②﹣Ⅳ,③﹣Ⅲ,④﹣Ⅰ
D.①﹣Ⅳ,②﹣Ⅰ,③﹣Ⅱ,④﹣Ⅲ
D
① ② ③ ④
对照练习
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
4.如图,角是轴对称图形吗?如果是,它的对称轴是什么?
角是轴对称图形,角平分线所在的直线就是角的对称轴.
链接中考
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
(2022·湖南衡阳·中考真题)如图,在△ABC中,分别以点A和点B为圆心,大于AB的长为半径画弧,两弧相交于点M,N,作直线MN,交BC于点D,连接AD.若△ADC的周长为10,AB=7,则△ABC的周长为( )
A.7
B.14
C.17
D.20
[答案]C
[详解]解:由作图可得:MN是AB的垂直平分线,
∴DA=DB,
∵AD=DB=4,C△ADC=AD+AC+DC=4+AC+DC=10,
∴AC+DC=6,C△ABC=AB+BC+AC=AB+BD+DC+AC=AB+AD+DC+AC=7+4+6=17,故答案为:17
课堂小结
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
我亲历了什么
我知道了什么
我会什么
明确轴对称图形或成轴对称的两个图形的对称轴的定义及性质
学会过直线外一点作已知直线的垂线的步骤
掌握用尺规作线段的垂直平分线的方法
课堂小结
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
A
B
C
D
作法:
(1)分别以点A,B为圆心,以大于AB的长为半径作弧,两弧交于C,D两点.
(2)作直线CD.
CD即为所求.
特别说明:这个作法实际上就是线段垂直平分线的尺规作图,我们也可以用这种方法确定线段的中点.
线段垂直平分线的尺规作图
课堂小结
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
利用线段的垂直平分线的作法画对称轴:
1
找:无论是作成轴对称的两个图形的对称轴,还是作轴对称图形的对称轴,其关键都是找出图形中的任意一对对称点;
2
连:连接这对对称点;
3
作:作所连线段的垂直平分线,该垂直平分线就是成轴对称的两个图形或轴对称图形的对称轴.
课堂小结
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
尺规作图:经过已知直线外一点作这条直线的垂线.
尺规作图:经过已知直线上的一点作这条直线的垂线 .
A
B
C
E
D
F
A
B
C
D
E
F
课堂小结
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
课后作业
A层:P69习题 15.1:10、12题.
B层:P69习题 15.1:11题.
下 课
同课章节目录
