2.3 课时2 作已知直线的平行线或垂线 课件(共15张PPT) 2025-2026学年青岛版数学八年级上册
文档属性
| 名称 | 2.3 课时2 作已知直线的平行线或垂线 课件(共15张PPT) 2025-2026学年青岛版数学八年级上册 |  | |
| 格式 | pptx | ||
| 文件大小 | 8.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-23 21:18:43 | ||
图片预览






文档简介
(共15张PPT)
第2章 全等三角形
2.3 课时2 作已知直线的平行线或垂线
1.理解和掌握尺规作图:过直线外一点作已知直线的平行线或垂线;
2.探索尺规作图的作法,积累数学活动经验.
用圆规和直尺能不能作出正七边形、正九边形、正十一边形、正十三边形、正十七边形呢
这个问题困扰了2000多年,
一直未解.
数学家欧几里得
数学家高斯
出乎人意料之外的是,这个难题竞被年仅19岁的高斯解决了. 他用直尺和圆规作出了正十七边形.
想一想:同一平面内两条直线有什么样的位置关系?
平行或相交
垂直是相交的一种特殊形式
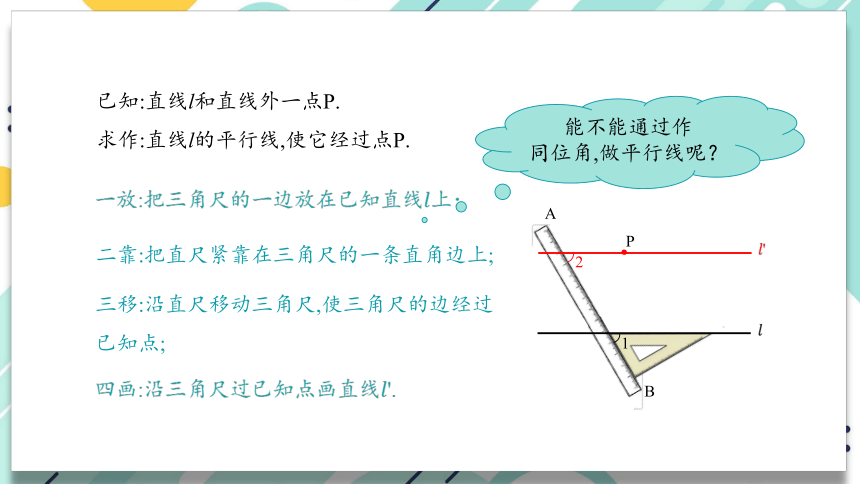
已知:直线l和直线外一点P.
求作:直线l的平行线,使它经过点P.
P
A
B
1
'
2
一放:把三角尺的一边放在已知直线上;
二靠:把直尺紧靠在三角尺的一条直角边上;
三移:沿直尺移动三角尺,使三角尺的边经过已知点;
四画:沿三角尺过已知点画直线'.
能不能通过作
同位角,做平行线呢?
作法:如图
1.过点P作直线MN,交直线l于点N;
2.作∠MPQ=∠PNK,其中K为l上不与N重合的任意一点,点Q与K位于MN同侧;
3.作直线PQ.
已知:直线 l 和 l 外一点P.
求作:直线 l 的垂线,使它经过点P.
作法:如图
1.以点P为圆心,在直线l的另一侧取一点K,以PK为半径作弧,交直线l于点M,N;
2.分别以点M,N为圆心,大于MN的长为半径作弧,两弧交于点Q;
3.作直线PQ.
M
N
K
Q
例2 已知直角三角形的斜边和一条直角边,求作这个直角三角形.
已知:线段m,n(m>n).
求作:Rt△ABC,使∠C=90°,AB=m,AC=n.
作法:如图.
1.作直线CE⊥CD;
2.在CE上截取CA=n;
3.以点A为圆心,以m为半径作弧,交CD于点B;
4.连接AB.
△ABC就是所求作的直角三角形.
1.根据下列已知条件,不能画出唯一的△ABC的是( )
A.AB=5,BC=3,∠A=30°
B.AB=5,BC=3,AC=6
C.AB=10,BC=20,∠B=80°
D.∠A=50°,∠B=60°,AB=4
A
2.如图所示,直线MN,PQ交于点O.R为MN,PQ外一点,过点R画
直线AB//PQ,直线CD∥MN.
Q
N
M
P
O
A
B
R
C
D
解:如图所示
3.如图,分别过点P作直线AB的垂线.
P
P
A
B
A
B
P
A
B
尺规作图
过直线外一点作已知直线的平行线.
过直线外一点作已知直线的垂线.
第2章 全等三角形
2.3 课时2 作已知直线的平行线或垂线
1.理解和掌握尺规作图:过直线外一点作已知直线的平行线或垂线;
2.探索尺规作图的作法,积累数学活动经验.
用圆规和直尺能不能作出正七边形、正九边形、正十一边形、正十三边形、正十七边形呢
这个问题困扰了2000多年,
一直未解.
数学家欧几里得
数学家高斯
出乎人意料之外的是,这个难题竞被年仅19岁的高斯解决了. 他用直尺和圆规作出了正十七边形.
想一想:同一平面内两条直线有什么样的位置关系?
平行或相交
垂直是相交的一种特殊形式
已知:直线l和直线外一点P.
求作:直线l的平行线,使它经过点P.
P
A
B
1
'
2
一放:把三角尺的一边放在已知直线上;
二靠:把直尺紧靠在三角尺的一条直角边上;
三移:沿直尺移动三角尺,使三角尺的边经过已知点;
四画:沿三角尺过已知点画直线'.
能不能通过作
同位角,做平行线呢?
作法:如图
1.过点P作直线MN,交直线l于点N;
2.作∠MPQ=∠PNK,其中K为l上不与N重合的任意一点,点Q与K位于MN同侧;
3.作直线PQ.
已知:直线 l 和 l 外一点P.
求作:直线 l 的垂线,使它经过点P.
作法:如图
1.以点P为圆心,在直线l的另一侧取一点K,以PK为半径作弧,交直线l于点M,N;
2.分别以点M,N为圆心,大于MN的长为半径作弧,两弧交于点Q;
3.作直线PQ.
M
N
K
Q
例2 已知直角三角形的斜边和一条直角边,求作这个直角三角形.
已知:线段m,n(m>n).
求作:Rt△ABC,使∠C=90°,AB=m,AC=n.
作法:如图.
1.作直线CE⊥CD;
2.在CE上截取CA=n;
3.以点A为圆心,以m为半径作弧,交CD于点B;
4.连接AB.
△ABC就是所求作的直角三角形.
1.根据下列已知条件,不能画出唯一的△ABC的是( )
A.AB=5,BC=3,∠A=30°
B.AB=5,BC=3,AC=6
C.AB=10,BC=20,∠B=80°
D.∠A=50°,∠B=60°,AB=4
A
2.如图所示,直线MN,PQ交于点O.R为MN,PQ外一点,过点R画
直线AB//PQ,直线CD∥MN.
Q
N
M
P
O
A
B
R
C
D
解:如图所示
3.如图,分别过点P作直线AB的垂线.
P
P
A
B
A
B
P
A
B
尺规作图
过直线外一点作已知直线的平行线.
过直线外一点作已知直线的垂线.
同课章节目录
