1.1 课时1 具有相反意义的量 课件(共17张PPT) 2025-2026学年数学冀教版(2024)七年级上册
文档属性
| 名称 | 1.1 课时1 具有相反意义的量 课件(共17张PPT) 2025-2026学年数学冀教版(2024)七年级上册 |  | |
| 格式 | pptx | ||
| 文件大小 | 30.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-25 06:08:04 | ||
图片预览






文档简介
1.1 课时1 具有相反意义的量
第一章 有理数
1.理解具有相反意义的量的含义,体会相反意义的量在现实中的应用;
2.能分析并写出具有相反意义的量;
3.能正确运用“+”、“?”表示相反意义的量
?
学习目标
1.小学数学中我们学过哪些数?
2.举例说明这些数的特征.
整数,自然数,分数,小数,奇数,偶数…
整数:1、3、34、679…
自然数:0、2、3、6…
小数:1.526、0.259…
奇数:1、3、7、11、343…
偶数:2、4、6、1110…
分数: 、 、 、 …
想一想 这些数足够表示我们生活中常见的量吗?
回顾
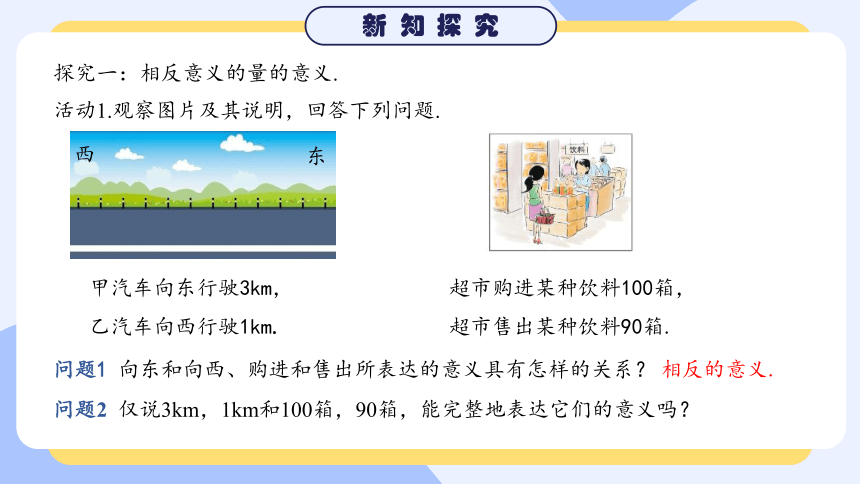
活动1.观察图片及其说明,回答下列问题.
问题1 向东和向西、购进和售出所表达的意义具有怎样的关系?
甲汽车向东行驶3km,
乙汽车向西行驶1km.
超市购进某种饮料100箱,
超市售出某种饮料90箱.
东
西
相反的意义.
探究一:相反意义的量的意义.
问题2 仅说3km,1km和100箱,90箱,能完整地表达它们的意义吗?
活动2.判断下列语句中是否有相反意义的量,如果有请找出,没有,说明理由.
(1)知识竞赛中,得20分和扣10分;
(3)一辆公共汽车在一个停车站下去10名乘客和上来8名乘客;
√ 加20分,扣10分
√ 下去10名,上来8名
(2)一座水库蓄水量增加10 000m3和减少12 000m3.
√ 增加10 000m3,减少12 000m3
(4)长方形的周长是24cm和面积是27cm2.
周长24cm
面积27cm2
9cm
3cm
×
思考:具有相反意义的量有哪些条件?
具有相反意义的量的条件:
①表示同一类量;
②表示的意义相反;
③成对出现;
④带单位.
我们生活中还遇到过哪些具有相反意义的量?
活动1.阅读教材P3中的“大家谈谈”,并独立思考回答其中的问题(1)、(2).
探究二:相反意义的量的表示.
一般地,对于具有相反意义的量,我们可以把其中一种意义的量规定为正的,并在表示这个量的数的前面加上“+”(读作“正”)来表示;把与它意义相反的量规定为负的,并在表示这个量的数的前面加上“-”(读作“负”)来表示.
甲汽车向东行驶3km,
乙汽车向西行驶1km.
+3km
-1km
活动2.用“+”、“?”表示具有相反意义的量,并思考哪些常见的语义是“+”,
哪些语义是“?”.
?
1.请用表示相反意义的量的方法,完成下表:
{5940675A-B579-460E-94D1-54222C63F5DA}意义
向北走
1.8 km
向南走
3 km
盈利
30%
水位上升
30 cm
表示
方法
+1.8 km
+30 cm
-50 cm
-3km
+30%
水位下降50cm
亏损
20%
活动2.用“+”、“-”表示具有相反意义的量,并思考哪些常见的语义是“+”,
哪些语义是“-”.
2.用带“﹢”和“-”的数表示下列具有相反意义的量:
(1) 如果将开进汽车站汽车28辆记作+28辆,那么从该汽车站开出汽车24辆,可记作_____辆.
(2) 如果把公司第一季度亏损2万元记作-2万元,那么第二季度盈利2.5万元,可记作_______万元.
(3)如果规定收入为正,那么:小亮家今年收入34200元,可记作_________元;支出27450元,可记作__________元.
-24
+ 2.5
﹢34200
- 27450
一般情况下,把向北(东)、上升、增加、收入等规定为正,把它们的相反意义规定为负.
思考:公司第一季度盈利-2万元是什么意思?
1.《九章算术》中注有“今两算得失相反,要令正负以名之”,意思是:今有两数若其意义相反,则分别叫做正数与负数.若气温为零上10 ℃记作+10 ℃,则-3 ℃表示气温为( )
A.零上3 ℃ B.零下3℃
C.零上7 ℃ D.零下7 ℃
B
2.下列各对关系中,不具有相反意义的量的是( )
A.运进货物3吨与运出货物2吨
B.升温3℃与降温3℃
C.增加货物100吨与减少货物2 000吨
D.胜3局与亏本400元
D
3.如果盈利50元记作+50元,那么亏损30元记作 ( )
A.+30元 B. -20元 C. -30元 D.+20元
C
低于标准水位0.9米
3.(1)如果零上5℃记作+5℃,那么零下3℃记作 .
(2)东、西为两个相反方向,如果-4米表示一个物体向西运动4米,那么+2米表示 .
(3)某仓库运进面粉7.5吨记作+7.5吨,那么运出3.8吨应记作 .
(4)抗洪期间,如果水位超过标准水位1.5米记作+1.5米,那么后来记录的-0.9米表示 .
-3℃
向东运动2米
-3.8吨
5.据史料记载,孔子出生于公元前551年,如果用-551年表示孔子出生的年代,那么司马迁出生于公元前145年可表示为 年,欧阳修出生于公元1007年可表示为 年,韩非子出生于-206 年表示韩非子出生于__________ 年.
孔子
欧阳修
韩非子
-145
+1007
公元前206
司马迁
具有相反意义的量
①必须是同类量,而且是成对出现的;
②只要求意义相反,不要求数量一定相等.
第一章 有理数
1.理解具有相反意义的量的含义,体会相反意义的量在现实中的应用;
2.能分析并写出具有相反意义的量;
3.能正确运用“+”、“?”表示相反意义的量
?
学习目标
1.小学数学中我们学过哪些数?
2.举例说明这些数的特征.
整数,自然数,分数,小数,奇数,偶数…
整数:1、3、34、679…
自然数:0、2、3、6…
小数:1.526、0.259…
奇数:1、3、7、11、343…
偶数:2、4、6、1110…
分数: 、 、 、 …
想一想 这些数足够表示我们生活中常见的量吗?
回顾
活动1.观察图片及其说明,回答下列问题.
问题1 向东和向西、购进和售出所表达的意义具有怎样的关系?
甲汽车向东行驶3km,
乙汽车向西行驶1km.
超市购进某种饮料100箱,
超市售出某种饮料90箱.
东
西
相反的意义.
探究一:相反意义的量的意义.
问题2 仅说3km,1km和100箱,90箱,能完整地表达它们的意义吗?
活动2.判断下列语句中是否有相反意义的量,如果有请找出,没有,说明理由.
(1)知识竞赛中,得20分和扣10分;
(3)一辆公共汽车在一个停车站下去10名乘客和上来8名乘客;
√ 加20分,扣10分
√ 下去10名,上来8名
(2)一座水库蓄水量增加10 000m3和减少12 000m3.
√ 增加10 000m3,减少12 000m3
(4)长方形的周长是24cm和面积是27cm2.
周长24cm
面积27cm2
9cm
3cm
×
思考:具有相反意义的量有哪些条件?
具有相反意义的量的条件:
①表示同一类量;
②表示的意义相反;
③成对出现;
④带单位.
我们生活中还遇到过哪些具有相反意义的量?
活动1.阅读教材P3中的“大家谈谈”,并独立思考回答其中的问题(1)、(2).
探究二:相反意义的量的表示.
一般地,对于具有相反意义的量,我们可以把其中一种意义的量规定为正的,并在表示这个量的数的前面加上“+”(读作“正”)来表示;把与它意义相反的量规定为负的,并在表示这个量的数的前面加上“-”(读作“负”)来表示.
甲汽车向东行驶3km,
乙汽车向西行驶1km.
+3km
-1km
活动2.用“+”、“?”表示具有相反意义的量,并思考哪些常见的语义是“+”,
哪些语义是“?”.
?
1.请用表示相反意义的量的方法,完成下表:
{5940675A-B579-460E-94D1-54222C63F5DA}意义
向北走
1.8 km
向南走
3 km
盈利
30%
水位上升
30 cm
表示
方法
+1.8 km
+30 cm
-50 cm
-3km
+30%
水位下降50cm
亏损
20%
活动2.用“+”、“-”表示具有相反意义的量,并思考哪些常见的语义是“+”,
哪些语义是“-”.
2.用带“﹢”和“-”的数表示下列具有相反意义的量:
(1) 如果将开进汽车站汽车28辆记作+28辆,那么从该汽车站开出汽车24辆,可记作_____辆.
(2) 如果把公司第一季度亏损2万元记作-2万元,那么第二季度盈利2.5万元,可记作_______万元.
(3)如果规定收入为正,那么:小亮家今年收入34200元,可记作_________元;支出27450元,可记作__________元.
-24
+ 2.5
﹢34200
- 27450
一般情况下,把向北(东)、上升、增加、收入等规定为正,把它们的相反意义规定为负.
思考:公司第一季度盈利-2万元是什么意思?
1.《九章算术》中注有“今两算得失相反,要令正负以名之”,意思是:今有两数若其意义相反,则分别叫做正数与负数.若气温为零上10 ℃记作+10 ℃,则-3 ℃表示气温为( )
A.零上3 ℃ B.零下3℃
C.零上7 ℃ D.零下7 ℃
B
2.下列各对关系中,不具有相反意义的量的是( )
A.运进货物3吨与运出货物2吨
B.升温3℃与降温3℃
C.增加货物100吨与减少货物2 000吨
D.胜3局与亏本400元
D
3.如果盈利50元记作+50元,那么亏损30元记作 ( )
A.+30元 B. -20元 C. -30元 D.+20元
C
低于标准水位0.9米
3.(1)如果零上5℃记作+5℃,那么零下3℃记作 .
(2)东、西为两个相反方向,如果-4米表示一个物体向西运动4米,那么+2米表示 .
(3)某仓库运进面粉7.5吨记作+7.5吨,那么运出3.8吨应记作 .
(4)抗洪期间,如果水位超过标准水位1.5米记作+1.5米,那么后来记录的-0.9米表示 .
-3℃
向东运动2米
-3.8吨
5.据史料记载,孔子出生于公元前551年,如果用-551年表示孔子出生的年代,那么司马迁出生于公元前145年可表示为 年,欧阳修出生于公元1007年可表示为 年,韩非子出生于-206 年表示韩非子出生于__________ 年.
孔子
欧阳修
韩非子
-145
+1007
公元前206
司马迁
具有相反意义的量
①必须是同类量,而且是成对出现的;
②只要求意义相反,不要求数量一定相等.
同课章节目录
- 第一章 有理数
- 1.1 正数和负数
- 1.2 数轴
- 1.3 绝对值与相反数
- 1.4 有理数的大小
- 1.5 有理数的加法
- 1.6 有理数的减法
- 1.7 有理数的加减混合运算
- 1.8 有理数的乘法
- 1.9 有理数的除法
- 1.10 有理数的乘方
- 1.11 有理数的混合运算
- 1.12 计算器的使用
- 第二章 几何图形的初步认识
- 2.1 从生活中认识几何图形
- 2.2 点和线
- 2.3 线段长短的比较
- 2.4 线段的和与差
- 2.5 角以及角的度量
- 2.6 角的大小
- 2.7 角的和与差
- 2.8 平面图形的旋转
- 第三章 代数式
- 3.1 用字母表示数
- 3.2 代数式
- 3.3 代数式的值
- 第四章 整式的加减
- 4.1 整式
- 4.2 合并同类项
- 4.3 去括号
- 4.4 整式的加减
- 第五章 一元一次方程
- 5.1一元一次方程
- 5.2 等式的基本性质
- 5.3 解一元一次方程
- 5.4 一元一次方程的应用
