1.3 绝对值与相反数 课件(共20张PPT) 2025-2026学年数学冀教版(2024)七年级上册
文档属性
| 名称 | 1.3 绝对值与相反数 课件(共20张PPT) 2025-2026学年数学冀教版(2024)七年级上册 |  | |
| 格式 | pptx | ||
| 文件大小 | 981.2KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-25 06:07:41 | ||
图片预览





文档简介
1.3 绝对值与相反数
第一章 有理数
1.掌握绝对值的概念及其性质,能求一个有理数的绝对值;
2.理解相反数的含义和性质,会求一个数的相反数.
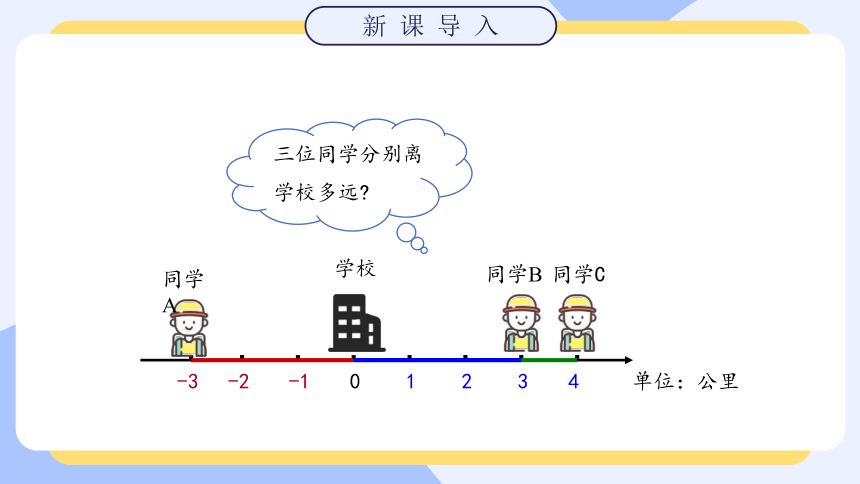
三位同学分别离学校多远?
0
1
2
3
4
-1
-2
-3
同学A
同学B
同学C
学校
单位:公里
表示4的点到原点的距离是4,
表示-2的点到原点的距离是2,
表示0的点到原点的距离是0.
活动1.画一条数轴,在数轴上标出表示4,-2,0的点,写出这些点到原点的距离.
探究一:绝对值的概念和意义.
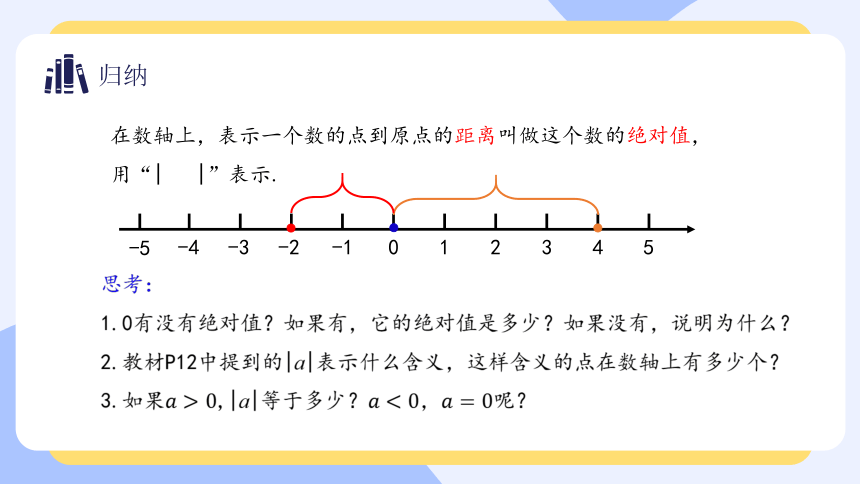
在数轴上,表示一个数的点到原点的距离叫做这个数的绝对值,用“| |”表示.
思考:
1.0有没有绝对值?如果有,它的绝对值是多少?如果没有,说明为什么?
2.教材P12中提到的|a|表示什么含义,这样含义的点在数轴上有多少个?
3.如果????>0,|a|等于多少?????<0,????=0呢?
?
0
1
2
3
4
5
-1
-2
-3
-4
-5
结论1:
0的绝对值是0;
一个正数的绝对值是正数;
一个负数的绝对值是正数;
绝对值的性质
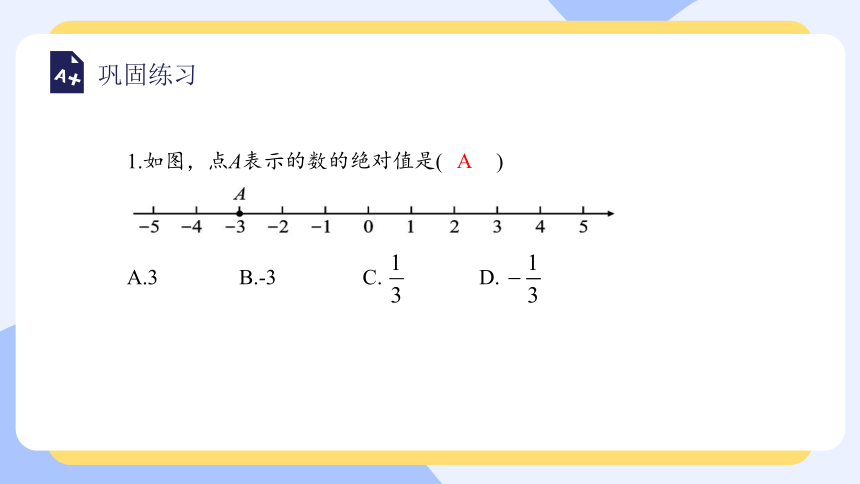
1.如图,点A表示的数的绝对值是( )
A.3 B.-3 C. D.
A
2.求下列各数的绝对值:
?53,7.5,?2.8,?34,+2
?
解:?53=53;7.5=7.5;?2.8=2.8;
?34=34;+2=2.
?
3
-3
1.5
-1.5
?16
?
16
?
①???3=3,?3=3
?
②???5=5,?5=5
?
③???16=16,?16=16
?
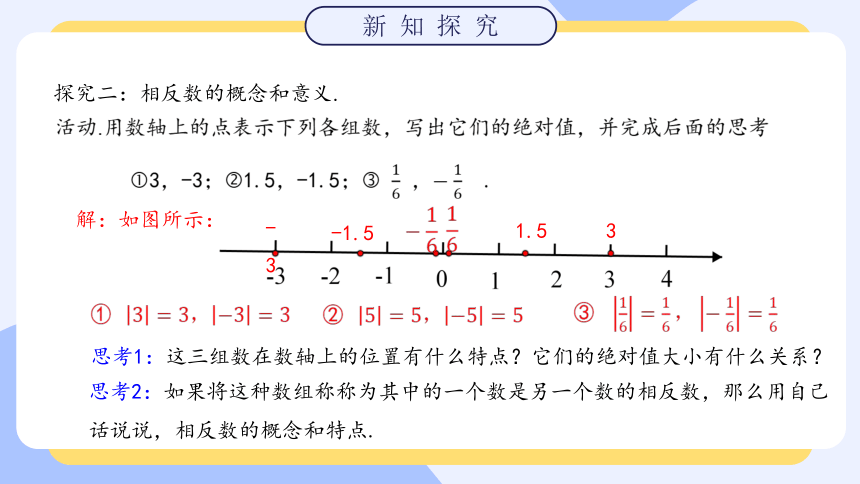
解:如图所示:
活动.用数轴上的点表示下列各组数,写出它们的绝对值,并完成后面的思考
?3,-3;?1.5,-1.5;? 16 ,?16 .
?
探究二:相反数的概念和意义.
思考1:这三组数在数轴上的位置有什么特点?它们的绝对值大小有什么关系?
思考2:如果将这种数组称称为其中的一个数是另一个数的相反数,那么用自己话说说,相反数的概念和特点.
像3和-3,5和-5这样,符号不同,绝对值相等的两个数,我们称其中一个数是另一个数的相反数,这两个数互为相反数.
思考3:0有相反数吗?如果有它的相反数是多少?如果没有,为什么?
0的相反数是0
注意:
1.互为相反数的两个数分别位于原点的两侧(0除外);互为相反数的两个数到原点的距离相等.
2.一般地,设a是一个正数,数轴上与原点的距离是a的点有两个,它们分别在原点的两侧,表示a和-a,这两点 关于原点对称.
3.表示一个数的相反数时,可以在这个数的前面添加一个“ - ”,因此,数 a 的相反数可以表示为 - a,这里 a 表示任意一个数,即它可以是正数、负数或者0.
结论1:0的绝对值是0;
一个正数的绝对值是正数;
一个负数的绝对值是正数.
绝对值的性质
结论2:0的绝对值是0;
一个正数的绝对值是正数;
一个负数的绝对值是它的相反数.
任何一个有理数的绝对值都是非负数.
1.完成下列问题,并说出你的发现:
①-(-3.5)表示______________; ∴-(-3.5)=______;
-(-a)表示______________; ∴-(-a)=______;
②-[-(-3.5)]表示_____________________; ∴-[-(-3.5)]=______;
-3.5的相反数
3.5
a的相反数
a
-3.5的相反数的相反数
-3.5
-a的相反数的相反数
-a
-[-(-a)]表示____________________; ∴-[-(-a)]=____.
结论:有理数a前面的“-”的个数为偶数时,结果为a;
有理数a前面的“-”的个数为奇数时,结果为-a.
有理数a前面的“-”的个数为偶数时,结果为a;
有理数a前面的“-”的个数为奇数时,结果为-a.
2.化简下列各数:
(1) -(- 3); (2) -(+ 2); (3) +(- 8);
(4) -[+(+ 2)]; (5) -{-[ -(+ ????)]} .
?
解:(1) -(-3)=3.
?
(2)-(+2)=-2.
?
(3)+(-8)=-8.
?
(4)-[+(+ 2)]=-(-2)=2.
?
(5)- {-[-(+????)]}=-[-(-????)]=-????.
?
绝对值与相反数
绝对值
相反数
几何意义
代数意义
在数轴上,表示数a到原点的距离.
|a|=a,(a>0)
|a|=-a,(a<0)
|a|=0,(a=0)
|a|≥0
几何意义
代数意义
符号不同,绝对值相等的两个数,互为相反数.
两个互为相反数的数在数轴上所表示的点在原点的两旁,且与原点的距离相等.
1.下列说法错误的是( )
A.-2的相反数是2 B.任何数的相反数都是负数
C.0的相反数是0 D.互为相反数的两个数相加等于0
2.?12的绝对值为( )
A.?2 B.?12 C.12 D. 1
?
B
C
3.下列各组数中互为相反数的是( )
A. - ( - 5 )与 -|- 5| B.|- 3|与|+3|
C. - ( - 1)与|- 1| D.|m|与|- m|
4.在 - 1,+ ( - 2 ),- ( - 3 ),- ( + 4 )中,负数有( )
A.1个 B.2个 C.3个 D.4个
A
C
5.(1)4 到原点的距离是 4 ,则 | 4 | = ______;
(2)-3 到原点的距离是 3 ,则 | -3 | = _______;
(3)0 到原点的距离是 0 ,则 | 0 |=_________.
6._______的相反数是它本身,_________的绝对值是它本身,___________的绝对值是它的相反数.
4
3
0
0
非负数
非正数
7.化简下列各数,并求出它们的绝对值.
(1)?(+10) (2)+(?0.15) (3)+(+3)
(4)?(?12) (5)+[?(?1.1)] (6)?[+(?7)]
?
解:(1)?(+10)=?10,|?(+10)|=10;
(2)+(?0.15)=?0.15,|+(?0.15)|=?0.15;
(3)+(+3)=3,|+(+3)|=3;
(4)?(?12)=12,|?(?12)|=12;
(5)+[?(?1.1)]=+(+1.1)=1.1,|+[?(?1.1)]|=1.1;
(6)?[+(?7)]=?(?7)=7,|?[+(?7)]|=7.
第一章 有理数
1.掌握绝对值的概念及其性质,能求一个有理数的绝对值;
2.理解相反数的含义和性质,会求一个数的相反数.
三位同学分别离学校多远?
0
1
2
3
4
-1
-2
-3
同学A
同学B
同学C
学校
单位:公里
表示4的点到原点的距离是4,
表示-2的点到原点的距离是2,
表示0的点到原点的距离是0.
活动1.画一条数轴,在数轴上标出表示4,-2,0的点,写出这些点到原点的距离.
探究一:绝对值的概念和意义.
在数轴上,表示一个数的点到原点的距离叫做这个数的绝对值,用“| |”表示.
思考:
1.0有没有绝对值?如果有,它的绝对值是多少?如果没有,说明为什么?
2.教材P12中提到的|a|表示什么含义,这样含义的点在数轴上有多少个?
3.如果????>0,|a|等于多少?????<0,????=0呢?
?
0
1
2
3
4
5
-1
-2
-3
-4
-5
结论1:
0的绝对值是0;
一个正数的绝对值是正数;
一个负数的绝对值是正数;
绝对值的性质
1.如图,点A表示的数的绝对值是( )
A.3 B.-3 C. D.
A
2.求下列各数的绝对值:
?53,7.5,?2.8,?34,+2
?
解:?53=53;7.5=7.5;?2.8=2.8;
?34=34;+2=2.
?
3
-3
1.5
-1.5
?16
?
16
?
①???3=3,?3=3
?
②???5=5,?5=5
?
③???16=16,?16=16
?
解:如图所示:
活动.用数轴上的点表示下列各组数,写出它们的绝对值,并完成后面的思考
?3,-3;?1.5,-1.5;? 16 ,?16 .
?
探究二:相反数的概念和意义.
思考1:这三组数在数轴上的位置有什么特点?它们的绝对值大小有什么关系?
思考2:如果将这种数组称称为其中的一个数是另一个数的相反数,那么用自己话说说,相反数的概念和特点.
像3和-3,5和-5这样,符号不同,绝对值相等的两个数,我们称其中一个数是另一个数的相反数,这两个数互为相反数.
思考3:0有相反数吗?如果有它的相反数是多少?如果没有,为什么?
0的相反数是0
注意:
1.互为相反数的两个数分别位于原点的两侧(0除外);互为相反数的两个数到原点的距离相等.
2.一般地,设a是一个正数,数轴上与原点的距离是a的点有两个,它们分别在原点的两侧,表示a和-a,这两点 关于原点对称.
3.表示一个数的相反数时,可以在这个数的前面添加一个“ - ”,因此,数 a 的相反数可以表示为 - a,这里 a 表示任意一个数,即它可以是正数、负数或者0.
结论1:0的绝对值是0;
一个正数的绝对值是正数;
一个负数的绝对值是正数.
绝对值的性质
结论2:0的绝对值是0;
一个正数的绝对值是正数;
一个负数的绝对值是它的相反数.
任何一个有理数的绝对值都是非负数.
1.完成下列问题,并说出你的发现:
①-(-3.5)表示______________; ∴-(-3.5)=______;
-(-a)表示______________; ∴-(-a)=______;
②-[-(-3.5)]表示_____________________; ∴-[-(-3.5)]=______;
-3.5的相反数
3.5
a的相反数
a
-3.5的相反数的相反数
-3.5
-a的相反数的相反数
-a
-[-(-a)]表示____________________; ∴-[-(-a)]=____.
结论:有理数a前面的“-”的个数为偶数时,结果为a;
有理数a前面的“-”的个数为奇数时,结果为-a.
有理数a前面的“-”的个数为偶数时,结果为a;
有理数a前面的“-”的个数为奇数时,结果为-a.
2.化简下列各数:
(1) -(- 3); (2) -(+ 2); (3) +(- 8);
(4) -[+(+ 2)]; (5) -{-[ -(+ ????)]} .
?
解:(1) -(-3)=3.
?
(2)-(+2)=-2.
?
(3)+(-8)=-8.
?
(4)-[+(+ 2)]=-(-2)=2.
?
(5)- {-[-(+????)]}=-[-(-????)]=-????.
?
绝对值与相反数
绝对值
相反数
几何意义
代数意义
在数轴上,表示数a到原点的距离.
|a|=a,(a>0)
|a|=-a,(a<0)
|a|=0,(a=0)
|a|≥0
几何意义
代数意义
符号不同,绝对值相等的两个数,互为相反数.
两个互为相反数的数在数轴上所表示的点在原点的两旁,且与原点的距离相等.
1.下列说法错误的是( )
A.-2的相反数是2 B.任何数的相反数都是负数
C.0的相反数是0 D.互为相反数的两个数相加等于0
2.?12的绝对值为( )
A.?2 B.?12 C.12 D. 1
?
B
C
3.下列各组数中互为相反数的是( )
A. - ( - 5 )与 -|- 5| B.|- 3|与|+3|
C. - ( - 1)与|- 1| D.|m|与|- m|
4.在 - 1,+ ( - 2 ),- ( - 3 ),- ( + 4 )中,负数有( )
A.1个 B.2个 C.3个 D.4个
A
C
5.(1)4 到原点的距离是 4 ,则 | 4 | = ______;
(2)-3 到原点的距离是 3 ,则 | -3 | = _______;
(3)0 到原点的距离是 0 ,则 | 0 |=_________.
6._______的相反数是它本身,_________的绝对值是它本身,___________的绝对值是它的相反数.
4
3
0
0
非负数
非正数
7.化简下列各数,并求出它们的绝对值.
(1)?(+10) (2)+(?0.15) (3)+(+3)
(4)?(?12) (5)+[?(?1.1)] (6)?[+(?7)]
?
解:(1)?(+10)=?10,|?(+10)|=10;
(2)+(?0.15)=?0.15,|+(?0.15)|=?0.15;
(3)+(+3)=3,|+(+3)|=3;
(4)?(?12)=12,|?(?12)|=12;
(5)+[?(?1.1)]=+(+1.1)=1.1,|+[?(?1.1)]|=1.1;
(6)?[+(?7)]=?(?7)=7,|?[+(?7)]|=7.
同课章节目录
- 第一章 有理数
- 1.1 正数和负数
- 1.2 数轴
- 1.3 绝对值与相反数
- 1.4 有理数的大小
- 1.5 有理数的加法
- 1.6 有理数的减法
- 1.7 有理数的加减混合运算
- 1.8 有理数的乘法
- 1.9 有理数的除法
- 1.10 有理数的乘方
- 1.11 有理数的混合运算
- 1.12 计算器的使用
- 第二章 几何图形的初步认识
- 2.1 从生活中认识几何图形
- 2.2 点和线
- 2.3 线段长短的比较
- 2.4 线段的和与差
- 2.5 角以及角的度量
- 2.6 角的大小
- 2.7 角的和与差
- 2.8 平面图形的旋转
- 第三章 代数式
- 3.1 用字母表示数
- 3.2 代数式
- 3.3 代数式的值
- 第四章 整式的加减
- 4.1 整式
- 4.2 合并同类项
- 4.3 去括号
- 4.4 整式的加减
- 第五章 一元一次方程
- 5.1一元一次方程
- 5.2 等式的基本性质
- 5.3 解一元一次方程
- 5.4 一元一次方程的应用
