1.4 有理数的大小 课件(共15张PPT) 2025-2026学年数学冀教版(2024)七年级上册
文档属性
| 名称 | 1.4 有理数的大小 课件(共15张PPT) 2025-2026学年数学冀教版(2024)七年级上册 |  | |
| 格式 | pptx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-25 06:07:07 | ||
图片预览





文档简介
1.4 有理数的大小
第一章 有理数
1.通过实例,掌握数轴比较有理数的大小的方法,能正确有理数的大小;
2.能根据绝对值的意义比较负有理数的大小,并能用其解释海拔的相关知识.
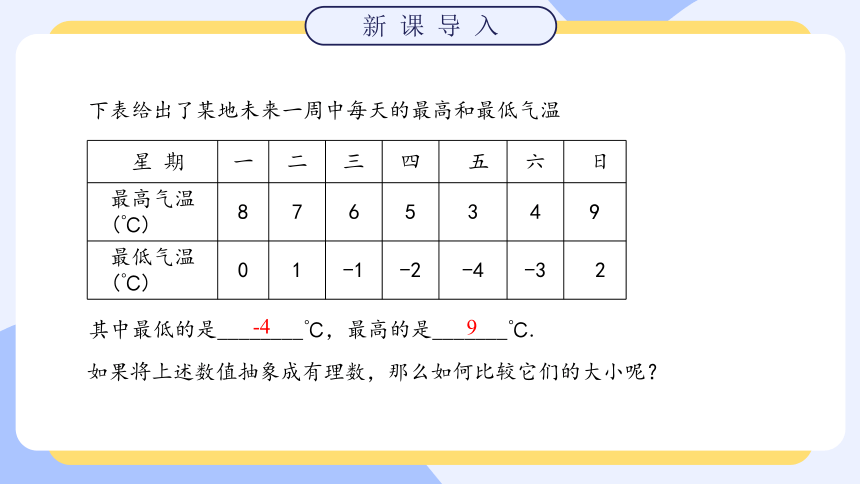
下表给出了某地未来一周中每天的最高和最低气温
{5940675A-B579-460E-94D1-54222C63F5DA} 星 期
一
二
三
四
五
六
日
最高气温(℃)
8
7
6
5
3
4
9
最低气温(℃)
0
1
-1
-2
-4
-3
2
其中最低的是________℃,最高的是_______℃.
如果将上述数值抽象成有理数,那么如何比较它们的大小呢?
-4
9
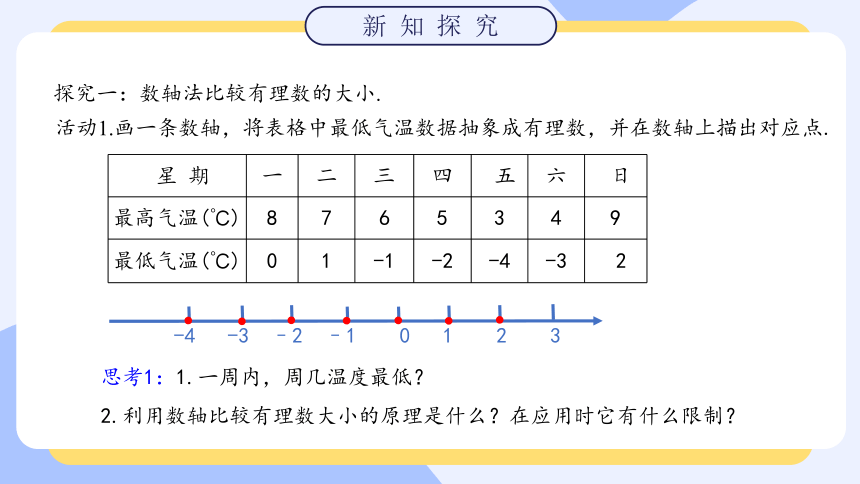
-4 -3 –2 –1 0 1 2 3
活动1.画一条数轴,将表格中最低气温数据抽象成有理数,并在数轴上描出对应点.
探究一:数轴法比较有理数的大小.
{5940675A-B579-460E-94D1-54222C63F5DA} 星 期
一
二
三
四
五
六
日
最高气温(℃)
8
7
6
5
3
4
9
最低气温(℃)
0
1
-1
-2
-4
-3
2
思考1:1.一周内,周几温度最低?
2.利用数轴比较有理数大小的原理是什么?在应用时它有什么限制?
注意:
1.数轴比较法适用于多个数的大小比较;
2.对于一些较大的数,在数轴上不好描点,因此不适用于数轴比较法.
1.在数轴上表示的两个数,右边的数总比左边的数大.
2.正数大于0,0大于负数,正数大于负数.
请在数轴上表示下列各数,并按从小到大的顺序用“<” 连接起来:
?2, 0, 1, ?0.5, ?32 , 212 .
?
解:将这些数在数轴上表示出来,如图.
所以?2?
思考2:它们的大小与其绝对值有什么关系?
1
0
2
3
4
5
6
7
-1
-2
-3
8
1<2<3<4
正数的绝对值越大,在数轴上越靠右
即:两个正数,绝对值大的数大
活动1.画一条数轴,利用数轴比较1,2,3,4的大小.
探究二:绝对值的性质法比较有理数的大小.
1
0
2
3
4
5
6
7
-1
-2
-3
8
-1>-2>-3
负数的绝对值越大,在数轴上越靠左,则这个负数越小
即:两个负数,绝对值大的数小
活动2.画一条数轴,利用数轴比较-1,-2,-3的大小.
思考3:它们的大小与其绝对值有什么关系?
讨论:根据思考2和思考3,用绝对值可以比较哪类有理数的大小?如何比较?
绝对值比较两个负数大小:
两个负数,绝对值大的反而小.
思考4:阅读教材P17中的“大家谈谈”,说说你对这两个结论的理解?
1.0:平均海平面,正数:高度高于平均海平面,负数:高度低于平均海平面;
2.当海拔低于平均海平面时,如果海拔越低,意味着其离平均海平面越远;
比较下列各组数的大小:
(1)2和?1.4;?;(2) ?|?5| 和 0; (3)?45和?34 .
?
解:(1)2>?1.4(正数>负数).
(2)因为?|?5|=?5,且?5<0,所以?|?5|<0.
(3)因为|?45|=45=1620,|?34|=34=1520,且1620>1520, 所以?45>?34.
?
注意:结果要落到原数上.
比较有理数的大小时,应抓住两点:
1.识别数的正负性,直接利用“正数>0>负数”进行比较;
?
2.两个负数相比较,先比较其绝对值,再根据绝对值大的反而小的原则进行比较.
比较有理数的大小
利用数轴比较大小
利用法则比较大小
在数轴上表示的两个数,右边的数总比左边的数大.
正数大于0,负数小于0,
正数大于负数.
两个负数,绝对值大的反而小
1.下面有理数比较大小正确的是( )
A.0?
B
2.下列选项中,比- 5小的数是( ? ? )
A. -4 B. 0 C. 12 D. -6
?
D
3.下列4个地方,死海(海拔-400米),卡达拉低地(海拔-133米),罗讷河三角洲(海拔-2米),吐鲁番盆地(海拔-154米),其中最低的地方是_________________.
死海
4.比较大小
(1)|?2.1| ?(?2.1) (2) ?(?4 ) ?|?4.5|
(3) +(?156) ? (+157)
?
=
?
>
?
<
?
5.下列判断,正确的是( )
A.若????>????,则│????│>│????│
B.若│????│>│????│,则????>????
C.若????<????<0,则│????│<│????│
D.若????>????>0,则│????│>│????│
?
????
?
如????=1,????=?2
?
如????=?3,????=2
?
如????=?3,????=?2
第一章 有理数
1.通过实例,掌握数轴比较有理数的大小的方法,能正确有理数的大小;
2.能根据绝对值的意义比较负有理数的大小,并能用其解释海拔的相关知识.
下表给出了某地未来一周中每天的最高和最低气温
{5940675A-B579-460E-94D1-54222C63F5DA} 星 期
一
二
三
四
五
六
日
最高气温(℃)
8
7
6
5
3
4
9
最低气温(℃)
0
1
-1
-2
-4
-3
2
其中最低的是________℃,最高的是_______℃.
如果将上述数值抽象成有理数,那么如何比较它们的大小呢?
-4
9
-4 -3 –2 –1 0 1 2 3
活动1.画一条数轴,将表格中最低气温数据抽象成有理数,并在数轴上描出对应点.
探究一:数轴法比较有理数的大小.
{5940675A-B579-460E-94D1-54222C63F5DA} 星 期
一
二
三
四
五
六
日
最高气温(℃)
8
7
6
5
3
4
9
最低气温(℃)
0
1
-1
-2
-4
-3
2
思考1:1.一周内,周几温度最低?
2.利用数轴比较有理数大小的原理是什么?在应用时它有什么限制?
注意:
1.数轴比较法适用于多个数的大小比较;
2.对于一些较大的数,在数轴上不好描点,因此不适用于数轴比较法.
1.在数轴上表示的两个数,右边的数总比左边的数大.
2.正数大于0,0大于负数,正数大于负数.
请在数轴上表示下列各数,并按从小到大的顺序用“<” 连接起来:
?2, 0, 1, ?0.5, ?32 , 212 .
?
解:将这些数在数轴上表示出来,如图.
所以?2?
思考2:它们的大小与其绝对值有什么关系?
1
0
2
3
4
5
6
7
-1
-2
-3
8
1<2<3<4
正数的绝对值越大,在数轴上越靠右
即:两个正数,绝对值大的数大
活动1.画一条数轴,利用数轴比较1,2,3,4的大小.
探究二:绝对值的性质法比较有理数的大小.
1
0
2
3
4
5
6
7
-1
-2
-3
8
-1>-2>-3
负数的绝对值越大,在数轴上越靠左,则这个负数越小
即:两个负数,绝对值大的数小
活动2.画一条数轴,利用数轴比较-1,-2,-3的大小.
思考3:它们的大小与其绝对值有什么关系?
讨论:根据思考2和思考3,用绝对值可以比较哪类有理数的大小?如何比较?
绝对值比较两个负数大小:
两个负数,绝对值大的反而小.
思考4:阅读教材P17中的“大家谈谈”,说说你对这两个结论的理解?
1.0:平均海平面,正数:高度高于平均海平面,负数:高度低于平均海平面;
2.当海拔低于平均海平面时,如果海拔越低,意味着其离平均海平面越远;
比较下列各组数的大小:
(1)2和?1.4;?;(2) ?|?5| 和 0; (3)?45和?34 .
?
解:(1)2>?1.4(正数>负数).
(2)因为?|?5|=?5,且?5<0,所以?|?5|<0.
(3)因为|?45|=45=1620,|?34|=34=1520,且1620>1520, 所以?45>?34.
?
注意:结果要落到原数上.
比较有理数的大小时,应抓住两点:
1.识别数的正负性,直接利用“正数>0>负数”进行比较;
?
2.两个负数相比较,先比较其绝对值,再根据绝对值大的反而小的原则进行比较.
比较有理数的大小
利用数轴比较大小
利用法则比较大小
在数轴上表示的两个数,右边的数总比左边的数大.
正数大于0,负数小于0,
正数大于负数.
两个负数,绝对值大的反而小
1.下面有理数比较大小正确的是( )
A.0?
B
2.下列选项中,比- 5小的数是( ? ? )
A. -4 B. 0 C. 12 D. -6
?
D
3.下列4个地方,死海(海拔-400米),卡达拉低地(海拔-133米),罗讷河三角洲(海拔-2米),吐鲁番盆地(海拔-154米),其中最低的地方是_________________.
死海
4.比较大小
(1)|?2.1| ?(?2.1) (2) ?(?4 ) ?|?4.5|
(3) +(?156) ? (+157)
?
=
?
>
?
<
?
5.下列判断,正确的是( )
A.若????>????,则│????│>│????│
B.若│????│>│????│,则????>????
C.若????<????<0,则│????│<│????│
D.若????>????>0,则│????│>│????│
?
????
?
如????=1,????=?2
?
如????=?3,????=2
?
如????=?3,????=?2
同课章节目录
- 第一章 有理数
- 1.1 正数和负数
- 1.2 数轴
- 1.3 绝对值与相反数
- 1.4 有理数的大小
- 1.5 有理数的加法
- 1.6 有理数的减法
- 1.7 有理数的加减混合运算
- 1.8 有理数的乘法
- 1.9 有理数的除法
- 1.10 有理数的乘方
- 1.11 有理数的混合运算
- 1.12 计算器的使用
- 第二章 几何图形的初步认识
- 2.1 从生活中认识几何图形
- 2.2 点和线
- 2.3 线段长短的比较
- 2.4 线段的和与差
- 2.5 角以及角的度量
- 2.6 角的大小
- 2.7 角的和与差
- 2.8 平面图形的旋转
- 第三章 代数式
- 3.1 用字母表示数
- 3.2 代数式
- 3.3 代数式的值
- 第四章 整式的加减
- 4.1 整式
- 4.2 合并同类项
- 4.3 去括号
- 4.4 整式的加减
- 第五章 一元一次方程
- 5.1一元一次方程
- 5.2 等式的基本性质
- 5.3 解一元一次方程
- 5.4 一元一次方程的应用
