2.3 线段长短的比较 课件(共15张PPT)2025-2026学年数学冀教版(2024)七年级上册
文档属性
| 名称 | 2.3 线段长短的比较 课件(共15张PPT)2025-2026学年数学冀教版(2024)七年级上册 |  | |
| 格式 | pptx | ||
| 文件大小 | 504.8KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-25 06:46:39 | ||
图片预览





文档简介
(共15张PPT)
2.3 线段长短的比较
第二章 几何图形的初步认识
1. 能从日常“比身高”的方法中抽象出叠合法,掌握线段长短比较的不同方法,并能正确比较线段的长短;
2.掌握“两点之间,线段最短”的基本事实,并能用来解决实际问题.
位于线段AB两端的点A,B,叫作这条线段的端点.
将线段AB沿AB方向(或BA方向)无限延伸所形成的图形,叫作射线.
将线段AB沿这条线段向两方无限延伸所形成的图形,叫作直线.
基本事实 两点确定一条直线.
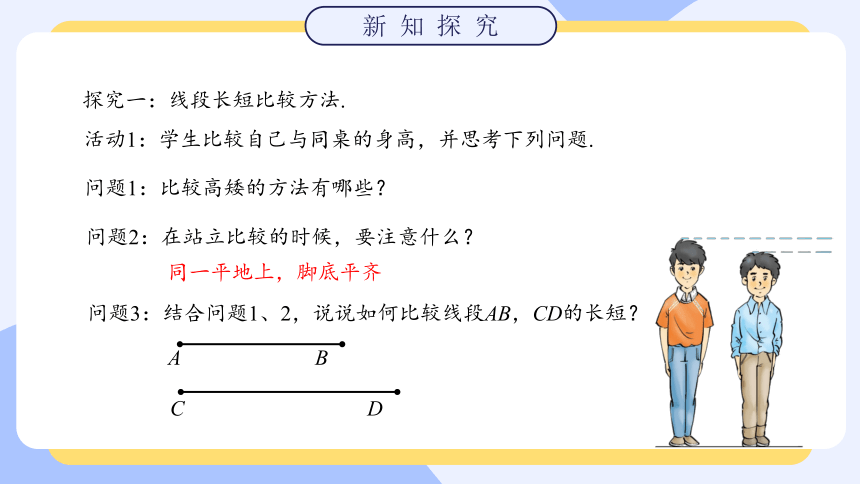
问题1:比较高矮的方法有哪些?
探究一:线段长短比较方法.
活动1:学生比较自己与同桌的身高,并思考下列问题.
问题2:在站立比较的时候,要注意什么?
问题3:结合问题1、2,说说如何比较线段AB,CD的长短?
同一平地上,脚底平齐
C D
A B
探究一:线段长短比较方法.
活动2:用叠合法比较线段AB,CD的长短,并归纳叠合法的步骤.
C D
A B
(1)两条线段在同一条直线上;
(2)线段左端点重合;
(3)观察线段又端点的位置.
思考:将线段线段叠合上,那么和时点的位置有什么变化?
线段长度比较方法:
(1) 度量法:即用刻度尺分别量出AB,CD的长度,长度大的线段较长,长度小的线段较短;长度相等时,两条线段相等.
(2) 叠合法:将线段AB放到线段CD上,使点A与点C重合,点B与点D落在点A(也是点C)的同侧.
C D
A B
C
D
(A)
B
<
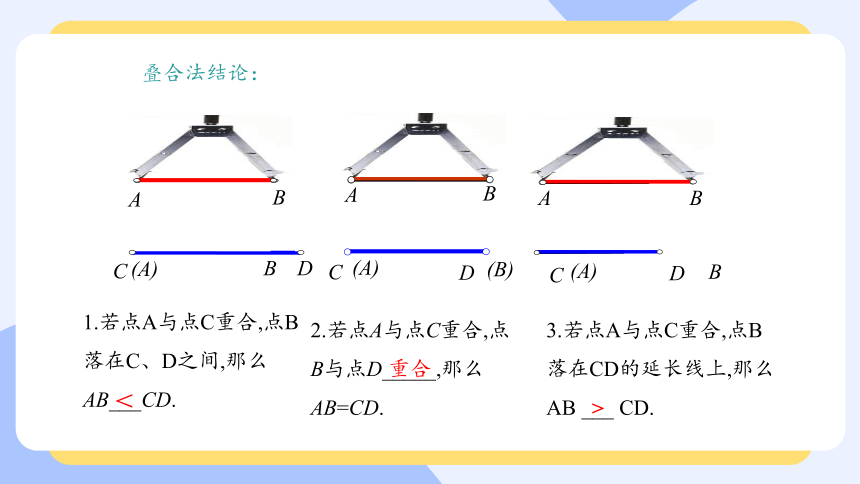
叠合法结论:
B
A
C
(B)
(A)
D
A
B
C
D
B
(A)
B
A
1.若点A与点C重合,点B落在C、D之间,那么AB___CD.
2.若点A与点C重合,点B与点D_____,那么AB=CD.
3.若点A与点C重合,点B落在CD的延长线上,那么AB ___ CD.
重合
>
思考:除了度量法、和叠合法比较外,还有什么其他方法比较线段AB,CD的长短?
C D
A B
尺规作图:(1)用圆规截取线段AB的长;
(2)点A与圆规的一端重合,另一端在射
线AD上画弧,观察B点的位置.
①把圆规的两脚尖分别放在点A,B上.
作法:
②移动圆规,使圆规的一个脚尖与点C重合,另一个脚尖在线段CD上截取的点记为B'.
1.下列图形中能比较大小的是( )
A.两条线段 B.两条直线
C.直线与射线 D.两条射线
2.比较线段a和b的大小,其结果一定是( )
A.a=b B.a>b
C.a<b D.a>b或a=b或a<b
D
A
如图:从 A 地到 B 地有四条路线可走,甲、乙、丙、丁分别骑自行车从A地出发,沿不同的路线去B地,谁走的路最短?
探究二.两点之间,线段最短.
活动1:阅读材料,选择合适的路径.
思考:在连接两点间的各类线中,怎样的线最短?
线段的基本事实:
两点之间,线段最短.
两点之间的距离:
两点之间线段的长度
注意:两点间的距离是指连接两点间的线段的长度,如 A,B 两点的距离是指线段AB 的长度,而不是线段 AB 本身.
如图所示,某同学的家在A处,书店在B处,星期日他到书店去买书,想尽快赶到书店,请你帮助他选择一条最近的路线( )
A.A→C→D→B
B.A→C→F→B
C.A→C→E→F→B
D.A→C→M→B
B
线段比较方法:度量法、叠合法
关于线段的基本事实:
两点之间,线段最短.
两点的距离:
两点之间线段的长度,叫作两点之间的距离.
1.如图,AB=CD,可得AC与BD的大小关系是( )
A.AC>BD B.AC<BD
C.AC=BD D.不能确定
2.如图,点A,B在直线l上,点C是直线l外一点,可知CA+CB>AB,其依据是( )
A.两点之间,线段最短 B.两点确定一条直线
C.两点之间,直线最短 D.直线比线段长
C
A
3.如图,公园里修建了曲折迂回的桥,这与修一座直的桥相比,对游人观赏湖面风光能起到什么作用?用你所学数学知识说明其中的道理.
由于“两点之间,线段最短”,这样做增加桥的长度,一方面使这座桥能容纳更多的游人来观光,另一方面也增加了游人在桥上行走的路程,有利于游人更好地观赏湖面风光.
2.3 线段长短的比较
第二章 几何图形的初步认识
1. 能从日常“比身高”的方法中抽象出叠合法,掌握线段长短比较的不同方法,并能正确比较线段的长短;
2.掌握“两点之间,线段最短”的基本事实,并能用来解决实际问题.
位于线段AB两端的点A,B,叫作这条线段的端点.
将线段AB沿AB方向(或BA方向)无限延伸所形成的图形,叫作射线.
将线段AB沿这条线段向两方无限延伸所形成的图形,叫作直线.
基本事实 两点确定一条直线.
问题1:比较高矮的方法有哪些?
探究一:线段长短比较方法.
活动1:学生比较自己与同桌的身高,并思考下列问题.
问题2:在站立比较的时候,要注意什么?
问题3:结合问题1、2,说说如何比较线段AB,CD的长短?
同一平地上,脚底平齐
C D
A B
探究一:线段长短比较方法.
活动2:用叠合法比较线段AB,CD的长短,并归纳叠合法的步骤.
C D
A B
(1)两条线段在同一条直线上;
(2)线段左端点重合;
(3)观察线段又端点的位置.
思考:将线段线段叠合上,那么和时点的位置有什么变化?
线段长度比较方法:
(1) 度量法:即用刻度尺分别量出AB,CD的长度,长度大的线段较长,长度小的线段较短;长度相等时,两条线段相等.
(2) 叠合法:将线段AB放到线段CD上,使点A与点C重合,点B与点D落在点A(也是点C)的同侧.
C D
A B
C
D
(A)
B
<
叠合法结论:
B
A
C
(B)
(A)
D
A
B
C
D
B
(A)
B
A
1.若点A与点C重合,点B落在C、D之间,那么AB___CD.
2.若点A与点C重合,点B与点D_____,那么AB=CD.
3.若点A与点C重合,点B落在CD的延长线上,那么AB ___ CD.
重合
>
思考:除了度量法、和叠合法比较外,还有什么其他方法比较线段AB,CD的长短?
C D
A B
尺规作图:(1)用圆规截取线段AB的长;
(2)点A与圆规的一端重合,另一端在射
线AD上画弧,观察B点的位置.
①把圆规的两脚尖分别放在点A,B上.
作法:
②移动圆规,使圆规的一个脚尖与点C重合,另一个脚尖在线段CD上截取的点记为B'.
1.下列图形中能比较大小的是( )
A.两条线段 B.两条直线
C.直线与射线 D.两条射线
2.比较线段a和b的大小,其结果一定是( )
A.a=b B.a>b
C.a<b D.a>b或a=b或a<b
D
A
如图:从 A 地到 B 地有四条路线可走,甲、乙、丙、丁分别骑自行车从A地出发,沿不同的路线去B地,谁走的路最短?
探究二.两点之间,线段最短.
活动1:阅读材料,选择合适的路径.
思考:在连接两点间的各类线中,怎样的线最短?
线段的基本事实:
两点之间,线段最短.
两点之间的距离:
两点之间线段的长度
注意:两点间的距离是指连接两点间的线段的长度,如 A,B 两点的距离是指线段AB 的长度,而不是线段 AB 本身.
如图所示,某同学的家在A处,书店在B处,星期日他到书店去买书,想尽快赶到书店,请你帮助他选择一条最近的路线( )
A.A→C→D→B
B.A→C→F→B
C.A→C→E→F→B
D.A→C→M→B
B
线段比较方法:度量法、叠合法
关于线段的基本事实:
两点之间,线段最短.
两点的距离:
两点之间线段的长度,叫作两点之间的距离.
1.如图,AB=CD,可得AC与BD的大小关系是( )
A.AC>BD B.AC<BD
C.AC=BD D.不能确定
2.如图,点A,B在直线l上,点C是直线l外一点,可知CA+CB>AB,其依据是( )
A.两点之间,线段最短 B.两点确定一条直线
C.两点之间,直线最短 D.直线比线段长
C
A
3.如图,公园里修建了曲折迂回的桥,这与修一座直的桥相比,对游人观赏湖面风光能起到什么作用?用你所学数学知识说明其中的道理.
由于“两点之间,线段最短”,这样做增加桥的长度,一方面使这座桥能容纳更多的游人来观光,另一方面也增加了游人在桥上行走的路程,有利于游人更好地观赏湖面风光.
同课章节目录
- 第一章 有理数
- 1.1 正数和负数
- 1.2 数轴
- 1.3 绝对值与相反数
- 1.4 有理数的大小
- 1.5 有理数的加法
- 1.6 有理数的减法
- 1.7 有理数的加减混合运算
- 1.8 有理数的乘法
- 1.9 有理数的除法
- 1.10 有理数的乘方
- 1.11 有理数的混合运算
- 1.12 计算器的使用
- 第二章 几何图形的初步认识
- 2.1 从生活中认识几何图形
- 2.2 点和线
- 2.3 线段长短的比较
- 2.4 线段的和与差
- 2.5 角以及角的度量
- 2.6 角的大小
- 2.7 角的和与差
- 2.8 平面图形的旋转
- 第三章 代数式
- 3.1 用字母表示数
- 3.2 代数式
- 3.3 代数式的值
- 第四章 整式的加减
- 4.1 整式
- 4.2 合并同类项
- 4.3 去括号
- 4.4 整式的加减
- 第五章 一元一次方程
- 5.1一元一次方程
- 5.2 等式的基本性质
- 5.3 解一元一次方程
- 5.4 一元一次方程的应用
