2.8 平面图形的旋转 课件(共16张PPT)2025-2026学年数学冀教版(2024)七年级上册
文档属性
| 名称 | 2.8 平面图形的旋转 课件(共16张PPT)2025-2026学年数学冀教版(2024)七年级上册 |  | |
| 格式 | pptx | ||
| 文件大小 | 904.8KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-25 06:44:19 | ||
图片预览




文档简介
(共16张PPT)
2.8 平面图形的旋转
第二章 几何图形的初步认识
1. 通过对显示现象的抽象,认识旋转运动,掌握其相关概念;
2. 理解旋转的性质,能根据旋转性质作出简单平面图形旋转后的图形.
观察下面图形,钟表的指针和风力发电机的叶片在做什么样的运动?
这种运动在数学上是怎么定义的,有什么特点,如何绘制运动后的图形?
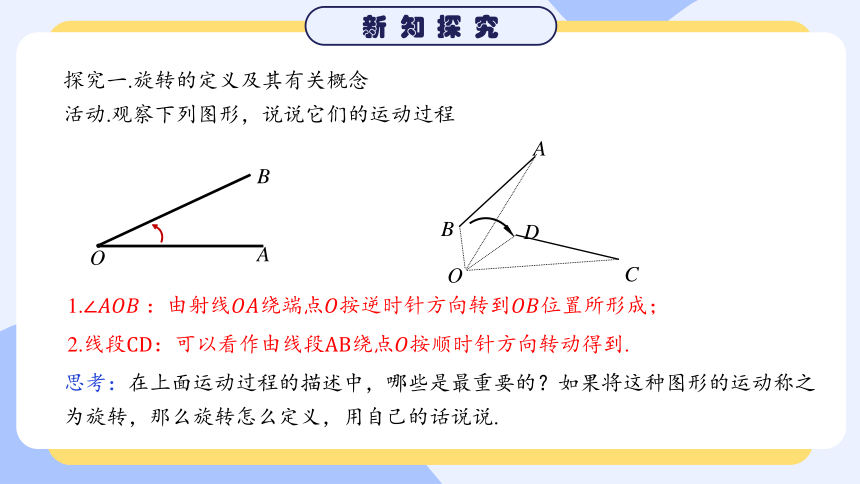
1.:由射线绕端点按逆时针方向转到位置所形成;
2.线段:可以看作由线段绕点按顺时针方向转动得到.
O
A
B
探究一.旋转的定义及其有关概念
活动.观察下列图形,说说它们的运动过程
A
B
D
C
O
思考:在上面运动过程的描述中,哪些是最重要的?如果将这种图形的运动称之为旋转,那么旋转怎么定义,用自己的话说说.
在平面内,一个图形绕一个定点沿顺时针(或逆时针)方向转过一个角度,这样的图形运动叫作旋转.这个定点叫作旋转中心,转过的这个角叫作旋转角.
旋转中心、旋转方向、旋转角是旋转的三要素.
O
A
B
A
B
D
C
O
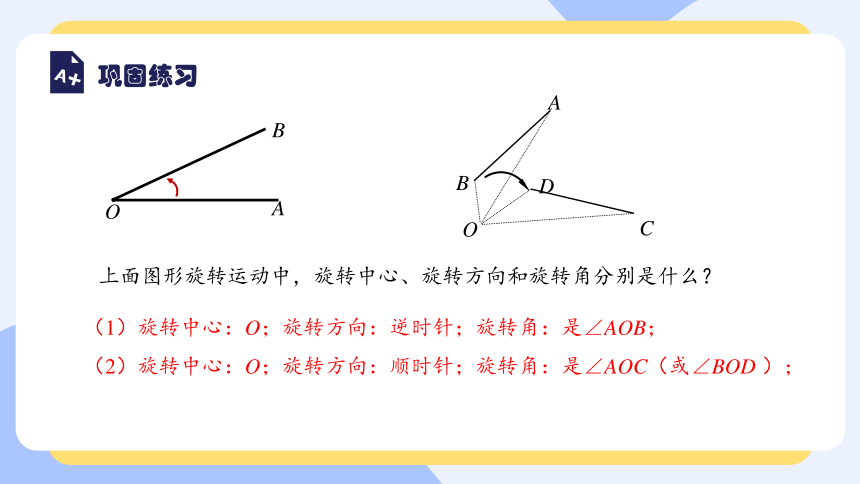
上面图形旋转运动中,旋转中心、旋转方向和旋转角分别是什么?
(1)旋转中心:O;旋转方向:逆时针;旋转角:是∠AOB;
(2)旋转中心:O;旋转方向:顺时针;旋转角:是∠AOC(或∠BOD );
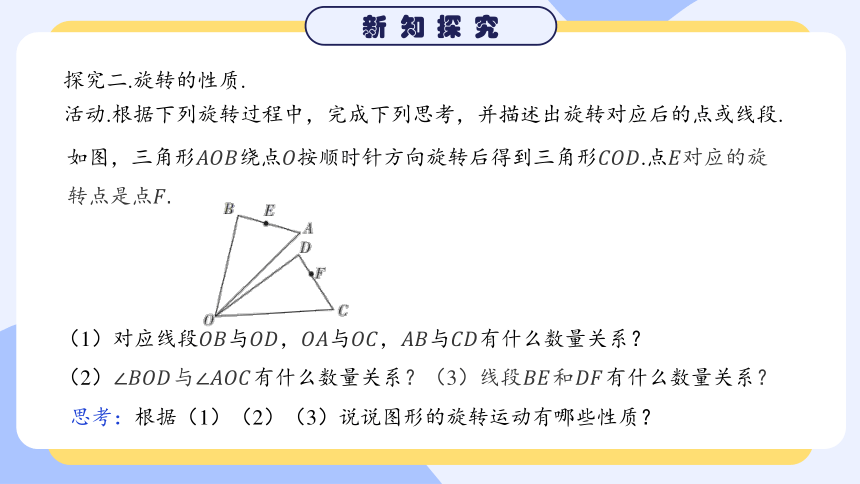
探究二.旋转的性质.
活动.根据下列旋转过程中,完成下列思考,并描述出旋转对应后的点或线段.
如图,三角形绕点按顺时针方向旋转后得到三角形.点对应的旋转点是点.
(1)对应线段与,与,与有什么数量关系?
(2)与有什么数量关系?(3)线段和有什么数量关系?
思考:根据(1)(2)(3)说说图形的旋转运动有哪些性质?
图形旋转运动的性质:
1.对应点到旋转中心的距离相等;
2.两组对应点分别与旋转中心连线所成的角相等,都等于旋转角;
3.旋转只改变图形的位置,不改变图形的形状和大小.
如图,将△ABO绕点O旋转得到
△ CDO,若AB=2,OA=4,OB=3,∠A=40°,则下列说法:①点B的对应点是点D;②OD=2;③OC=4;④∠C=40°;⑤旋转中心是点O;⑥旋转角为40°.其中正确的是 ( )
A.①③④⑤ B.①②③⑤
C.③④⑤⑥ D.①②③④⑤⑥
A
探究三.旋转作图的条件和步骤.
活动.阅读教材P91的例题,小组讨论下列问题.
1.要进行旋转作图,它需要知道哪些条件?
2.根据例题的解答过程,总结抽象出对于一般图形,它的作图步骤是怎样的?
2.(1)确定旋转中心及旋转方向、旋转角;(2)找出原图形的关键点;
(3)将原图形的各关键点与旋转中心分别连接起来,根据旋转方向与旋转角度,以各关键点与旋转中心的连线为一边作旋转角,在各旋转角的另一边上,从旋转中心开始截取各关键点到旋转中心的长度,得到这些关键点的对应点;
(4)按原图形的顺序连接这些对应点,所得到的图形就是旋转后的图形.
1.①已知图形;②旋转中心;③旋转方向和旋转角.
1.旋转作图的条件
①已知图形;②旋转中心;③旋转方向和旋转角.
2.旋转作图的步骤
(1)确定旋转三要素:旋转中心及旋转方向、旋转角;
(2)确定关键点(原图形);
(3)连线(关键点与旋转中心);
(4)作旋转角,得旋转角的另一边
(5)定对应点(从旋转中心开始截取各关键点到旋转中心的长度)
(6)连点成线(按原图形的顺序连接这些对应点)
1.图1的方格纸上有一面“小旗子”画出小旗子绕点A按逆时针方向旋转90°后的图案;
2.画出图2中的图形绕点B按顺时针方向旋转60°后的图形.
图1
图2
平面图形的旋转
旋转的定义
旋转的性质
在平面内,一个图形绕一个定点沿顺时针(或逆时针)方向转过一个角度,这样的图形运动叫作旋转. 这个定点叫作旋转中心,转过的这个角叫作旋转角.
1.旋转只改变图形的位置,不改变图形的形状和大小.
2.对应点到旋转中心的距离相等
3.两组对应点分别与旋转中心连线所成的角相等,它们都等于旋转角,
1.下列现象中,属于旋转的是( )
A.钟摆的摆动 B.飞机在飞行
C.汽车在奔驰 D.小鸟飞翔
A
2.如图,在等腰直角三角形ABC中,∠B=90°,将三角形ABC绕顶点A按
逆时针方向旋转60°后得到三角形AB′C′,则∠BAC′等于( )
A.60° B.105° C.120° D.135°
B
3.如图,三角形ABC按顺时针方向旋转到三角形ADE的位置,以下关于旋转中心和对应点的说法正确的是( )
A.点A是旋转中心,点B和点E是对应点
B.点C是旋转中心,点B和点D是对应点
C.点A是旋转中心,点C和点E是对应点
D.点D是旋转中心,点A和点D是对应点
C
7.将等边三角形CBA绕点C顺时针旋转∠α得到三角形CB′A′,使得B,C,A′
三点在同一直线上,如图所示,则∠α的大小是___________.
120°
2.8 平面图形的旋转
第二章 几何图形的初步认识
1. 通过对显示现象的抽象,认识旋转运动,掌握其相关概念;
2. 理解旋转的性质,能根据旋转性质作出简单平面图形旋转后的图形.
观察下面图形,钟表的指针和风力发电机的叶片在做什么样的运动?
这种运动在数学上是怎么定义的,有什么特点,如何绘制运动后的图形?
1.:由射线绕端点按逆时针方向转到位置所形成;
2.线段:可以看作由线段绕点按顺时针方向转动得到.
O
A
B
探究一.旋转的定义及其有关概念
活动.观察下列图形,说说它们的运动过程
A
B
D
C
O
思考:在上面运动过程的描述中,哪些是最重要的?如果将这种图形的运动称之为旋转,那么旋转怎么定义,用自己的话说说.
在平面内,一个图形绕一个定点沿顺时针(或逆时针)方向转过一个角度,这样的图形运动叫作旋转.这个定点叫作旋转中心,转过的这个角叫作旋转角.
旋转中心、旋转方向、旋转角是旋转的三要素.
O
A
B
A
B
D
C
O
上面图形旋转运动中,旋转中心、旋转方向和旋转角分别是什么?
(1)旋转中心:O;旋转方向:逆时针;旋转角:是∠AOB;
(2)旋转中心:O;旋转方向:顺时针;旋转角:是∠AOC(或∠BOD );
探究二.旋转的性质.
活动.根据下列旋转过程中,完成下列思考,并描述出旋转对应后的点或线段.
如图,三角形绕点按顺时针方向旋转后得到三角形.点对应的旋转点是点.
(1)对应线段与,与,与有什么数量关系?
(2)与有什么数量关系?(3)线段和有什么数量关系?
思考:根据(1)(2)(3)说说图形的旋转运动有哪些性质?
图形旋转运动的性质:
1.对应点到旋转中心的距离相等;
2.两组对应点分别与旋转中心连线所成的角相等,都等于旋转角;
3.旋转只改变图形的位置,不改变图形的形状和大小.
如图,将△ABO绕点O旋转得到
△ CDO,若AB=2,OA=4,OB=3,∠A=40°,则下列说法:①点B的对应点是点D;②OD=2;③OC=4;④∠C=40°;⑤旋转中心是点O;⑥旋转角为40°.其中正确的是 ( )
A.①③④⑤ B.①②③⑤
C.③④⑤⑥ D.①②③④⑤⑥
A
探究三.旋转作图的条件和步骤.
活动.阅读教材P91的例题,小组讨论下列问题.
1.要进行旋转作图,它需要知道哪些条件?
2.根据例题的解答过程,总结抽象出对于一般图形,它的作图步骤是怎样的?
2.(1)确定旋转中心及旋转方向、旋转角;(2)找出原图形的关键点;
(3)将原图形的各关键点与旋转中心分别连接起来,根据旋转方向与旋转角度,以各关键点与旋转中心的连线为一边作旋转角,在各旋转角的另一边上,从旋转中心开始截取各关键点到旋转中心的长度,得到这些关键点的对应点;
(4)按原图形的顺序连接这些对应点,所得到的图形就是旋转后的图形.
1.①已知图形;②旋转中心;③旋转方向和旋转角.
1.旋转作图的条件
①已知图形;②旋转中心;③旋转方向和旋转角.
2.旋转作图的步骤
(1)确定旋转三要素:旋转中心及旋转方向、旋转角;
(2)确定关键点(原图形);
(3)连线(关键点与旋转中心);
(4)作旋转角,得旋转角的另一边
(5)定对应点(从旋转中心开始截取各关键点到旋转中心的长度)
(6)连点成线(按原图形的顺序连接这些对应点)
1.图1的方格纸上有一面“小旗子”画出小旗子绕点A按逆时针方向旋转90°后的图案;
2.画出图2中的图形绕点B按顺时针方向旋转60°后的图形.
图1
图2
平面图形的旋转
旋转的定义
旋转的性质
在平面内,一个图形绕一个定点沿顺时针(或逆时针)方向转过一个角度,这样的图形运动叫作旋转. 这个定点叫作旋转中心,转过的这个角叫作旋转角.
1.旋转只改变图形的位置,不改变图形的形状和大小.
2.对应点到旋转中心的距离相等
3.两组对应点分别与旋转中心连线所成的角相等,它们都等于旋转角,
1.下列现象中,属于旋转的是( )
A.钟摆的摆动 B.飞机在飞行
C.汽车在奔驰 D.小鸟飞翔
A
2.如图,在等腰直角三角形ABC中,∠B=90°,将三角形ABC绕顶点A按
逆时针方向旋转60°后得到三角形AB′C′,则∠BAC′等于( )
A.60° B.105° C.120° D.135°
B
3.如图,三角形ABC按顺时针方向旋转到三角形ADE的位置,以下关于旋转中心和对应点的说法正确的是( )
A.点A是旋转中心,点B和点E是对应点
B.点C是旋转中心,点B和点D是对应点
C.点A是旋转中心,点C和点E是对应点
D.点D是旋转中心,点A和点D是对应点
C
7.将等边三角形CBA绕点C顺时针旋转∠α得到三角形CB′A′,使得B,C,A′
三点在同一直线上,如图所示,则∠α的大小是___________.
120°
同课章节目录
- 第一章 有理数
- 1.1 正数和负数
- 1.2 数轴
- 1.3 绝对值与相反数
- 1.4 有理数的大小
- 1.5 有理数的加法
- 1.6 有理数的减法
- 1.7 有理数的加减混合运算
- 1.8 有理数的乘法
- 1.9 有理数的除法
- 1.10 有理数的乘方
- 1.11 有理数的混合运算
- 1.12 计算器的使用
- 第二章 几何图形的初步认识
- 2.1 从生活中认识几何图形
- 2.2 点和线
- 2.3 线段长短的比较
- 2.4 线段的和与差
- 2.5 角以及角的度量
- 2.6 角的大小
- 2.7 角的和与差
- 2.8 平面图形的旋转
- 第三章 代数式
- 3.1 用字母表示数
- 3.2 代数式
- 3.3 代数式的值
- 第四章 整式的加减
- 4.1 整式
- 4.2 合并同类项
- 4.3 去括号
- 4.4 整式的加减
- 第五章 一元一次方程
- 5.1一元一次方程
- 5.2 等式的基本性质
- 5.3 解一元一次方程
- 5.4 一元一次方程的应用
