3.4 代数式的值 课时1 求代数式的值 课件(共33张PPT)2025-2026学年数学冀教版(2024)七年级上册
文档属性
| 名称 | 3.4 代数式的值 课时1 求代数式的值 课件(共33张PPT)2025-2026学年数学冀教版(2024)七年级上册 |  | |
| 格式 | pptx | ||
| 文件大小 | 834.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-25 06:58:40 | ||
图片预览










文档简介
3.4 代数式的值
第三章 代数式
3.4 课时1 求代数式的值
第三章 代数式
1.理解代数式的值的概念,会求代数式的值,提高运算能力.
2.通过求代数式的值,体会代数式实际上是由计算程序
反映的一种数量关系.
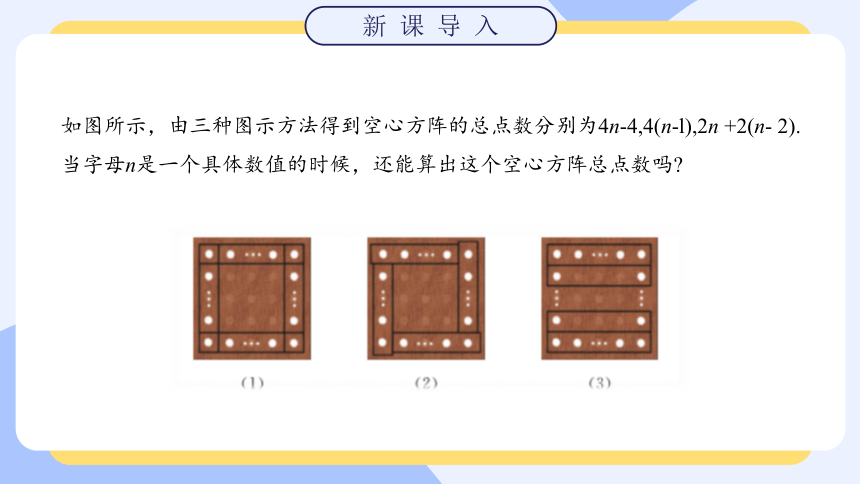
如图所示,由三种图示方法得到空心方阵的总点数分别为4n-4,4(n-l),2n +2(n- 2).当字母n是一个具体数值的时候,还能算出这个空心方阵总点数吗?
...
...
...
...
n个点
n个点
4n-4
探究一.代数式的值的概念
活动1.分析下列问题,同桌讨论代数式的值的概念.
(1)当n取4, 10, 15,25等值时,分别代入上面的代数式,计算出代数式的值,并思考,对于n的同一个值,同学们得到的结果都一样吗?
(2)根据(1)中n的取值,如何计算出4n-4的值呢?
当????=4时,4????-4=4×4?4=12;
当????=10时,4????-4=4×10?4=36;
当????=15时,4????-4=4×15?4=56;
当????=4时,4????-4=4×25?4=96;
?
对代数式中的字母代入不同的值,都可以求出代数式相应的值.一个代数式,可以看做一个计算程序.
活动2.分析下列程序,探究代数式求值的特点.
输入
????=?2
?
5????2?8????+2
?
5×(?2)2?8×(?2)+2
?
输出38
?
(1)按照上面程序,计算????=3,????=6时的输出值;
(2)任取????的两个值,按照上面的过程求值,并与同桌相互检查过程和结果是否正确.
?
23,134
?
定 义:像这样,用数值代替代数式中的字母,按照代数式中给出的运算计算出的结果,叫作代数式的值.这个过程叫作求代数式的值.
注意:1.代数式的值一般不是一个固定的值,它是随着代数式中字母取值的变化而变化的.
2.代数式里的字母可以用不同的数代入,但是这些数还须符合一定的要求 ,即所取的数值必须使代数式和它表示的实际数量有意义.例如,在上面 5 人及以下家庭一年的水费的例子中,b的值只能取不超过 80 的非负数.
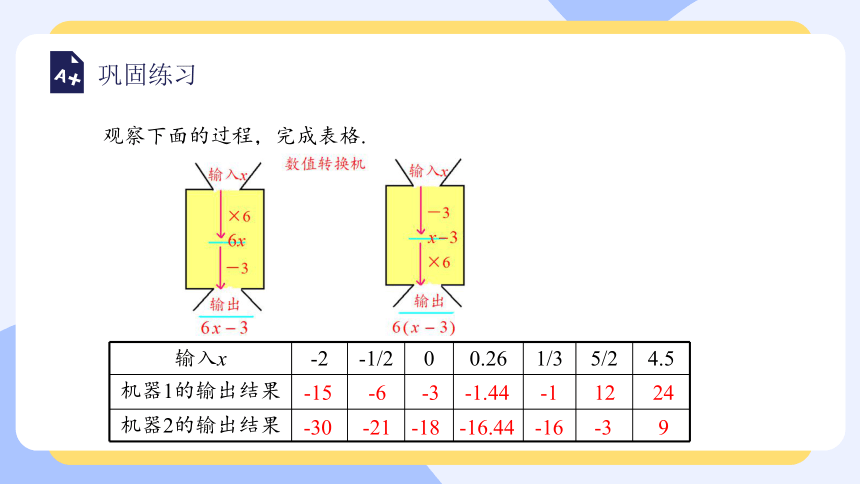
{5940675A-B579-460E-94D1-54222C63F5DA}输入x
-2
-1/2
0
0.26
1/3
5/2
4.5
机器1的输出结果
机器2的输出结果
-15
-6
-3
-1.44
-1
12
24
-30
-21
-18
-16.44
-16
-3
9
观察下面的过程,完成表格.
探究二.求代数式的值的步骤
活动1.阅读教材P119的例1,例2,思考下列问题.
思考:1.为什么代数式求值时要写“当”?
2.在代值求解时需要遵循哪些步骤以及有哪些注意事项?
1.代数式的值一般不是一个固定的值,它是随着代数式中字母取值的变化而变化的,因此在求解时“当”表示此刻特定条件的的求解
求代数式的值的一般步骤:
(1)代入:用给定的数代替代数式中相应的字母.
(2)计算:按照代数式中指明的运算,计算出代数式的值.
注意事项:
(1)代入时,除按已知给定的数值,将字母换成相应的数值外,其他的运算符号、运算顺序、原来的数值都不改变.
(2)代数式中省去的“×”或“·”,代入具体数后应恢复原来的“×”.若字母取值是分数或负数,则应根据实际情况适当添加括号.
1.求下列代数式的值时,代入过程正确的是( )
D
A.当 时
B.当 时
C.当 时
D.当 时
2.根据下列a,b的值,分别求代数式????2?????????的值:
?
解:(1)当 a =4,b =12 时,
????2??????????= 42?124?=13;
?
解:(2)当 ???? =?3,????=6 时,
????2?????????=(?3)2?6?3?=11.
?
(1)????=4, ????=12; (2)????=?3, ????=2.
?
活动2.观察代数式的结构求值.
1.这两个式子目标式?4x + 6y - 7和已知式 2x + 3y 有什么相似之处?小组讨论.
2.根据前面的发现,该如何去求目标式的值?
已知?2x + 3y = 5,则4x + 6y - 7的值是 ?.
4????=2×2????,6????=2×3????,目标式前半部分是已知式的?2 倍!
4????+6?????7=2(2????+3????)?7=2×5?7=3.
?
问题3:回顾整个过程,说说上式求解的关键是什么?
整体法核心:
1.寻找已知式与目标式的“公共结构”,如相同多项式、倍数关系(例如4x + 6y 是2x + 3y 的两倍);
2.将公共结构视为整体,通过代入、变形求解;
3.避免单独求解未知数,减少计算量.
1.填空.
(1) 若????+2????-1=0,则3????+6????的值是 ?.
(2)已知????2+2????=3,求2????2+4????+5的值是 ?.
?
3
?
11
?
如果把代数式里的字母用数代入,那么计算后得出的结果叫作这个代数式的一个值.
规范求解步骤
代数式的值
定义
代数式求值运算
整体法求值
1.当x=1时,代数式4-3x的值是( )
A.1 B.2 C.3 D.4
2.若 则x2-y3的值为( )
A.1 B.-1 C. D.2
3.如果2a+3b=5,那么4a+6b-7= .
已知a+b=5,ab=6 ,则ab-(a+b)=___.
A
C
3
1
4.填空:
输入a的值
输出结果
?2a+1
?
4
?4
?
0
?23
?
?7
?
9
1
73
?
5.完成下表:
a
-2
-1
0
1
2
3a+2
-3a+2
当a取的值越来越大时,代数式 3a+2的值随之有怎样的变化?代数式-3a+2的值随之有怎样的变化?
-4
-1
12
?
2
72
?
5
8
8
5
72
?
2
12
?
-1
-4
6.某公园的门票价格是:成人10元/张;学生5元/张.
(1)一个旅游团有成人x人、学生y人,那么该旅游团应付多少门票费?
(2)如果该旅游团有37个成人、15个学生,那么他们应付多少门票费?
解:(1)该旅游团应付的门票费是(10x+5y)元.
(2)把x=37,y=15代入代数式,得10x+5y =10×37+5×15 =445.
因此,他们应付445元门票费.
3.4 课时2 求实际问题中的代数式的值
第三章 代数式
1.在实际情境中,体会代数式的意义,能通过求代数式的值解决实际问题.
2.在解决实际问题的过程中,提高观察能力和归纳概括能力,联系实际生活.
小亮家离学校1280m.他每天步行上学,速度约是80m/min.我们用t (min)表示小亮从离开家开始的步行时间,那么如何表示小亮离开家的路程与距学校的路程呢?
情境1.小亮家离学校1280m.他每天步行上学,速度约是80m/min.我们用t (min)表示小亮从离开家开始的步行时间,S1(m)表示离开家的路程,S2 (m)表示距学校的路程.
(1)写出用t 分别表示S1和 S2 的代数式:S1= , S2 =____________;
(2)对具体的t值,计算S1和 S2的值,并填写下表:
80 t
1280-80 t
探究一.用代数式表示实际问题中的数量关系,并求解.
活动1.分析下列情境,讨论代数式与代数式的值在实际问题求解过程中的意义.
t/min
0
4
5.5
10
12.5
16
S1/m
S2/m
0
320
440
800
1000
1280
1280
960
840
480
280
0
(3)当t=7时,请你比较小亮离开家的路程与离学校的路程哪个远?
情境1.小亮家离学校1280m.他每天步行上学,速度约是80m/min.我们用t (min)表示小亮从离开家开始的步行时间,S1(m)表示离开家的路程,S2 (m)表示距学校的路程.
(3)当t=7时,请你比较小亮离开家的路程与离学校的路程哪个远?
活动1.分析下列情境,讨论代数式与代数式的值在实际问题求解过程中的意义.
解:t=7时, S1 =80t=80×7=560, S2 =1280-80t=1280-80×7=720.
因为560<720.
所以当t=7时,小亮距学校的路程远.
情境1.小亮家离学校1280m.他每天步行上学,速度约是80m/min.我们用t (min)表示小亮从离开家开始的步行时间,S1(m)表示离开家的路程,S2 (m)表示距学校的路程.
活动1.分析下列情境,讨论代数式与代数式的值在实际问题求解过程中的意义.
思考:
1.表格中的S1和S2在同时间对应的数量关系有什么特点?
2.通过这个表格,是否可以计算出任何一个时间中小亮的位置情况?
????1+????2=1280
?
可以
情境2.某农场购买了一台新型拖拉机用来耕地.为了测试耕地时的耗油量,用它试耕了三块地,其面积分别为0.4公顷,0.6公顷和1公顷.油量表的指针变化情况如图所示(油表中的一个大格表示10升油).
耕地面积/公顷
0.4
0.6
1
耗油量/升
(1)根据油量表指针的变化,估算耕地0.4公顷,0.6公顷,1公顷的耗油量(升),将结果填入表中.
10
15
25
耕地面积/公顷
0.4
0.6
1
耗油量/升
(2)设耕地a (公顷)耗油量为b(升),列代数式表示a和b之间的关系.
b=25a
10
15
25
(3)根据所列的关系式,求解下列问题:
①耕地面积为0.5公顷,2公顷时,耗油量分别是多少?
②如果两次耕地耗油量分别是12升和40升,那么所耕地的面积分别是多少公顷?
解:①当a=0.5时,b=0.5×25=12.5(升),当a=2时,b=2×25=50(升);
②由b=25a得a=????25,当b=12时,a=0.48公顷,当b=40时,a=1.6公顷.
?
情境2.某农场购买了一台新型拖拉机用来耕地.为了测试耕地时的耗油量,用它试耕了三块地,其面积分别为0.4公顷,0.6公顷和1公顷.油量表的指针变化情况如图所示(油表中的一个大格表示10升油).
思考:1.该情境的核心代数式是什么?
2.列出这个代数式的主要依据是什么?
3.根据所列出的代数式可以解决哪些相关问题?
b=25a
本题图所给出的数据
如耕多少地耗油多少,根据耗油的数量判断耕地的数量等
列代数式解决实际问题:
1.通过生活中的数量关系(文字、图表、图象等)可以列出代数式,进而解决生活中的数量关系问题.
2.代数式里的字母可取不同的值,但是所取的数值不能使代数式或它表示的实际问题失去意义.
1.树的高度与树生长的年数有关,测得某棵树的数据如下:(树苗原高100厘米)
(1)用含有字母n的代数式表示生长了n年的树苗的高度an;
(2)生长了11年的树的高度是多少?
解:(1)an=100+5n ;
(2)an=100+5n=100+5×11=155(厘米).
2.某企业去年的年产值为a亿元,今年比去年增长了10%.如果明年还能按这个速度增长,请你预测一下,该企业明年的年产值能达到多少亿元?如果去年的年产值是2亿元,那么预计明年的年产值是多少亿元?
解:由题意可得,今年的年产值为 ????(1+10%)亿元,
所以明年的年产值为 ????(1+10%)(1+10%)=1.21????(亿元).
若去年的年产值为2亿元,则明年的年产值1.21????=1.21×2=2.42(亿元)
答:该企业明年的年产值将能达到1.21a亿元.由去年的年产值是2亿元,可以
预测明年的年产值是2.42亿元.
第三章 代数式
3.4 课时1 求代数式的值
第三章 代数式
1.理解代数式的值的概念,会求代数式的值,提高运算能力.
2.通过求代数式的值,体会代数式实际上是由计算程序
反映的一种数量关系.
如图所示,由三种图示方法得到空心方阵的总点数分别为4n-4,4(n-l),2n +2(n- 2).当字母n是一个具体数值的时候,还能算出这个空心方阵总点数吗?
...
...
...
...
n个点
n个点
4n-4
探究一.代数式的值的概念
活动1.分析下列问题,同桌讨论代数式的值的概念.
(1)当n取4, 10, 15,25等值时,分别代入上面的代数式,计算出代数式的值,并思考,对于n的同一个值,同学们得到的结果都一样吗?
(2)根据(1)中n的取值,如何计算出4n-4的值呢?
当????=4时,4????-4=4×4?4=12;
当????=10时,4????-4=4×10?4=36;
当????=15时,4????-4=4×15?4=56;
当????=4时,4????-4=4×25?4=96;
?
对代数式中的字母代入不同的值,都可以求出代数式相应的值.一个代数式,可以看做一个计算程序.
活动2.分析下列程序,探究代数式求值的特点.
输入
????=?2
?
5????2?8????+2
?
5×(?2)2?8×(?2)+2
?
输出38
?
(1)按照上面程序,计算????=3,????=6时的输出值;
(2)任取????的两个值,按照上面的过程求值,并与同桌相互检查过程和结果是否正确.
?
23,134
?
定 义:像这样,用数值代替代数式中的字母,按照代数式中给出的运算计算出的结果,叫作代数式的值.这个过程叫作求代数式的值.
注意:1.代数式的值一般不是一个固定的值,它是随着代数式中字母取值的变化而变化的.
2.代数式里的字母可以用不同的数代入,但是这些数还须符合一定的要求 ,即所取的数值必须使代数式和它表示的实际数量有意义.例如,在上面 5 人及以下家庭一年的水费的例子中,b的值只能取不超过 80 的非负数.
{5940675A-B579-460E-94D1-54222C63F5DA}输入x
-2
-1/2
0
0.26
1/3
5/2
4.5
机器1的输出结果
机器2的输出结果
-15
-6
-3
-1.44
-1
12
24
-30
-21
-18
-16.44
-16
-3
9
观察下面的过程,完成表格.
探究二.求代数式的值的步骤
活动1.阅读教材P119的例1,例2,思考下列问题.
思考:1.为什么代数式求值时要写“当”?
2.在代值求解时需要遵循哪些步骤以及有哪些注意事项?
1.代数式的值一般不是一个固定的值,它是随着代数式中字母取值的变化而变化的,因此在求解时“当”表示此刻特定条件的的求解
求代数式的值的一般步骤:
(1)代入:用给定的数代替代数式中相应的字母.
(2)计算:按照代数式中指明的运算,计算出代数式的值.
注意事项:
(1)代入时,除按已知给定的数值,将字母换成相应的数值外,其他的运算符号、运算顺序、原来的数值都不改变.
(2)代数式中省去的“×”或“·”,代入具体数后应恢复原来的“×”.若字母取值是分数或负数,则应根据实际情况适当添加括号.
1.求下列代数式的值时,代入过程正确的是( )
D
A.当 时
B.当 时
C.当 时
D.当 时
2.根据下列a,b的值,分别求代数式????2?????????的值:
?
解:(1)当 a =4,b =12 时,
????2??????????= 42?124?=13;
?
解:(2)当 ???? =?3,????=6 时,
????2?????????=(?3)2?6?3?=11.
?
(1)????=4, ????=12; (2)????=?3, ????=2.
?
活动2.观察代数式的结构求值.
1.这两个式子目标式?4x + 6y - 7和已知式 2x + 3y 有什么相似之处?小组讨论.
2.根据前面的发现,该如何去求目标式的值?
已知?2x + 3y = 5,则4x + 6y - 7的值是 ?.
4????=2×2????,6????=2×3????,目标式前半部分是已知式的?2 倍!
4????+6?????7=2(2????+3????)?7=2×5?7=3.
?
问题3:回顾整个过程,说说上式求解的关键是什么?
整体法核心:
1.寻找已知式与目标式的“公共结构”,如相同多项式、倍数关系(例如4x + 6y 是2x + 3y 的两倍);
2.将公共结构视为整体,通过代入、变形求解;
3.避免单独求解未知数,减少计算量.
1.填空.
(1) 若????+2????-1=0,则3????+6????的值是 ?.
(2)已知????2+2????=3,求2????2+4????+5的值是 ?.
?
3
?
11
?
如果把代数式里的字母用数代入,那么计算后得出的结果叫作这个代数式的一个值.
规范求解步骤
代数式的值
定义
代数式求值运算
整体法求值
1.当x=1时,代数式4-3x的值是( )
A.1 B.2 C.3 D.4
2.若 则x2-y3的值为( )
A.1 B.-1 C. D.2
3.如果2a+3b=5,那么4a+6b-7= .
已知a+b=5,ab=6 ,则ab-(a+b)=___.
A
C
3
1
4.填空:
输入a的值
输出结果
?2a+1
?
4
?4
?
0
?23
?
?7
?
9
1
73
?
5.完成下表:
a
-2
-1
0
1
2
3a+2
-3a+2
当a取的值越来越大时,代数式 3a+2的值随之有怎样的变化?代数式-3a+2的值随之有怎样的变化?
-4
-1
12
?
2
72
?
5
8
8
5
72
?
2
12
?
-1
-4
6.某公园的门票价格是:成人10元/张;学生5元/张.
(1)一个旅游团有成人x人、学生y人,那么该旅游团应付多少门票费?
(2)如果该旅游团有37个成人、15个学生,那么他们应付多少门票费?
解:(1)该旅游团应付的门票费是(10x+5y)元.
(2)把x=37,y=15代入代数式,得10x+5y =10×37+5×15 =445.
因此,他们应付445元门票费.
3.4 课时2 求实际问题中的代数式的值
第三章 代数式
1.在实际情境中,体会代数式的意义,能通过求代数式的值解决实际问题.
2.在解决实际问题的过程中,提高观察能力和归纳概括能力,联系实际生活.
小亮家离学校1280m.他每天步行上学,速度约是80m/min.我们用t (min)表示小亮从离开家开始的步行时间,那么如何表示小亮离开家的路程与距学校的路程呢?
情境1.小亮家离学校1280m.他每天步行上学,速度约是80m/min.我们用t (min)表示小亮从离开家开始的步行时间,S1(m)表示离开家的路程,S2 (m)表示距学校的路程.
(1)写出用t 分别表示S1和 S2 的代数式:S1= , S2 =____________;
(2)对具体的t值,计算S1和 S2的值,并填写下表:
80 t
1280-80 t
探究一.用代数式表示实际问题中的数量关系,并求解.
活动1.分析下列情境,讨论代数式与代数式的值在实际问题求解过程中的意义.
t/min
0
4
5.5
10
12.5
16
S1/m
S2/m
0
320
440
800
1000
1280
1280
960
840
480
280
0
(3)当t=7时,请你比较小亮离开家的路程与离学校的路程哪个远?
情境1.小亮家离学校1280m.他每天步行上学,速度约是80m/min.我们用t (min)表示小亮从离开家开始的步行时间,S1(m)表示离开家的路程,S2 (m)表示距学校的路程.
(3)当t=7时,请你比较小亮离开家的路程与离学校的路程哪个远?
活动1.分析下列情境,讨论代数式与代数式的值在实际问题求解过程中的意义.
解:t=7时, S1 =80t=80×7=560, S2 =1280-80t=1280-80×7=720.
因为560<720.
所以当t=7时,小亮距学校的路程远.
情境1.小亮家离学校1280m.他每天步行上学,速度约是80m/min.我们用t (min)表示小亮从离开家开始的步行时间,S1(m)表示离开家的路程,S2 (m)表示距学校的路程.
活动1.分析下列情境,讨论代数式与代数式的值在实际问题求解过程中的意义.
思考:
1.表格中的S1和S2在同时间对应的数量关系有什么特点?
2.通过这个表格,是否可以计算出任何一个时间中小亮的位置情况?
????1+????2=1280
?
可以
情境2.某农场购买了一台新型拖拉机用来耕地.为了测试耕地时的耗油量,用它试耕了三块地,其面积分别为0.4公顷,0.6公顷和1公顷.油量表的指针变化情况如图所示(油表中的一个大格表示10升油).
耕地面积/公顷
0.4
0.6
1
耗油量/升
(1)根据油量表指针的变化,估算耕地0.4公顷,0.6公顷,1公顷的耗油量(升),将结果填入表中.
10
15
25
耕地面积/公顷
0.4
0.6
1
耗油量/升
(2)设耕地a (公顷)耗油量为b(升),列代数式表示a和b之间的关系.
b=25a
10
15
25
(3)根据所列的关系式,求解下列问题:
①耕地面积为0.5公顷,2公顷时,耗油量分别是多少?
②如果两次耕地耗油量分别是12升和40升,那么所耕地的面积分别是多少公顷?
解:①当a=0.5时,b=0.5×25=12.5(升),当a=2时,b=2×25=50(升);
②由b=25a得a=????25,当b=12时,a=0.48公顷,当b=40时,a=1.6公顷.
?
情境2.某农场购买了一台新型拖拉机用来耕地.为了测试耕地时的耗油量,用它试耕了三块地,其面积分别为0.4公顷,0.6公顷和1公顷.油量表的指针变化情况如图所示(油表中的一个大格表示10升油).
思考:1.该情境的核心代数式是什么?
2.列出这个代数式的主要依据是什么?
3.根据所列出的代数式可以解决哪些相关问题?
b=25a
本题图所给出的数据
如耕多少地耗油多少,根据耗油的数量判断耕地的数量等
列代数式解决实际问题:
1.通过生活中的数量关系(文字、图表、图象等)可以列出代数式,进而解决生活中的数量关系问题.
2.代数式里的字母可取不同的值,但是所取的数值不能使代数式或它表示的实际问题失去意义.
1.树的高度与树生长的年数有关,测得某棵树的数据如下:(树苗原高100厘米)
(1)用含有字母n的代数式表示生长了n年的树苗的高度an;
(2)生长了11年的树的高度是多少?
解:(1)an=100+5n ;
(2)an=100+5n=100+5×11=155(厘米).
2.某企业去年的年产值为a亿元,今年比去年增长了10%.如果明年还能按这个速度增长,请你预测一下,该企业明年的年产值能达到多少亿元?如果去年的年产值是2亿元,那么预计明年的年产值是多少亿元?
解:由题意可得,今年的年产值为 ????(1+10%)亿元,
所以明年的年产值为 ????(1+10%)(1+10%)=1.21????(亿元).
若去年的年产值为2亿元,则明年的年产值1.21????=1.21×2=2.42(亿元)
答:该企业明年的年产值将能达到1.21a亿元.由去年的年产值是2亿元,可以
预测明年的年产值是2.42亿元.
同课章节目录
- 第一章 有理数
- 1.1 正数和负数
- 1.2 数轴
- 1.3 绝对值与相反数
- 1.4 有理数的大小
- 1.5 有理数的加法
- 1.6 有理数的减法
- 1.7 有理数的加减混合运算
- 1.8 有理数的乘法
- 1.9 有理数的除法
- 1.10 有理数的乘方
- 1.11 有理数的混合运算
- 1.12 计算器的使用
- 第二章 几何图形的初步认识
- 2.1 从生活中认识几何图形
- 2.2 点和线
- 2.3 线段长短的比较
- 2.4 线段的和与差
- 2.5 角以及角的度量
- 2.6 角的大小
- 2.7 角的和与差
- 2.8 平面图形的旋转
- 第三章 代数式
- 3.1 用字母表示数
- 3.2 代数式
- 3.3 代数式的值
- 第四章 整式的加减
- 4.1 整式
- 4.2 合并同类项
- 4.3 去括号
- 4.4 整式的加减
- 第五章 一元一次方程
- 5.1一元一次方程
- 5.2 等式的基本性质
- 5.3 解一元一次方程
- 5.4 一元一次方程的应用
