全册复习质量评估(含答案)2025-2026学年数学人教版(2024)七年级上册
文档属性
| 名称 | 全册复习质量评估(含答案)2025-2026学年数学人教版(2024)七年级上册 |  | |
| 格式 | docx | ||
| 文件大小 | 141.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-24 00:22:04 | ||
图片预览



文档简介
全册复习 质量评估
[时间:120分钟 分值:120分]
一、选择题(本大题共10个小题,每小题3分,共30分)
1.的绝对值是( )
A.5 B. C. D.
2.我国的北斗卫星导航系统星座部署完成,其中一颗中高轨道卫星高度大约是.数据12 500 000用科学记数法表示为( )
A. B. C. D.
3.下列去括号正确的是( )
A.
B.
C.
D.
4.已知与是同类项,则的值为( )
A.3 B.2 C.1 D.0
5.“学而不思则罔,思而不学则殆”体现了学习和思考的重要性.如图是每个面上都有一个汉字的正方体的一种表面展开图,那么在原正方体中与“学”字相对面上的字是( )
A.不 B.思 C.则 D.罔
6.已知的值为4,则代数式的值为( )
A. B.4 C.12 D.20
7.幻方历史悠久,传说最早出现在夏禹时代的“洛书”.洛书用今天的数学符号翻译出来,就是一个三阶幻方(如图①),将9个数填在的方格中,如果满足每行、每列、每条对角线上的三个数之和都相等,就得到一个广义的三阶幻方.图②的方格中填写了一些数和字母,若能构成一个广义的三阶幻方,则的值为( )
A.18 B.10 C.8 D.2
8.已知,,在数轴上的对应点的位置如图所示,则( )
A. B.
C. D.
9.下列说法中,正确的有( )
①直线和直线是同一条直线;
②若,则为线段的中点;
③同角的补角相等;
④表示的平方与的差的3倍;
⑤绝对值等于它本身的数是正数;
⑥20.196精确到百分位得20.2.
A.2个 B.3个 C.4个 D.5个
10.某款服装进价120元/件,标价元/件,商店对这款服装推出“买两件,第一件原价,第二件打六折”的促销活动,按这种促销方式销售两件该款服装,商店仍获利48元,则的值为( )
A.185 B.190 C.180 D.195
二、填空题(本大题共6个小题,每小题3分,共18分)
11.若单项式的系数为,次数为,则_ _ _ _ _ _ .
12.计算:_ _ _ _ _ _ _ _ _ _ .
13.已知一个角的补角比这个角的余角的3倍少 ,则这个角的度数为_ _ _ _ _ _ .
14.若是最大的负整数,是绝对值最小的数,与互为相反数,与互为倒数,则_ _ _ _ _ _ .
15.一套仪器由一个A部件和三个B部件构成,用钢材可做30个A部件或150个B部件.现要用钢材制作这种仪器,设应用钢材做A部件,剩余钢材做B部件,恰好配套,则可列方程为_ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ .
16.蜜蜂是自然界神奇的“建筑师”,它能用最少的材料造成最牢固的建筑物“蜂窝”.观察下列的蜂窝图,若将每一个六边形“”看成1个建筑单位,则第1个图中共有4个建筑单位,第2个图中共有7个建筑单位,第3个图中共有10个建筑单位 以类推,则第2 025个图中共有_ _ _ _ 个建筑单位.
三、解答题(本大题共9个小题,共72分)
17.(6分)计算:.
18.(6分)解方程:.
19.(6分)先化简,再求值:,其中,.
20.(8分)已知,将关于的方程记作方程.
(1) 当,时,直接写出方程的解为_ _ _ _ _ _ ;
(2) 若方程的解为,求多项式的值;
(3) 若方程的解为,求关于的方程的解.
21.(8分)站和站相距,一列慢车从站开出,速度为,一列快车从站开出,速度为.
(1) 若两车相向而行,同时出发,行驶几小时后两车相遇?
(2) 若两车同向而行,慢车在前,慢车开出后快车再出发,快车开出几小时后追上慢车?
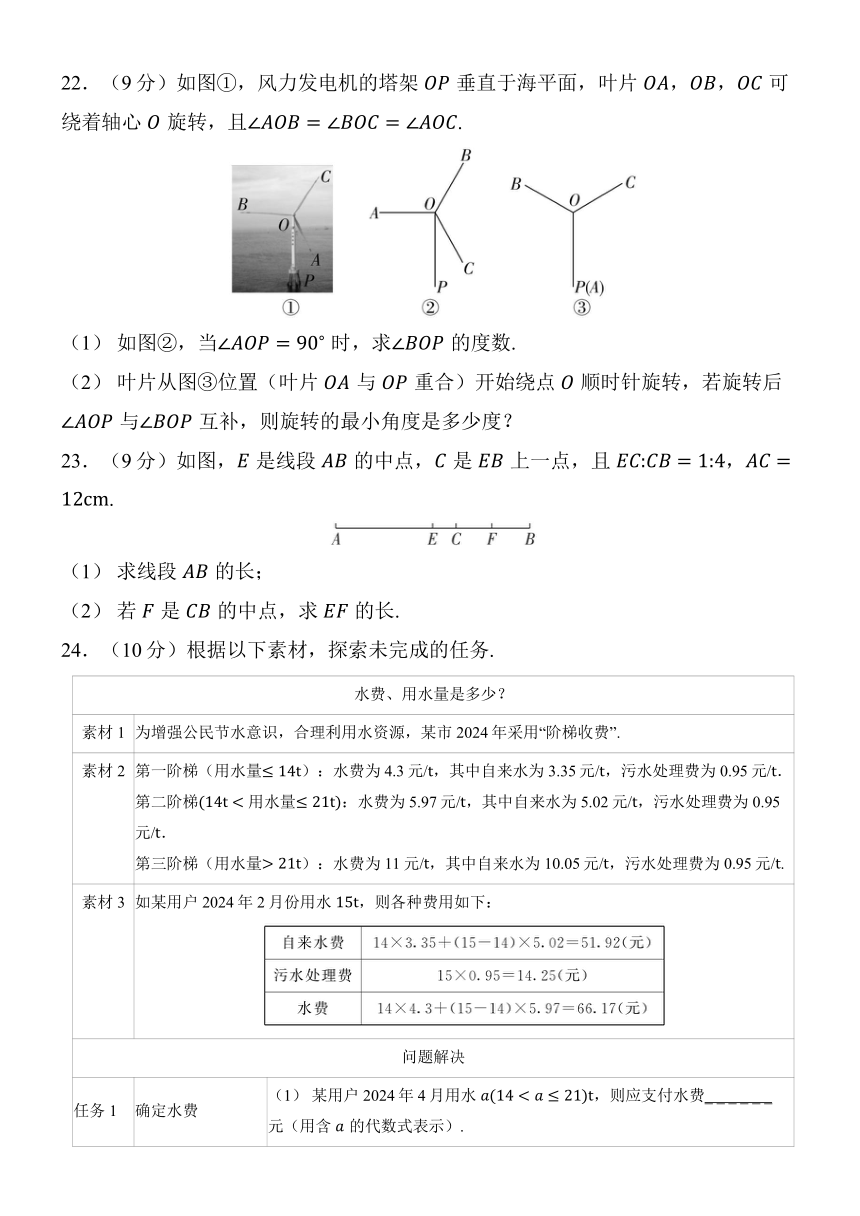
22.(9分)如图①,风力发电机的塔架垂直于海平面,叶片,,可绕着轴心旋转,且.
(1) 如图②,当 时,求的度数.
(2) 叶片从图③位置(叶片与重合)开始绕点顺时针旋转,若旋转后与互补,则旋转的最小角度是多少度?
23.(9分)如图,是线段的中点,是上一点,且,.
(1) 求线段的长;
(2) 若是的中点,求的长.
24.(10分)根据以下素材,探索未完成的任务.
水费、用水量是多少?
素材1 为增强公民节水意识,合理利用水资源,某市2024年采用“阶梯收费”.
素材2 第一阶梯(用水量):水费为4.3元/,其中自来水为3.35元/,污水处理费为0.95元/. 第二阶梯 用水量:水费为5.97元/,其中自来水为5.02元/,污水处理费为0.95元/. 第三阶梯(用水量):水费为11元/,其中自来水为10.05元/,污水处理费为0.95元/.
素材3 如某用户2024年2月份用水,则各种费用如下:
问题解决
任务1 确定水费 (1) 某用户2024年4月用水,则应支付水费_ _ _ _ _ _ 元(用含的代数式表示).
任务2 确定污水处理费 (2) 已知某用户2024年5月份所支付水费中,自来水费为66.98元,则该用户5月份需支付污水处理费多少元?
任务3 确定用水量 (3) 如果该用户2024年6、7月份共用水月份用水量超过6月份用水量),共支付水费209.01元,则该用户6、7月份各用水多少吨?
25.(10分)如图①,已知射线是内部的一条射线,若射线与射线的夹角,则我们称射线是射线的“友好线”.例如,如图②, , ,则,称射线是射线的“友好线”;同时,由于,称射线是射线的“友好线”.
(1) 如图③, ,射线是射线的“友好线”,则_ _ _ _ .
(2) 如图④, ,射线从与射线重合的位置开始,绕点以的速度逆时针旋转;同时射线从与射线重合的位置开始,绕点以的速度顺时针旋转.设运动时间为.
① 当射线与射线重合时,运动停止.问是否存在某个时刻,使得的度数是 ?若存在,求出的值;若不存在,请说明理由.
② 在射线与射线重合前,是否存在射线,,中有一条射线是另一条射线的“友好线”?若存在,请求出的值;若不存在,请说明理由.
一、选择题(本大题共10个小题,每小题3分,共30分)
1.A 2.B 3.A 4.C 5.C 6.D 7.A 8.A 9.B 10.C
二、填空题(本大题共6个小题,每小题3分,共18分)
11.
12.
13.
14.
15.
16.6 076
三、解答题(本大题共9个小题,共72分)
17.解:原式
.
18.解:去分母,得.
去括号,得.
移项,得.
合并同类项,得.
系数化为1,得.
19.解:原式.
当,时,
原式.
20.(1)
(2) 解:将代入方程,得,
,
.
(3) 由题意,得,
,.
关于的方程可变为,
,
解得.
21.(1) 解:设行驶后两车相遇.
由题意,得,
解得.
答:行驶后两车相遇.
(2) 设快车开出后追上慢车,则此时慢车开出.
由题意,得.
解得.
答:快车开出后追上慢车.
22.(1) 解:, ,
.
,
,
.
(2) 设旋转的最小角度是 ,
, .
与互补,
,
即,
解得,
旋转的最小角度是 .
23.(1) 解:设的长为,
,,
,.
又是线段的中点,
,,.
又,,
,解得,
.
(2) 是线段的中点,.
又,.
24.(1)
(2) 解:(元),(元),
而,
月份用水量超过不超过.
设该用户5月份的用水量为,
由题意,得,
解得,
故(元).
答:该用户5月份需支付污水处理费为17.1元.
(3) 设该用户6月份的用水量为,则7月份的用水量为,
月份用水量超过6月份用水量,,.
当时,
,
解得(不合题意,舍去);
当时,,
解得,
.
答:该户居民6、7月份各用水和.
25.(1) 40
(2) ① 解:当射线与射重合时,用时,
由题意,得 , .
(2) ① 存在. ,
,
即 ,
解得.
② 存在.当射线是射线的“友好线”时,,
即,
解得;
当射线是射线的“友好线”时,,
即,
解得.
综上所述,存在,的值为20或30.
[时间:120分钟 分值:120分]
一、选择题(本大题共10个小题,每小题3分,共30分)
1.的绝对值是( )
A.5 B. C. D.
2.我国的北斗卫星导航系统星座部署完成,其中一颗中高轨道卫星高度大约是.数据12 500 000用科学记数法表示为( )
A. B. C. D.
3.下列去括号正确的是( )
A.
B.
C.
D.
4.已知与是同类项,则的值为( )
A.3 B.2 C.1 D.0
5.“学而不思则罔,思而不学则殆”体现了学习和思考的重要性.如图是每个面上都有一个汉字的正方体的一种表面展开图,那么在原正方体中与“学”字相对面上的字是( )
A.不 B.思 C.则 D.罔
6.已知的值为4,则代数式的值为( )
A. B.4 C.12 D.20
7.幻方历史悠久,传说最早出现在夏禹时代的“洛书”.洛书用今天的数学符号翻译出来,就是一个三阶幻方(如图①),将9个数填在的方格中,如果满足每行、每列、每条对角线上的三个数之和都相等,就得到一个广义的三阶幻方.图②的方格中填写了一些数和字母,若能构成一个广义的三阶幻方,则的值为( )
A.18 B.10 C.8 D.2
8.已知,,在数轴上的对应点的位置如图所示,则( )
A. B.
C. D.
9.下列说法中,正确的有( )
①直线和直线是同一条直线;
②若,则为线段的中点;
③同角的补角相等;
④表示的平方与的差的3倍;
⑤绝对值等于它本身的数是正数;
⑥20.196精确到百分位得20.2.
A.2个 B.3个 C.4个 D.5个
10.某款服装进价120元/件,标价元/件,商店对这款服装推出“买两件,第一件原价,第二件打六折”的促销活动,按这种促销方式销售两件该款服装,商店仍获利48元,则的值为( )
A.185 B.190 C.180 D.195
二、填空题(本大题共6个小题,每小题3分,共18分)
11.若单项式的系数为,次数为,则_ _ _ _ _ _ .
12.计算:_ _ _ _ _ _ _ _ _ _ .
13.已知一个角的补角比这个角的余角的3倍少 ,则这个角的度数为_ _ _ _ _ _ .
14.若是最大的负整数,是绝对值最小的数,与互为相反数,与互为倒数,则_ _ _ _ _ _ .
15.一套仪器由一个A部件和三个B部件构成,用钢材可做30个A部件或150个B部件.现要用钢材制作这种仪器,设应用钢材做A部件,剩余钢材做B部件,恰好配套,则可列方程为_ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ .
16.蜜蜂是自然界神奇的“建筑师”,它能用最少的材料造成最牢固的建筑物“蜂窝”.观察下列的蜂窝图,若将每一个六边形“”看成1个建筑单位,则第1个图中共有4个建筑单位,第2个图中共有7个建筑单位,第3个图中共有10个建筑单位 以类推,则第2 025个图中共有_ _ _ _ 个建筑单位.
三、解答题(本大题共9个小题,共72分)
17.(6分)计算:.
18.(6分)解方程:.
19.(6分)先化简,再求值:,其中,.
20.(8分)已知,将关于的方程记作方程.
(1) 当,时,直接写出方程的解为_ _ _ _ _ _ ;
(2) 若方程的解为,求多项式的值;
(3) 若方程的解为,求关于的方程的解.
21.(8分)站和站相距,一列慢车从站开出,速度为,一列快车从站开出,速度为.
(1) 若两车相向而行,同时出发,行驶几小时后两车相遇?
(2) 若两车同向而行,慢车在前,慢车开出后快车再出发,快车开出几小时后追上慢车?
22.(9分)如图①,风力发电机的塔架垂直于海平面,叶片,,可绕着轴心旋转,且.
(1) 如图②,当 时,求的度数.
(2) 叶片从图③位置(叶片与重合)开始绕点顺时针旋转,若旋转后与互补,则旋转的最小角度是多少度?
23.(9分)如图,是线段的中点,是上一点,且,.
(1) 求线段的长;
(2) 若是的中点,求的长.
24.(10分)根据以下素材,探索未完成的任务.
水费、用水量是多少?
素材1 为增强公民节水意识,合理利用水资源,某市2024年采用“阶梯收费”.
素材2 第一阶梯(用水量):水费为4.3元/,其中自来水为3.35元/,污水处理费为0.95元/. 第二阶梯 用水量:水费为5.97元/,其中自来水为5.02元/,污水处理费为0.95元/. 第三阶梯(用水量):水费为11元/,其中自来水为10.05元/,污水处理费为0.95元/.
素材3 如某用户2024年2月份用水,则各种费用如下:
问题解决
任务1 确定水费 (1) 某用户2024年4月用水,则应支付水费_ _ _ _ _ _ 元(用含的代数式表示).
任务2 确定污水处理费 (2) 已知某用户2024年5月份所支付水费中,自来水费为66.98元,则该用户5月份需支付污水处理费多少元?
任务3 确定用水量 (3) 如果该用户2024年6、7月份共用水月份用水量超过6月份用水量),共支付水费209.01元,则该用户6、7月份各用水多少吨?
25.(10分)如图①,已知射线是内部的一条射线,若射线与射线的夹角,则我们称射线是射线的“友好线”.例如,如图②, , ,则,称射线是射线的“友好线”;同时,由于,称射线是射线的“友好线”.
(1) 如图③, ,射线是射线的“友好线”,则_ _ _ _ .
(2) 如图④, ,射线从与射线重合的位置开始,绕点以的速度逆时针旋转;同时射线从与射线重合的位置开始,绕点以的速度顺时针旋转.设运动时间为.
① 当射线与射线重合时,运动停止.问是否存在某个时刻,使得的度数是 ?若存在,求出的值;若不存在,请说明理由.
② 在射线与射线重合前,是否存在射线,,中有一条射线是另一条射线的“友好线”?若存在,请求出的值;若不存在,请说明理由.
一、选择题(本大题共10个小题,每小题3分,共30分)
1.A 2.B 3.A 4.C 5.C 6.D 7.A 8.A 9.B 10.C
二、填空题(本大题共6个小题,每小题3分,共18分)
11.
12.
13.
14.
15.
16.6 076
三、解答题(本大题共9个小题,共72分)
17.解:原式
.
18.解:去分母,得.
去括号,得.
移项,得.
合并同类项,得.
系数化为1,得.
19.解:原式.
当,时,
原式.
20.(1)
(2) 解:将代入方程,得,
,
.
(3) 由题意,得,
,.
关于的方程可变为,
,
解得.
21.(1) 解:设行驶后两车相遇.
由题意,得,
解得.
答:行驶后两车相遇.
(2) 设快车开出后追上慢车,则此时慢车开出.
由题意,得.
解得.
答:快车开出后追上慢车.
22.(1) 解:, ,
.
,
,
.
(2) 设旋转的最小角度是 ,
, .
与互补,
,
即,
解得,
旋转的最小角度是 .
23.(1) 解:设的长为,
,,
,.
又是线段的中点,
,,.
又,,
,解得,
.
(2) 是线段的中点,.
又,.
24.(1)
(2) 解:(元),(元),
而,
月份用水量超过不超过.
设该用户5月份的用水量为,
由题意,得,
解得,
故(元).
答:该用户5月份需支付污水处理费为17.1元.
(3) 设该用户6月份的用水量为,则7月份的用水量为,
月份用水量超过6月份用水量,,.
当时,
,
解得(不合题意,舍去);
当时,,
解得,
.
答:该户居民6、7月份各用水和.
25.(1) 40
(2) ① 解:当射线与射重合时,用时,
由题意,得 , .
(2) ① 存在. ,
,
即 ,
解得.
② 存在.当射线是射线的“友好线”时,,
即,
解得;
当射线是射线的“友好线”时,,
即,
解得.
综上所述,存在,的值为20或30.
同课章节目录
