2025年浙江省杭州市余杭区信达外国语学校中考数学三模试卷(含部分答案)
文档属性
| 名称 | 2025年浙江省杭州市余杭区信达外国语学校中考数学三模试卷(含部分答案) |  | |
| 格式 | docx | ||
| 文件大小 | 148.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-24 10:31:04 | ||
图片预览



文档简介
2025年浙江省杭州市余杭区信达外国语学校中考数学三模试卷
一、选择题:本题共10小题,每小题3分,共30分。在每小题给出的选项中,只有一项是符合题目要求的。
1.下列实数中,无理数是( )
A. -2 B. 0 C. D.
2.下列几何体由5个相同的小正方体搭成,其左视图是( )
A.
B.
C.
D.
3.某校30个班级在学校“书香班级”的创建活动中,以班级为单位进行捐书,根据班级的捐书量制作下表:
数量/册 160 175 183 190 198 203 212 225
班级数 2 4 7 5 6 3 2 1
这组数据的众数和中位数分别是( )
A. 7,5.5 B. 7,5 C. 183,190 D. 183,194
4.如图,将一个正方形纸片沿图中虚线剪开,能拼成下列四个图形,其中是中心对称图形的是( )
A.
B.
C.
D.
5.下列运算正确的是( )
A. (-a3)2=-a6 B. a2 a3=a6 C. (a+b)2=a2+b2 D. 3a2-2a2=a2
6.某商场在五一期间推出促销活动,活动期间内,凡是购物即可参与抽奖.不透明的盒子里装有12张质地、大小完全相同的纸片,其中2张纸片写有奖品为“扫地机器人一台”,4张纸片写有奖品为“餐具一套”,6张纸片写有奖品为“纸巾一袋”.从盒中任意摸出1张纸片,摸出奖品为“扫地机器人一台”的概率是( )
A. B. C. D.
7.A,B,C,D四点在⊙O上的位置如图所示,∠OAB=10°,∠ABD=20°,则∠C的度数为( )
A. 130°
B. 120°
C. 110°
D. 100°
8.晚托期间,八(1)班学生积极参与文体活动.起初,篮球组的报名人数比羽毛球组报名人数的还多4人;后来,羽毛球组有8人改报了篮球组,此时,篮球组的报名人数是羽毛球组报名人数的2倍.设起初报名篮球组的人数为x,报名羽毛球组的人数为y,则下面所列方程组正确的是( )
A. B.
C. D.
9.二次函数y=(x+1)2+(x+2)2与y=(x+a)2+(x+b)2的图象关于y轴对称,则(a-1)2+(b-1)2的值为( )
A. 0 B. 1 C. 10 D. 13
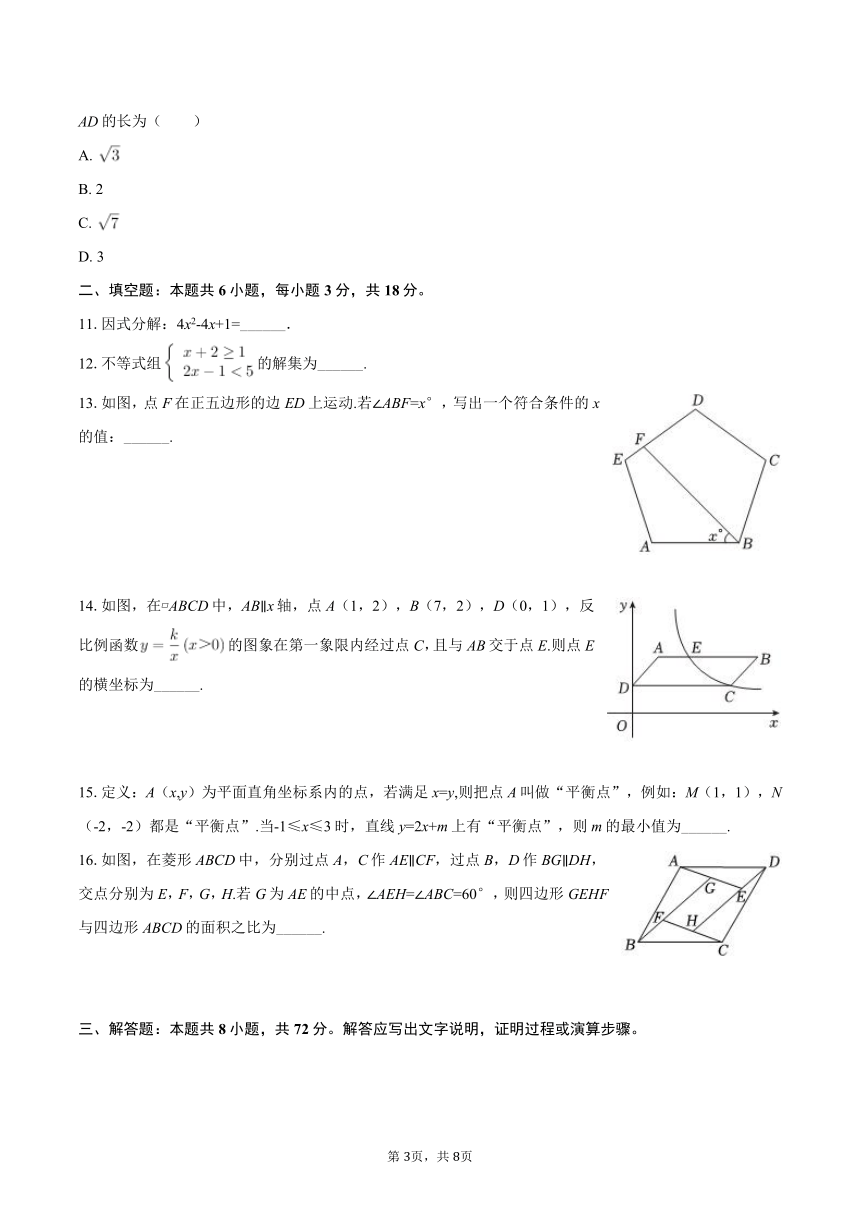
10.在等边△ABC中,D为△ABC内的一点,∠BDC=120°,∠ADB=90°,CD=1,则AD的长为( )
A.
B. 2
C.
D. 3
二、填空题:本题共6小题,每小题3分,共18分。
11.因式分解:4x2-4x+1=______.
12.不等式组的解集为______.
13.如图,点F在正五边形的边ED上运动.若∠ABF=x°,写出一个符合条件的x的值:______.
14.如图,在 ABCD中,AB∥x轴,点A(1,2),B(7,2),D(0,1),反比例函数的图象在第一象限内经过点C,且与AB交于点E.则点E的横坐标为______.
15.定义:A(x,y)为平面直角坐标系内的点,若满足x=y,则把点A叫做“平衡点”,例如:M(1,1),N(-2,-2)都是“平衡点”.当-1≤x≤3时,直线y=2x+m上有“平衡点”,则m的最小值为______.
16.如图,在菱形ABCD中,分别过点A,C作AE∥CF,过点B,D作BG∥DH,交点分别为E,F,G,H.若G为AE的中点,∠AEH=∠ABC=60°,则四边形GEHF与四边形ABCD的面积之比为______.
三、解答题:本题共8小题,共72分。解答应写出文字说明,证明过程或演算步骤。
17.(本小题8分)
计算:.
18.(本小题8分)
解分式方程:.
19.(本小题8分)
司南是我国古代辨别方向用的一种仪器.其早在战国时期就已被发明,是现在所用指南针的始祖.如图1,司南中心为一圆形,圆心为点O,直径为20.根据八个方位将圆形八等分(图2中点A-H),过点E作⊙O的切线,与AG的延长线交于点M,连接EG.
(1)求∠AEG的值.
(2)求线段MG的长.
20.(本小题8分)
某校举办“十佳歌手”演唱比赛,五位评委进行现场打分,将甲、乙、丙三位选手的得分数据整理成下列统计图.根据以上信息,解答下列问题.
(1)完成表格:
平均数/分 中位数/分 众数/分 方差
甲 8.8 ①______ 8和9 0.56
乙 ②______ 9 9 0.96
丙 8.8 8 ③______ 0.96
(2)从三位选手中选一位参加市级比赛,你认为选谁更合适?请说明理由.
21.(本小题8分)
如图1,AC=2AB=4.以点A为圆心,适当长为半径画弧,分别交AB,AC于点M,N.分别以点M,N为圆心,以大于的长为半径画弧,两弧在∠BAC内交于点E.作射线AE.过点C作CD∥AB,交AE于点D.
(1)求CD的长;
(2)如图2,连接BD.分别以点A,C为圆心,大于的长为半径画弧,两弧交于点P,Q.作直线PQ,交AB的延长线于点F.连接CF,交BD于点G.当∠BAC=60°时,求的值.
22.(本小题10分)
目前,无人机航拍越来越多的应用于各种领域.现对甲、乙两台无人机同时开始操作,甲无人机先匀速垂直上升a分钟后悬停在空中航拍,悬停5分钟后继续以原来的速度匀速垂直上升,到第8分钟时悬停在距地面150米处.乙无人机匀速垂直上升8分钟后停留在b米的高度,且第3分钟时和甲同在距地面60米处的位置.两台无人机的上升高度y(米)与时间x(分钟)的函数关系式如图所示.
(1)求b的值.
(2)求a的值及甲无人机上升时的速度.
(3)求乙无人机在甲无人机上方15米处时,x的值.
23.(本小题10分)
在平面直角坐标系xOy中,抛物线y=x2-2mx+m2与y轴交于点A,过点A作直线l垂直于y轴.
(1)求抛物线的对称轴.(用含m的式子表示)
(2)将抛物线在y轴右侧的部分沿直线l翻折,其余部分保持不变,形成图形G.M(x1,y1),N(x2,y2)为图形G上的两点.
①当m=0时,若x1<x2,判断y1与y2的大小关系,并说明理由.
②若对于x1=1,x2=2,都有y1>y2,直接写出m的取值范围.
24.(本小题12分)
如图1,在四边形ABCD中,∠BAD=∠BCD=90°,连接AC,AC=AD,E为AD的中点,连接BE,交AC于点F.
(1)求证:∠CAD=2∠ACB.
(2)如图2,若AD=CD,求的值.
(3)如图3,若BE⊥AC,求tan∠ACB.
1.【答案】C
2.【答案】A
3.【答案】C
4.【答案】B
5.【答案】D
6.【答案】B
7.【答案】D
8.【答案】A
9.【答案】D
10.【答案】A
11.【答案】(2x-1)2
12.【答案】-1≤x<3
13.【答案】60
14.【答案】3
15.【答案】-3
16.【答案】
17.【答案】-1.
18.【答案】无解.
19.【答案】45°;
线段MG的长为10.
20.【答案】9,8.8,8;
选甲更合适.理由见解答.
21.【答案】解:(1)由作图可知:AD平分∠BAC,
∴∠BAD=∠CAD.
∵CD∥AB,
∴∠ADC=∠BAD.
∴∠ADC=∠CAD.
∴CA=CD.
∵AC=4,
∴CD=4.
(2)由作图可知:PQ垂直平分AC,
∴FA=FC.
∵∠BAC=60°,
∴△ACF为等边三角形.
∴AF=AC=4.
∵AC=2AB,
∴AB=2.
∴BF=AF-AB=4-2=2.
由(1)知,CD=4,CD∥AB,
∴∠BFG=∠DCG,∠FBG=∠CDG.
∴△BFG∽△DCG.
∴.
22.【答案】160;
50米/分钟,1.2;
3.75或.
23.【答案】对称轴为直线x=m;
①y1>y2;
②m.
24.【答案】见解析;
;
.
第1页,共1页
一、选择题:本题共10小题,每小题3分,共30分。在每小题给出的选项中,只有一项是符合题目要求的。
1.下列实数中,无理数是( )
A. -2 B. 0 C. D.
2.下列几何体由5个相同的小正方体搭成,其左视图是( )
A.
B.
C.
D.
3.某校30个班级在学校“书香班级”的创建活动中,以班级为单位进行捐书,根据班级的捐书量制作下表:
数量/册 160 175 183 190 198 203 212 225
班级数 2 4 7 5 6 3 2 1
这组数据的众数和中位数分别是( )
A. 7,5.5 B. 7,5 C. 183,190 D. 183,194
4.如图,将一个正方形纸片沿图中虚线剪开,能拼成下列四个图形,其中是中心对称图形的是( )
A.
B.
C.
D.
5.下列运算正确的是( )
A. (-a3)2=-a6 B. a2 a3=a6 C. (a+b)2=a2+b2 D. 3a2-2a2=a2
6.某商场在五一期间推出促销活动,活动期间内,凡是购物即可参与抽奖.不透明的盒子里装有12张质地、大小完全相同的纸片,其中2张纸片写有奖品为“扫地机器人一台”,4张纸片写有奖品为“餐具一套”,6张纸片写有奖品为“纸巾一袋”.从盒中任意摸出1张纸片,摸出奖品为“扫地机器人一台”的概率是( )
A. B. C. D.
7.A,B,C,D四点在⊙O上的位置如图所示,∠OAB=10°,∠ABD=20°,则∠C的度数为( )
A. 130°
B. 120°
C. 110°
D. 100°
8.晚托期间,八(1)班学生积极参与文体活动.起初,篮球组的报名人数比羽毛球组报名人数的还多4人;后来,羽毛球组有8人改报了篮球组,此时,篮球组的报名人数是羽毛球组报名人数的2倍.设起初报名篮球组的人数为x,报名羽毛球组的人数为y,则下面所列方程组正确的是( )
A. B.
C. D.
9.二次函数y=(x+1)2+(x+2)2与y=(x+a)2+(x+b)2的图象关于y轴对称,则(a-1)2+(b-1)2的值为( )
A. 0 B. 1 C. 10 D. 13
10.在等边△ABC中,D为△ABC内的一点,∠BDC=120°,∠ADB=90°,CD=1,则AD的长为( )
A.
B. 2
C.
D. 3
二、填空题:本题共6小题,每小题3分,共18分。
11.因式分解:4x2-4x+1=______.
12.不等式组的解集为______.
13.如图,点F在正五边形的边ED上运动.若∠ABF=x°,写出一个符合条件的x的值:______.
14.如图,在 ABCD中,AB∥x轴,点A(1,2),B(7,2),D(0,1),反比例函数的图象在第一象限内经过点C,且与AB交于点E.则点E的横坐标为______.
15.定义:A(x,y)为平面直角坐标系内的点,若满足x=y,则把点A叫做“平衡点”,例如:M(1,1),N(-2,-2)都是“平衡点”.当-1≤x≤3时,直线y=2x+m上有“平衡点”,则m的最小值为______.
16.如图,在菱形ABCD中,分别过点A,C作AE∥CF,过点B,D作BG∥DH,交点分别为E,F,G,H.若G为AE的中点,∠AEH=∠ABC=60°,则四边形GEHF与四边形ABCD的面积之比为______.
三、解答题:本题共8小题,共72分。解答应写出文字说明,证明过程或演算步骤。
17.(本小题8分)
计算:.
18.(本小题8分)
解分式方程:.
19.(本小题8分)
司南是我国古代辨别方向用的一种仪器.其早在战国时期就已被发明,是现在所用指南针的始祖.如图1,司南中心为一圆形,圆心为点O,直径为20.根据八个方位将圆形八等分(图2中点A-H),过点E作⊙O的切线,与AG的延长线交于点M,连接EG.
(1)求∠AEG的值.
(2)求线段MG的长.
20.(本小题8分)
某校举办“十佳歌手”演唱比赛,五位评委进行现场打分,将甲、乙、丙三位选手的得分数据整理成下列统计图.根据以上信息,解答下列问题.
(1)完成表格:
平均数/分 中位数/分 众数/分 方差
甲 8.8 ①______ 8和9 0.56
乙 ②______ 9 9 0.96
丙 8.8 8 ③______ 0.96
(2)从三位选手中选一位参加市级比赛,你认为选谁更合适?请说明理由.
21.(本小题8分)
如图1,AC=2AB=4.以点A为圆心,适当长为半径画弧,分别交AB,AC于点M,N.分别以点M,N为圆心,以大于的长为半径画弧,两弧在∠BAC内交于点E.作射线AE.过点C作CD∥AB,交AE于点D.
(1)求CD的长;
(2)如图2,连接BD.分别以点A,C为圆心,大于的长为半径画弧,两弧交于点P,Q.作直线PQ,交AB的延长线于点F.连接CF,交BD于点G.当∠BAC=60°时,求的值.
22.(本小题10分)
目前,无人机航拍越来越多的应用于各种领域.现对甲、乙两台无人机同时开始操作,甲无人机先匀速垂直上升a分钟后悬停在空中航拍,悬停5分钟后继续以原来的速度匀速垂直上升,到第8分钟时悬停在距地面150米处.乙无人机匀速垂直上升8分钟后停留在b米的高度,且第3分钟时和甲同在距地面60米处的位置.两台无人机的上升高度y(米)与时间x(分钟)的函数关系式如图所示.
(1)求b的值.
(2)求a的值及甲无人机上升时的速度.
(3)求乙无人机在甲无人机上方15米处时,x的值.
23.(本小题10分)
在平面直角坐标系xOy中,抛物线y=x2-2mx+m2与y轴交于点A,过点A作直线l垂直于y轴.
(1)求抛物线的对称轴.(用含m的式子表示)
(2)将抛物线在y轴右侧的部分沿直线l翻折,其余部分保持不变,形成图形G.M(x1,y1),N(x2,y2)为图形G上的两点.
①当m=0时,若x1<x2,判断y1与y2的大小关系,并说明理由.
②若对于x1=1,x2=2,都有y1>y2,直接写出m的取值范围.
24.(本小题12分)
如图1,在四边形ABCD中,∠BAD=∠BCD=90°,连接AC,AC=AD,E为AD的中点,连接BE,交AC于点F.
(1)求证:∠CAD=2∠ACB.
(2)如图2,若AD=CD,求的值.
(3)如图3,若BE⊥AC,求tan∠ACB.
1.【答案】C
2.【答案】A
3.【答案】C
4.【答案】B
5.【答案】D
6.【答案】B
7.【答案】D
8.【答案】A
9.【答案】D
10.【答案】A
11.【答案】(2x-1)2
12.【答案】-1≤x<3
13.【答案】60
14.【答案】3
15.【答案】-3
16.【答案】
17.【答案】-1.
18.【答案】无解.
19.【答案】45°;
线段MG的长为10.
20.【答案】9,8.8,8;
选甲更合适.理由见解答.
21.【答案】解:(1)由作图可知:AD平分∠BAC,
∴∠BAD=∠CAD.
∵CD∥AB,
∴∠ADC=∠BAD.
∴∠ADC=∠CAD.
∴CA=CD.
∵AC=4,
∴CD=4.
(2)由作图可知:PQ垂直平分AC,
∴FA=FC.
∵∠BAC=60°,
∴△ACF为等边三角形.
∴AF=AC=4.
∵AC=2AB,
∴AB=2.
∴BF=AF-AB=4-2=2.
由(1)知,CD=4,CD∥AB,
∴∠BFG=∠DCG,∠FBG=∠CDG.
∴△BFG∽△DCG.
∴.
22.【答案】160;
50米/分钟,1.2;
3.75或.
23.【答案】对称轴为直线x=m;
①y1>y2;
②m.
24.【答案】见解析;
;
.
第1页,共1页
同课章节目录
