2024-2025学年吉林省长春市高新区尚德学校八年级(下)期中数学试卷(含答案)
文档属性
| 名称 | 2024-2025学年吉林省长春市高新区尚德学校八年级(下)期中数学试卷(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 146.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-24 10:41:36 | ||
图片预览



文档简介
2024-2025学年吉林省长春市高新区尚德学校八年级(下)期中数学试卷
一、选择题:本题共8小题,每小题3分,共24分。在每小题给出的选项中,只有一项是符合题目要求的。
1.下列各式中是分式的是( )
A. B. C. D. x+y
2.如果把分式中的x和y都扩大到原来的4倍,那么分式的值( )
A. 扩大到原来的2倍 B. 扩大到原来的4倍 C. 不变 D. 缩小到原来的
3.中国的deepseek在网上成为热搜和下载安装的榜首软件,要支持这些软件功能,需要芯片的支持.据报道deepseek的主要芯片为28nm,28nm相当于0.0000000028m,数据0.0000000028用科学记数法表示为( )
A. 2.8×10-9 B. 2.8×10-8 C. 2.8×10-7 D. 2.8×108
4.若点P(x-3,2x)在y轴上,则点P的坐标为( )
A. (0,6) B. (0,12) C. (6,0) D. (4,0)
5.若y与-3x成反比例,x与成正比例,则y与z成( )
A. 正比例 B. 反比例 C. 不成比例 D. 不能确定
6.点P(x,y)在直线y=-x+4上,坐标(x,y)是二元一次方程5x-6y=33的解,则点P的位置在( )
A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限
7.已知三点(x1,y1)、(x2,y2)、(x3,y3)均在双曲线y=上,且x1<x2<0<x3,则下列各式正确的是( )
A. y1<y2<y3 B. y3<y2<y1 C. y3<y1<y2 D. y2<y1<y3
8.如图,在平面直角坐标系中,△ABC的顶点坐标分别为A(1,1),B(3,1),C(2,2),当直线y=kx+3与△ABC有交点时,k的取值范围是( )
A.
B.
C.
D. -2≤k≤-
二、填空题:本题共6小题,每小题3分,共18分。
9.函数y=中自变量x的取值范围是______.
10.若关于x的方程有增根,则a的值是______.
11.已知AB∥y轴,A的坐标为(1,6),AB=4,则点B的坐标是______.
12.将直线y=mx+2向右平移4个单位平移后的直线经过点(3,-4),则m= ______.
13.如图,A是反比例函数的图象上一点,AB⊥y轴于点B,点C与点B关于x轴对称,连接AC.若△ABC的面积为8,则k的值为______.
14.如图,函数y=kx+b(k,b为常数,k≠0)的图象经过点B(2,0),与函数y=2x的图象交于点A,下列结论:①点A的横坐标为2;②关于x的不等式kx+b<0的解集为x>2;③关于x的方程kx+b=2x的解为x=2;④关于x的不等式组0<kx+b<2x的解集为1<x<2.其中正确的是______(只填写序号).
三、计算题:本大题共1小题,共6分。
15.先化简,再求值:(1-)÷,其中x=3.
四、解答题:本题共9小题,共72分。解答应写出文字说明,证明过程或演算步骤。
16.(本小题5分)
计算.
17.(本小题8分)
解下列分式方程:
(1);
(2).
18.(本小题6分)
为建设美丽中国,各地从2023年开始通过建造小而美的“口袋公园”来提升人民群众的幸福感.为此某地绿化部门现需要购买A、B两种绿植,已知A种绿植单价是B种绿植单价的3倍,用6750元购买的A种绿植比用3000元购买的B种绿植少50株.求B种绿植单价.
19.(本小题7分)
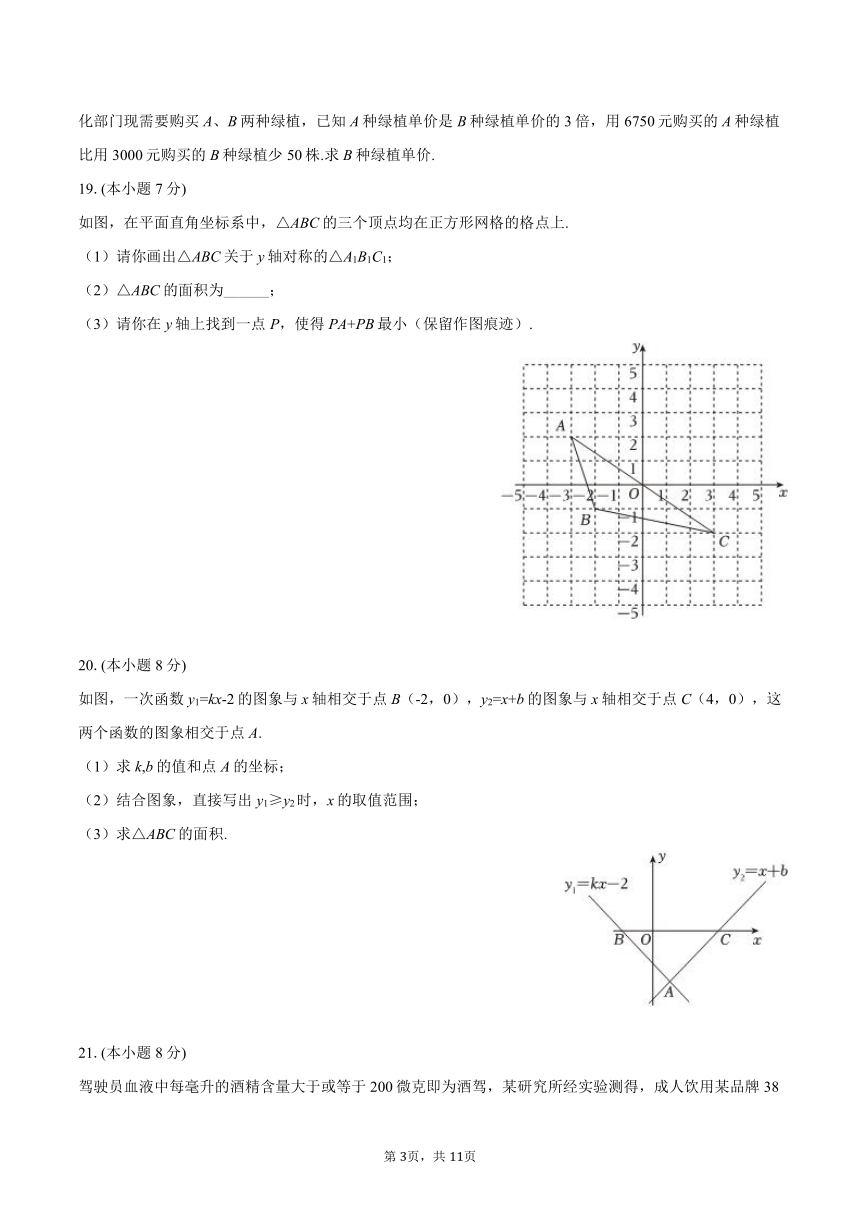
如图,在平面直角坐标系中,△ABC的三个顶点均在正方形网格的格点上.
(1)请你画出△ABC关于y轴对称的△A1B1C1;
(2)△ABC的面积为______;
(3)请你在y轴上找到一点P,使得PA+PB最小(保留作图痕迹).
20.(本小题8分)
如图,一次函数y1=kx-2的图象与x轴相交于点B(-2,0),y2=x+b的图象与x轴相交于点C(4,0),这两个函数的图象相交于点A.
(1)求k,b的值和点A的坐标;
(2)结合图象,直接写出y1≥y2时,x的取值范围;
(3)求△ABC的面积.
21.(本小题8分)
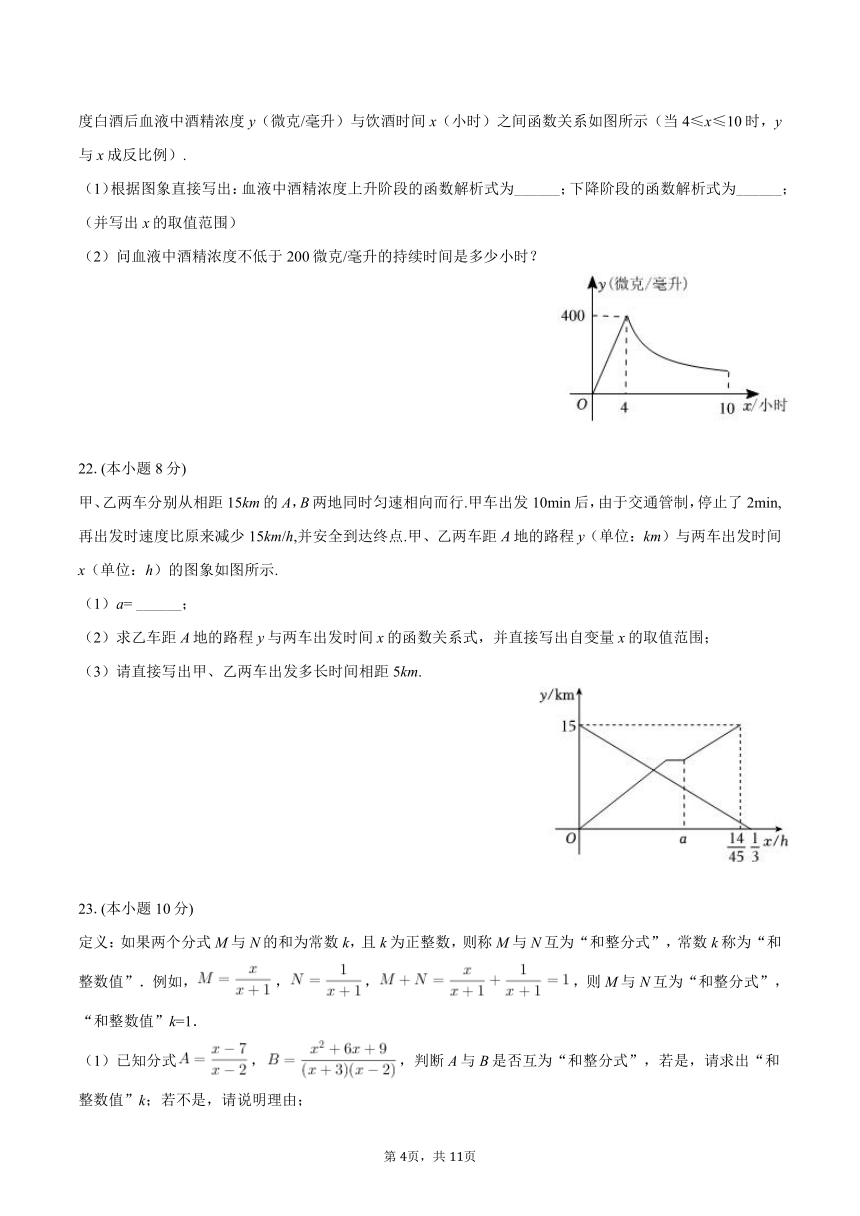
驾驶员血液中每毫升的酒精含量大于或等于200微克即为酒驾,某研究所经实验测得,成人饮用某品牌38度白酒后血液中酒精浓度y(微克/毫升)与饮酒时间x(小时)之间函数关系如图所示(当4≤x≤10时,y与x成反比例).
(1)根据图象直接写出:血液中酒精浓度上升阶段的函数解析式为______;下降阶段的函数解析式为______;(并写出x的取值范围)
(2)问血液中酒精浓度不低于200微克/毫升的持续时间是多少小时?
22.(本小题8分)
甲、乙两车分别从相距15km的A,B两地同时匀速相向而行.甲车出发10min后,由于交通管制,停止了2min,再出发时速度比原来减少15km/h,并安全到达终点.甲、乙两车距A地的路程y(单位:km)与两车出发时间x(单位:h)的图象如图所示.
(1)a= ______;
(2)求乙车距A地的路程y与两车出发时间x的函数关系式,并直接写出自变量x的取值范围;
(3)请直接写出甲、乙两车出发多长时间相距5km.
23.(本小题10分)
定义:如果两个分式M与N的和为常数k,且k为正整数,则称M与N互为“和整分式”,常数k称为“和整数值”.例如,,,,则M与N互为“和整分式”,“和整数值”k=1.
(1)已知分式,,判断A与B是否互为“和整分式”,若是,请求出“和整数值”k;若不是,请说明理由;
(2)已知分式,,C与D互为“和整分式”,且“和整数值”k=3.
①求P所代表的代数式;
②若分式D的值为正整数,求正整数x的值.
24.(本小题12分)
【概念引入】对于给定的一次函数y=kx+b(其中k,b为常数,且k≠0),则称函数为一次函数y=kx+b的伴随函数.
例如:一次函数y=3x-4,它的伴随函数为.
【理解运用】(1)对于一次函数y=2x+2,写出它的伴随函数的表达式.
(2)为了研究函数y=2x+2的伴随函数的图象某位同学制作了如下表格:
x … -2 -1 0 1 2 …
y … -2 ______ 2 0 ______ …
①补全表格中横线部分的数据,并根据表中的结果在图1所给的坐标系中画出函数y=2x+2的伴随函数的图象;
②已知直线y=x-1与y=2x+2的伴随函数的图象交于A,B两点(点A在点B的下方),点P(0,m)在y轴上,当△ABP的面积为8时,求m的值.
【拓展提升】(3)在平面直角坐标系中,点M,N的坐标分别为(-1,-4),(2,-2),连接MN,当一次函数y=2x+b的伴随函数的图象与线段MN的交点有且只有1个时,直接写出b的取值范围.
1.【答案】C
2.【答案】B
3.【答案】A
4.【答案】A
5.【答案】A
6.【答案】D
7.【答案】D
8.【答案】D
9.【答案】x≠3
10.【答案】-4
11.【答案】(1,10)或(1,2)
12.【答案】6
13.【答案】-8
14.【答案】②④
15.【答案】解:原式=()÷
=
=,
当x=3时,
原式=.
16.【答案】7.
17.【答案】无解;
x=3.
18.【答案】B种绿植单价是15元.
19.【答案】△ABC关于y轴对称的△A1B1C1,如图1即为所求;
;
7;
在y轴上使得PA+PB最小的点P,如图2即为所求.
20.【答案】k=-1,b=-4,点A的坐标为(1,-3);
x≤1;
△ABC的面积为9.
21.【答案】解:(1)y=100x(0≤x≤4); y=(4≤x≤10);
(2)当y=200,则200=100x,
解得:x=2,
当y=200,则200=,
解得:x=8,
∵8-2=6(小时),
∴血液中药物浓度不低于200微克/毫升的持续时间为6小时.
22.【答案】; y=-45x+15(0≤x≤); h或h.
23.【答案】解:(1)A与B互为“和整分式”,理由如下:
=
=
=
=
=2,
∴A与B互为“和整分式”,“和整数值”k=2;
(2)①,
∵C与D互为“和整分式”,且“和整数值”k=3,
∴,即3x2+2x-8+P=3(x+2)(x-2),
∴P=3(x2-4)-(3x2+2x-8)=-2x-4;
②∵,
若分式D的值为正整数,
∴x-2=-1或x-2=-2,
解得x=1或x=0,
∴正整数x的值为1.
24.【答案】(1);
(2)①当x=-1时,y=2x+2=2×(-1)+2=0,当x=2时,y=-2x+2=-2×2+2=-2,
∴补全表格如下:
x … -2 -1 0 1 2 …
y … -2 0 2 0 -2 …
根据表中的结果在图1所给的坐标系中画出函数y=2x+2的伴随函数的图象,如图1即为所求,
故答案为:0;-2;
②如图2,
联立得:,
解得,
∴A(-3,-4);
联立得:,
解得,
∴B(1,0).
当x=0时,y=x-1=0-1=-1,
∴y=x-1与y轴的交点为H(0,-1),
∵点P(0,m),
∴PH=|m+1|,
∵△ABP的面积为8,
∴S△BPH+S△APH=8,即,
解得m=3或m=-5;
(3)-2<b≤2或者.
第1页,共1页
一、选择题:本题共8小题,每小题3分,共24分。在每小题给出的选项中,只有一项是符合题目要求的。
1.下列各式中是分式的是( )
A. B. C. D. x+y
2.如果把分式中的x和y都扩大到原来的4倍,那么分式的值( )
A. 扩大到原来的2倍 B. 扩大到原来的4倍 C. 不变 D. 缩小到原来的
3.中国的deepseek在网上成为热搜和下载安装的榜首软件,要支持这些软件功能,需要芯片的支持.据报道deepseek的主要芯片为28nm,28nm相当于0.0000000028m,数据0.0000000028用科学记数法表示为( )
A. 2.8×10-9 B. 2.8×10-8 C. 2.8×10-7 D. 2.8×108
4.若点P(x-3,2x)在y轴上,则点P的坐标为( )
A. (0,6) B. (0,12) C. (6,0) D. (4,0)
5.若y与-3x成反比例,x与成正比例,则y与z成( )
A. 正比例 B. 反比例 C. 不成比例 D. 不能确定
6.点P(x,y)在直线y=-x+4上,坐标(x,y)是二元一次方程5x-6y=33的解,则点P的位置在( )
A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限
7.已知三点(x1,y1)、(x2,y2)、(x3,y3)均在双曲线y=上,且x1<x2<0<x3,则下列各式正确的是( )
A. y1<y2<y3 B. y3<y2<y1 C. y3<y1<y2 D. y2<y1<y3
8.如图,在平面直角坐标系中,△ABC的顶点坐标分别为A(1,1),B(3,1),C(2,2),当直线y=kx+3与△ABC有交点时,k的取值范围是( )
A.
B.
C.
D. -2≤k≤-
二、填空题:本题共6小题,每小题3分,共18分。
9.函数y=中自变量x的取值范围是______.
10.若关于x的方程有增根,则a的值是______.
11.已知AB∥y轴,A的坐标为(1,6),AB=4,则点B的坐标是______.
12.将直线y=mx+2向右平移4个单位平移后的直线经过点(3,-4),则m= ______.
13.如图,A是反比例函数的图象上一点,AB⊥y轴于点B,点C与点B关于x轴对称,连接AC.若△ABC的面积为8,则k的值为______.
14.如图,函数y=kx+b(k,b为常数,k≠0)的图象经过点B(2,0),与函数y=2x的图象交于点A,下列结论:①点A的横坐标为2;②关于x的不等式kx+b<0的解集为x>2;③关于x的方程kx+b=2x的解为x=2;④关于x的不等式组0<kx+b<2x的解集为1<x<2.其中正确的是______(只填写序号).
三、计算题:本大题共1小题,共6分。
15.先化简,再求值:(1-)÷,其中x=3.
四、解答题:本题共9小题,共72分。解答应写出文字说明,证明过程或演算步骤。
16.(本小题5分)
计算.
17.(本小题8分)
解下列分式方程:
(1);
(2).
18.(本小题6分)
为建设美丽中国,各地从2023年开始通过建造小而美的“口袋公园”来提升人民群众的幸福感.为此某地绿化部门现需要购买A、B两种绿植,已知A种绿植单价是B种绿植单价的3倍,用6750元购买的A种绿植比用3000元购买的B种绿植少50株.求B种绿植单价.
19.(本小题7分)
如图,在平面直角坐标系中,△ABC的三个顶点均在正方形网格的格点上.
(1)请你画出△ABC关于y轴对称的△A1B1C1;
(2)△ABC的面积为______;
(3)请你在y轴上找到一点P,使得PA+PB最小(保留作图痕迹).
20.(本小题8分)
如图,一次函数y1=kx-2的图象与x轴相交于点B(-2,0),y2=x+b的图象与x轴相交于点C(4,0),这两个函数的图象相交于点A.
(1)求k,b的值和点A的坐标;
(2)结合图象,直接写出y1≥y2时,x的取值范围;
(3)求△ABC的面积.
21.(本小题8分)
驾驶员血液中每毫升的酒精含量大于或等于200微克即为酒驾,某研究所经实验测得,成人饮用某品牌38度白酒后血液中酒精浓度y(微克/毫升)与饮酒时间x(小时)之间函数关系如图所示(当4≤x≤10时,y与x成反比例).
(1)根据图象直接写出:血液中酒精浓度上升阶段的函数解析式为______;下降阶段的函数解析式为______;(并写出x的取值范围)
(2)问血液中酒精浓度不低于200微克/毫升的持续时间是多少小时?
22.(本小题8分)
甲、乙两车分别从相距15km的A,B两地同时匀速相向而行.甲车出发10min后,由于交通管制,停止了2min,再出发时速度比原来减少15km/h,并安全到达终点.甲、乙两车距A地的路程y(单位:km)与两车出发时间x(单位:h)的图象如图所示.
(1)a= ______;
(2)求乙车距A地的路程y与两车出发时间x的函数关系式,并直接写出自变量x的取值范围;
(3)请直接写出甲、乙两车出发多长时间相距5km.
23.(本小题10分)
定义:如果两个分式M与N的和为常数k,且k为正整数,则称M与N互为“和整分式”,常数k称为“和整数值”.例如,,,,则M与N互为“和整分式”,“和整数值”k=1.
(1)已知分式,,判断A与B是否互为“和整分式”,若是,请求出“和整数值”k;若不是,请说明理由;
(2)已知分式,,C与D互为“和整分式”,且“和整数值”k=3.
①求P所代表的代数式;
②若分式D的值为正整数,求正整数x的值.
24.(本小题12分)
【概念引入】对于给定的一次函数y=kx+b(其中k,b为常数,且k≠0),则称函数为一次函数y=kx+b的伴随函数.
例如:一次函数y=3x-4,它的伴随函数为.
【理解运用】(1)对于一次函数y=2x+2,写出它的伴随函数的表达式.
(2)为了研究函数y=2x+2的伴随函数的图象某位同学制作了如下表格:
x … -2 -1 0 1 2 …
y … -2 ______ 2 0 ______ …
①补全表格中横线部分的数据,并根据表中的结果在图1所给的坐标系中画出函数y=2x+2的伴随函数的图象;
②已知直线y=x-1与y=2x+2的伴随函数的图象交于A,B两点(点A在点B的下方),点P(0,m)在y轴上,当△ABP的面积为8时,求m的值.
【拓展提升】(3)在平面直角坐标系中,点M,N的坐标分别为(-1,-4),(2,-2),连接MN,当一次函数y=2x+b的伴随函数的图象与线段MN的交点有且只有1个时,直接写出b的取值范围.
1.【答案】C
2.【答案】B
3.【答案】A
4.【答案】A
5.【答案】A
6.【答案】D
7.【答案】D
8.【答案】D
9.【答案】x≠3
10.【答案】-4
11.【答案】(1,10)或(1,2)
12.【答案】6
13.【答案】-8
14.【答案】②④
15.【答案】解:原式=()÷
=
=,
当x=3时,
原式=.
16.【答案】7.
17.【答案】无解;
x=3.
18.【答案】B种绿植单价是15元.
19.【答案】△ABC关于y轴对称的△A1B1C1,如图1即为所求;
;
7;
在y轴上使得PA+PB最小的点P,如图2即为所求.
20.【答案】k=-1,b=-4,点A的坐标为(1,-3);
x≤1;
△ABC的面积为9.
21.【答案】解:(1)y=100x(0≤x≤4); y=(4≤x≤10);
(2)当y=200,则200=100x,
解得:x=2,
当y=200,则200=,
解得:x=8,
∵8-2=6(小时),
∴血液中药物浓度不低于200微克/毫升的持续时间为6小时.
22.【答案】; y=-45x+15(0≤x≤); h或h.
23.【答案】解:(1)A与B互为“和整分式”,理由如下:
=
=
=
=
=2,
∴A与B互为“和整分式”,“和整数值”k=2;
(2)①,
∵C与D互为“和整分式”,且“和整数值”k=3,
∴,即3x2+2x-8+P=3(x+2)(x-2),
∴P=3(x2-4)-(3x2+2x-8)=-2x-4;
②∵,
若分式D的值为正整数,
∴x-2=-1或x-2=-2,
解得x=1或x=0,
∴正整数x的值为1.
24.【答案】(1);
(2)①当x=-1时,y=2x+2=2×(-1)+2=0,当x=2时,y=-2x+2=-2×2+2=-2,
∴补全表格如下:
x … -2 -1 0 1 2 …
y … -2 0 2 0 -2 …
根据表中的结果在图1所给的坐标系中画出函数y=2x+2的伴随函数的图象,如图1即为所求,
故答案为:0;-2;
②如图2,
联立得:,
解得,
∴A(-3,-4);
联立得:,
解得,
∴B(1,0).
当x=0时,y=x-1=0-1=-1,
∴y=x-1与y轴的交点为H(0,-1),
∵点P(0,m),
∴PH=|m+1|,
∵△ABP的面积为8,
∴S△BPH+S△APH=8,即,
解得m=3或m=-5;
(3)-2<b≤2或者.
第1页,共1页
同课章节目录
