第3章 对圆的进一步认识(图片版,无答案)初中数学青岛版(2024)九年级上
文档属性
| 名称 | 第3章 对圆的进一步认识(图片版,无答案)初中数学青岛版(2024)九年级上 |  | |
| 格式 | |||
| 文件大小 | 7.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-24 18:08:24 | ||
图片预览


文档简介
1相交弦定理
结诊及技巧。
如图,在⊙O中,弦AB和弦CD如图,连接AD,BC
相交于点E,则'CE,DEAE:BE
∠A=∠C,LB=∠D,
.△CBE∽△ADE.
0
CE BE
0
AE DE
.CE·DE=AE·BE
交的的长度时
例题
如图,BP=2,PD=3,△ABD的面积为12.5,AC⊥BD,则PC的长为
》分析弦AC,BD相交于点P,可使用相交弦定理.先根据△ABD的面积及底边BD的长,
求高AP的长,然后根据相交弦定理PC·PA=BP·PD,代入求出PC的长即可.
详解:BP=2,PD=3,∴.BD=BP+PD=2+3=5
ACLBD,△ABD的面积为12.5,即SAm号BD·PA=125.
12.5=}×5×P4,解得P4=5.
根据相交弦定理可知,PC·PA=PB·PD,
·PCx5=2x3,解得PC=
1
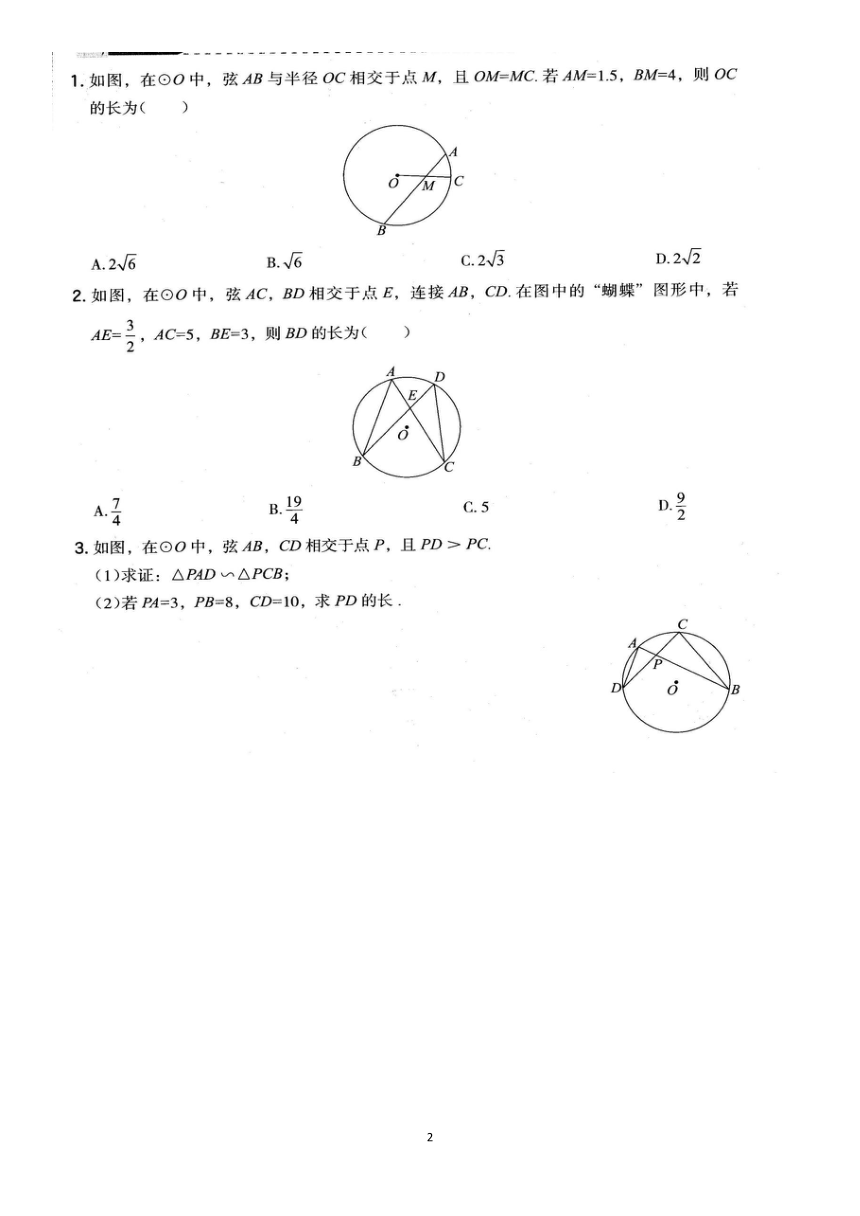
1.如图,在⊙O中,弦AB与半径OC相交于点M,且OM=MC.若AM=1.5,BM=4,则OC
的长为()
A.26
B.6
C.23
D.2√2
2.如图,在⊙O巾,弦AC,BD相交于点E,连接AB,CD.在图中的“蝴蝶”图形中,若
AE=号,AC=5,BE=3,则BD的长为(
)
A.
B.9
C.5
3.如图,在⊙O中,弦AB,CD相交于点P,且PD>PC
(1)求证:△PAD∽△PCB;
(2)若PA=3,PB=8,CD=10,求PD的长.
2
2割线定理
结论及技巧港
清楚拉明过程
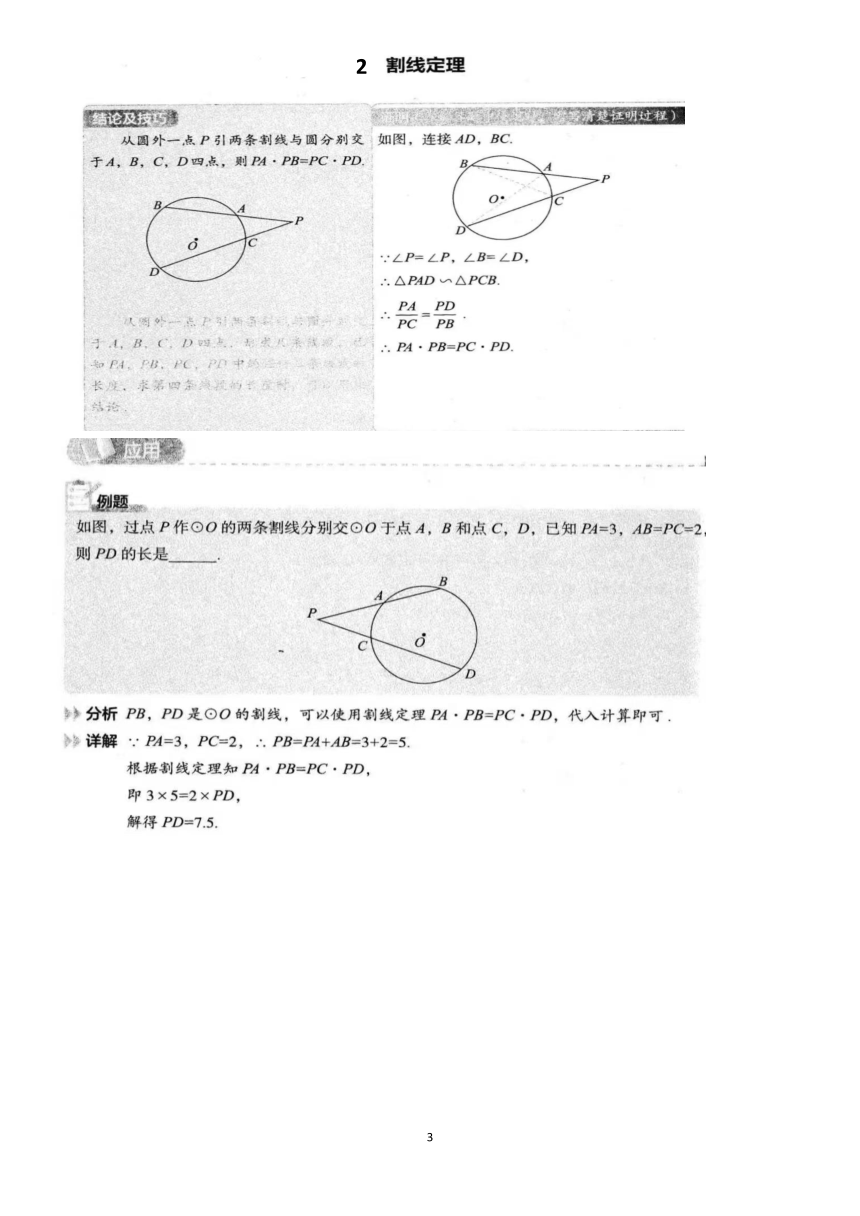
从圆外一点P引两条割线与圆分别交如图,连接AD,BC
于A,B,C,D四点,则PA·PB=PC·PD
0
B
D
∠P=∠P,∠B=∠D,
∴.△PAD∽△PCB.
是阳
于L,B(C,D时点,大来
.PA·PB=PC·PD
知P,PB,PC,P中泰
长度,求第四条的。
结论
成用
。列题
如图,过点P作⊙O的两条割线分别交⊙O于点A,B和点C,D,已知PA=3,AB=PC=2,
则PD的长是
分析PB,PD是⊙O的割线,可以使用割线定理PA·PB=PC·PD,代入计算即可
》详解PA=3,PC=2,.PB=PA+AB=3+2=5.
根据割线定理知PA·PB=PC·PD,
即3×5=2×PD,
解得PD=7.5.
3
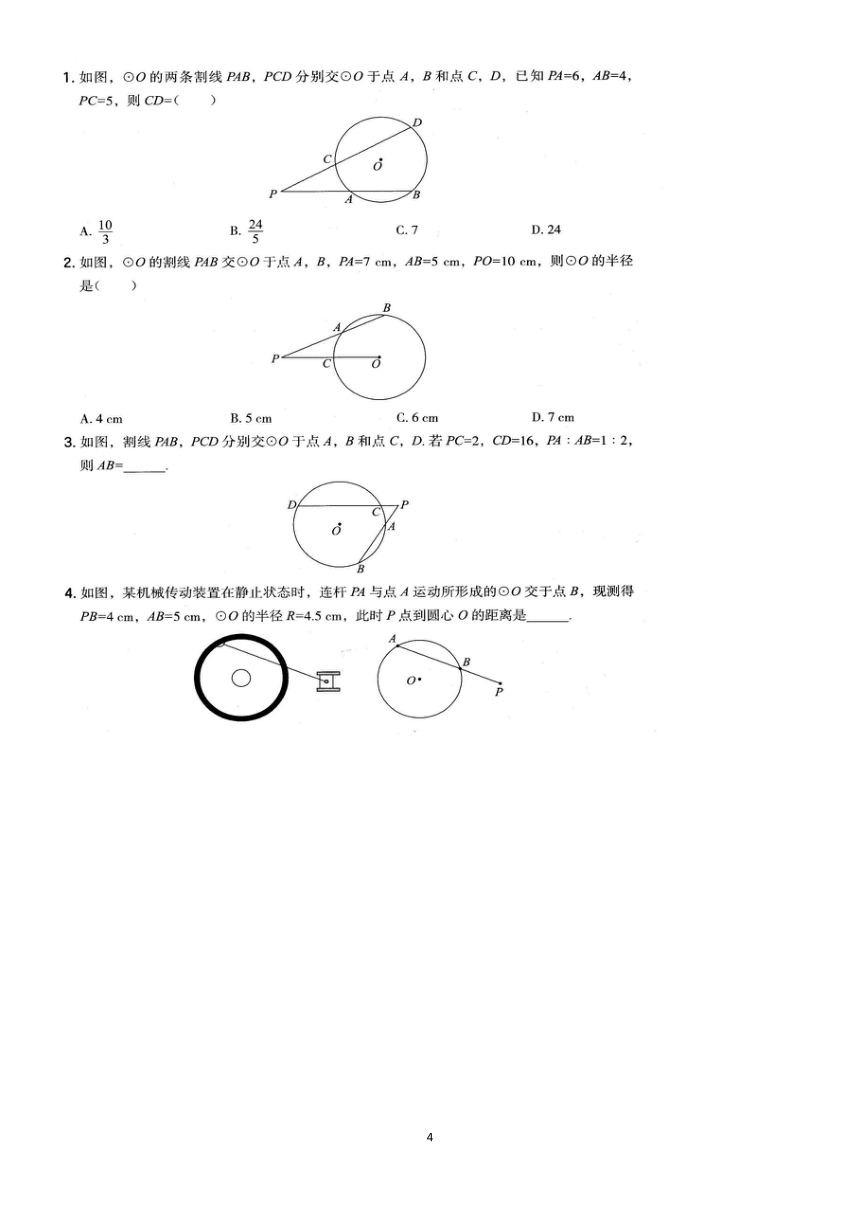
1.如图,⊙O的两条割线PAB,PCD分别交⊙O于点A,B和点C,D,已知A=6,AB=4,
PC-5,则CD=()
B
A.I
B.
C.7
D.24
2.如图,⊙O的割线PAB交⊙O于点A,B,PA=7cm,AB-5cn,PO=10cm,则⊙O的半径
是()
A.4cm
B.5 cm
C.6 cm
D.7 cm
3.如图,割线PAB,PCD分别交⊙O于点A,B和点C,D.若PC=2,CD=16,PA:AB=1:2,
则AB=一·
B
4.如图,某机械传动装置在静止状态时,连杆A与点A运动所形成的⊙O交于点B,现测得
PB=4cm,AB=5cm,⊙O的半径R=4.5cm,此时P点到圆心O的距离是
A
0"
结诊及技巧。
如图,在⊙O中,弦AB和弦CD如图,连接AD,BC
相交于点E,则'CE,DEAE:BE
∠A=∠C,LB=∠D,
.△CBE∽△ADE.
0
CE BE
0
AE DE
.CE·DE=AE·BE
交的的长度时
例题
如图,BP=2,PD=3,△ABD的面积为12.5,AC⊥BD,则PC的长为
》分析弦AC,BD相交于点P,可使用相交弦定理.先根据△ABD的面积及底边BD的长,
求高AP的长,然后根据相交弦定理PC·PA=BP·PD,代入求出PC的长即可.
详解:BP=2,PD=3,∴.BD=BP+PD=2+3=5
ACLBD,△ABD的面积为12.5,即SAm号BD·PA=125.
12.5=}×5×P4,解得P4=5.
根据相交弦定理可知,PC·PA=PB·PD,
·PCx5=2x3,解得PC=
1
1.如图,在⊙O中,弦AB与半径OC相交于点M,且OM=MC.若AM=1.5,BM=4,则OC
的长为()
A.26
B.6
C.23
D.2√2
2.如图,在⊙O巾,弦AC,BD相交于点E,连接AB,CD.在图中的“蝴蝶”图形中,若
AE=号,AC=5,BE=3,则BD的长为(
)
A.
B.9
C.5
3.如图,在⊙O中,弦AB,CD相交于点P,且PD>PC
(1)求证:△PAD∽△PCB;
(2)若PA=3,PB=8,CD=10,求PD的长.
2
2割线定理
结论及技巧港
清楚拉明过程
从圆外一点P引两条割线与圆分别交如图,连接AD,BC
于A,B,C,D四点,则PA·PB=PC·PD
0
B
D
∠P=∠P,∠B=∠D,
∴.△PAD∽△PCB.
是阳
于L,B(C,D时点,大来
.PA·PB=PC·PD
知P,PB,PC,P中泰
长度,求第四条的。
结论
成用
。列题
如图,过点P作⊙O的两条割线分别交⊙O于点A,B和点C,D,已知PA=3,AB=PC=2,
则PD的长是
分析PB,PD是⊙O的割线,可以使用割线定理PA·PB=PC·PD,代入计算即可
》详解PA=3,PC=2,.PB=PA+AB=3+2=5.
根据割线定理知PA·PB=PC·PD,
即3×5=2×PD,
解得PD=7.5.
3
1.如图,⊙O的两条割线PAB,PCD分别交⊙O于点A,B和点C,D,已知A=6,AB=4,
PC-5,则CD=()
B
A.I
B.
C.7
D.24
2.如图,⊙O的割线PAB交⊙O于点A,B,PA=7cm,AB-5cn,PO=10cm,则⊙O的半径
是()
A.4cm
B.5 cm
C.6 cm
D.7 cm
3.如图,割线PAB,PCD分别交⊙O于点A,B和点C,D.若PC=2,CD=16,PA:AB=1:2,
则AB=一·
B
4.如图,某机械传动装置在静止状态时,连杆A与点A运动所形成的⊙O交于点B,现测得
PB=4cm,AB=5cm,⊙O的半径R=4.5cm,此时P点到圆心O的距离是
A
0"
同课章节目录
- 第1章 图形的相似
- 1.1 相似多边形
- 1.2 怎样判定三角形相似
- 1.3 相似三角形的性质
- 1.4 图形的位似
- 第2章 解直角三角形
- 2.1 锐角三角比
- 2.2 30°,45°,60°角的三角比
- 2.3 用计算器求锐角三角比
- 2.4 解直角三角形
- 2.5 解直角三角形的应用
- 第3章 对圆的进一步认识
- 3.1 圆的对称性
- 3.2 确定圆的条件
- 3.3 圆周角
- 3.4 直线与圆的位置关系
- 3.5 三角形的内切圆
- 3.6 弧长及扇形面积的计算
- 3.7 正多边形与圆
- 课题学习 图形变换与图案设计
- 第4章 一元二次方程
- 4.1 一元二次方程
- 4.2 用配方法解一元二次方程
- 4.3 用公式法解一元二次方程
- 4.4 用因式分解法解一元二次方程
- 4.5 一元二次方程的应用
- 4.6 一元二次方程根与系数的关系
