2024-2025学年广东省肇庆市七年级(上)期末数学模拟试卷(含答案)
文档属性
| 名称 | 2024-2025学年广东省肇庆市七年级(上)期末数学模拟试卷(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 141.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-24 18:57:14 | ||
图片预览



文档简介
2024-2025学年广东省肇庆市七年级(上)期末数学模拟试卷
一、选择题:本题共10小题,每小题3分,共30分。在每小题给出的选项中,只有一项是符合题目要求的。
1.如果+50m表示向东走50m,那么向西走40m表示为( )
A. -50m B. -40m C. +40m D. +50m
2.若8xmy与6x3yn的和是单项式,则m+n的值为( )
A. 4 B. 8 C. -4 D. -8
3.根据文旅部的数据,2023年国庆假期前七天,国内出游人数达到7.54亿人次,旅游收入6630.9亿元.基本恢复甚至超越2019年同期统计,这是一个令人振奋的数据.其中数据6630.9亿用科学记数法表示为( )
A. 6.6309×108 B. 6.6309×109 C. 6.6309×1010 D. 6.6309×1011
4.如图是由若干个完全相同的小正方体组成的几何体,若从左面看这个几何体,则看到的平面图形是( )
A.
B.
C.
D.
5.式子a-(b-c+d)去括号的正确结果是( )
A. a+b+c+d B. a+b-c+d C. a-b-c+d D. a-b+c-d
6.在下列方程的变形中,正确的是( )
A. 由2x=-3得 B. 由得x=2
C. 由4x-3=3x得4x-3x=3 D. 由于得x=2
7.下列说法中,不正确的是( )
A. 零是绝对值最小的数 B. 倒数等于本身的数只有1
C. 相反数等于本身的数只有0 D. 原点左边的数离原点越远就越小
8.在数轴上表示a、b两数的点如图所示,则下列判断正确的是( )
A. ab>0 B. a+b>0 C. a+b<0 D. |a|>|b|
9.有一东西向的直线吊桥横跨溪谷,小维、阿良分别从西桥头、东桥头同时开始往吊桥的另一头笔直地走过去,如图所示,已知小维从西桥头走了84步,阿良从东桥头走了60步时,两人在吊桥上的某点交会,且交会之后阿良再走70步恰好走到西桥头,若小维每步的距离相等,阿良每步的距离相等,则交会之后小维再走多少步会恰好走到东桥头( )
A. 46 B. 50 C. 60 D. 72
10.点P在线段EF上,现有四个等式①PE=PF;②PE=EF;③EF=2PE;④2PE=EF;其中能表示点P是EF中点的有( )
A. 4个 B. 3个 C. 2个 D. 1个
二、填空题:本题共5小题,每小题3分,共15分。
11.方程2x=6的解是______.
12.某地某天的最高气温为3℃,最低气温为-8℃,这天的温差是______℃.
13.如图,C为线段AB上一点,D为线段BC的中点,AB=20,AD=14,则AC的长为______.
14.若m,n互为相反数,p,q互为倒数,则=______.
15.已知关于x的一元一次方程x+3=2x+b的解为x=2,那么关于y的一元一次方程(y+1)+3=2(y+1)+b的解为y= ______.
三、解答题:本题共9小题,共75分。解答应写出文字说明,证明过程或演算步骤。
16.(本小题8分)
计算:
(1)12-(-18)+(-7)-|-15|;
(2).
17.(本小题8分)
(1)列方程求解:把一些图书分给某班学生阅读,如果每人分3本,则剩余20本;如果每人分4本,则还缺25本.问这个班有多少学生?这些图书共有多少本?
(2)列方程求解:一个角的余角比这个角的补角的三分之一多6°,求这个角的大小.
18.(本小题8分)
解下列方程:
(1)3x+3=2x+7;
(2).
19.(本小题7分)
化简:
(1)x3-2x2-x3+5x2+4;
(2).
20.(本小题9分)
已知一个三角形的第一条边长为3a+b,第二条边比第一条边短a-2b,第三条边比第二条边长2a+b.
(1)则第二边的边长为______,第三条边的边长为______;
(2)用含a,b的式子表示这个三角形的周长,并化简;
(3)若a,b满足|a-8|+(b-7)2=0,求这个三角形的周长.
21.(本小题11分)
如图,点A在点O的北偏西60°的方向上,点B在点O的南偏东20°的方向上,OE平分∠AOB.求∠AOB和∠DOE的度数.
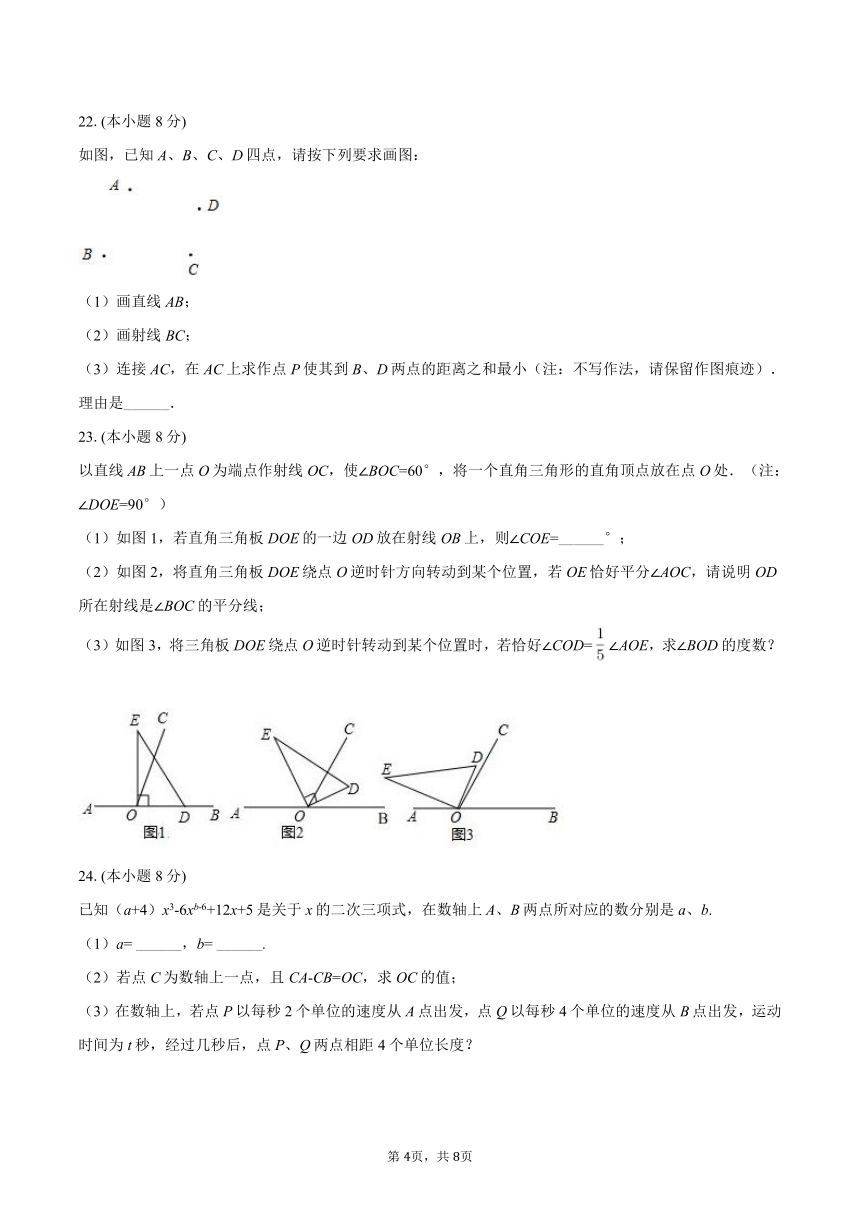
22.(本小题8分)
如图,已知A、B、C、D四点,请按下列要求画图:
(1)画直线AB;
(2)画射线BC;
(3)连接AC,在AC上求作点P使其到B、D两点的距离之和最小(注:不写作法,请保留作图痕迹).
理由是______.
23.(本小题8分)
以直线AB上一点O为端点作射线 OC,使∠BOC=60°,将一个直角三角形的直角顶点放在点O处.(注:∠DOE=90°)
(1)如图1,若直角三角板DOE的一边OD放在射线OB上,则∠COE=______°;
(2)如图2,将直角三角板DOE绕点O逆时针方向转动到某个位置,若OE恰好平分∠AOC,请说明OD所在射线是∠BOC的平分线;
(3)如图3,将三角板DOE绕点O逆时针转动到某个位置时,若恰好∠COD=∠AOE,求∠BOD的度数?
24.(本小题8分)
已知(a+4)x3-6xb-6+12x+5是关于x的二次三项式,在数轴上A、B两点所对应的数分别是a、b.
(1)a= ______,b= ______.
(2)若点C为数轴上一点,且CA-CB=OC,求OC的值;
(3)在数轴上,若点P以每秒2个单位的速度从A点出发,点Q以每秒4个单位的速度从B点出发,运动时间为t秒,经过几秒后,点P、Q两点相距4个单位长度?
1.【答案】B
2.【答案】A
3.【答案】D
4.【答案】D
5.【答案】D
6.【答案】C
7.【答案】B
8.【答案】C
9.【答案】D
10.【答案】B
11.【答案】x=3
12.【答案】11
13.【答案】8
14.【答案】
15.【答案】1
16.【答案】8;
55.
17.【答案】这个班有45名学生,图书有155本;
这个角是36°.
18.【答案】解:(1)3x+3=2x+7,
移项得:3x-2x=7-3,
合并同类项得:x=4;
(2),
去分母得:2(2x-1)-(10x+1)=3(2x+1)-12,
去括号得:4x-2-10x-1=6x+3-12,
移项,合并同类项得:-12x=-6,
未知数系数化为1得:.
19.【答案】3x2+4;
a2+a-2.
20.【答案】(1)2a+3b ;4a+4b;
(2)该三角形的周长为:(3a+b)+(2a+3b)+(4a+4b)
=3a+b+2a+3b+4a+4b
=9a+8b.
(3)由题意可知:a=8,b=7,
该三角形的周长为:9×8+8×7=128.
21.【答案】解:由题意得:∠AOC=90°-60°=30°,
∴∠AOB=30°+90°+20°=140°,
∵OE平分∠AOB,
∴,
∴∠DOE=∠EOB-∠DOB=50°,
∴∠AOB=140°,∠DOE=50°.
22.【答案】解:(1)如图,直线AB即为所作;
(2)如图,射线BC即为所作;
(3)如图,点P即为所求作的点.理由是:两点之间线段最短.
故答案为:两点之间线段最短.
23.【答案】解:(1)30;
(2)∵OE平分∠AOC,
∴∠COE=∠AOE=COA,
∵∠EOD=90°,
∴∠AOE+∠DOB=90°,∠COE+∠COD=90°,
∴∠COD=∠DOB,
∴OD所在射线是∠BOC的平分线;
(3)设∠COD=x°,则∠AOE=5x°,
∵∠DOE=90°,∠BOC=60°,
当OD边在∠AOC之间时,
6x=30,
解得x=5;
当OD边在∠BOC之间时,
5x+90-x=120,
解得x=7.5,
即∠COD=5°或7.5°,
∴∠BOD=∠COD+∠BOC=65°
或∠BOD=∠BOC-∠COD=52.5°.
24.【答案】(1)-4,8.
(2)由CA-CB=OC可知C点在O、B之间,可设C点表示的数为c,列方程得c-(-4)-(8-c)=c,解得c=4.
∴OC=4.
(3)①若P、Q同向运动,由题可知P、Q都沿数轴的负半轴方向运动,则t秒后P点对应的数为-4-2t,Q点对应的数为8-4t.
情况一:Q点没追上P点,则 (8-4t)-(-4-2t)=4,解得t=4.
情况二:Q点追上并超过P点,则(-4-2t)-(8-4t)=4,解得t=8.
②若P、Q相向运动,则t秒后P点对应的数为-4+2t,Q点对应的数为8-4t.
情况一:相遇前列方程得(8-4t)-(-4+2t)=4,解得.
情况二:相遇后列方程得(-4+2t)-(8-4t)=4,解得.
综上所述,若P、Q同向运动,则经过4秒或8秒后点P、Q两点相距4个单位长度;若P、Q相向运动,则经过或秒后点P、Q两点相距4个单位长度.
第1页,共1页
一、选择题:本题共10小题,每小题3分,共30分。在每小题给出的选项中,只有一项是符合题目要求的。
1.如果+50m表示向东走50m,那么向西走40m表示为( )
A. -50m B. -40m C. +40m D. +50m
2.若8xmy与6x3yn的和是单项式,则m+n的值为( )
A. 4 B. 8 C. -4 D. -8
3.根据文旅部的数据,2023年国庆假期前七天,国内出游人数达到7.54亿人次,旅游收入6630.9亿元.基本恢复甚至超越2019年同期统计,这是一个令人振奋的数据.其中数据6630.9亿用科学记数法表示为( )
A. 6.6309×108 B. 6.6309×109 C. 6.6309×1010 D. 6.6309×1011
4.如图是由若干个完全相同的小正方体组成的几何体,若从左面看这个几何体,则看到的平面图形是( )
A.
B.
C.
D.
5.式子a-(b-c+d)去括号的正确结果是( )
A. a+b+c+d B. a+b-c+d C. a-b-c+d D. a-b+c-d
6.在下列方程的变形中,正确的是( )
A. 由2x=-3得 B. 由得x=2
C. 由4x-3=3x得4x-3x=3 D. 由于得x=2
7.下列说法中,不正确的是( )
A. 零是绝对值最小的数 B. 倒数等于本身的数只有1
C. 相反数等于本身的数只有0 D. 原点左边的数离原点越远就越小
8.在数轴上表示a、b两数的点如图所示,则下列判断正确的是( )
A. ab>0 B. a+b>0 C. a+b<0 D. |a|>|b|
9.有一东西向的直线吊桥横跨溪谷,小维、阿良分别从西桥头、东桥头同时开始往吊桥的另一头笔直地走过去,如图所示,已知小维从西桥头走了84步,阿良从东桥头走了60步时,两人在吊桥上的某点交会,且交会之后阿良再走70步恰好走到西桥头,若小维每步的距离相等,阿良每步的距离相等,则交会之后小维再走多少步会恰好走到东桥头( )
A. 46 B. 50 C. 60 D. 72
10.点P在线段EF上,现有四个等式①PE=PF;②PE=EF;③EF=2PE;④2PE=EF;其中能表示点P是EF中点的有( )
A. 4个 B. 3个 C. 2个 D. 1个
二、填空题:本题共5小题,每小题3分,共15分。
11.方程2x=6的解是______.
12.某地某天的最高气温为3℃,最低气温为-8℃,这天的温差是______℃.
13.如图,C为线段AB上一点,D为线段BC的中点,AB=20,AD=14,则AC的长为______.
14.若m,n互为相反数,p,q互为倒数,则=______.
15.已知关于x的一元一次方程x+3=2x+b的解为x=2,那么关于y的一元一次方程(y+1)+3=2(y+1)+b的解为y= ______.
三、解答题:本题共9小题,共75分。解答应写出文字说明,证明过程或演算步骤。
16.(本小题8分)
计算:
(1)12-(-18)+(-7)-|-15|;
(2).
17.(本小题8分)
(1)列方程求解:把一些图书分给某班学生阅读,如果每人分3本,则剩余20本;如果每人分4本,则还缺25本.问这个班有多少学生?这些图书共有多少本?
(2)列方程求解:一个角的余角比这个角的补角的三分之一多6°,求这个角的大小.
18.(本小题8分)
解下列方程:
(1)3x+3=2x+7;
(2).
19.(本小题7分)
化简:
(1)x3-2x2-x3+5x2+4;
(2).
20.(本小题9分)
已知一个三角形的第一条边长为3a+b,第二条边比第一条边短a-2b,第三条边比第二条边长2a+b.
(1)则第二边的边长为______,第三条边的边长为______;
(2)用含a,b的式子表示这个三角形的周长,并化简;
(3)若a,b满足|a-8|+(b-7)2=0,求这个三角形的周长.
21.(本小题11分)
如图,点A在点O的北偏西60°的方向上,点B在点O的南偏东20°的方向上,OE平分∠AOB.求∠AOB和∠DOE的度数.
22.(本小题8分)
如图,已知A、B、C、D四点,请按下列要求画图:
(1)画直线AB;
(2)画射线BC;
(3)连接AC,在AC上求作点P使其到B、D两点的距离之和最小(注:不写作法,请保留作图痕迹).
理由是______.
23.(本小题8分)
以直线AB上一点O为端点作射线 OC,使∠BOC=60°,将一个直角三角形的直角顶点放在点O处.(注:∠DOE=90°)
(1)如图1,若直角三角板DOE的一边OD放在射线OB上,则∠COE=______°;
(2)如图2,将直角三角板DOE绕点O逆时针方向转动到某个位置,若OE恰好平分∠AOC,请说明OD所在射线是∠BOC的平分线;
(3)如图3,将三角板DOE绕点O逆时针转动到某个位置时,若恰好∠COD=∠AOE,求∠BOD的度数?
24.(本小题8分)
已知(a+4)x3-6xb-6+12x+5是关于x的二次三项式,在数轴上A、B两点所对应的数分别是a、b.
(1)a= ______,b= ______.
(2)若点C为数轴上一点,且CA-CB=OC,求OC的值;
(3)在数轴上,若点P以每秒2个单位的速度从A点出发,点Q以每秒4个单位的速度从B点出发,运动时间为t秒,经过几秒后,点P、Q两点相距4个单位长度?
1.【答案】B
2.【答案】A
3.【答案】D
4.【答案】D
5.【答案】D
6.【答案】C
7.【答案】B
8.【答案】C
9.【答案】D
10.【答案】B
11.【答案】x=3
12.【答案】11
13.【答案】8
14.【答案】
15.【答案】1
16.【答案】8;
55.
17.【答案】这个班有45名学生,图书有155本;
这个角是36°.
18.【答案】解:(1)3x+3=2x+7,
移项得:3x-2x=7-3,
合并同类项得:x=4;
(2),
去分母得:2(2x-1)-(10x+1)=3(2x+1)-12,
去括号得:4x-2-10x-1=6x+3-12,
移项,合并同类项得:-12x=-6,
未知数系数化为1得:.
19.【答案】3x2+4;
a2+a-2.
20.【答案】(1)2a+3b ;4a+4b;
(2)该三角形的周长为:(3a+b)+(2a+3b)+(4a+4b)
=3a+b+2a+3b+4a+4b
=9a+8b.
(3)由题意可知:a=8,b=7,
该三角形的周长为:9×8+8×7=128.
21.【答案】解:由题意得:∠AOC=90°-60°=30°,
∴∠AOB=30°+90°+20°=140°,
∵OE平分∠AOB,
∴,
∴∠DOE=∠EOB-∠DOB=50°,
∴∠AOB=140°,∠DOE=50°.
22.【答案】解:(1)如图,直线AB即为所作;
(2)如图,射线BC即为所作;
(3)如图,点P即为所求作的点.理由是:两点之间线段最短.
故答案为:两点之间线段最短.
23.【答案】解:(1)30;
(2)∵OE平分∠AOC,
∴∠COE=∠AOE=COA,
∵∠EOD=90°,
∴∠AOE+∠DOB=90°,∠COE+∠COD=90°,
∴∠COD=∠DOB,
∴OD所在射线是∠BOC的平分线;
(3)设∠COD=x°,则∠AOE=5x°,
∵∠DOE=90°,∠BOC=60°,
当OD边在∠AOC之间时,
6x=30,
解得x=5;
当OD边在∠BOC之间时,
5x+90-x=120,
解得x=7.5,
即∠COD=5°或7.5°,
∴∠BOD=∠COD+∠BOC=65°
或∠BOD=∠BOC-∠COD=52.5°.
24.【答案】(1)-4,8.
(2)由CA-CB=OC可知C点在O、B之间,可设C点表示的数为c,列方程得c-(-4)-(8-c)=c,解得c=4.
∴OC=4.
(3)①若P、Q同向运动,由题可知P、Q都沿数轴的负半轴方向运动,则t秒后P点对应的数为-4-2t,Q点对应的数为8-4t.
情况一:Q点没追上P点,则 (8-4t)-(-4-2t)=4,解得t=4.
情况二:Q点追上并超过P点,则(-4-2t)-(8-4t)=4,解得t=8.
②若P、Q相向运动,则t秒后P点对应的数为-4+2t,Q点对应的数为8-4t.
情况一:相遇前列方程得(8-4t)-(-4+2t)=4,解得.
情况二:相遇后列方程得(-4+2t)-(8-4t)=4,解得.
综上所述,若P、Q同向运动,则经过4秒或8秒后点P、Q两点相距4个单位长度;若P、Q相向运动,则经过或秒后点P、Q两点相距4个单位长度.
第1页,共1页
同课章节目录
