2024-2025学年北京市海淀区精诚教育海淀学部八年级(下)月考数学试卷(6月份)(含答案)
文档属性
| 名称 | 2024-2025学年北京市海淀区精诚教育海淀学部八年级(下)月考数学试卷(6月份)(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 158.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-24 19:16:21 | ||
图片预览




文档简介
2024-2025学年北京市海淀区精诚教育海淀学部八年级(下)月考数学试卷(6月份)
一、选择题:本题共8小题,每小题2分,共16分。在每小题给出的选项中,只有一项是符合题目要求的。
1.下列四组数中,能作为直角三角形三边长的是( )
A. 1, B. 1,,
C. 4,5,6 D. 3,4,6
2.二次根式中,字母a的取值范围是( )
A. a≥-3 B. a>-3 C. a>3 D. a≥3
3.如图,在 ABCD中,对角线AC、BD交于点O,下列式子中不一定成立的是( )
A. AB∥CD
B. OA=OC
C. ∠ABC+∠BCD=180°
D. AB=BC
4.在一次中学生田径运动会上,参加男子跳高的15名运动员的成绩如图所示,则这些运动员成绩的中位数为( )
A. 160 B. 165 C. 170 D. 175
5.如图,A,B,C三点在边长为1的正方形网格的格点上,则∠BAC的度数为( )
A. 30°
B. 45°
C. 50°
D. 60°
6.下列运算正确的是( )
A. += B. =2 C. ×= D. ÷=2
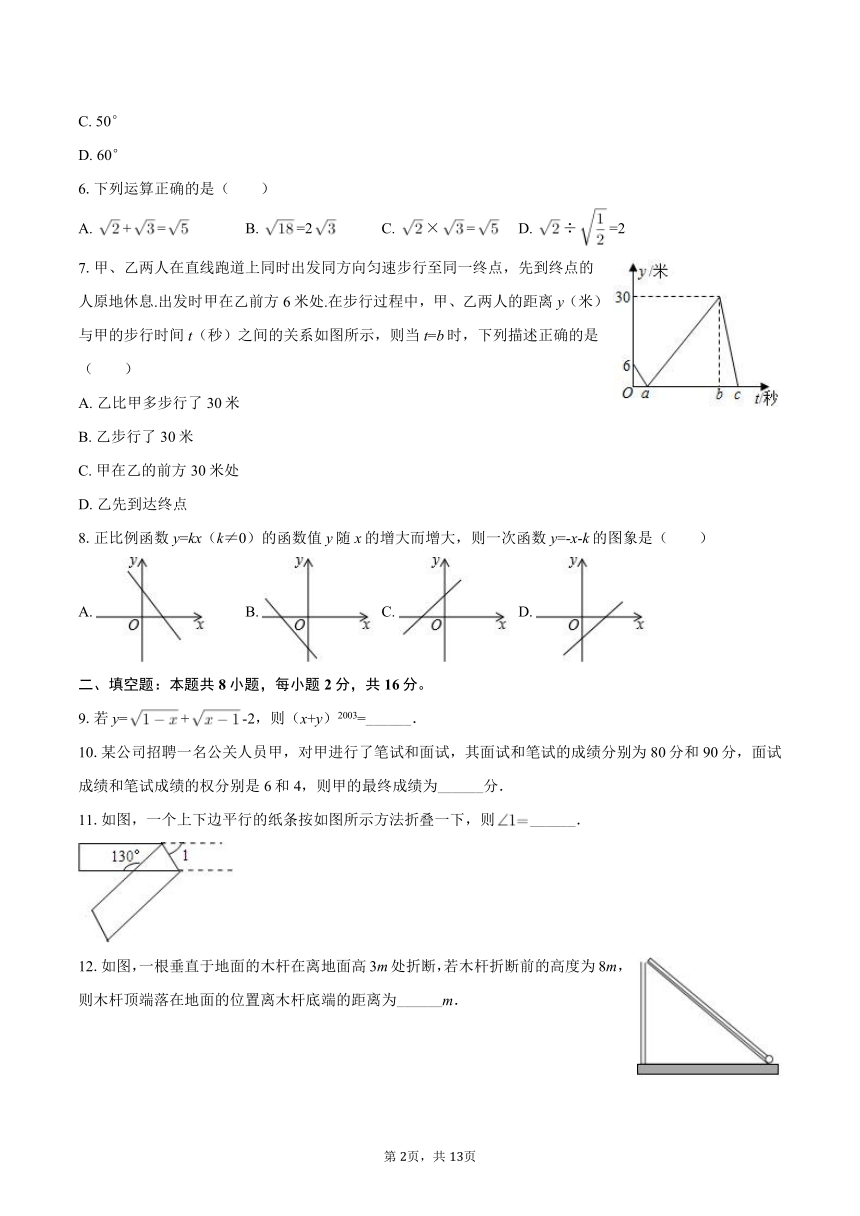
7.甲、乙两人在直线跑道上同时出发同方向匀速步行至同一终点,先到终点的人原地休息.出发时甲在乙前方6米处.在步行过程中,甲、乙两人的距离y(米)与甲的步行时间t(秒)之间的关系如图所示,则当t=b时,下列描述正确的是( )
A. 乙比甲多步行了30米
B. 乙步行了30米
C. 甲在乙的前方30米处
D. 乙先到达终点
8.正比例函数y=kx(k≠0)的函数值y随x的增大而增大,则一次函数y=-x-k的图象是( )
A. B. C. D.
二、填空题:本题共8小题,每小题2分,共16分。
9.若y=+-2,则(x+y)2003=______.
10.某公司招聘一名公关人员甲,对甲进行了笔试和面试,其面试和笔试的成绩分别为80分和90分,面试成绩和笔试成绩的权分别是6和4,则甲的最终成绩为______分.
11.如图,一个上下边平行的纸条按如图所示方法折叠一下,则______.
12.如图,一根垂直于地面的木杆在离地面高3m处折断,若木杆折断前的高度为8m,则木杆顶端落在地面的位置离木杆底端的距离为______m.
13.甲市到乙市的包裹邮资为每千克0.5元,每件另加手续费2元,则总邮资y(元)与包裹重量x(千克)之间的函数关系式是:______.
14.如图,在△ABC中,AB=3,AC=5,点D,E,F分别是AB,BC,AC的中点,则四边形ADEF的周长为______.
15.a和b互为相反数,并且它们的绝对值最小,则a=______,b=______.
16.如图,过矩形ABCD对角线的交点O,且分别交AB、CD于E、F,那么阴影部分的面积是矩形ABCD的面积的______.
三、解答题:本题共10小题,共68分。解答应写出文字说明,证明过程或演算步骤。
17.(本小题6分)
计算:.
18.(本小题6分)
如图,有一块土地形状如图所示,∠B=90°,AB=4米,BC=3米,CD=12米,AD=13米,请计算这块土地的面积.
19.(本小题6分)
如图,在线段AD上有两点E,F,且AE=DF,过点E,F分别作AD的垂线BE和CF,连接AB,CD,BF,CE,且AB∥CD.求证:四边形BECF是平行四边形.
20.(本小题7分)
已知:一次函数y=kx+b的图象经过点(-1,-5),且与正比例函数y=x的图象相交于点(2,a).求:
(1)求a的值;
(2)求一次函数的解析式.
21.(本小题7分)
某班在甲、乙两名同学中选拔一人参加学校数学竞赛,在相同的测试条件下,两人5次测试成绩(单位:分)如表:
次数 1 2 3 4 5
甲 79 86 82 85 83
乙 88 79 90 81 77
回答下列问题:
(1)请分别求出甲、乙两同学测试成绩的平均数;
(2)经计算知S2甲=6,S2乙=26.你认为选拔谁参加比赛更合适,说明理由.
22.(本小题7分)
暑假期间某中学校长决定带领市级“三好学生去北京旅游,甲旅行社承诺:“如果校长买全票一张,则学生可享受半价优惠”;乙旅行社承诺:“包括校长在内所有按全票的6折优惠”.若全票价为240元
(1)设学生数为x,甲、乙旅行社收费分别为y甲(元)和y乙(元),分别写出两个旅行社收费的表达式;
(2)当有学生20人时,哪家旅行社更优惠?
23.(本小题7分)
如图,在矩形ABCD中,对角线BD的垂直平分线MN与AD相交于点M,与BC相交于点N,连接BM,DN.
(1)求证:四边形BMDN是菱形;
(2)若AB=4,AD=8,求MD的长.
24.(本小题7分)
如图,在平面直角坐标系xOy中,直线y=-2x+a与y轴交于点C(0,6),与x轴交于点B.
(1)求这条直线的解析式;
(2)直线AD与(1)中所求的直线相交于点D(-1,n),点A的坐标为(-3,0).求n的值及直线AD的解析式.
25.(本小题7分)
近几年,昆明积极推进花卉景观大道建设,截至目前,主城区主干道已经陆续有100多条道路,形成了一定规模的花卉景观效果,展现了“春城无处不飞花”的城市景观.环湖路沿线准备种植甲、乙两种花卉,经市场调查,甲种花并的种植费用y(元)与种植面积x(m2)之间的函数关系如图所示,乙种花卉的种植费用为每平方米80元.
(1)请求出甲种花卉y与x之间的函数关系式;
(2)已知甲、乙两种花卉的种植面积共6000m2,甲种花卉的种植面积不少于3000m2.若甲种花卉种植面积不超过乙种花卉种植面积的2倍,设种植总费用为w元,求出w与甲种花卉种植面积x之间的函数关系式及w的最小值.
26.(本小题8分)
在平面直角坐标系xOy中,已知点M不与原点重合.对于点P给出如下定义:点P关于点M的对称点为P′,点P′关于直线OM的对称点为Q,称点Q是点P关于点M的“转称点”.
(1)如图,已知点M(t,0),P(t+1,1),点Q是点P关于点M的“转称点”.
①当t=2时,在图中画出点Q的位置,并直接写出点Q的坐标;
②PQ的长度是否与t有关?若无关,求PQ的长;若有关,说明理由;
(2)已知点A(3,4),△ABC是边长为2的等边三角形(点A,B,C按逆时针方向排列),点N是点B关于点C的“转称点”,在△ABC绕点A旋转的过程中,当BN最大时,直接写出此时OB的长.
1.【答案】A
2.【答案】A
3.【答案】D
4.【答案】B
5.【答案】B
6.【答案】D
7.【答案】D
8.【答案】B
9.【答案】-1
10.【答案】84
11.【答案】65°
12.【答案】4
13.【答案】y=0.5x+2
14.【答案】8
15.【答案】0 0
16.【答案】
17.【答案】.
18.【答案】解:∵∠B=90°,AB=4米,BC=3米,
∴AC===5(米).
∵△ACD中,AC=5米,CD=12米,AD=13米,52+122=132,即AC2+CD2=AD2,
∴△ACD是直角三角形,
∴S=S△ABC+S△ACD=AB BC+AC CD=×4×3+×5×12=36(平方米).
19.【答案】证明:∵BE⊥AD,CF⊥AD,
∴∠AEB=∠BEF=∠CFE=∠CFD=90°,
∴BE∥CF,
∵AB∥CD,
∴∠A=∠D,
在△AEB和△DFC中,
,
∴△AEB≌△DFC(ASA),
∴BE=CF,
∵BE∥CF,
∴四边形BECF是平行四边形.
20.【答案】解:(1)把点(2,a)代入正比例函数的解析式y=x得a=×2=1,
即a的值为1;
(2)把点(-1,-5)、(2,1)代入y=kx+b,
得,
解得,
所以一次函数的解析式为y=2x-3.
21.【答案】解:(1)甲的平均分为:(79+86+82+85+83)=83(分),
乙的平均分为:(88+79+90+81+77)=83(分);
(2)选拔甲参加比赛更合适,理由如下:
因为甲、乙两人的平均分相同,说明两人水平差不多,而S甲2<S乙2,说明甲比乙发挥稳定,所以选拔甲参加比赛更合适.
22.【答案】解:(1)y甲=240+120x;
y乙=240×60%(x+1);
(2)分三种情况讨论:即两家都一样;甲更优惠;乙更优惠.
240+120x=240×60%(x+1)
解得x=4,
当x>4时,y乙>y甲,
当x<4时,y乙<y甲
所以当有4名学生时,两家同样;
当大于4名时,甲比较划算;
当小于4名时,乙比较划算.
∴当有学生20人时,甲旅行社更优惠.
23.【答案】解:(1)证明:∵四边形ABCD是矩形,
∴AD∥BC,∠A=90°,
∴∠MDO=∠NBO,∠DMO=∠BNO,
∵在△DMO和△BNO中,
,
∴△DMO≌△BNO(AAS),
∴OM=ON,
∵OB=OD,
∴四边形BMDN是平行四边形,
∵MN⊥BD,
∴平行四边形BMDN是菱形.
(2)解:∵四边形BMDN是菱形,
∴MB=MD,
设MD长为x,则MB=DM=x,
在Rt△AMB中,BM2=AM2+AB2
即x2=(8-x)2+42,
解得:x=5,
所以MD长为5.
24.【答案】解:(1)直线y=-2x+a与y轴交于点C(0,6),
∴-2×0+a=6,
∴a=6,
∴直线的解析式为y=-2x+6;
(2)点D(-1,n)在y=-2x+6上,
∴n=-2×(-1)+6=8,
∴D(-1,8),
设直线AD的解析式为y=kx+b,
把点A(-3,0)和D(-1,8)代入得,
解得,
∴直线AD的解析式为y=4x+12.
25.【答案】解:(1)当0≤x<300时,
设y=mx(m≠0),则300m=39000,
解得,m=130,
∴y=130x(0≤x<300),
当x≥300时,设y=kx+b(k≠0),
则,
解得,
此时,y=100x+9000,(x≥300),
∴综上所述,.
(2)由题意,甲种花卉种植x m2(x≥3000),则乙种花卉种植(6000-x)m2,
∵x≥3000,
∴w=100x+9000+80(6000-x)
=20x+489000,
又∵x≤2(6000-x),
则x≤4000,
∴3000≤x≤4000.
∵w=20x+489000中,k=20>0,w随x的增大而增大,
∴当x=3000时,w最小,
w最小=20×3000+489000=549000(元).
26.【答案】解:(1)①当t=2时,点M(2,0),P(3,1),
如图:
∵点Q是点P关于点M的“转称点”.
∴P′(1,-1),Q(1,1);
②∵点M(t,0),P(t+1,1),
∴P′(t-1,-1),Q(t-1,1),
∴PQ∥x轴,
∴PQ=t+1-(t-1)=2;
∴PQ的长度与t有无关,PQ的长为2;
(2)如图:
由“转称点”的定义得C为BB′的中点,D为NB′的中点,
∴CD∥BN,CD=BN,
∴当CD最大时,BN最大,
由图得在△ABC绕点A旋转的过程中,当O、B,C、B′共线时,BN最大,
如图1:
∵△ABC是边长为2的等边三角形
∴BC=CB′=2,AH=,BH=1,
∵点A(3,4),
∴OA==5,
∴OH===,
∴OB=-1.
如图2:
∵△ABC是边长为2的等边三角形
∴BC=CB′=2,AH=,BH=1,
∵点A(3,4),
∴OA==5,
∴OH===,
∴OB=OH+BH=+1.
综上,当BN最大时,OB的长为+1或-1.
第1页,共1页
一、选择题:本题共8小题,每小题2分,共16分。在每小题给出的选项中,只有一项是符合题目要求的。
1.下列四组数中,能作为直角三角形三边长的是( )
A. 1, B. 1,,
C. 4,5,6 D. 3,4,6
2.二次根式中,字母a的取值范围是( )
A. a≥-3 B. a>-3 C. a>3 D. a≥3
3.如图,在 ABCD中,对角线AC、BD交于点O,下列式子中不一定成立的是( )
A. AB∥CD
B. OA=OC
C. ∠ABC+∠BCD=180°
D. AB=BC
4.在一次中学生田径运动会上,参加男子跳高的15名运动员的成绩如图所示,则这些运动员成绩的中位数为( )
A. 160 B. 165 C. 170 D. 175
5.如图,A,B,C三点在边长为1的正方形网格的格点上,则∠BAC的度数为( )
A. 30°
B. 45°
C. 50°
D. 60°
6.下列运算正确的是( )
A. += B. =2 C. ×= D. ÷=2
7.甲、乙两人在直线跑道上同时出发同方向匀速步行至同一终点,先到终点的人原地休息.出发时甲在乙前方6米处.在步行过程中,甲、乙两人的距离y(米)与甲的步行时间t(秒)之间的关系如图所示,则当t=b时,下列描述正确的是( )
A. 乙比甲多步行了30米
B. 乙步行了30米
C. 甲在乙的前方30米处
D. 乙先到达终点
8.正比例函数y=kx(k≠0)的函数值y随x的增大而增大,则一次函数y=-x-k的图象是( )
A. B. C. D.
二、填空题:本题共8小题,每小题2分,共16分。
9.若y=+-2,则(x+y)2003=______.
10.某公司招聘一名公关人员甲,对甲进行了笔试和面试,其面试和笔试的成绩分别为80分和90分,面试成绩和笔试成绩的权分别是6和4,则甲的最终成绩为______分.
11.如图,一个上下边平行的纸条按如图所示方法折叠一下,则______.
12.如图,一根垂直于地面的木杆在离地面高3m处折断,若木杆折断前的高度为8m,则木杆顶端落在地面的位置离木杆底端的距离为______m.
13.甲市到乙市的包裹邮资为每千克0.5元,每件另加手续费2元,则总邮资y(元)与包裹重量x(千克)之间的函数关系式是:______.
14.如图,在△ABC中,AB=3,AC=5,点D,E,F分别是AB,BC,AC的中点,则四边形ADEF的周长为______.
15.a和b互为相反数,并且它们的绝对值最小,则a=______,b=______.
16.如图,过矩形ABCD对角线的交点O,且分别交AB、CD于E、F,那么阴影部分的面积是矩形ABCD的面积的______.
三、解答题:本题共10小题,共68分。解答应写出文字说明,证明过程或演算步骤。
17.(本小题6分)
计算:.
18.(本小题6分)
如图,有一块土地形状如图所示,∠B=90°,AB=4米,BC=3米,CD=12米,AD=13米,请计算这块土地的面积.
19.(本小题6分)
如图,在线段AD上有两点E,F,且AE=DF,过点E,F分别作AD的垂线BE和CF,连接AB,CD,BF,CE,且AB∥CD.求证:四边形BECF是平行四边形.
20.(本小题7分)
已知:一次函数y=kx+b的图象经过点(-1,-5),且与正比例函数y=x的图象相交于点(2,a).求:
(1)求a的值;
(2)求一次函数的解析式.
21.(本小题7分)
某班在甲、乙两名同学中选拔一人参加学校数学竞赛,在相同的测试条件下,两人5次测试成绩(单位:分)如表:
次数 1 2 3 4 5
甲 79 86 82 85 83
乙 88 79 90 81 77
回答下列问题:
(1)请分别求出甲、乙两同学测试成绩的平均数;
(2)经计算知S2甲=6,S2乙=26.你认为选拔谁参加比赛更合适,说明理由.
22.(本小题7分)
暑假期间某中学校长决定带领市级“三好学生去北京旅游,甲旅行社承诺:“如果校长买全票一张,则学生可享受半价优惠”;乙旅行社承诺:“包括校长在内所有按全票的6折优惠”.若全票价为240元
(1)设学生数为x,甲、乙旅行社收费分别为y甲(元)和y乙(元),分别写出两个旅行社收费的表达式;
(2)当有学生20人时,哪家旅行社更优惠?
23.(本小题7分)
如图,在矩形ABCD中,对角线BD的垂直平分线MN与AD相交于点M,与BC相交于点N,连接BM,DN.
(1)求证:四边形BMDN是菱形;
(2)若AB=4,AD=8,求MD的长.
24.(本小题7分)
如图,在平面直角坐标系xOy中,直线y=-2x+a与y轴交于点C(0,6),与x轴交于点B.
(1)求这条直线的解析式;
(2)直线AD与(1)中所求的直线相交于点D(-1,n),点A的坐标为(-3,0).求n的值及直线AD的解析式.
25.(本小题7分)
近几年,昆明积极推进花卉景观大道建设,截至目前,主城区主干道已经陆续有100多条道路,形成了一定规模的花卉景观效果,展现了“春城无处不飞花”的城市景观.环湖路沿线准备种植甲、乙两种花卉,经市场调查,甲种花并的种植费用y(元)与种植面积x(m2)之间的函数关系如图所示,乙种花卉的种植费用为每平方米80元.
(1)请求出甲种花卉y与x之间的函数关系式;
(2)已知甲、乙两种花卉的种植面积共6000m2,甲种花卉的种植面积不少于3000m2.若甲种花卉种植面积不超过乙种花卉种植面积的2倍,设种植总费用为w元,求出w与甲种花卉种植面积x之间的函数关系式及w的最小值.
26.(本小题8分)
在平面直角坐标系xOy中,已知点M不与原点重合.对于点P给出如下定义:点P关于点M的对称点为P′,点P′关于直线OM的对称点为Q,称点Q是点P关于点M的“转称点”.
(1)如图,已知点M(t,0),P(t+1,1),点Q是点P关于点M的“转称点”.
①当t=2时,在图中画出点Q的位置,并直接写出点Q的坐标;
②PQ的长度是否与t有关?若无关,求PQ的长;若有关,说明理由;
(2)已知点A(3,4),△ABC是边长为2的等边三角形(点A,B,C按逆时针方向排列),点N是点B关于点C的“转称点”,在△ABC绕点A旋转的过程中,当BN最大时,直接写出此时OB的长.
1.【答案】A
2.【答案】A
3.【答案】D
4.【答案】B
5.【答案】B
6.【答案】D
7.【答案】D
8.【答案】B
9.【答案】-1
10.【答案】84
11.【答案】65°
12.【答案】4
13.【答案】y=0.5x+2
14.【答案】8
15.【答案】0 0
16.【答案】
17.【答案】.
18.【答案】解:∵∠B=90°,AB=4米,BC=3米,
∴AC===5(米).
∵△ACD中,AC=5米,CD=12米,AD=13米,52+122=132,即AC2+CD2=AD2,
∴△ACD是直角三角形,
∴S=S△ABC+S△ACD=AB BC+AC CD=×4×3+×5×12=36(平方米).
19.【答案】证明:∵BE⊥AD,CF⊥AD,
∴∠AEB=∠BEF=∠CFE=∠CFD=90°,
∴BE∥CF,
∵AB∥CD,
∴∠A=∠D,
在△AEB和△DFC中,
,
∴△AEB≌△DFC(ASA),
∴BE=CF,
∵BE∥CF,
∴四边形BECF是平行四边形.
20.【答案】解:(1)把点(2,a)代入正比例函数的解析式y=x得a=×2=1,
即a的值为1;
(2)把点(-1,-5)、(2,1)代入y=kx+b,
得,
解得,
所以一次函数的解析式为y=2x-3.
21.【答案】解:(1)甲的平均分为:(79+86+82+85+83)=83(分),
乙的平均分为:(88+79+90+81+77)=83(分);
(2)选拔甲参加比赛更合适,理由如下:
因为甲、乙两人的平均分相同,说明两人水平差不多,而S甲2<S乙2,说明甲比乙发挥稳定,所以选拔甲参加比赛更合适.
22.【答案】解:(1)y甲=240+120x;
y乙=240×60%(x+1);
(2)分三种情况讨论:即两家都一样;甲更优惠;乙更优惠.
240+120x=240×60%(x+1)
解得x=4,
当x>4时,y乙>y甲,
当x<4时,y乙<y甲
所以当有4名学生时,两家同样;
当大于4名时,甲比较划算;
当小于4名时,乙比较划算.
∴当有学生20人时,甲旅行社更优惠.
23.【答案】解:(1)证明:∵四边形ABCD是矩形,
∴AD∥BC,∠A=90°,
∴∠MDO=∠NBO,∠DMO=∠BNO,
∵在△DMO和△BNO中,
,
∴△DMO≌△BNO(AAS),
∴OM=ON,
∵OB=OD,
∴四边形BMDN是平行四边形,
∵MN⊥BD,
∴平行四边形BMDN是菱形.
(2)解:∵四边形BMDN是菱形,
∴MB=MD,
设MD长为x,则MB=DM=x,
在Rt△AMB中,BM2=AM2+AB2
即x2=(8-x)2+42,
解得:x=5,
所以MD长为5.
24.【答案】解:(1)直线y=-2x+a与y轴交于点C(0,6),
∴-2×0+a=6,
∴a=6,
∴直线的解析式为y=-2x+6;
(2)点D(-1,n)在y=-2x+6上,
∴n=-2×(-1)+6=8,
∴D(-1,8),
设直线AD的解析式为y=kx+b,
把点A(-3,0)和D(-1,8)代入得,
解得,
∴直线AD的解析式为y=4x+12.
25.【答案】解:(1)当0≤x<300时,
设y=mx(m≠0),则300m=39000,
解得,m=130,
∴y=130x(0≤x<300),
当x≥300时,设y=kx+b(k≠0),
则,
解得,
此时,y=100x+9000,(x≥300),
∴综上所述,.
(2)由题意,甲种花卉种植x m2(x≥3000),则乙种花卉种植(6000-x)m2,
∵x≥3000,
∴w=100x+9000+80(6000-x)
=20x+489000,
又∵x≤2(6000-x),
则x≤4000,
∴3000≤x≤4000.
∵w=20x+489000中,k=20>0,w随x的增大而增大,
∴当x=3000时,w最小,
w最小=20×3000+489000=549000(元).
26.【答案】解:(1)①当t=2时,点M(2,0),P(3,1),
如图:
∵点Q是点P关于点M的“转称点”.
∴P′(1,-1),Q(1,1);
②∵点M(t,0),P(t+1,1),
∴P′(t-1,-1),Q(t-1,1),
∴PQ∥x轴,
∴PQ=t+1-(t-1)=2;
∴PQ的长度与t有无关,PQ的长为2;
(2)如图:
由“转称点”的定义得C为BB′的中点,D为NB′的中点,
∴CD∥BN,CD=BN,
∴当CD最大时,BN最大,
由图得在△ABC绕点A旋转的过程中,当O、B,C、B′共线时,BN最大,
如图1:
∵△ABC是边长为2的等边三角形
∴BC=CB′=2,AH=,BH=1,
∵点A(3,4),
∴OA==5,
∴OH===,
∴OB=-1.
如图2:
∵△ABC是边长为2的等边三角形
∴BC=CB′=2,AH=,BH=1,
∵点A(3,4),
∴OA==5,
∴OH===,
∴OB=OH+BH=+1.
综上,当BN最大时,OB的长为+1或-1.
第1页,共1页
同课章节目录
