河南省天立教育2026届九年级上学期开学考试数学试卷(含答案)
文档属性
| 名称 | 河南省天立教育2026届九年级上学期开学考试数学试卷(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 999.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-26 12:08:31 | ||
图片预览



文档简介
河南省河南省天立教育2025-2026学年九年级上学期开学数学试题
一、单选题
1.已知一次函数的图象如图,则下列说法正确的是( )
A. B.当时,
C.函数值y随自变量x的增大而减小 D.图象与y轴交于点
2.数学课上,老师在黑板上画出了菱形,并以点为圆心,的长为半径画弧,交直线于点,连接,关于四边形的形状,让同学们进行讨论,小明认为:只有当时,四边形是菱形;小红认为:当时,四边形是正方形,小刚认为:四边形是菱形,且,与的度数无关,下列判断正确的是( )
A.小明和小红正确,小刚错误 B.小红和小刚正确,小明错误
C.小明和小刚错误,小红正确 D.小明和小红错误,小刚正确
3.已知菱形的周长为,两条对角线的和为6,则菱形的面积为( )
A.2 B. C.3 D.4
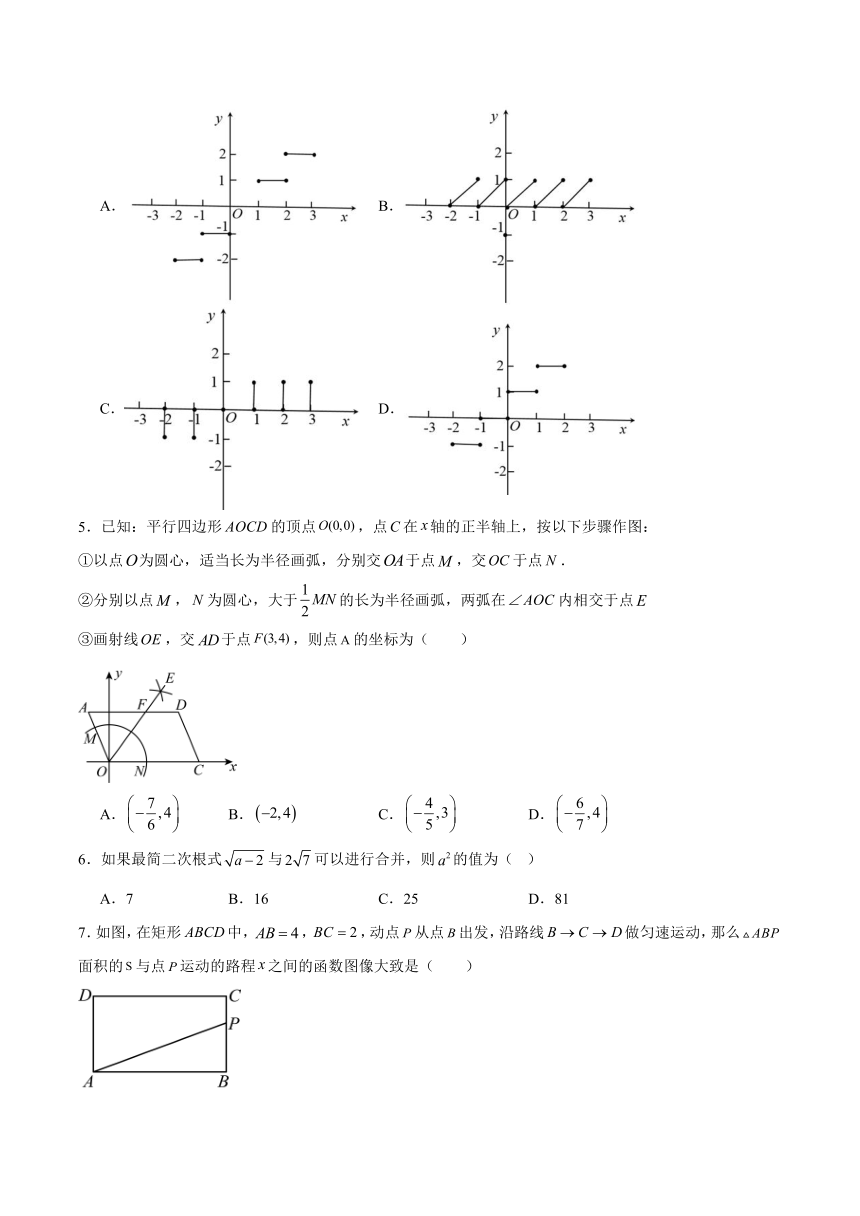
4.规定表示不大于的最大整数,例如,,.那么函数的图象为( )
A. B.
C. D.
5.已知:平行四边形的顶点,点在轴的正半轴上,按以下步骤作图:
①以点为圆心,适当长为半径画弧,分别交于点,交于点.
②分别以点,为圆心,大于的长为半径画弧,两弧在内相交于点
③画射线,交于点,则点的坐标为( )
A. B. C. D.
6.如果最简二次根式与可以进行合并,则的值为( )
A.7 B.16 C.25 D.81
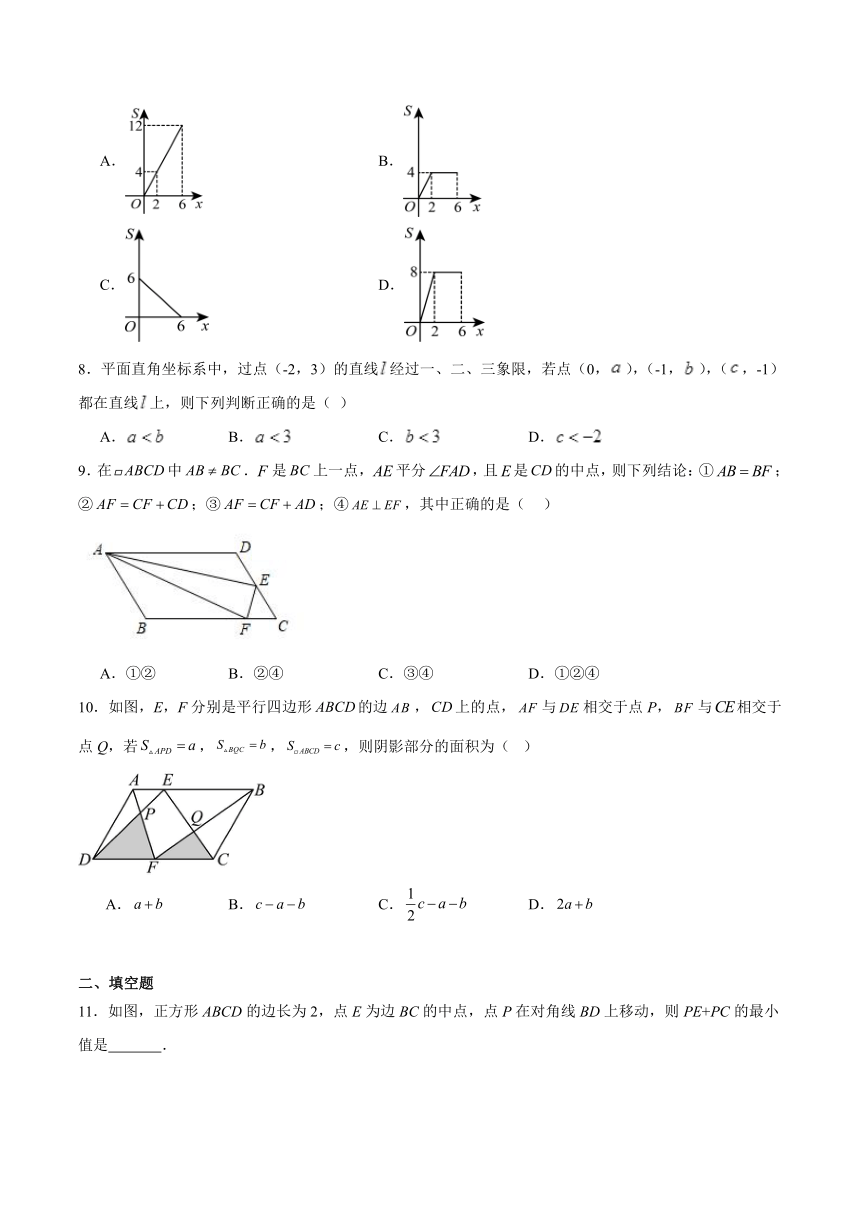
7.如图,在矩形中,,,动点从点出发,沿路线做匀速运动,那么面积的与点运动的路程之间的函数图像大致是( )
A. B.
C. D.
8.平面直角坐标系中,过点(-2,3)的直线经过一、二、三象限,若点(0,),(-1,),(,-1)都在直线上,则下列判断正确的是( )
A. B. C. D.
9.在中.是上一点,平分,且是的中点,则下列结论:①;②;③;④,其中正确的是( )
A.①② B.②④ C.③④ D.①②④
10.如图,E,F分别是平行四边形的边,上的点,与相交于点P,与相交于点Q,若,,,则阴影部分的面积为( )
A. B. C. D.
二、填空题
11.如图,正方形ABCD的边长为2,点E为边BC的中点,点P在对角线BD上移动,则PE+PC的最小值是 .
12.若最简二次根式与是同类二次根式,则x的值为 .
13.在四边形中,,给出下列4组条件:①,②,③,④.其中,不能得到“四边形是平行四边形”的条件是 .(只填序号)
14.为了响应学校“书香校园”建设,阳光班的同学们积极捐书,其中宏志学习小组的6名同学捐书册数分别是:5,7,x,8,4,6.已知他们平均每人捐6本,则这组数据的中位数是 .
15.矩形中,,是的中点,点在直线上,且,若与关于直线对称,则的长为 .
三、解答题
16.一条笔直的公路上依次有A、B、C三地,甲车从A地驶往C地,乙车从A地驶往B地,修好后立即以原速的两倍继续前进到达B地;如图是甲、乙两车与A地的距离y(千米)(小时)之间的大致图象.
(1)求B、C两地之间的距离;
(2)什么时候乙追上甲;
(3)当两车相距40千米时,甲车行驶了多长时间.
17.如图,在中,,,E,F分别为,的中点,过点B作的平行线与的延长线交于点D,连接,.
(1)求证:四边形为菱形;
(2)若,求四边形的面积.
18.小明对菱形的作法非常感兴趣,他根据所学的知识,利用直尺和圆规,在内分别以,为圆心,以的长为半径画弧,分别交,于点,,快速地作出一个菱形,如图()所示,根据小明的尺规作图过程,解决下列问题.
(1)小明用到的作图依据是( )
.一组对边平行且相等的四边形是菱形
.两组对边分别相等的四边形是菱形
.有一组邻边相等的平行四边形是菱形
.对角线互相垂直的平行四边形是菱形
(2)请在图()内运用另一种尺规作图的方法作出菱形,并证明你的结论.(保留作图痕迹,不写作法)
19.如图,在平行四边形ABCD中,AE平分∠DAB,已知CE=6,BE=8,DE=10.
(1)求BC的长;
(2)若∠CBE=36°,求∠ADC.
20.某学校计划组织452人参加社会实践活动,与某汽车租赁公司接洽后,得知该公司有型和型两种客车,它们的载客量和租金如下表所示.
A型客车 B型客车
载客量/(人辆) 45 26
租金/(元/辆) 400 240
经测算,租用型和型客车共13辆较为合理.设租用型客车辆.
(1)用含的代数式填写下表.
车量数/辆 载客量/人 租金/元
A型客车
B型客车
(2)采用怎样的租车方案可以使总的租车费用最低?最低为多少?
21.如图,在四边形ABCD中,AD∥BC,∠B=∠C,求证:AB=CD.
22.已知,如图,在平行四边形ABCD中,E、F分别为边AB、CD的中点,对角线的中点,对角线BD平分.
(1)求证:四边形BEDF为菱形;
(2)若AG//DB交CB的延长线于G,求证:四边形AGBD为矩形.
23.皇家驿站今年五一期间吸引了各地的游客前来观光,驻马店特产“伏陈醋”和“小磨香油”等也大受欢迎.某经销商抓住商机,计划购进某种包装的“伏陈醋”和“小磨香油”共100瓶,已知购进10瓶“伏陈醋”和20瓶“小磨香油”共需620元,购进30瓶“伏陈醋”和40瓶“小磨香油”共需1360元.
(1)每瓶“伏陈醋”和“小磨香油”的进价分别是多少元?
(2)结合游客的实际需求,该经销商决定购进“伏陈醋”的数量不超过“小磨香油”数量的,请你帮他计算如何进货才能使所花费用最少,最少费用是多少元?
参考答案
1.D
解:根据一次函数图像可知:函数值y随自变量x的增大而增大,,即A、C选项错误;由于k的值不确定,则一次函数与x轴交点坐标不确定,故B选项错误;当时,,即图象与y轴交于点,则D选项正确,符合题意.
故选:D.
2.D
解:∵菱形,
∴,,,
∴,,
由作图可得:,
∴,
∴四边形为菱形;为等边三角形,
∴,
∴,
∴小明认为:只有当时,四边形是菱形;说法错误;
小刚认为:四边形是菱形,且,与的度数无关,说法正确;
当时,而,
∴四边形不是正方形,
小红认为:当时,四边形是正方形,说法错误;
故选D
3.D
解:如图
四边形ABCD是菱形,AC+BD=6,菱形的周长为,
∴AB=,AC⊥BD,AO=AC,BO=BD,
∴AO+BO=3,
∴AO2+BO2=AB2,(AO+BO)2=9,
即AO2+BO2=5,AO2+2AO BO+BO2=9,
∴2AO BO=4,
∴菱形的面积=AC BD=2AO BO=4;
故选:D.
4.A
解:由已知得:当0≤x<1时,y=[x]=0,
当1≤x<2时,y=[x]=1,
当2≤x<3时,y=[x]=2,
当-1≤x<0时,y=[x]=-1,
当-2≤x<-1时,y=[x]=-2,
……
由以上可得A选项符合题意,
故选:A.
5.A
解:交轴于点,如图,
由作法得平分,
,
四边形为平行四边形,
∴,
,
,
设,则,
,
,,
,
,
在中,,
解得,
点坐标为.
故选:A.
6.D
解:最简二次根式与可以合并,
,
解得:,
∴
故选:D.
7.B
解:当点在线段上运动时,
∵,线段的长度将随着点沿路线运动的过程中而增大,
∴的面积随点的增大而增大,
当点与点重合时,
∵,,
∴,
当点在线段上运动时,的底边,边上的高的长是,
∴,
即此时的面积为定值,不随点的变化而变化,
∴符合题意的是B选项所表示的图像.
故选:B.
8.D
解:根据直线l经过第一、二、三象限且过点(-2,3),所以y随x的增大而增大.
因为-2<-1<0,所以3又因点(c,-1)在直线l上,所以c<-2.
故选D.
9.C
解:延长AD,交FE的延长线于点M,
∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠M=∠EFC,
∵E是CD的中点,
∴DE=CE,
在△DEM和△CEF中,
,
∴△DEM≌△CEF(AAS),
∴EM=EF,
∵AE平分∠FAD,
∴AM=AF,AE⊥EF.
即AF=AD+DM=CF+AD;故③,④正确,②错误.
∵AF不一定是∠BAD的角平分线,
∴AB不一定等于BF,故①错误.
故选:C.
10.C
解:连接、两点,过点作于点,
∵,,
∴,
∵四边形是平行四边形,
∴,
∴的边上的高与的边上的高相等,的边上的高与的边上的高相等,
∴,,
∴,即,
,即,
∵,,
∴,,
∴,
∴阴影部分的面积.
故选:C.
11.
解:如图,连接AE,
∵点C关于BD的对称点为点A,
∴PE+PC=PE+AP,
根据两点之间线段最短可得AE就是AP+PE的最小值,
∵正方形ABCD的边长为2,E是BC边的中点,
∴BE=1,
∴AE=.
故答案为:.
12.2.
∵最简二次根式与是同类二次根式,
∴x2﹣2=2x﹣2,
解得:x1=0,x2=2,
当x=0时与是无意义,
所以x=0舍去,
故答案为:2.
13.②
①,则一组对边平行且相等,可得到四边形是平行四边形,不符合题意;
②,无法得到四边形是平行四边形,符合题意;
③,两组对边分别平行,可得到四边形是平行四边形,不符合题意;
④,则此两角都是的补角,而与为同旁内角互补,可推出,两组对边分别平行,可得到四边形是平行四边形,不符合题意;
故答案为:②
14.6
由题意可得:=6,可知:x=6,将该数据从小到大排列得:4,5,6,6,7,8,故中位数为=6,故答案为6.
15.或
解:如图①,
与关于直线对称,
,
四边形是矩形,
,
,
;
如图②,
与关于直线对称,
,
四边形是矩形,
,
,
,
,
,
则的长为或.
故答案为:或.
16.(1)60千米
(2)出发后4.5小时
(3)或3.5或小时
(1)乙前面的速度为:(千米/小时),
乙后来的速度为:(千米/小时),
(千米),
答:B、C两地之间的距离为60千米;
(2)甲的速度为:(千米/小时),
设乙t小时追上甲,
根据题意得,
解得,
答:出发后4.5小时乙追上甲;
(3)当时,两车距离小于40,
①当时,
设甲距离A地的距离y(千米)与出发时间x(小时)之间的关系式为,
代入可得,
,
,解得;
②当时,
由(1)可得,A、B两地之间的距离为:,
设乙与A地距离与出发时间x之间的函数关系式为,
代入和
得,
解得,
,
解方程得(不合题意,舍去),
解方程得;
③当时,
解方程得.
答:当两车相距40千米时,甲车行驶了或3.5或小时.
17.(1)见解析;
(2)四边形的面积为.
(1)证明:∵,
∴,
∵为中点,
∴,
在和中
∴(ASA),
∴,
∵,
∴四边形是平行四边形,
∵为中点,为中点,
∴,
∵,
∴,
即,
∴四边形为菱形;
(2)解:∵,E,F分别为,的中点,
∴,,
∵,
∴,
∴,
在中,由勾股定理得:,
解得:,
∵,,
∴,,
∴四边形的面积为:
.
即:四边形的面积为.
18.(1)C;
(2)作图、证明见解析.
(1)解:根据作图,,
∵四边形是平行四边形,
∴,即,
∵,
∴四边形是平行四边形,
∵,
∴平行四边形是菱形,
用到的作图依据有一组对边平行且相等的四边形是平行四边形,有一组邻边相等的平行四边形是萎形,
故选:C;
(2)解:连接,作的中垂线交于,则四边形是菱形,
理由:由作图可知:,,,
∵四边形是平行四边形,
∴,
∴,
∵,,
∴,
∴,
∴四边形是平行四边形,
∵,
∴四边形是菱形
19.(1)BC=10;(2)126°.
解:(1)∵四边形ABCD是平行四边形,
∴AD=BC,DC∥AB,
∴∠DEA=∠EAB,
∵AE平分∠DAB,
∴∠DAE=∠EAB,
∴∠DAE=∠DEA,
∴AD=DE=10,
∴BC=10;
(2)∵CE=6,BE=8,BC=10,
∴CE2+BE2=62+82=100=BC2,
∴△BCE是直角三角形,且∠BEC=90°,
∴∠C=90°﹣∠CBE=90°﹣36°=54°,
∵AD∥BC,
∴∠D=180°﹣∠C=180°﹣54°=126°.
20.(1);
(2)租型车6辆、型车7辆时,总的租车费用最低,最低为4080元
(1)解:设租用型客车辆,则租用型客车辆,
型车的载客量,租金为.
故答案为:;.
(2)设租车的总费用为元,则有:.
由已知得:,
解得:.
在中,
当时,取最小值,最小值为4080元.
故租型车6辆、型车7辆时,总的租车费用最低,最低为4080元.
21.见解析
过点D作DF∥AB,
∵AD∥BC,
∴四边形ABFD是平行四边形,
∴AB=DF,∠DFC=∠B,
∵∠B=∠C,
∴∠DFC=∠C,
∴DF=DC,
∴AB=CD.
22.(1)见解析
(2)见解析
(1)证明:∵四边形ABCD是平行四边形,
∴AD=BC,ABCD,
∵E、F分别为边AB、CD的中点,
∴DF=EB,DFEB,
∴四边形DEBF是平行四边形,
∵DB平分∠EDF,
∴∠EDB=∠FDB,
∵DFEB,
∴∠FDB=∠EBD,
∴DE=BE,
又∵四边形DEBF是平行四边形,
∴四边形DEBF是菱形.
(2)证明:连接EF交BD于点O,
∵四边形DEBF是菱形,
∴EF⊥DB,OD=OB,
又∵E为AB的中点,
∴OEAD,
∴AD⊥BD,
∴∠ADB=90°,
∵ADBG,AGBD,
∴四边形AGBD为平行四边形,
∵∠ADB=90°,
∴四边形AGBD为矩形.
23.(1)每瓶“伏陈醋”的进价是12元,每瓶“小磨香油”的进价是25元
(2)购进“伏陈醋”40瓶,“小磨香油”60瓶,才能使所花费用最少,最少费用是1980元
(1)设每瓶“伏陈醋”的进价是元,每瓶“小磨香油”的进价是元,
根据题意得:,
解得,
每瓶“伏陈醋”的进价是12元,每瓶“小磨香油”的进价是25元;
(2)设购进“伏陈醋” 瓶,则购进“小磨香油” 瓶,
购进“伏陈醋”的数量不超过“小磨香油”数量的,
,
解得:,
设他所花费用为元,
根据题意得,
,
随增大而减小,
当时,取最小值(元,
此时,
购进“伏陈醋”40瓶,“小磨香油”60瓶,才能使所花费用最少,最少费用是1980元.
一、单选题
1.已知一次函数的图象如图,则下列说法正确的是( )
A. B.当时,
C.函数值y随自变量x的增大而减小 D.图象与y轴交于点
2.数学课上,老师在黑板上画出了菱形,并以点为圆心,的长为半径画弧,交直线于点,连接,关于四边形的形状,让同学们进行讨论,小明认为:只有当时,四边形是菱形;小红认为:当时,四边形是正方形,小刚认为:四边形是菱形,且,与的度数无关,下列判断正确的是( )
A.小明和小红正确,小刚错误 B.小红和小刚正确,小明错误
C.小明和小刚错误,小红正确 D.小明和小红错误,小刚正确
3.已知菱形的周长为,两条对角线的和为6,则菱形的面积为( )
A.2 B. C.3 D.4
4.规定表示不大于的最大整数,例如,,.那么函数的图象为( )
A. B.
C. D.
5.已知:平行四边形的顶点,点在轴的正半轴上,按以下步骤作图:
①以点为圆心,适当长为半径画弧,分别交于点,交于点.
②分别以点,为圆心,大于的长为半径画弧,两弧在内相交于点
③画射线,交于点,则点的坐标为( )
A. B. C. D.
6.如果最简二次根式与可以进行合并,则的值为( )
A.7 B.16 C.25 D.81
7.如图,在矩形中,,,动点从点出发,沿路线做匀速运动,那么面积的与点运动的路程之间的函数图像大致是( )
A. B.
C. D.
8.平面直角坐标系中,过点(-2,3)的直线经过一、二、三象限,若点(0,),(-1,),(,-1)都在直线上,则下列判断正确的是( )
A. B. C. D.
9.在中.是上一点,平分,且是的中点,则下列结论:①;②;③;④,其中正确的是( )
A.①② B.②④ C.③④ D.①②④
10.如图,E,F分别是平行四边形的边,上的点,与相交于点P,与相交于点Q,若,,,则阴影部分的面积为( )
A. B. C. D.
二、填空题
11.如图,正方形ABCD的边长为2,点E为边BC的中点,点P在对角线BD上移动,则PE+PC的最小值是 .
12.若最简二次根式与是同类二次根式,则x的值为 .
13.在四边形中,,给出下列4组条件:①,②,③,④.其中,不能得到“四边形是平行四边形”的条件是 .(只填序号)
14.为了响应学校“书香校园”建设,阳光班的同学们积极捐书,其中宏志学习小组的6名同学捐书册数分别是:5,7,x,8,4,6.已知他们平均每人捐6本,则这组数据的中位数是 .
15.矩形中,,是的中点,点在直线上,且,若与关于直线对称,则的长为 .
三、解答题
16.一条笔直的公路上依次有A、B、C三地,甲车从A地驶往C地,乙车从A地驶往B地,修好后立即以原速的两倍继续前进到达B地;如图是甲、乙两车与A地的距离y(千米)(小时)之间的大致图象.
(1)求B、C两地之间的距离;
(2)什么时候乙追上甲;
(3)当两车相距40千米时,甲车行驶了多长时间.
17.如图,在中,,,E,F分别为,的中点,过点B作的平行线与的延长线交于点D,连接,.
(1)求证:四边形为菱形;
(2)若,求四边形的面积.
18.小明对菱形的作法非常感兴趣,他根据所学的知识,利用直尺和圆规,在内分别以,为圆心,以的长为半径画弧,分别交,于点,,快速地作出一个菱形,如图()所示,根据小明的尺规作图过程,解决下列问题.
(1)小明用到的作图依据是( )
.一组对边平行且相等的四边形是菱形
.两组对边分别相等的四边形是菱形
.有一组邻边相等的平行四边形是菱形
.对角线互相垂直的平行四边形是菱形
(2)请在图()内运用另一种尺规作图的方法作出菱形,并证明你的结论.(保留作图痕迹,不写作法)
19.如图,在平行四边形ABCD中,AE平分∠DAB,已知CE=6,BE=8,DE=10.
(1)求BC的长;
(2)若∠CBE=36°,求∠ADC.
20.某学校计划组织452人参加社会实践活动,与某汽车租赁公司接洽后,得知该公司有型和型两种客车,它们的载客量和租金如下表所示.
A型客车 B型客车
载客量/(人辆) 45 26
租金/(元/辆) 400 240
经测算,租用型和型客车共13辆较为合理.设租用型客车辆.
(1)用含的代数式填写下表.
车量数/辆 载客量/人 租金/元
A型客车
B型客车
(2)采用怎样的租车方案可以使总的租车费用最低?最低为多少?
21.如图,在四边形ABCD中,AD∥BC,∠B=∠C,求证:AB=CD.
22.已知,如图,在平行四边形ABCD中,E、F分别为边AB、CD的中点,对角线的中点,对角线BD平分.
(1)求证:四边形BEDF为菱形;
(2)若AG//DB交CB的延长线于G,求证:四边形AGBD为矩形.
23.皇家驿站今年五一期间吸引了各地的游客前来观光,驻马店特产“伏陈醋”和“小磨香油”等也大受欢迎.某经销商抓住商机,计划购进某种包装的“伏陈醋”和“小磨香油”共100瓶,已知购进10瓶“伏陈醋”和20瓶“小磨香油”共需620元,购进30瓶“伏陈醋”和40瓶“小磨香油”共需1360元.
(1)每瓶“伏陈醋”和“小磨香油”的进价分别是多少元?
(2)结合游客的实际需求,该经销商决定购进“伏陈醋”的数量不超过“小磨香油”数量的,请你帮他计算如何进货才能使所花费用最少,最少费用是多少元?
参考答案
1.D
解:根据一次函数图像可知:函数值y随自变量x的增大而增大,,即A、C选项错误;由于k的值不确定,则一次函数与x轴交点坐标不确定,故B选项错误;当时,,即图象与y轴交于点,则D选项正确,符合题意.
故选:D.
2.D
解:∵菱形,
∴,,,
∴,,
由作图可得:,
∴,
∴四边形为菱形;为等边三角形,
∴,
∴,
∴小明认为:只有当时,四边形是菱形;说法错误;
小刚认为:四边形是菱形,且,与的度数无关,说法正确;
当时,而,
∴四边形不是正方形,
小红认为:当时,四边形是正方形,说法错误;
故选D
3.D
解:如图
四边形ABCD是菱形,AC+BD=6,菱形的周长为,
∴AB=,AC⊥BD,AO=AC,BO=BD,
∴AO+BO=3,
∴AO2+BO2=AB2,(AO+BO)2=9,
即AO2+BO2=5,AO2+2AO BO+BO2=9,
∴2AO BO=4,
∴菱形的面积=AC BD=2AO BO=4;
故选:D.
4.A
解:由已知得:当0≤x<1时,y=[x]=0,
当1≤x<2时,y=[x]=1,
当2≤x<3时,y=[x]=2,
当-1≤x<0时,y=[x]=-1,
当-2≤x<-1时,y=[x]=-2,
……
由以上可得A选项符合题意,
故选:A.
5.A
解:交轴于点,如图,
由作法得平分,
,
四边形为平行四边形,
∴,
,
,
设,则,
,
,,
,
,
在中,,
解得,
点坐标为.
故选:A.
6.D
解:最简二次根式与可以合并,
,
解得:,
∴
故选:D.
7.B
解:当点在线段上运动时,
∵,线段的长度将随着点沿路线运动的过程中而增大,
∴的面积随点的增大而增大,
当点与点重合时,
∵,,
∴,
当点在线段上运动时,的底边,边上的高的长是,
∴,
即此时的面积为定值,不随点的变化而变化,
∴符合题意的是B选项所表示的图像.
故选:B.
8.D
解:根据直线l经过第一、二、三象限且过点(-2,3),所以y随x的增大而增大.
因为-2<-1<0,所以3
故选D.
9.C
解:延长AD,交FE的延长线于点M,
∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠M=∠EFC,
∵E是CD的中点,
∴DE=CE,
在△DEM和△CEF中,
,
∴△DEM≌△CEF(AAS),
∴EM=EF,
∵AE平分∠FAD,
∴AM=AF,AE⊥EF.
即AF=AD+DM=CF+AD;故③,④正确,②错误.
∵AF不一定是∠BAD的角平分线,
∴AB不一定等于BF,故①错误.
故选:C.
10.C
解:连接、两点,过点作于点,
∵,,
∴,
∵四边形是平行四边形,
∴,
∴的边上的高与的边上的高相等,的边上的高与的边上的高相等,
∴,,
∴,即,
,即,
∵,,
∴,,
∴,
∴阴影部分的面积.
故选:C.
11.
解:如图,连接AE,
∵点C关于BD的对称点为点A,
∴PE+PC=PE+AP,
根据两点之间线段最短可得AE就是AP+PE的最小值,
∵正方形ABCD的边长为2,E是BC边的中点,
∴BE=1,
∴AE=.
故答案为:.
12.2.
∵最简二次根式与是同类二次根式,
∴x2﹣2=2x﹣2,
解得:x1=0,x2=2,
当x=0时与是无意义,
所以x=0舍去,
故答案为:2.
13.②
①,则一组对边平行且相等,可得到四边形是平行四边形,不符合题意;
②,无法得到四边形是平行四边形,符合题意;
③,两组对边分别平行,可得到四边形是平行四边形,不符合题意;
④,则此两角都是的补角,而与为同旁内角互补,可推出,两组对边分别平行,可得到四边形是平行四边形,不符合题意;
故答案为:②
14.6
由题意可得:=6,可知:x=6,将该数据从小到大排列得:4,5,6,6,7,8,故中位数为=6,故答案为6.
15.或
解:如图①,
与关于直线对称,
,
四边形是矩形,
,
,
;
如图②,
与关于直线对称,
,
四边形是矩形,
,
,
,
,
,
则的长为或.
故答案为:或.
16.(1)60千米
(2)出发后4.5小时
(3)或3.5或小时
(1)乙前面的速度为:(千米/小时),
乙后来的速度为:(千米/小时),
(千米),
答:B、C两地之间的距离为60千米;
(2)甲的速度为:(千米/小时),
设乙t小时追上甲,
根据题意得,
解得,
答:出发后4.5小时乙追上甲;
(3)当时,两车距离小于40,
①当时,
设甲距离A地的距离y(千米)与出发时间x(小时)之间的关系式为,
代入可得,
,
,解得;
②当时,
由(1)可得,A、B两地之间的距离为:,
设乙与A地距离与出发时间x之间的函数关系式为,
代入和
得,
解得,
,
解方程得(不合题意,舍去),
解方程得;
③当时,
解方程得.
答:当两车相距40千米时,甲车行驶了或3.5或小时.
17.(1)见解析;
(2)四边形的面积为.
(1)证明:∵,
∴,
∵为中点,
∴,
在和中
∴(ASA),
∴,
∵,
∴四边形是平行四边形,
∵为中点,为中点,
∴,
∵,
∴,
即,
∴四边形为菱形;
(2)解:∵,E,F分别为,的中点,
∴,,
∵,
∴,
∴,
在中,由勾股定理得:,
解得:,
∵,,
∴,,
∴四边形的面积为:
.
即:四边形的面积为.
18.(1)C;
(2)作图、证明见解析.
(1)解:根据作图,,
∵四边形是平行四边形,
∴,即,
∵,
∴四边形是平行四边形,
∵,
∴平行四边形是菱形,
用到的作图依据有一组对边平行且相等的四边形是平行四边形,有一组邻边相等的平行四边形是萎形,
故选:C;
(2)解:连接,作的中垂线交于,则四边形是菱形,
理由:由作图可知:,,,
∵四边形是平行四边形,
∴,
∴,
∵,,
∴,
∴,
∴四边形是平行四边形,
∵,
∴四边形是菱形
19.(1)BC=10;(2)126°.
解:(1)∵四边形ABCD是平行四边形,
∴AD=BC,DC∥AB,
∴∠DEA=∠EAB,
∵AE平分∠DAB,
∴∠DAE=∠EAB,
∴∠DAE=∠DEA,
∴AD=DE=10,
∴BC=10;
(2)∵CE=6,BE=8,BC=10,
∴CE2+BE2=62+82=100=BC2,
∴△BCE是直角三角形,且∠BEC=90°,
∴∠C=90°﹣∠CBE=90°﹣36°=54°,
∵AD∥BC,
∴∠D=180°﹣∠C=180°﹣54°=126°.
20.(1);
(2)租型车6辆、型车7辆时,总的租车费用最低,最低为4080元
(1)解:设租用型客车辆,则租用型客车辆,
型车的载客量,租金为.
故答案为:;.
(2)设租车的总费用为元,则有:.
由已知得:,
解得:.
在中,
当时,取最小值,最小值为4080元.
故租型车6辆、型车7辆时,总的租车费用最低,最低为4080元.
21.见解析
过点D作DF∥AB,
∵AD∥BC,
∴四边形ABFD是平行四边形,
∴AB=DF,∠DFC=∠B,
∵∠B=∠C,
∴∠DFC=∠C,
∴DF=DC,
∴AB=CD.
22.(1)见解析
(2)见解析
(1)证明:∵四边形ABCD是平行四边形,
∴AD=BC,ABCD,
∵E、F分别为边AB、CD的中点,
∴DF=EB,DFEB,
∴四边形DEBF是平行四边形,
∵DB平分∠EDF,
∴∠EDB=∠FDB,
∵DFEB,
∴∠FDB=∠EBD,
∴DE=BE,
又∵四边形DEBF是平行四边形,
∴四边形DEBF是菱形.
(2)证明:连接EF交BD于点O,
∵四边形DEBF是菱形,
∴EF⊥DB,OD=OB,
又∵E为AB的中点,
∴OEAD,
∴AD⊥BD,
∴∠ADB=90°,
∵ADBG,AGBD,
∴四边形AGBD为平行四边形,
∵∠ADB=90°,
∴四边形AGBD为矩形.
23.(1)每瓶“伏陈醋”的进价是12元,每瓶“小磨香油”的进价是25元
(2)购进“伏陈醋”40瓶,“小磨香油”60瓶,才能使所花费用最少,最少费用是1980元
(1)设每瓶“伏陈醋”的进价是元,每瓶“小磨香油”的进价是元,
根据题意得:,
解得,
每瓶“伏陈醋”的进价是12元,每瓶“小磨香油”的进价是25元;
(2)设购进“伏陈醋” 瓶,则购进“小磨香油” 瓶,
购进“伏陈醋”的数量不超过“小磨香油”数量的,
,
解得:,
设他所花费用为元,
根据题意得,
,
随增大而减小,
当时,取最小值(元,
此时,
购进“伏陈醋”40瓶,“小磨香油”60瓶,才能使所花费用最少,最少费用是1980元.
同课章节目录
