深圳市红桂中学等学校2025届九年级上学期开学考试数学试卷(含答案)
文档属性
| 名称 | 深圳市红桂中学等学校2025届九年级上学期开学考试数学试卷(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 958.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-26 10:46:36 | ||
图片预览

文档简介
广东省深圳市红桂中学等校2024-2025学年九年级上学期开学考试数学试题
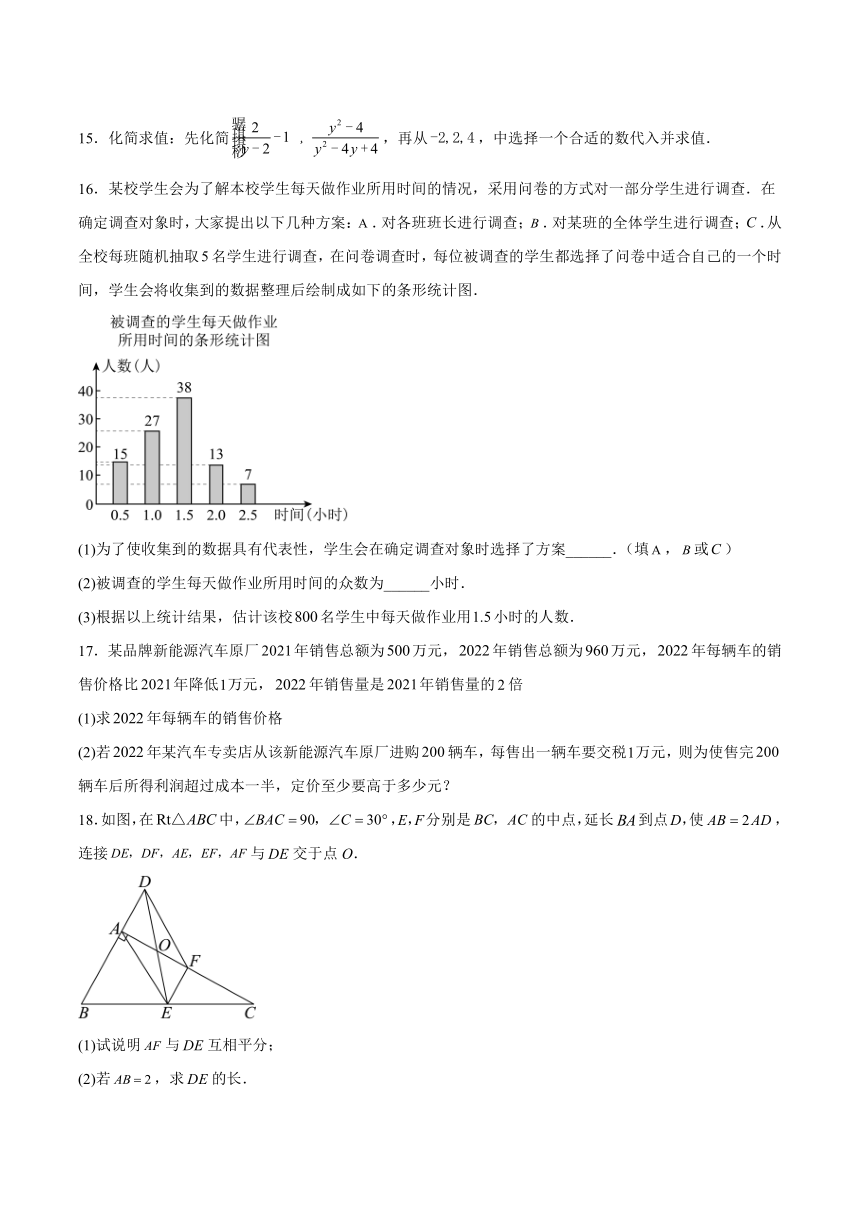
学校:___________姓名:___________班级:___________考号:___________
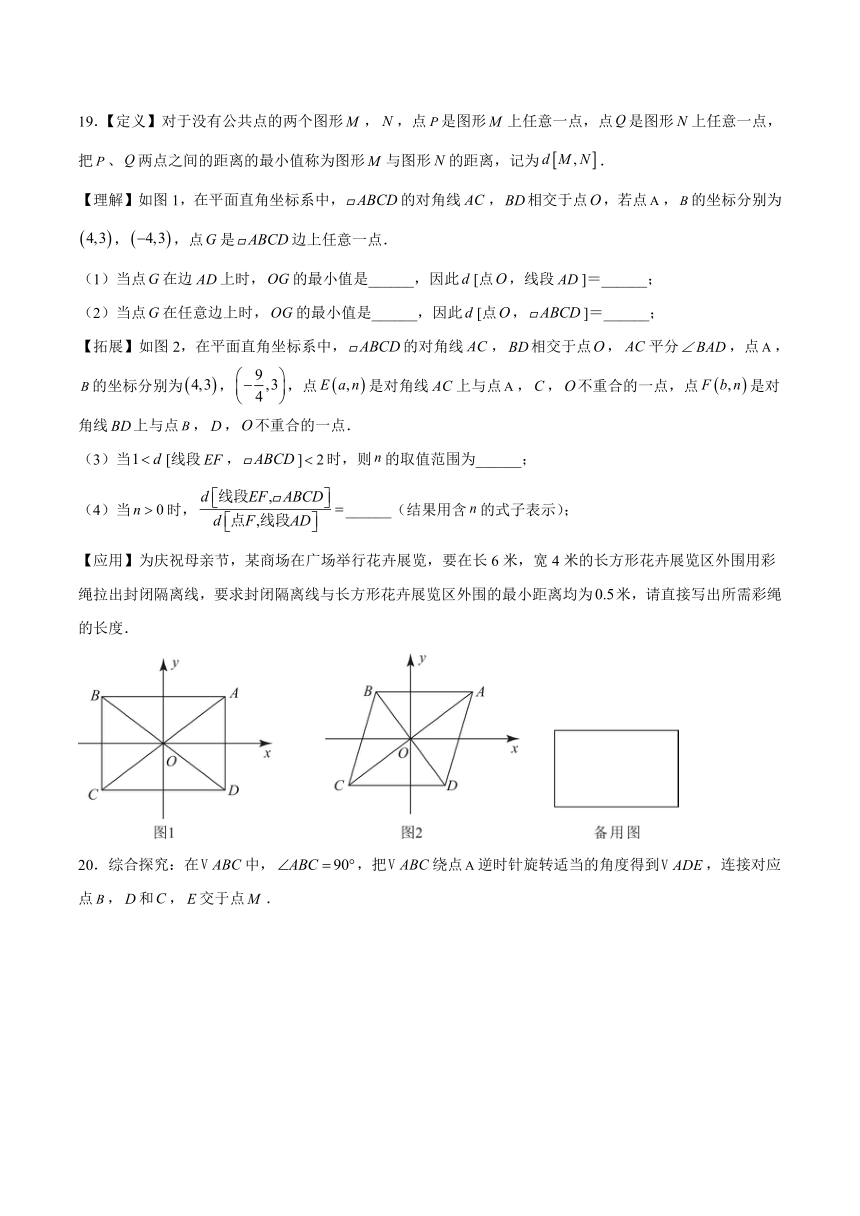
一、单选题
1.下列式子:①;②;③;④;⑤.其中是不等式的有( )
A.2个 B.3个 C.4个 D.5个
2.下列博物馆的图标中,既是轴对称图形又是中心对称图形的是( )
A. B. C. D.
3.下列各组线段中,能组成直角三角形的是( )
A. B. C.1,2,2 D.2,3,5
4.将多项式“”因式分解,结果为,则“?”是( )
A.3 B. C.9 D.
5.若代数式有意义,则实数x的取值范围是( )
A. B.且 C. D.且
6.如图,在平行四边形中,平分交于点E,若,,则的长为( )
A.3 B.4 C.5 D.6
7.若关于x的分式方程有增根,则a的值为( )
A.5 B. C.4 D.
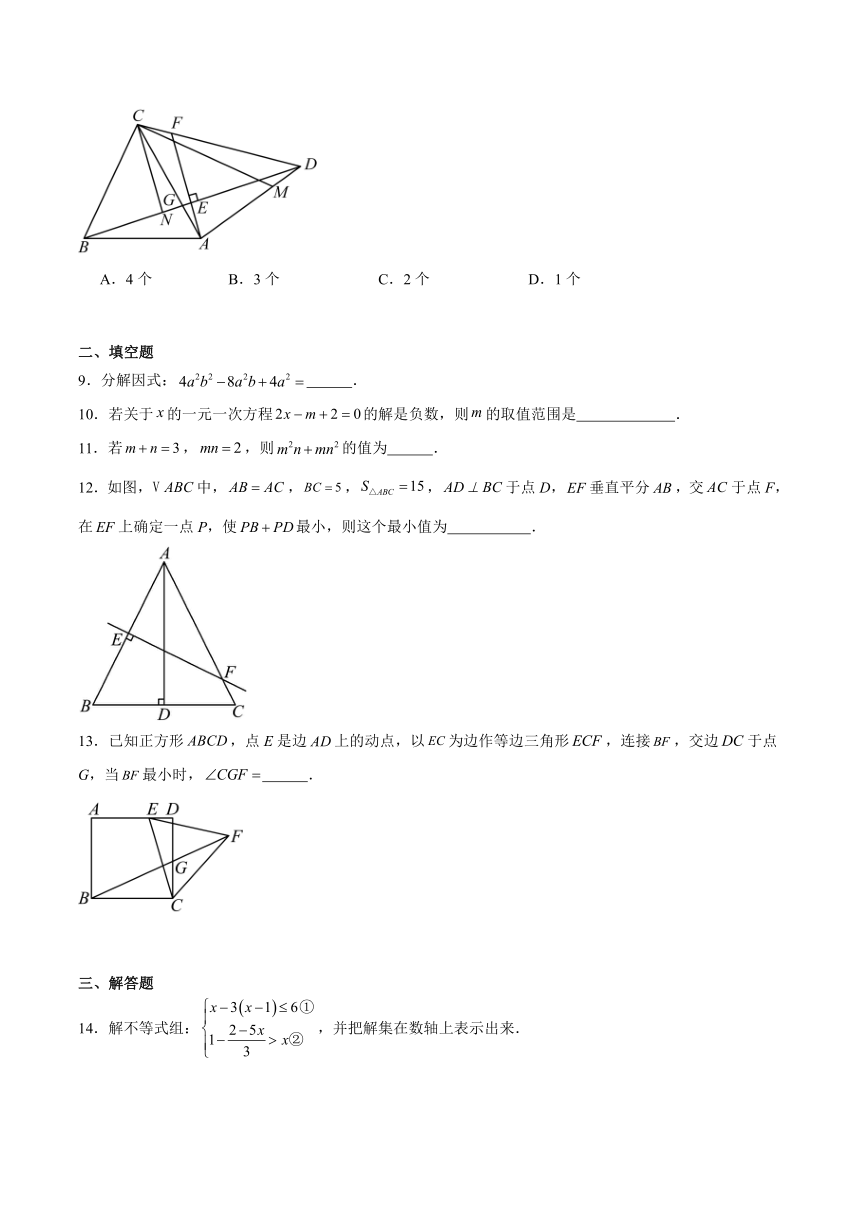
8.如图,在等边中,以A为直角顶点作等腰直角,分别交、于点E、F,N为线段上一动点,M为线段上一动点,且,以下4个结论:①;②;③;④当的值最小时,.正确的个数为( )
A.4个 B.3个 C.2个 D.1个
二、填空题
9.分解因式: .
10.若关于的一元一次方程的解是负数,则的取值范围是 .
11.若,,则的值为 .
12.如图,中,,,,于点D,垂直平分,交于点F,在上确定一点P,使最小,则这个最小值为 .
13.已知正方形,点E是边上的动点,以为边作等边三角形,连接,交边于点G,当最小时, .
三、解答题
14.解不等式组:,并把解集在数轴上表示出来.
15.化简求值:先化简,再从,中选择一个合适的数代入并求值.
16.某校学生会为了解本校学生每天做作业所用时间的情况,采用问卷的方式对一部分学生进行调查.在确定调查对象时,大家提出以下几种方案:.对各班班长进行调查;.对某班的全体学生进行调查;.从全校每班随机抽取名学生进行调查,在问卷调查时,每位被调查的学生都选择了问卷中适合自己的一个时间,学生会将收集到的数据整理后绘制成如下的条形统计图.
(1)为了使收集到的数据具有代表性,学生会在确定调查对象时选择了方案______.(填,或)
(2)被调查的学生每天做作业所用时间的众数为______小时.
(3)根据以上统计结果,估计该校名学生中每天做作业用小时的人数.
17.某品牌新能源汽车原厂年销售总额为万元,年销售总额为万元,年每辆车的销售价格比年降低万元,年销售量是年销售量的倍
(1)求年每辆车的销售价格
(2)若年某汽车专卖店从该新能源汽车原厂进购辆车,每售出一辆车要交税万元,则为使售完辆车后所得利润超过成本一半,定价至少要高于多少元?
18.如图,在中,,E,F分别是的中点,延长到点D,使,连接与交于点O.
(1)试说明与互相平分;
(2)若,求的长.
19.【定义】对于没有公共点的两个图形,,点是图形上任意一点,点是图形上任意一点,把、两点之间的距离的最小值称为图形与图形的距离,记为.
【理解】如图1,在平面直角坐标系中,的对角线,相交于点,若点,的坐标分别为,,点是边上任意一点.
(1)当点在边上时,的最小值是______,因此[点,线段]=______;
(2)当点在任意边上时,的最小值是______,因此[点,]=______;
【拓展】如图2,在平面直角坐标系中,的对角线,相交于点,平分,点,的坐标分别为,,点是对角线上与点,,不重合的一点,点是对角线上与点,,不重合的一点.
(3)当[线段,]时,则的取值范围为______;
(4)当时,______(结果用含的式子表示);
【应用】为庆祝母亲节,某商场在广场举行花卉展览,要在长6米,宽4米的长方形花卉展览区外围用彩绳拉出封闭隔离线,要求封闭隔离线与长方形花卉展览区外围的最小距离均为米,请直接写出所需彩绳的长度.
20.综合探究:在中,,把绕点逆时针旋转适当的角度得到,连接对应点,和,交于点.
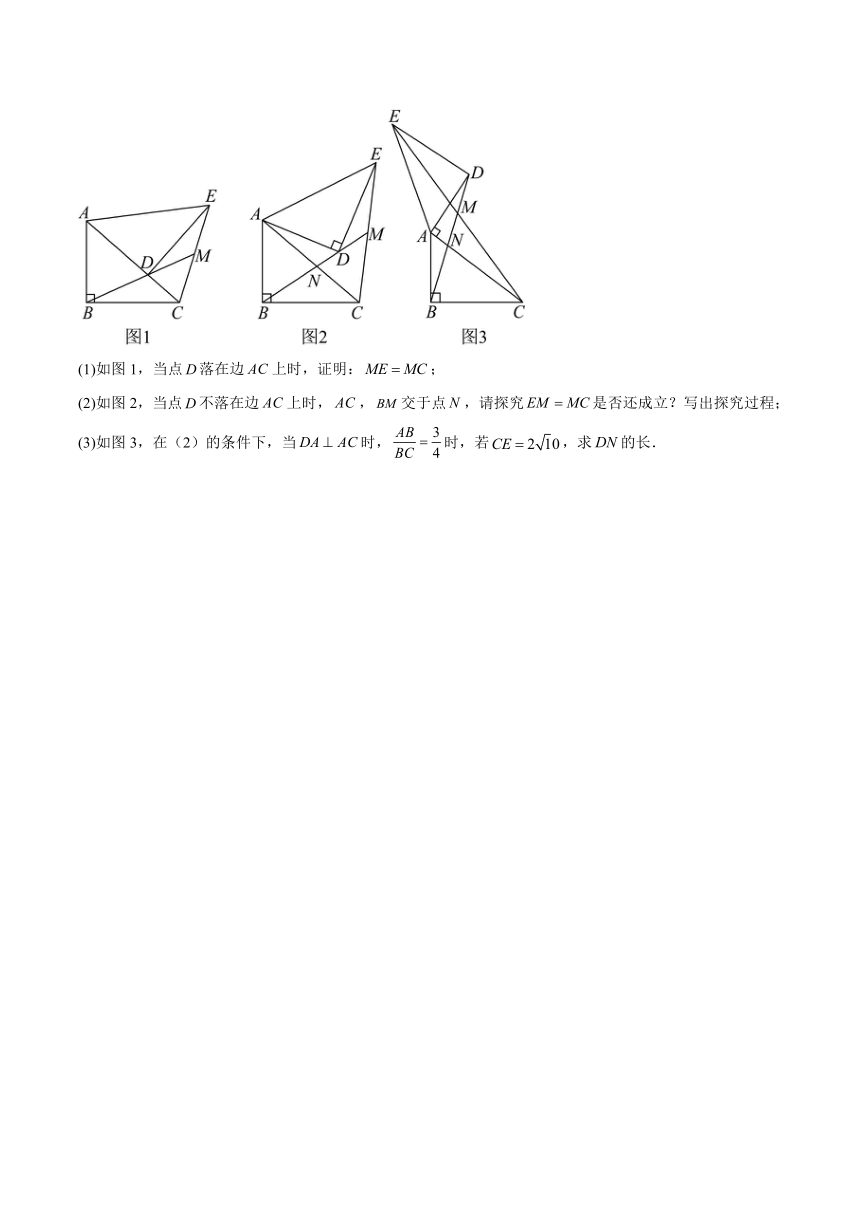
(1)如图1,当点落在边上时,证明:;
(2)如图2,当点不落在边上时,,交于点,请探究是否还成立?写出探究过程;
(3)如图3,在(2)的条件下,当时,时,若,求的长.
参考答案
题号 1 2 3 4 5 6 7 8
答案 B B A C B C B A
9.
10.
11.6
12.6
13./120度
14.解:解不等式①得:
解不等式②得:
∴此不等式组的解集为:
解集在数轴上表示为:
15.解:原式
;
,
,
当时,原式.
16.(1)解:为了使收集到的数据具有代表性,学生会在确定调查对象时选择了方案C;
(2)众数是:1.5小时;
(3)(人).
则估计该校800名学生中每天做作业用1.5小时的人数是304人.
17.(1)根据题意,设年每辆车的销售价格为万元,列方程可得:
;
解得:
答:年每辆车的销售价格为万元.
(2)解:设定价至少要万元;根据题意列不等式,
解得:,
答:为使售完辆车后所得利润超过成本一半,定价至少要高于万元.
18.(1)解:∵E,F分别是的中点,
∴,,
∵,
∴,
∴四边形是平行四边形,
∴与互相平分.
(2)解:∵,
∴,
∵,
∴,
由勾股定理得,,
∴,,
由勾股定理得,,
∵四边形是平行四边形,
∴,
∴的长为.
19.(1)∵,,四边形是平行四边形,
∴根据题意可知,当点在边上时,即时
∴ 的最小值是,因此[点,线段]=,
故答案为:;
(2)∵ ,,四边形 是平行四边形,
∴根据题意可知,当点在边任意边上时,即或时,
∴的最小值是,因此[点, ]=,
故答案为:;
(3)如图,
∵四边形是平行四边形,
∴,
∴,
∴平分,
∴,
∴,
∴,
∴四边形是菱形,
∴平分和,
∴线段到四边形的距离为, [线段,]=,
∴,解得:或,
故答案为:或,
(4)由(3)得:四边形是菱形,过作于点,交于点,作于点,如图,则有,
∴,
∴,
故答案为:,
(4)由题意得,要求封闭隔离线与长方形花卉展览区外围的最小距离均为米,则如下图,
则所需彩绳的长度为:.
20.(1)证明:根据题意,把绕点逆时针旋转适当的角度得到,
∴,,,
∴,,
又∵,
∴,
∵,
∴,
∴,
∵,
∴,
∴,
∴;
(2)如下图,过点作交的延长线于点,连接,
∴,
∵由旋转可知,,,,
∴,
∴,
∴,
∴,
∴,
∴,
∴四边形为平行四边形,
∴;
(3)连接,如下图,
由旋转的性质可得,,,,
∴,
∵,
∴,
∴,
∴,
∵,
∴,
∴,
∵,
∴可设,,
则,,,,
∴,
∵
∴,
∴,
由(2)知,
又∵,
∴,
∴,
∴,
∵,,
∴,
∴在中,可有,
即,解得,
∴.
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.下列式子:①;②;③;④;⑤.其中是不等式的有( )
A.2个 B.3个 C.4个 D.5个
2.下列博物馆的图标中,既是轴对称图形又是中心对称图形的是( )
A. B. C. D.
3.下列各组线段中,能组成直角三角形的是( )
A. B. C.1,2,2 D.2,3,5
4.将多项式“”因式分解,结果为,则“?”是( )
A.3 B. C.9 D.
5.若代数式有意义,则实数x的取值范围是( )
A. B.且 C. D.且
6.如图,在平行四边形中,平分交于点E,若,,则的长为( )
A.3 B.4 C.5 D.6
7.若关于x的分式方程有增根,则a的值为( )
A.5 B. C.4 D.
8.如图,在等边中,以A为直角顶点作等腰直角,分别交、于点E、F,N为线段上一动点,M为线段上一动点,且,以下4个结论:①;②;③;④当的值最小时,.正确的个数为( )
A.4个 B.3个 C.2个 D.1个
二、填空题
9.分解因式: .
10.若关于的一元一次方程的解是负数,则的取值范围是 .
11.若,,则的值为 .
12.如图,中,,,,于点D,垂直平分,交于点F,在上确定一点P,使最小,则这个最小值为 .
13.已知正方形,点E是边上的动点,以为边作等边三角形,连接,交边于点G,当最小时, .
三、解答题
14.解不等式组:,并把解集在数轴上表示出来.
15.化简求值:先化简,再从,中选择一个合适的数代入并求值.
16.某校学生会为了解本校学生每天做作业所用时间的情况,采用问卷的方式对一部分学生进行调查.在确定调查对象时,大家提出以下几种方案:.对各班班长进行调查;.对某班的全体学生进行调查;.从全校每班随机抽取名学生进行调查,在问卷调查时,每位被调查的学生都选择了问卷中适合自己的一个时间,学生会将收集到的数据整理后绘制成如下的条形统计图.
(1)为了使收集到的数据具有代表性,学生会在确定调查对象时选择了方案______.(填,或)
(2)被调查的学生每天做作业所用时间的众数为______小时.
(3)根据以上统计结果,估计该校名学生中每天做作业用小时的人数.
17.某品牌新能源汽车原厂年销售总额为万元,年销售总额为万元,年每辆车的销售价格比年降低万元,年销售量是年销售量的倍
(1)求年每辆车的销售价格
(2)若年某汽车专卖店从该新能源汽车原厂进购辆车,每售出一辆车要交税万元,则为使售完辆车后所得利润超过成本一半,定价至少要高于多少元?
18.如图,在中,,E,F分别是的中点,延长到点D,使,连接与交于点O.
(1)试说明与互相平分;
(2)若,求的长.
19.【定义】对于没有公共点的两个图形,,点是图形上任意一点,点是图形上任意一点,把、两点之间的距离的最小值称为图形与图形的距离,记为.
【理解】如图1,在平面直角坐标系中,的对角线,相交于点,若点,的坐标分别为,,点是边上任意一点.
(1)当点在边上时,的最小值是______,因此[点,线段]=______;
(2)当点在任意边上时,的最小值是______,因此[点,]=______;
【拓展】如图2,在平面直角坐标系中,的对角线,相交于点,平分,点,的坐标分别为,,点是对角线上与点,,不重合的一点,点是对角线上与点,,不重合的一点.
(3)当[线段,]时,则的取值范围为______;
(4)当时,______(结果用含的式子表示);
【应用】为庆祝母亲节,某商场在广场举行花卉展览,要在长6米,宽4米的长方形花卉展览区外围用彩绳拉出封闭隔离线,要求封闭隔离线与长方形花卉展览区外围的最小距离均为米,请直接写出所需彩绳的长度.
20.综合探究:在中,,把绕点逆时针旋转适当的角度得到,连接对应点,和,交于点.
(1)如图1,当点落在边上时,证明:;
(2)如图2,当点不落在边上时,,交于点,请探究是否还成立?写出探究过程;
(3)如图3,在(2)的条件下,当时,时,若,求的长.
参考答案
题号 1 2 3 4 5 6 7 8
答案 B B A C B C B A
9.
10.
11.6
12.6
13./120度
14.解:解不等式①得:
解不等式②得:
∴此不等式组的解集为:
解集在数轴上表示为:
15.解:原式
;
,
,
当时,原式.
16.(1)解:为了使收集到的数据具有代表性,学生会在确定调查对象时选择了方案C;
(2)众数是:1.5小时;
(3)(人).
则估计该校800名学生中每天做作业用1.5小时的人数是304人.
17.(1)根据题意,设年每辆车的销售价格为万元,列方程可得:
;
解得:
答:年每辆车的销售价格为万元.
(2)解:设定价至少要万元;根据题意列不等式,
解得:,
答:为使售完辆车后所得利润超过成本一半,定价至少要高于万元.
18.(1)解:∵E,F分别是的中点,
∴,,
∵,
∴,
∴四边形是平行四边形,
∴与互相平分.
(2)解:∵,
∴,
∵,
∴,
由勾股定理得,,
∴,,
由勾股定理得,,
∵四边形是平行四边形,
∴,
∴的长为.
19.(1)∵,,四边形是平行四边形,
∴根据题意可知,当点在边上时,即时
∴ 的最小值是,因此[点,线段]=,
故答案为:;
(2)∵ ,,四边形 是平行四边形,
∴根据题意可知,当点在边任意边上时,即或时,
∴的最小值是,因此[点, ]=,
故答案为:;
(3)如图,
∵四边形是平行四边形,
∴,
∴,
∴平分,
∴,
∴,
∴,
∴四边形是菱形,
∴平分和,
∴线段到四边形的距离为, [线段,]=,
∴,解得:或,
故答案为:或,
(4)由(3)得:四边形是菱形,过作于点,交于点,作于点,如图,则有,
∴,
∴,
故答案为:,
(4)由题意得,要求封闭隔离线与长方形花卉展览区外围的最小距离均为米,则如下图,
则所需彩绳的长度为:.
20.(1)证明:根据题意,把绕点逆时针旋转适当的角度得到,
∴,,,
∴,,
又∵,
∴,
∵,
∴,
∴,
∵,
∴,
∴,
∴;
(2)如下图,过点作交的延长线于点,连接,
∴,
∵由旋转可知,,,,
∴,
∴,
∴,
∴,
∴,
∴,
∴四边形为平行四边形,
∴;
(3)连接,如下图,
由旋转的性质可得,,,,
∴,
∵,
∴,
∴,
∴,
∵,
∴,
∴,
∵,
∴可设,,
则,,,,
∴,
∵
∴,
∴,
由(2)知,
又∵,
∴,
∴,
∴,
∵,,
∴,
∴在中,可有,
即,解得,
∴.
同课章节目录
