江西省横峰中学、铅山一中2016-2017学年高一9月假期验收数学试题 Word版含答案
文档属性
| 名称 | 江西省横峰中学、铅山一中2016-2017学年高一9月假期验收数学试题 Word版含答案 |  | |
| 格式 | zip | ||
| 文件大小 | 287.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-09-01 14:14:13 | ||
图片预览



文档简介
高考资源网(
www.),您身边的高考专家
高考资源网(
www.),您身边的高考专家
课改实验班暑期月考
数
学
注意事项:
1、考生务必将自己的姓名、考号、考试科目信息等填涂在答题卷上;
2、选择题、综合题均完成在答题卷上;
3、考试结束,监考人员将答题卷收回。
一、选择题:(本题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一个选项符合题意.)
1.已知集合A={x|-1<x<2},B={x|0<x<3},则A∪B等于( )
A.(-1,3)
B.(-1,0)
C.(0,2)
D.(2,3)
2.集合A={1,2,3,5},当x∈A时,若x-1A,x+1A,则称x为A的一个“孤立元素”,则A中孤立元素的个数为( )
A.1
B.2
C.3
D.4
3已知集合A={-1,},B={x|mx-1=0},若A∩B=B,则所有实数m组成的集合是( )
A.{-1,2}
B.{-,0,1}
C.{-1,0,2}
D.{-1,0,}
4.已知函数f(x)=则f(log25)等于( )
A.
B.
C.
D.
5.函数y=e|lnx|-|x-1|的图象大致是( )
6.设f(x)=1-(x-a)(x-b)(aA.aB.mC.aD.m7.定义在R上的函数f(x)既是奇函数,又是周期函数,T是它的一个正周期,若将该函数在区间[-T,T]上的零点个数记为n,则n可能为( )
A.0
B.1
C.3
D.5
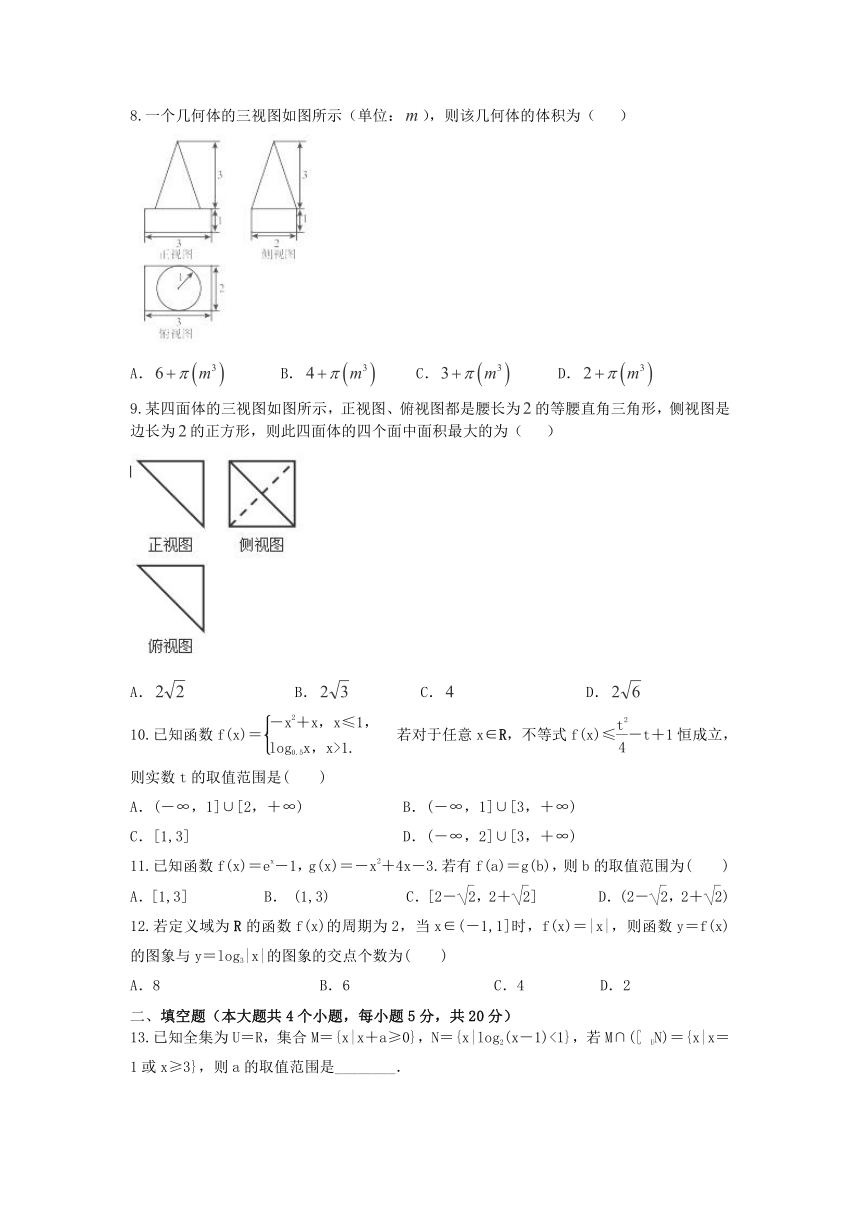
8.一个几何体的三视图如图所示(单位:),则该几何体的体积为(
)
A.
B.
C.
D.
9.某四面体的三视图如图所示,正视图、俯视图都是腰长为的等腰直角三角形,侧视图是边长为的正方形,则此四面体的四个面中面积最大的为(
)
A.
B.
C.
D.
10.已知函数f(x)=若对于任意x∈R,不等式f(x)≤-t+1恒成立,则实数t的取值范围是( )
A.(-∞,1]∪[2,+∞)
B.(-∞,1]∪[3,+∞)
C.[1,3]
D.(-∞,2]∪[3,+∞)
11.已知函数f(x)=ex-1,g(x)=-x2+4x-3.若有f(a)=g(b),则b的取值范围为( )
A.[1,3]
B.
(1,3)
C.[2-,2+]
D.(2-,2+)
12.若定义域为R的函数f(x)的周期为2,当x∈(-1,1]时,f(x)=|x|,则函数y=f(x)的图象与y=log3|x|的图象的交点个数为( )
A.8
B.6
C.4
D.2
二、填空题(本大题共4个小题,每小题5分,共20分)
13.已知全集为U=R,集合M={x|x+a≥0},N={x|log2(x-1)<1},若M∩( UN)={x|x=1或x≥3},则a的取值范围是________.
14.已知y=f(x)在(0,2)上是增函数,y=f(x+2)是偶函数,则f(1),f(),f()的大小关系是____________.(用“<”连接)
15.已知函数f(x)=满足f(0)=1,且有f(0)+2
f(-1)=0,那么函数g(x)=f(x)+x的零点有________个.
16.已知f(x)=|loga|x-1||(a>0,a≠1),若x1三、解答题(本大题共6小题,满分70分,解答应写出必要的文字说明、证明过程或演算步骤.)
17.(本小题满分10分)计算:
(1)
(2)已知,试计算:
18.(本小题满分12分)已知函数.
(1)求实数的取值范围,使在上为单调函数;
(2)求函数的最小值.
19.(本小题满分12分)已知函数
,函数.
(1)求函数与的解析式,并求出的定义域;
(2)设,试求函数的最值.
20.(本小题满分12分)
如图,在四棱锥P-ABCD中,AD=CD=AB,AB∥CD,AD⊥CD,PC⊥平面ABCD.
(1)求证:BC⊥平面PAC;
(2)若M为线段PA的中点,且过C,D,M三点的平面与PB交于点N,求PN
:
PB的值.
21.(本小题满分12分)
在如图所示的几何体中,四边形ABCD为平行四边形,∠ACD=90°,AB=1,AD=2,四边形ABEF为正方形,平面ABEF⊥平面ABCD,P为DF的中点,AN⊥CF,垂足为N.
(1)求证:BF∥平面PAC;
(2)求证:AN⊥平面CDF;
(3)求三棱锥B-CEF的体积.
22.(本小题满分12分)已知是偶函数,是奇函数.
(1)求的值;
(2)判断的单调性(不要求证明);
(3)若不等式在上恒成立,求实数的取值范围.
课改实验班暑期月考
数学参考答案
一、选择题(本大题共12小题,每小题5分,满分60分,每小题只有一个正确选项)
题号
1
2
3
4
5
6
7
8
9
10
11
12
答案
A
A
C
C
D
B
D
A
B
B
D
C
二、填空题(本大题共4小题,每小题5分,满分20分)
13、{-1}
14、f()
15、2
16、2
三、解答题(本大题共6小题,满分70分.解答应写出文字说明,证明过程或演算步骤.)
17.(本小题满分10分)
(1)(2)4
18.(本小题满分12分)
(1)的对称轴为又在上为单调函数,则
或,
或
.
…………
4分
(2) f(x)=x2+2ax+5=(x+a)2+5-a2.
函数的对称轴为x=-a.
当-a≤-1,即a≥1时,在上是增加的,f(x)min=f(-1)=6-2a.
当-1<-a<2,即-2f(x)min=f(-a)=5-a2.
当-a≥2,即a≤-2时,在上是减少的,f(x)min=f(2)=9+4a.
综上所述,函数的最小值为
…………12分
(本小题满分12分)
解
(1)设,则,于是有,
∴(),………4分
根据题意得
又由得
∴()………6分
(2)∵∴要使函数有意义,
必须∴,………………………8分
∴
()………………………10分
设,则是上增函数,
∴时=6,
时………………………12分
∴函数的最大值为13,最小值为6.
………12分
(本小题满分12分)
(1)证明 连接AC.不妨设AD=1,
因为AD=CD=AB,
所以CD=1,AB=2.
因为∠ADC=90°,所以AC=,∠CAB=45°.
在△ABC中,由余弦定理得BC=,
所以AC2+BC2=AB2.
所以BC⊥AC.
因为PC⊥平面ABCD,
BC 平面ABCD,
所以BC⊥PC.
又PC 平面PAC,AC 平面PAC,PC∩AC=C,
所以BC⊥平面PAC.………6分
(2)解
如图,因为AB∥CD,
CD 平面CDMN,AB 平面CDMN,
所以AB∥平面CDMN.
因为AB 平面PAB,
平面PAB∩平面CDMN=MN,
所以AB∥MN.
在△PAB中,因为M为PA的中点,
所以N为PB的中点,
即PN∶PB的值为.………12分
(本小题满分12分)
(1)证明
如图,连接BD交AC于O,连接PO.
∵PO是△BDF的中位线,
∴PO∥BF.
∵PO 平面ACP,BF 平面ACP,
∴BF∥平面PAC.………4分
(2)证明 ∵平面ABEF⊥平面ABCD,
交线为AB,AF⊥AB,AF 平面ABEF,
∴AF⊥平面ABCD.
∵CD 平面ABCD,∴AF⊥CD.
又∵CD⊥AC,AC∩AF=A,AC 平面ACF,AF 平面ACF,
∴CD⊥平面ACF,
∵AN 平面ACF,∴CD⊥AN.
∵AN⊥CF,CD∩CF=C,
且CF 平面CDF,CD 平面CDF,
∴AN⊥平面CDF.………8分
(3)解 ∵平面ABEF⊥平面ABCD,
交线为AB,CA⊥AB,CA 平面ABCD,
∴CA⊥平面ABEF,CA==,
∴V三棱锥B-CEF=V三棱锥C-BEF=S△BEF×CA=××1×1×=.………12分
22.(本小题满分12分)
解:(Ⅰ)由题意有:
可得----------------------------------------------------------------------------------------------(2分)
再由可得:----------------------------(4分)
(Ⅱ)在上为增函数.--------------------------------------------(6分)
(Ⅲ)由(Ⅱ)得:
即在恒成立-----------------------------------------------------------(8分)
为增函数,
即----------------------------------------------------------------------------------(12分)
投稿兼职请联系:2355394692
www.
投稿兼职请联系:2355394692
www.
www.),您身边的高考专家
高考资源网(
www.),您身边的高考专家
课改实验班暑期月考
数
学
注意事项:
1、考生务必将自己的姓名、考号、考试科目信息等填涂在答题卷上;
2、选择题、综合题均完成在答题卷上;
3、考试结束,监考人员将答题卷收回。
一、选择题:(本题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一个选项符合题意.)
1.已知集合A={x|-1<x<2},B={x|0<x<3},则A∪B等于( )
A.(-1,3)
B.(-1,0)
C.(0,2)
D.(2,3)
2.集合A={1,2,3,5},当x∈A时,若x-1A,x+1A,则称x为A的一个“孤立元素”,则A中孤立元素的个数为( )
A.1
B.2
C.3
D.4
3已知集合A={-1,},B={x|mx-1=0},若A∩B=B,则所有实数m组成的集合是( )
A.{-1,2}
B.{-,0,1}
C.{-1,0,2}
D.{-1,0,}
4.已知函数f(x)=则f(log25)等于( )
A.
B.
C.
D.
5.函数y=e|lnx|-|x-1|的图象大致是( )
6.设f(x)=1-(x-a)(x-b)(a
A.0
B.1
C.3
D.5
8.一个几何体的三视图如图所示(单位:),则该几何体的体积为(
)
A.
B.
C.
D.
9.某四面体的三视图如图所示,正视图、俯视图都是腰长为的等腰直角三角形,侧视图是边长为的正方形,则此四面体的四个面中面积最大的为(
)
A.
B.
C.
D.
10.已知函数f(x)=若对于任意x∈R,不等式f(x)≤-t+1恒成立,则实数t的取值范围是( )
A.(-∞,1]∪[2,+∞)
B.(-∞,1]∪[3,+∞)
C.[1,3]
D.(-∞,2]∪[3,+∞)
11.已知函数f(x)=ex-1,g(x)=-x2+4x-3.若有f(a)=g(b),则b的取值范围为( )
A.[1,3]
B.
(1,3)
C.[2-,2+]
D.(2-,2+)
12.若定义域为R的函数f(x)的周期为2,当x∈(-1,1]时,f(x)=|x|,则函数y=f(x)的图象与y=log3|x|的图象的交点个数为( )
A.8
B.6
C.4
D.2
二、填空题(本大题共4个小题,每小题5分,共20分)
13.已知全集为U=R,集合M={x|x+a≥0},N={x|log2(x-1)<1},若M∩( UN)={x|x=1或x≥3},则a的取值范围是________.
14.已知y=f(x)在(0,2)上是增函数,y=f(x+2)是偶函数,则f(1),f(),f()的大小关系是____________.(用“<”连接)
15.已知函数f(x)=满足f(0)=1,且有f(0)+2
f(-1)=0,那么函数g(x)=f(x)+x的零点有________个.
16.已知f(x)=|loga|x-1||(a>0,a≠1),若x1
17.(本小题满分10分)计算:
(1)
(2)已知,试计算:
18.(本小题满分12分)已知函数.
(1)求实数的取值范围,使在上为单调函数;
(2)求函数的最小值.
19.(本小题满分12分)已知函数
,函数.
(1)求函数与的解析式,并求出的定义域;
(2)设,试求函数的最值.
20.(本小题满分12分)
如图,在四棱锥P-ABCD中,AD=CD=AB,AB∥CD,AD⊥CD,PC⊥平面ABCD.
(1)求证:BC⊥平面PAC;
(2)若M为线段PA的中点,且过C,D,M三点的平面与PB交于点N,求PN
:
PB的值.
21.(本小题满分12分)
在如图所示的几何体中,四边形ABCD为平行四边形,∠ACD=90°,AB=1,AD=2,四边形ABEF为正方形,平面ABEF⊥平面ABCD,P为DF的中点,AN⊥CF,垂足为N.
(1)求证:BF∥平面PAC;
(2)求证:AN⊥平面CDF;
(3)求三棱锥B-CEF的体积.
22.(本小题满分12分)已知是偶函数,是奇函数.
(1)求的值;
(2)判断的单调性(不要求证明);
(3)若不等式在上恒成立,求实数的取值范围.
课改实验班暑期月考
数学参考答案
一、选择题(本大题共12小题,每小题5分,满分60分,每小题只有一个正确选项)
题号
1
2
3
4
5
6
7
8
9
10
11
12
答案
A
A
C
C
D
B
D
A
B
B
D
C
二、填空题(本大题共4小题,每小题5分,满分20分)
13、{-1}
14、f()
15、2
16、2
三、解答题(本大题共6小题,满分70分.解答应写出文字说明,证明过程或演算步骤.)
17.(本小题满分10分)
(1)(2)4
18.(本小题满分12分)
(1)的对称轴为又在上为单调函数,则
或,
或
.
…………
4分
(2) f(x)=x2+2ax+5=(x+a)2+5-a2.
函数的对称轴为x=-a.
当-a≤-1,即a≥1时,在上是增加的,f(x)min=f(-1)=6-2a.
当-1<-a<2,即-2
当-a≥2,即a≤-2时,在上是减少的,f(x)min=f(2)=9+4a.
综上所述,函数的最小值为
…………12分
(本小题满分12分)
解
(1)设,则,于是有,
∴(),………4分
根据题意得
又由得
∴()………6分
(2)∵∴要使函数有意义,
必须∴,………………………8分
∴
()………………………10分
设,则是上增函数,
∴时=6,
时………………………12分
∴函数的最大值为13,最小值为6.
………12分
(本小题满分12分)
(1)证明 连接AC.不妨设AD=1,
因为AD=CD=AB,
所以CD=1,AB=2.
因为∠ADC=90°,所以AC=,∠CAB=45°.
在△ABC中,由余弦定理得BC=,
所以AC2+BC2=AB2.
所以BC⊥AC.
因为PC⊥平面ABCD,
BC 平面ABCD,
所以BC⊥PC.
又PC 平面PAC,AC 平面PAC,PC∩AC=C,
所以BC⊥平面PAC.………6分
(2)解
如图,因为AB∥CD,
CD 平面CDMN,AB 平面CDMN,
所以AB∥平面CDMN.
因为AB 平面PAB,
平面PAB∩平面CDMN=MN,
所以AB∥MN.
在△PAB中,因为M为PA的中点,
所以N为PB的中点,
即PN∶PB的值为.………12分
(本小题满分12分)
(1)证明
如图,连接BD交AC于O,连接PO.
∵PO是△BDF的中位线,
∴PO∥BF.
∵PO 平面ACP,BF 平面ACP,
∴BF∥平面PAC.………4分
(2)证明 ∵平面ABEF⊥平面ABCD,
交线为AB,AF⊥AB,AF 平面ABEF,
∴AF⊥平面ABCD.
∵CD 平面ABCD,∴AF⊥CD.
又∵CD⊥AC,AC∩AF=A,AC 平面ACF,AF 平面ACF,
∴CD⊥平面ACF,
∵AN 平面ACF,∴CD⊥AN.
∵AN⊥CF,CD∩CF=C,
且CF 平面CDF,CD 平面CDF,
∴AN⊥平面CDF.………8分
(3)解 ∵平面ABEF⊥平面ABCD,
交线为AB,CA⊥AB,CA 平面ABCD,
∴CA⊥平面ABEF,CA==,
∴V三棱锥B-CEF=V三棱锥C-BEF=S△BEF×CA=××1×1×=.………12分
22.(本小题满分12分)
解:(Ⅰ)由题意有:
可得----------------------------------------------------------------------------------------------(2分)
再由可得:----------------------------(4分)
(Ⅱ)在上为增函数.--------------------------------------------(6分)
(Ⅲ)由(Ⅱ)得:
即在恒成立-----------------------------------------------------------(8分)
为增函数,
即----------------------------------------------------------------------------------(12分)
投稿兼职请联系:2355394692
www.
投稿兼职请联系:2355394692
www.
同课章节目录
