点到平面的距离的几种求法

点到平面的距离的几种求法
求‘点到平面的距离’是立体几何学习中不可忽视的一个基本问题，是近几年高考的一个热点．本文试通过对一道典型例题的多种解法的探讨，结合《立体几何》(必修本)中的概念、习题，概括出求‘点到平面的距离’的几种基本方法．
　
　
例：已知ＡＢＣＤ是边长为4的正方形，Ｅ、Ｆ分别是ＡＢ、ＡＤ的中点，ＧＣ垂直于ＡＢＣＤ所在平面，且ＧＣ＝２，求点B到平面ＥＦＧ的距离．
　
一、直接通过该点求点到平面的距离
　
１．直接作出所求之距离，求其长．
　
解法1．如图1，为了作出点B到平面EFG的距离，延长FE交ＣＢ的延长线于Ｍ，
连
结GM，作BN⊥BC，交GM于N，则有BN∥CG，BN⊥平面ABCD．作BP⊥EM，交EM于P，易证平面BPN⊥平面EFG．作BQ⊥PN，垂足为Q，则BQ⊥平面EFG．于
是BQ是点B到平面EFG的距离．易知BN＝，BP＝，PZ＝，由BQ·PN＝PB·BN，得BQ＝．
INCLUDEPICTURE
"http://www.cbe21.com/subject/maths/images/040601/2016/2016005.gif"
\
MERGEFORMATINET
　　　　　　　　　　
INCLUDEPICTURE
"http://www.cbe21.com/subject/maths/images/040601/2016/2016006.gif"
\
MERGEFORMATINET
图1　　　　　　　　　　　　　　　　　　　　　
图2
　２．不直接作出所求之距离，间接求之．
（１）利用二面角的平面角．
　
课本Ｐ．４２第4题，Ｐ．４６第2题、第4题给出了“二面角一个面内的一个点，它到棱的距离、到另一个面的距离与二面角的大小之间所满足的关系”．如图2，二面角Ｍ-ＣＤ-Ｎ的大小为α，Ａ∈Ｍ，ＡＢ⊥ＣＤ，ＡＢ＝ａ，点Ａ到平面Ｎ的距离ＡＯ＝ｄ，
则有ｄ＝ａｓｉｎα．
①
①中的α也就是二面角的大小，而并不强求要作出经过ＡＢ的二面角的平面角．
　
解法2．如图3，过Ｂ作ＢＰ⊥ＥＦ，交ＦＥ的延长线于Ｐ，易知ＢＰ＝，这就是点Ｂ到二面角Ｃ-ＥＦ-Ｇ的棱ＥＦ的距离．连结ＡＣ交ＥＦ于Ｈ，连结ＧＨ，易证∠ＧＨＣ就是二面角Ｃ-ＥＦ-Ｇ的平面角．∵
ＧＣ＝２，ＡＣ＝４，ＡＨ＝，∴
ＣＨ＝３，ＧＨ＝，ｓｉｎ∠ＧＨＣ＝，于是由①得所求之距离ｄ＝ＢＰ·ｓｉｎ∠ＧＨＣ＝·＝．解略．
INCLUDEPICTURE
"http://www.cbe21.com/subject/maths/images/040601/2016/2016011.gif"
\
MERGEFORMATINET
　　　　　　　　　
INCLUDEPICTURE
"http://www.cbe21.com/subject/maths/images/040601/2016/2016012.gif"
\
MERGEFORMATINET
　
图3
图4
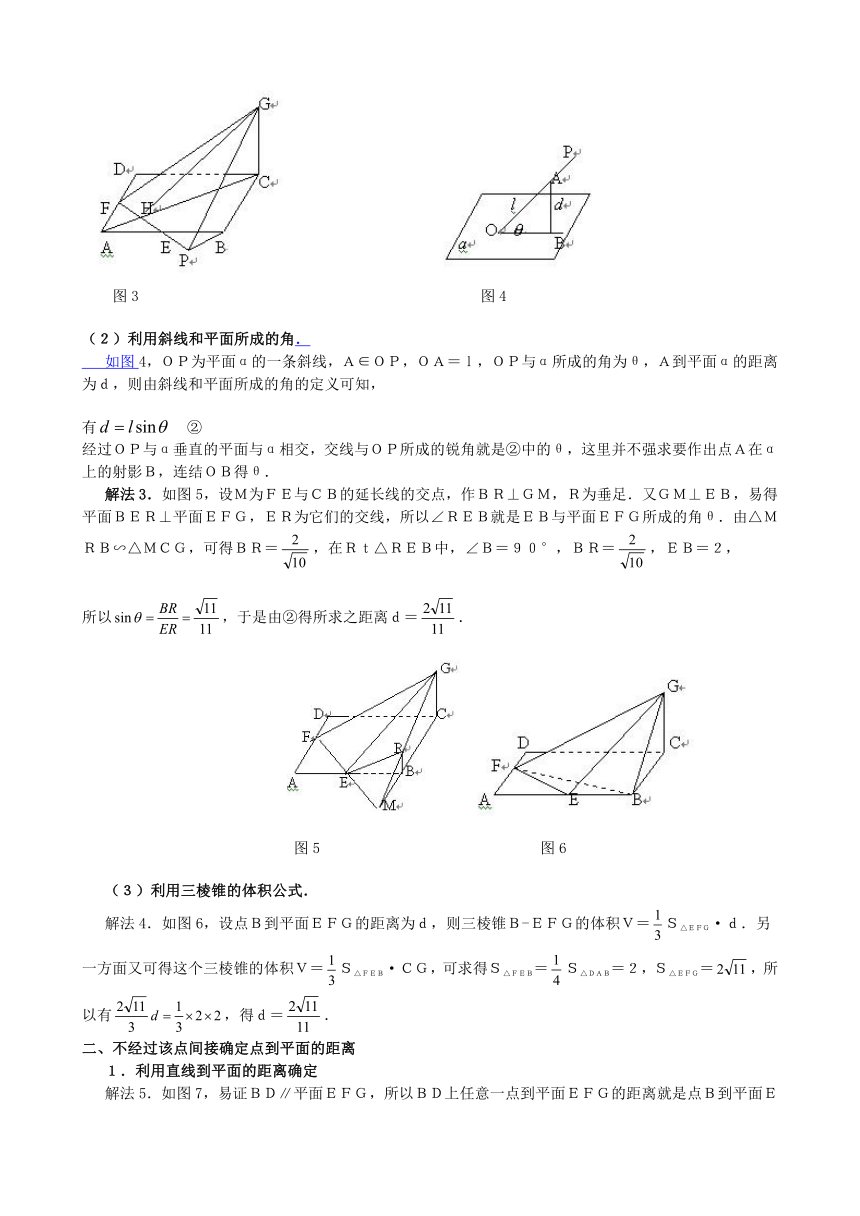
（２）利用斜线和平面所成的角．
　
如图
( http: / / www.21cnjy.com )4，ＯＰ为平面α的一条斜线，Ａ∈ＯＰ，ＯＡ＝ｌ，ＯＰ与α所成的角为θ，Ａ到平面α的距离为ｄ，则由斜线和平面所成的角的定义可知，
有
②
经过ＯＰ与α垂直的平面与α相交，交线与ＯＰ所成的锐角就是②中的θ，这里并不强求要作出点Ａ在α上的射影Ｂ，连结ＯＢ得θ．
　
解法3．如图5，设Ｍ为ＦＥ与ＣＢ的延长线的交点，作ＢＲ⊥ＧＭ，Ｒ为垂足．又ＧＭ⊥ＥＢ，易得平面ＢＥＲ⊥平面ＥＦＧ，ＥＲ为它们的交线，所以∠ＲＥＢ就是ＥＢ与平面ＥＦＧ所成的角θ．由△ＭＲＢ∽△ＭＣＧ，可得ＢＲ＝，在Ｒｔ△ＲＥＢ中，∠Ｂ＝９０°，ＢＲ＝，ＥＢ＝２，
所以，于是由②得所求之距离ｄ＝．
　　　　　　　　
INCLUDEPICTURE
"http://www.cbe21.com/subject/maths/images/040601/2016/2016015.gif"
\
MERGEFORMATINET
INCLUDEPICTURE
"http://www.cbe21.com/subject/maths/images/040601/2016/2016016.gif"
\
MERGEFORMATINET
图5　　　　　　　　　　　　　　
图6
　
（３）利用三棱锥的体积公式．
　
解法4．如图6，设点Ｂ到平面ＥＦＧ的距离为ｄ，则三棱锥Ｂ-ＥＦＧ的体积Ｖ＝Ｓ△ＥＦＧ·ｄ．另一方面又可得这个三棱锥的体积Ｖ＝Ｓ△ＦＥＢ·ＣＧ，可求得Ｓ△ＦＥＢ＝Ｓ△ＤＡＢ＝２，Ｓ△ＥＦＧ＝，所以有，得ｄ＝．
二、不经过该点间接确定点到平面的距离
　
１．利用直线到平面的距离确定
　
解法5．如图7，易证ＢＤ∥平面ＥＦＧ，所以ＢＤ上任意一点到平面ＥＦＧ的距离就是点Ｂ到平面ＥＦＧ的距离．由对称思想可知，取ＢＤ中点Ｏ，求点Ｏ到平面ＥＦＧ的距离较简单．ＡＣ交ＥＦ于Ｈ，交ＢＤ于Ｏ．易证平面ＧＨＣ⊥平面ＥＦＧ，作ＯＫ⊥ＨＧ，Ｋ为垂足，ＯＫ＝为所求之距离．
INCLUDEPICTURE
"http://www.cbe21.com/subject/maths/images/040601/2016/2016018.gif"
\
MERGEFORMATINET
　　　　　　　
INCLUDEPICTURE
"http://www.cbe21.com/subject/maths/images/040601/2016/2016019.gif"
\
MERGEFORMATINET
图7　　　　　　　　　　　　　　　　　　　　图8
　
２．利用平行平面间的距离确定
　
如图
( http: / / www.21cnjy.com )8，把平面ＥＦＧ补成一个正四棱柱的截面所在的平面，可使题设中的点、线、面之间的位置关系更加明朗．面ＧＭＴ是正四棱柱ＡＢＣＤ-Ａ１Ｂ１ＧＤ１经过Ｆ、Ｅ、Ｇ的截面所在的平面．ＭＧ交ＢＢ１于Ｎ，ＴＧ交ＤＤ１于Ｑ，作ＢＰ∥ＭＧ，交ＣＧ于Ｐ，连结ＤＰ，则有平面ＧＴＭ∥平面ＰＤＢ．它们之间的距离就是所求之距离．于是可以把点Ｂ平移到平面ＰＤＢ上任何一个位置，哪里方便就在哪里求．
　
这两个平行平面的距离ｄ又同三棱柱ＧＱＮ-ＰＤＢ的体积有关，所以也可以利用三棱柱的体积确定所求之距离．据此可得解法６．
　
解法6．三棱柱ＧＱＮ-ＰＤＢ的体积Ｖ＝Ｓ△ＰＤＢ·ｄ，另一方面又有
Ｖ＝Ｓ△ＣＤＢ·ＢＮ，可求得ＢＮ＝，ＣＰ＝，ＰＢ＝ＰＤ＝，ＢＤ＝，
Ｓ△ＰＤＢ＝，Ｓ△ＣＤＢ＝８，
所以·ｄ＝８·２/３，得ｄ＝为所求之距离．
三、利用坐标法确定点到平面的距离
利用空间两点间距离公式确定点到平面的距离
建立空间直角坐标系，过B做平面EFG的垂线
( http: / / www.21cnjy.com )，垂足为H，利用BH分别与EF、EG和GH垂直，利用两个向量垂直其数量积为零可解得H点的坐标，然后利用两点间距离公式可求点B到平面EFG的距离.
解法7
以C为原点，分别以
( http: / / www.21cnjy.com )CB、CD、CG所在直线为x轴、y轴和z轴建立空间直角坐标系(如图)，则C、B、E、F、G的坐标为C(0,0,0),B(4,0,0),E(4,2,0),
F((2,4,0),G(0,0,2)。故
设直线GH垂直平面EFG，垂足为H其坐标为H
(x,y,z)，则
，
解之得
故
所以点B到平面ＥＦＧ的距离
2.利用法向量确定点到平面的距离
建立空间直角坐标系，求出平面EFG的一个法向量，求线段BG在法向量上的射影长即为点B到平面ＥＦＧ的距离d.
解法8
以C为原点，分别以CB、CD
( http: / / www.21cnjy.com )、CG所在直线为x轴、y轴和z轴建立空间直角坐标系(如图)，则C、B、E、F、G的坐标为C(0,0,0),B(4,0,0),E(4,2,0),
F((2,4,0),G(0,0,2)。故
设平面EFG的法向量为
令x=1,则y=1,z=3,所以平面EFG的一个法向量为
设与平面EFG的法向量所成的角为θ，点B到平面ＥＦＧ的距离d,则
即点B到平面ＥＦＧ的距离.