北师大版九年级数学下册教学课件:2.2 二次函数的图象与性质(共17张PPT)
文档属性
| 名称 | 北师大版九年级数学下册教学课件:2.2 二次函数的图象与性质(共17张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 222.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-11-15 08:58:13 | ||
图片预览




文档简介
课件17张PPT。二次函数的图象与性质1.探索经历二次函数y=x2的图象的作法和性质的过程,获得利用图象研究函数性质的经验.
2.能够利用描点法作出y=x2的图象,并能根据图象认识和理解二次函数y=x2的性质.
3.能够作出二次函数y=-x2的图象,并能比较它与y=x2的图象的异同,初步建立二次函数表达式与图象间的联系. 1.二次函数的定义
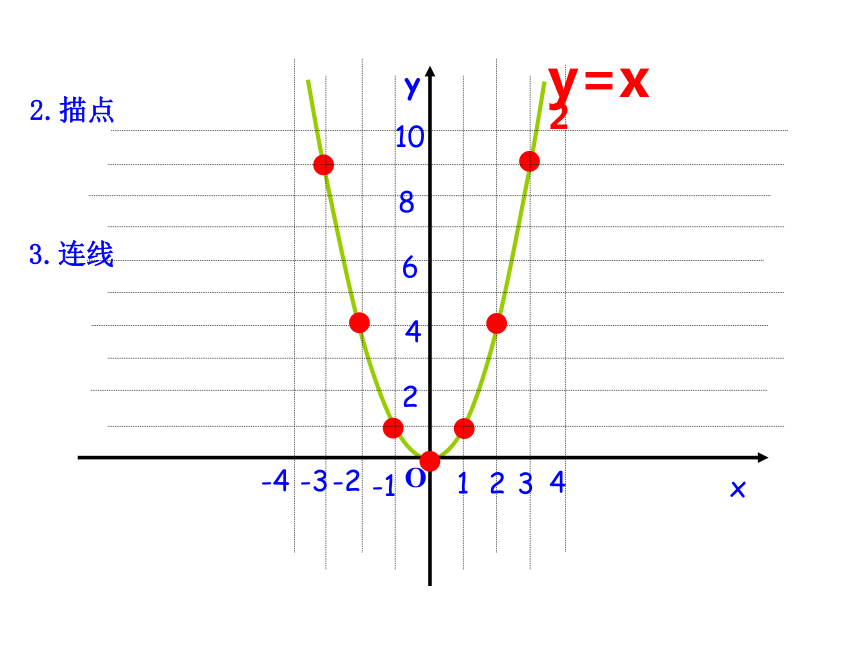
一般地,形如y=ax2+bx+c(a,b,c是常数,a≠0)的函数叫做x的二次函数.(1)列表.(3)连线.(2)描点.2.画函数图象的主要步骤是什么?请你画出二次函数 y=x2 的图象.1.列表:… -3 -2 -1 0 1 2 3 …… 9 4 1 0 1 4 9 … xyO-4-3-2-11234108642y=x22.描点3.连线议一议
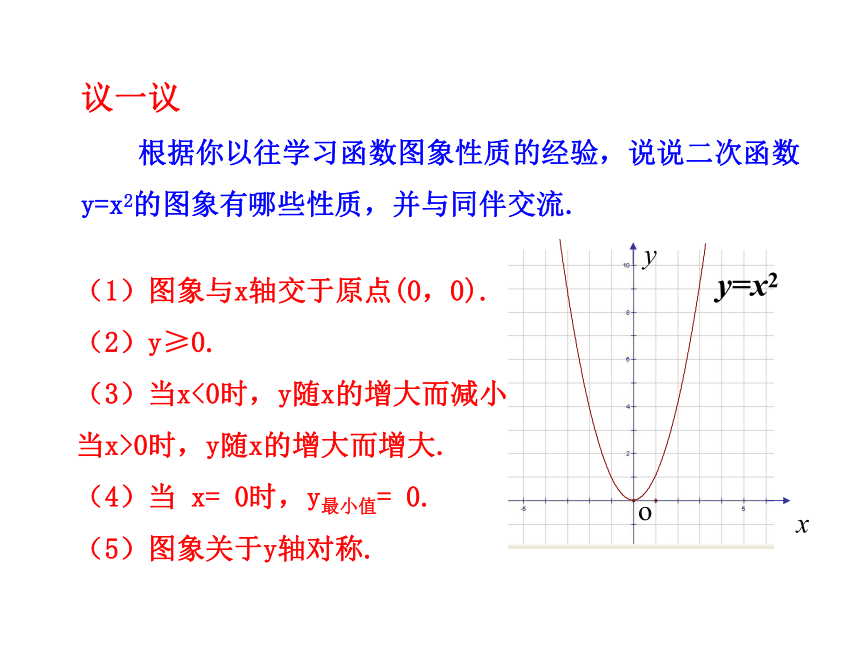
根据你以往学习函数图象性质的经验,说说二次函数y=x2的图象有哪些性质,并与同伴交流.(1)图象与x轴交于原点(0,0).
(2)y≥0.
(3)当x<0时,y随x的增大而减小,当x>0时,y随x的增大而增大.
(4)当 x= 0时,y最小值= 0.
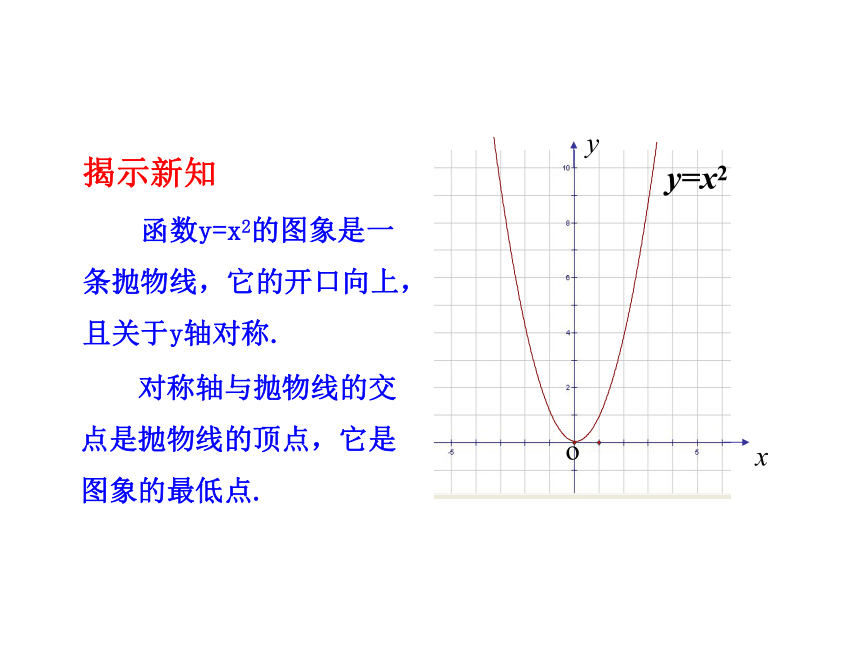
(5)图象关于y轴对称.xyoy=x2xyoy=x2 函数y=x2的图象是一条抛物线,它的开口向上,且关于y轴对称. 对称轴与抛物线的交点是抛物线的顶点,它是图象的最低点.揭示新知二次函数y=-x2的图象是什么形状?先想一想,然后作出它的图象,它与二次函数y=x2的图象有什么关系?与同伴进行交流.xyoy=x2 做一做说说二次函数y=-x2的图象
有哪些性质,与同伴交流.
(1)图象与x轴交于原点(0,0).
(2)y≤0.
(3)当x<0时,y随x的增大而增大;当x>0时,y随x的增大而减小.
(4)当x=0时,y最大值=0.
(5)图象关于y轴对称.oxyy=-x2 议一议1.抛物线y=2x2的顶点坐标是 ,对称轴是
.在 侧,y随着x的增大而增
大;在 侧,y随着x的增大而减小,当
x= 时,函数y的值最小,最小值是 ,抛
物线y=2x2在x轴的 方(除顶点外).2.抛物线 在x轴的 方(除顶点外),在对称轴的左侧,y随着x的 ;在对称轴的右侧,y随着x的 ,当x=0时,函数y的值最大,最大值是 ,当x 0时,y<0.(0,0)y轴对称轴的右对称轴的左00上下增大而增大增大而减小0【跟踪训练】【答案】选C.1.(盐城·中考)给出下列四个函数:;②;③;④①时y随x的增大而减小的函数有( )A.1 B.2个 C.3个 D.4个2.(盐城·中考)写出图象经过点(1,-1)的一个函数关系式 .【答案】y=x2-2x(答案不唯一)3.(烟台·中考)如图,AB为半圆的直径,点P为AB上一动点,动点P从点A出发,沿AB匀速运动到点B,运动时间为t,分别以AP与PB为直径作半圆,则图中阴影部分的面积S与时间t之间的函数图象大致为( )【答案】选D. tsAtsBtsCtsDOOOOA.(4,4) B.(1,-4)
C.(2,0) D.(0,4)4.(哈尔滨·中考)在抛物线上的一个点是( )【答案】选C. 1.函数y=ax2 (a≠0)的图象是一条抛物线,它的开口方向是由a的符号决定的,a<0开口向下,a>0开口向上,图象是关于y轴对称的轴对称图形.2.对称轴与抛物线的交点是抛物线的顶点,它是图象的最低(高)点.【规律方法】二次函数y=±x2的性质1.顶点坐标与对称轴.2.位置与开口方向.3.增减性与最值.o奋斗就是生活,人生只有前进。
——巴金
2.能够利用描点法作出y=x2的图象,并能根据图象认识和理解二次函数y=x2的性质.
3.能够作出二次函数y=-x2的图象,并能比较它与y=x2的图象的异同,初步建立二次函数表达式与图象间的联系. 1.二次函数的定义
一般地,形如y=ax2+bx+c(a,b,c是常数,a≠0)的函数叫做x的二次函数.(1)列表.(3)连线.(2)描点.2.画函数图象的主要步骤是什么?请你画出二次函数 y=x2 的图象.1.列表:… -3 -2 -1 0 1 2 3 …… 9 4 1 0 1 4 9 … xyO-4-3-2-11234108642y=x22.描点3.连线议一议
根据你以往学习函数图象性质的经验,说说二次函数y=x2的图象有哪些性质,并与同伴交流.(1)图象与x轴交于原点(0,0).
(2)y≥0.
(3)当x<0时,y随x的增大而减小,当x>0时,y随x的增大而增大.
(4)当 x= 0时,y最小值= 0.
(5)图象关于y轴对称.xyoy=x2xyoy=x2 函数y=x2的图象是一条抛物线,它的开口向上,且关于y轴对称. 对称轴与抛物线的交点是抛物线的顶点,它是图象的最低点.揭示新知二次函数y=-x2的图象是什么形状?先想一想,然后作出它的图象,它与二次函数y=x2的图象有什么关系?与同伴进行交流.xyoy=x2 做一做说说二次函数y=-x2的图象
有哪些性质,与同伴交流.
(1)图象与x轴交于原点(0,0).
(2)y≤0.
(3)当x<0时,y随x的增大而增大;当x>0时,y随x的增大而减小.
(4)当x=0时,y最大值=0.
(5)图象关于y轴对称.oxyy=-x2 议一议1.抛物线y=2x2的顶点坐标是 ,对称轴是
.在 侧,y随着x的增大而增
大;在 侧,y随着x的增大而减小,当
x= 时,函数y的值最小,最小值是 ,抛
物线y=2x2在x轴的 方(除顶点外).2.抛物线 在x轴的 方(除顶点外),在对称轴的左侧,y随着x的 ;在对称轴的右侧,y随着x的 ,当x=0时,函数y的值最大,最大值是 ,当x 0时,y<0.(0,0)y轴对称轴的右对称轴的左00上下增大而增大增大而减小0【跟踪训练】【答案】选C.1.(盐城·中考)给出下列四个函数:;②;③;④①时y随x的增大而减小的函数有( )A.1 B.2个 C.3个 D.4个2.(盐城·中考)写出图象经过点(1,-1)的一个函数关系式 .【答案】y=x2-2x(答案不唯一)3.(烟台·中考)如图,AB为半圆的直径,点P为AB上一动点,动点P从点A出发,沿AB匀速运动到点B,运动时间为t,分别以AP与PB为直径作半圆,则图中阴影部分的面积S与时间t之间的函数图象大致为( )【答案】选D. tsAtsBtsCtsDOOOOA.(4,4) B.(1,-4)
C.(2,0) D.(0,4)4.(哈尔滨·中考)在抛物线上的一个点是( )【答案】选C. 1.函数y=ax2 (a≠0)的图象是一条抛物线,它的开口方向是由a的符号决定的,a<0开口向下,a>0开口向上,图象是关于y轴对称的轴对称图形.2.对称轴与抛物线的交点是抛物线的顶点,它是图象的最低(高)点.【规律方法】二次函数y=±x2的性质1.顶点坐标与对称轴.2.位置与开口方向.3.增减性与最值.o奋斗就是生活,人生只有前进。
——巴金
