人教b版必修1数学:第2章函数-高效综合
文档属性
| 名称 | 人教b版必修1数学:第2章函数-高效综合 |  | |
| 格式 | rar | ||
| 文件大小 | 809.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2010-09-25 19:29:00 | ||
图片预览






文档简介
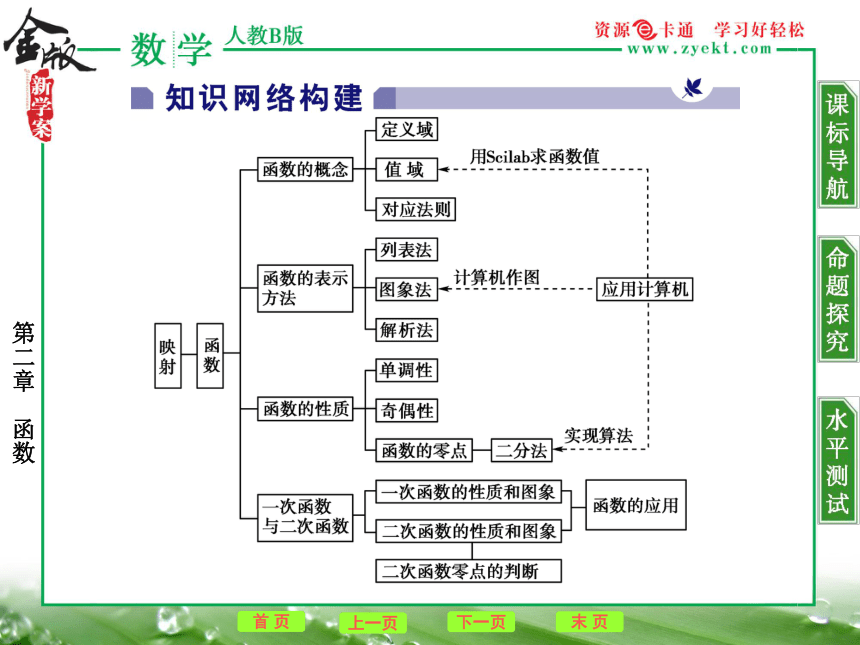
课件18张PPT。1.函数的概念与表示方法
(1)会用集合与对应语言来刻画函数,了解构成函数的三要素,了解映射的概念.
(2)会用区间表示数集,会求简单函数的定义域和值域.
(3)会根据不同需要选择恰当的方法表示函数,了解简单的分段函数并能简单应用.
2.函数的性质
(1)理解函数的单调性及几何意义,了解函数奇偶性的意义.
(2)学会运用函数图象理解和研究函数的性质.3.一次函数和二次函数
(1)掌握一次函数和二次函数的性质.
(2)掌握配方法和待定系数法.
(3)了解一次函数模型、二次函数模型、分段函数模型的广泛应用;能解决一些简单的实际问题.
4.函数与方程
(1)了解函数的零点与方程根的联系.
(2)能借助计算器用二分法求函数的近似零点,即方程的近似解. 1.函数的概念与表示方法
(1)求定义域、值域、解析式和函数值等问题一直是高考的重点,很多时候会与其他知识结合考查.(2)函数的表示方法是高考考查的热点,以选择题或填空题的形式居多,主要考查数学语言(表格、图象、符号、)识图和用图的能力;分段函数知识,在高考中也比较多见.
2.函数的性质
(1)函数的单调性是函数的重要性质之一,是今后研究具体函数的单调性的理论基础.因此,函数的单调性一直是高考考查的重点之一,在选择题、填空题中,主要考查函数的单调性和最值概念,题目特点是小、巧、活.解答题中常涉及到函数的单调性和最值问题的代数推理题,综合性强、难度大.
(2)函数的奇偶性是高考的必考内容,从考查形式看:一方面考查函数奇偶性定义的应用,属于试卷中的容易题;另一方面综合考查函数的性质(单调性、奇偶性等),一般属于试卷中的中档题.
3.一次函数和二次函数
(1)一次函数常作为分段函数的一段在高考题中出现.
(2)二次函数是研究函数的单调性、最值等性质的良好素材,是最重要的函数应用模型之一.高考考查的热点是二次函数的解析式、单调性、最值、图象、应用等.在选择题、填空题和解答题中均有涉及.几乎与高中阶段所有数学知识都可以联系和综合起来进行考查.
4.函数与方程
函数与方程思想是最重要的一种数学思想,高考中所占比重较大,综合知识多、题型多、应用技巧多.近几年高考中,多见于求变量的取值范围,解方程等. 已知不等式1≤-x2+x+a+1≤ 对一切x∈[-1,1]恒成立,求a的取值范围.1.用函数的值域(最值)解题
求函数的值域(或最值),涉及到众多的数学知识,构成了中学数学的重要横向知识体系,同时也为利用函数值域解题提供了广阔天地.尤其对某些含参数的不等式或方程,在分离参数的基础上,通过求函数的值域进而确定参数的取值范围,从而避免了对参数的繁琐讨论. 作出函数y=G(x)=x|x-2|,x∈R的图象,利用图象分别求G(x)=1,G(x)≥1的解集.2.利用函数图象解题
函数的图象是函数关系的形象体现,它能直观地反映出函数的性质,因此利用图象可以研究函数的性质及解决其他问题.
【解析】 G(x)=x|x-2|利用描点法作出图象,如右图所示.
在图象上作出y=1.
可知:当x=1,或x=1+ 时,G(x)=1;
当x≥1+ 时,G(x)≥1.
∴G(x)=1的解集为{x|x=1,或x=1+ },
G(x)≥1的解集为{x|x≥1+ ,或x=1}.3.运用函数的单调性解题
单调性是函数的重要性质,某些数学问题,通过单调性,可将函数值间的关系转化为自变量间的关系进行研究,从而达到化繁为简的目的.特别是在比较大小,证明不等式,求值或求最值,解方程(组)等方面应用十分广泛. (1)定义在[-2,2]上的偶函数f(x),当x≥0时单调递减,设f(1-m)<f(m),求m的取值范围;
(2)解不等式(x2-20x+38)3+4x2+152<x3+84x.
【解析】 (1)∵f(1-m)<f(m),f(x)是偶函数,
∴f(|1-m|)=f(1-m),f(|m|)=f(m).
∴f(|1-m|)<f(|m|).
又当x≥0时单调递减,于是可化为(2)原不等式可变形为(x2-20x+38)3+4(x2-20x+38)<x3+4x,
令f(x)=x3+4x,则原不等式即为
f(x2-20x+38)<f(x).
∵f(x)=x3+4x在R上是增函数,
∴x2-20x+38<x,即x2-21x+38<0.
即(x-2)(x-19)<0,解得2<x<19.
4.利用待定系数法解题
使用待定系数法,就是把具有某种确定形式的数学问题,通过引入一些待定的系数,转化为x的方程式或方程组来解.待定系数法在求函数解析式中有着极为广泛的应用. 已知二次函数y=f(x)的最大值等于13,且f(3)=f(-1)=5,求f(x)的解析式.
【解析】 ∵f(3)=f(-1),
∴拋物线y=f(x)有对称轴x=1.
又y=f(x)的最大值是13,
故可设f(x)=a(x-1)2+13.
将点(3,5)代入,求得a=-2,
∴f(x)=-2(x-1)2+13=-2x2+4x+11.31.用函数与方程的思想解题函数f(x)=x4-15,下列结论正确的有哪几个? ①f(x)=0在[1,2]内有一实根;
②f(x)=0在[-2,-1]内有一实根;
③f(x)=0没有大于2的实根;
④f(x)=0没有小于-2的实根;
⑤f(x)=0有四个实数根.
【解析】 f(x)=x4-15是偶函数,并且x>0时,f(x)是增函数,x<0时,f(x)是减函数.
∵f(1)=-14<0,f(2)=1>0,
∴f(x)=0在[1,2]内有一个实根,同时,在[-2,-1]内也有一个实根,且f(x)=0只有这两个实根,所以①②正确,⑤不正确.
∵f(2)>0,且当x>2时f(x)>f(2)>0,
∴f(x)=0没有大于2的实根.同理f(x)=0没有小于-2的实根,所以③④也正确.
综上可知,①②③④正确,⑤不正确.2.用数形结合的思想解题 设f(x)表示y=-x+6和y=-2x2+4x+6中较小者,求函数f(x)的最大值.
【解析】 在同一坐标系中分别作出函数y=-x+6和y=-2x2+4x+6的图象,图中的实线部分为函数y=f(x)的图象.由-x+6=-2x2+4x+6得
x1=0,x2= ,
由图易知当x=0时,f(x)有最大值为6.
3.用分类讨论的思想解题设f(x)=x2-4x-4,x∈[t,t+1](t∈R),求函数f(x)的最小值g(t)的解析式.
【解析】 ∵f(x)=(x-2)2-8,x∈[t,t+1],
∴当2∈[t,t+1]时,即t≤2≤t+1时,g(t)=f(2)=-8.
当t+1<2,即t<1时,f(x)在[t,t+1]上是减函数.
∴g(t)=f(t+1)=t2-2t-7;
当t>2时,f(x)在[t,t+1]上是增函数,
∴g(t)=f(t)=t2-4t-4.对于满足|p|≤2的所有实数p,求使不等式x2+px+1>p+2x恒成立的x的取值范围.
【解析】 原不等式可变形为(x-1)p+x2-2x+1>0,
设f(p)=(x-1)p+x2-2x+1,
则f(p)在[-2,2]上恒大于0,故有
∴x<-1,或x>3.4.用等价转化的思想解题课时作业
点击进入链接
(1)会用集合与对应语言来刻画函数,了解构成函数的三要素,了解映射的概念.
(2)会用区间表示数集,会求简单函数的定义域和值域.
(3)会根据不同需要选择恰当的方法表示函数,了解简单的分段函数并能简单应用.
2.函数的性质
(1)理解函数的单调性及几何意义,了解函数奇偶性的意义.
(2)学会运用函数图象理解和研究函数的性质.3.一次函数和二次函数
(1)掌握一次函数和二次函数的性质.
(2)掌握配方法和待定系数法.
(3)了解一次函数模型、二次函数模型、分段函数模型的广泛应用;能解决一些简单的实际问题.
4.函数与方程
(1)了解函数的零点与方程根的联系.
(2)能借助计算器用二分法求函数的近似零点,即方程的近似解. 1.函数的概念与表示方法
(1)求定义域、值域、解析式和函数值等问题一直是高考的重点,很多时候会与其他知识结合考查.(2)函数的表示方法是高考考查的热点,以选择题或填空题的形式居多,主要考查数学语言(表格、图象、符号、)识图和用图的能力;分段函数知识,在高考中也比较多见.
2.函数的性质
(1)函数的单调性是函数的重要性质之一,是今后研究具体函数的单调性的理论基础.因此,函数的单调性一直是高考考查的重点之一,在选择题、填空题中,主要考查函数的单调性和最值概念,题目特点是小、巧、活.解答题中常涉及到函数的单调性和最值问题的代数推理题,综合性强、难度大.
(2)函数的奇偶性是高考的必考内容,从考查形式看:一方面考查函数奇偶性定义的应用,属于试卷中的容易题;另一方面综合考查函数的性质(单调性、奇偶性等),一般属于试卷中的中档题.
3.一次函数和二次函数
(1)一次函数常作为分段函数的一段在高考题中出现.
(2)二次函数是研究函数的单调性、最值等性质的良好素材,是最重要的函数应用模型之一.高考考查的热点是二次函数的解析式、单调性、最值、图象、应用等.在选择题、填空题和解答题中均有涉及.几乎与高中阶段所有数学知识都可以联系和综合起来进行考查.
4.函数与方程
函数与方程思想是最重要的一种数学思想,高考中所占比重较大,综合知识多、题型多、应用技巧多.近几年高考中,多见于求变量的取值范围,解方程等. 已知不等式1≤-x2+x+a+1≤ 对一切x∈[-1,1]恒成立,求a的取值范围.1.用函数的值域(最值)解题
求函数的值域(或最值),涉及到众多的数学知识,构成了中学数学的重要横向知识体系,同时也为利用函数值域解题提供了广阔天地.尤其对某些含参数的不等式或方程,在分离参数的基础上,通过求函数的值域进而确定参数的取值范围,从而避免了对参数的繁琐讨论. 作出函数y=G(x)=x|x-2|,x∈R的图象,利用图象分别求G(x)=1,G(x)≥1的解集.2.利用函数图象解题
函数的图象是函数关系的形象体现,它能直观地反映出函数的性质,因此利用图象可以研究函数的性质及解决其他问题.
【解析】 G(x)=x|x-2|利用描点法作出图象,如右图所示.
在图象上作出y=1.
可知:当x=1,或x=1+ 时,G(x)=1;
当x≥1+ 时,G(x)≥1.
∴G(x)=1的解集为{x|x=1,或x=1+ },
G(x)≥1的解集为{x|x≥1+ ,或x=1}.3.运用函数的单调性解题
单调性是函数的重要性质,某些数学问题,通过单调性,可将函数值间的关系转化为自变量间的关系进行研究,从而达到化繁为简的目的.特别是在比较大小,证明不等式,求值或求最值,解方程(组)等方面应用十分广泛. (1)定义在[-2,2]上的偶函数f(x),当x≥0时单调递减,设f(1-m)<f(m),求m的取值范围;
(2)解不等式(x2-20x+38)3+4x2+152<x3+84x.
【解析】 (1)∵f(1-m)<f(m),f(x)是偶函数,
∴f(|1-m|)=f(1-m),f(|m|)=f(m).
∴f(|1-m|)<f(|m|).
又当x≥0时单调递减,于是可化为(2)原不等式可变形为(x2-20x+38)3+4(x2-20x+38)<x3+4x,
令f(x)=x3+4x,则原不等式即为
f(x2-20x+38)<f(x).
∵f(x)=x3+4x在R上是增函数,
∴x2-20x+38<x,即x2-21x+38<0.
即(x-2)(x-19)<0,解得2<x<19.
4.利用待定系数法解题
使用待定系数法,就是把具有某种确定形式的数学问题,通过引入一些待定的系数,转化为x的方程式或方程组来解.待定系数法在求函数解析式中有着极为广泛的应用. 已知二次函数y=f(x)的最大值等于13,且f(3)=f(-1)=5,求f(x)的解析式.
【解析】 ∵f(3)=f(-1),
∴拋物线y=f(x)有对称轴x=1.
又y=f(x)的最大值是13,
故可设f(x)=a(x-1)2+13.
将点(3,5)代入,求得a=-2,
∴f(x)=-2(x-1)2+13=-2x2+4x+11.31.用函数与方程的思想解题函数f(x)=x4-15,下列结论正确的有哪几个? ①f(x)=0在[1,2]内有一实根;
②f(x)=0在[-2,-1]内有一实根;
③f(x)=0没有大于2的实根;
④f(x)=0没有小于-2的实根;
⑤f(x)=0有四个实数根.
【解析】 f(x)=x4-15是偶函数,并且x>0时,f(x)是增函数,x<0时,f(x)是减函数.
∵f(1)=-14<0,f(2)=1>0,
∴f(x)=0在[1,2]内有一个实根,同时,在[-2,-1]内也有一个实根,且f(x)=0只有这两个实根,所以①②正确,⑤不正确.
∵f(2)>0,且当x>2时f(x)>f(2)>0,
∴f(x)=0没有大于2的实根.同理f(x)=0没有小于-2的实根,所以③④也正确.
综上可知,①②③④正确,⑤不正确.2.用数形结合的思想解题 设f(x)表示y=-x+6和y=-2x2+4x+6中较小者,求函数f(x)的最大值.
【解析】 在同一坐标系中分别作出函数y=-x+6和y=-2x2+4x+6的图象,图中的实线部分为函数y=f(x)的图象.由-x+6=-2x2+4x+6得
x1=0,x2= ,
由图易知当x=0时,f(x)有最大值为6.
3.用分类讨论的思想解题设f(x)=x2-4x-4,x∈[t,t+1](t∈R),求函数f(x)的最小值g(t)的解析式.
【解析】 ∵f(x)=(x-2)2-8,x∈[t,t+1],
∴当2∈[t,t+1]时,即t≤2≤t+1时,g(t)=f(2)=-8.
当t+1<2,即t<1时,f(x)在[t,t+1]上是减函数.
∴g(t)=f(t+1)=t2-2t-7;
当t>2时,f(x)在[t,t+1]上是增函数,
∴g(t)=f(t)=t2-4t-4.对于满足|p|≤2的所有实数p,求使不等式x2+px+1>p+2x恒成立的x的取值范围.
【解析】 原不等式可变形为(x-1)p+x2-2x+1>0,
设f(p)=(x-1)p+x2-2x+1,
则f(p)在[-2,2]上恒大于0,故有
∴x<-1,或x>3.4.用等价转化的思想解题课时作业
点击进入链接
