第六章 第一节 平行四边形的性质 课时2同步练习
文档属性
| 名称 | 第六章 第一节 平行四边形的性质 课时2同步练习 |  | |
| 格式 | zip | ||
| 文件大小 | 455.4KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-02-17 07:06:35 | ||
图片预览

文档简介
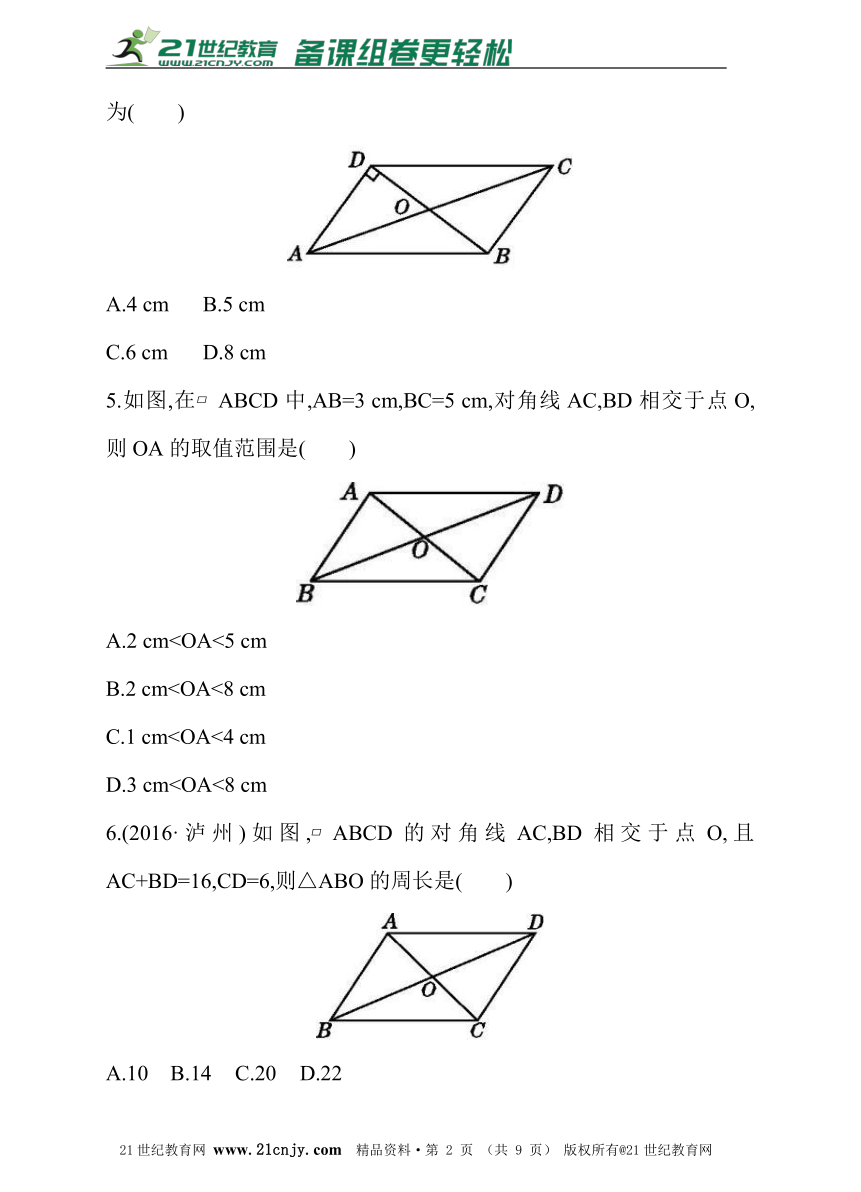
第一节 平行四边形的性质
第2课时 平行四边形的对角线性质
基础检测
知识点1平行四边形的对角线互相平分
1.平行四边形的对角线_________,并将四边形分成_________对全等三角形, _________个面积相等的三角形.?21教育网
2.如图,?ABCD的对角线AC,BD相交于点O,则下列说法一定正确的是( )
A.AO=OD B.AO⊥OD
C.AO=OC D.AO⊥AB
3.(2016·丽水)如图,?ABCD的对角线AC,BD交于点O,已知AD=8,BD=12,AC=6,则△OBC的周长为( )21cnjy.com
A.13 B.17
C.20 D.26
4.如图,在?ABCD中,已知∠ODA=90°,AC=10 cm,BD=6 cm,则AD的长为( )www.21-cn-jy.com
A.4 cm B.5 cm
C.6 cm D.8 cm
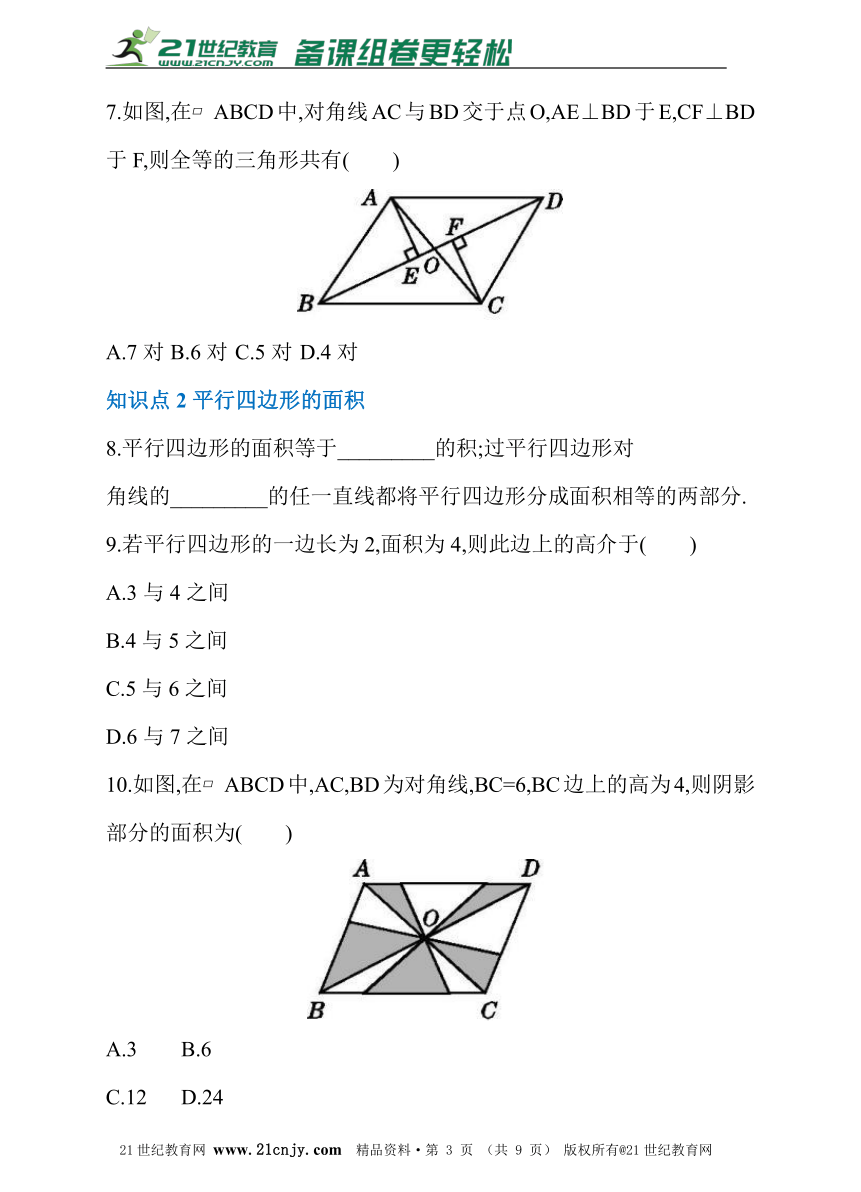
5.如图,在?ABCD中,AB=3 cm,BC=5 cm,对角线AC,BD相交于点O,则OA的取值范围是( )2·1·c·n·j·y
A.2 cmB.2 cmC.1 cmD.3 cm6.(2016·泸州)如图,?ABCD的对角线AC,BD相交于点O,且AC+BD=16,CD=6,则△ABO的周长是( )21·世纪*教育网
A.10 B.14 C.20 D.22
7.如图,在?ABCD中,对角线AC与BD交于点O,AE⊥BD于E,CF⊥BD于F,则全等的三角形共有( )www-2-1-cnjy-com
A.7对 B.6对 C.5对 D.4对
知识点2平行四边形的面积
8.平行四边形的面积等于_________的积;过平行四边形对
角线的_________的任一直线都将平行四边形分成面积相等的两部分.?
9.若平行四边形的一边长为2,面积为4,则此边上的高介于( )
A.3与4之间
B.4与5之间
C.5与6之间
D.6与7之间
10.如图,在?ABCD中,AC,BD为对角线,BC=6,BC边上的高为4,则阴影部分的面积为( ) 21世纪教育网版权所有
A.3 B.6
C.12 D.24
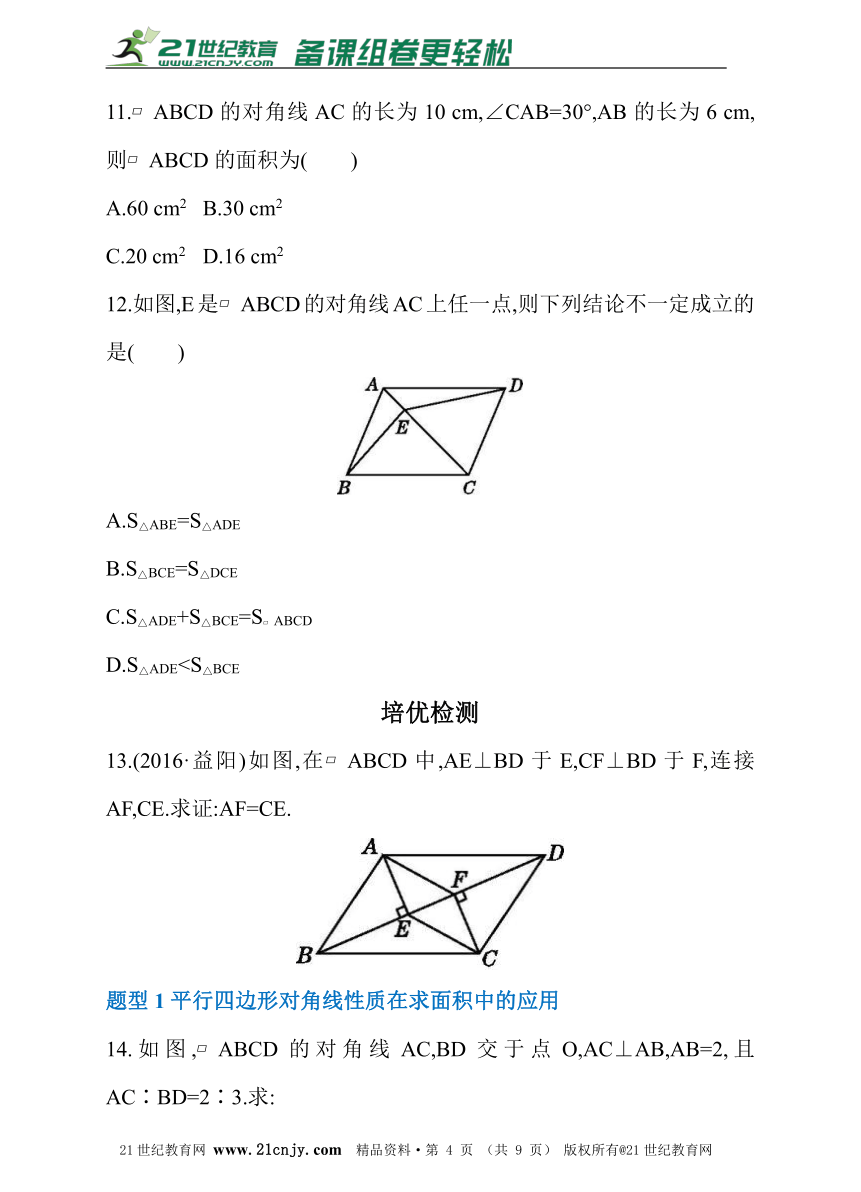
11.?ABCD的对角线AC的长为10 cm,∠CAB=30°,AB的长为6 cm,则?ABCD的面积为( )【来源:21·世纪·教育·网】
A.60 cm2 B.30 cm2
C.20 cm2 D.16 cm2
12.如图,E是?ABCD的对角线AC上任一点,则下列结论不一定成立的是( )
A.S△ABE=S△ADE
B.S△BCE=S△DCE
C.S△ADE+S△BCE=S?ABCD
D.S△ADE培优检测
13.(2016·益阳)如图,在?ABCD中,AE⊥BD于E,CF⊥BD于F,连接AF,CE.求证:AF=CE.21·cn·jy·com
题型1平行四边形对角线性质在求面积中的应用
14.如图,?ABCD的对角线AC,BD交于点O,AC⊥AB,AB=2,且AC∶BD=2∶3.求:
(1)AC的长;
(2)△AOD的面积.
题型2平行四边形对角线性质在坐标系中的应用
15.如图,已知点A(-4,2),B(-1,-2),?ABCD的对角线交于坐标原点O.
(1)请直接写出点C,D的坐标;
(2)写出从线段AB到线段CD的变换过程;
(3)直接写出?ABCD的面积.
题型3平行四边形对角线性质在判断线段关系 中的应用
16.如图①,?ABCD的对角线AC,BD相交于点O,EF过点O且与AD,BC分别相交于点E,F,则OE=OF.若EF过点O且与平行四边形的两对边的延长线分别相交于点E,F(图②和图③),OE与OF还相等吗?若相等,请说明理由.2-1-c-n-j-y
17.探究:如图①,在?ABCD中,AC,BD交于点O,过点O的直线交AD于E,交BC于F.
(1)求证:OE=OF.
(2)求证:四边形AEFB与四边形DEFC的周长相等;
(3)直线EF是否将?ABCD的面积二等分?
应用:张大爷家有一块平行四边形的菜园,园中有一口水井P,如图②所示,张大爷计划把菜园平均分成两块,分别种植西红柿和茄子,且使两块地共用这口水井,请你帮助张大爷把地分开.21*cnjy*com
参考答案
1.【答案】互相平分;2;4
2.【答案】C 3.【答案】B 4.【答案】A
5.【答案】C
6.【答案】B
7.【答案】A
8.【答案】底和高;交点
9.【答案】B 10.【答案】C 11.【答案】B
12.【答案】D
13.证明:∵四边形ABCD是平行四边形,
∴AB=CD,AB∥CD.∴∠ABE=∠CDF.
∵AE⊥BD,CF⊥BD,∴∠AEB=∠CFD=90°.
在△ABE和△CDF中,
∴△ABE≌△CDF(AAS).∴BE=DF.
连接AC,交BD于O,由平行四边形的对角线互相平分可得
OB=OD,OA=OC.∴OB-BE=OD-DF,即OE=OF.
在△AOF和△COE中,
∴△AOF≌△COE(SAS).∴AF=CE.
14.解:(1)∵AC∶BD=2∶3,∴设AC=2x,则BD=3x.
∵四边形ABCD是平行四边形,
∴OA=AC=x,OB=BD=x.
由OA2+AB2=OB2,得x2+22=,
解得x= (x=- 舍去),∴AC= .
(2)∵S?ABCD=AB·AC=2× = ,
∴S△AOD=S?ABCD= .
15.解:(1)C(4,-2),D(1,2).
(2)AB沿x轴向右平移5个单位长度到CD的位置(答案不唯一).
(3)S?ABCD=20.
16.解:图②中仍然相等.理由如下:
∵在?ABCD中,AB∥CD,OA=OC,∴∠E=∠F.
又∵∠AOE=∠COF,∴△AOE≌△COF(AAS).
∴OE=OF.
图③中仍然相等.理由如下:
∵在?ABCD中,AD∥BC,OA=OC,∴∠E=∠F.
又∵∠AOE=∠COF,∴△AOE≌△COF.
∴OE=OF.
17.(1)证明:∵在?ABCD中,AD∥BC,OB=OD,
∴∠OBF=∠ODE.
又∵∠BOF=∠DOE,
∴△BOF≌△DOE.
∴OE=OF.
(2)证明:由(1)知△BOF≌△DOE,
∴BF=DE.
∵在?ABCD中,AD∥BC,OA=OC,
∴∠OAE=∠OCF.
又∵∠AOE=∠COF,
∴△AOE≌△COF.
∴AE=CF.
又∵在?ABCD中,AB=CD,
四边形AEFB的周长=AE+EF+BF+AB,
四边形DEFC的周长=CF+EF+DE+CD,
∴四边形AEFB与四边形DEFC的周长相等.
(3)解:由(1)(2)可知△BOF≌△DOE,△COF≌△AOE.
又易证△AOB≌△COD,∴S四边形AEFB=S四边形DEFC.
即直线EF将?ABCD的面积二等分.
应用:连接AC,BD交于点O,作直线OP,则直线OP两旁的四边形面积相等(图略).
第2课时 平行四边形的对角线性质
基础检测
知识点1平行四边形的对角线互相平分
1.平行四边形的对角线_________,并将四边形分成_________对全等三角形, _________个面积相等的三角形.?21教育网
2.如图,?ABCD的对角线AC,BD相交于点O,则下列说法一定正确的是( )
A.AO=OD B.AO⊥OD
C.AO=OC D.AO⊥AB
3.(2016·丽水)如图,?ABCD的对角线AC,BD交于点O,已知AD=8,BD=12,AC=6,则△OBC的周长为( )21cnjy.com
A.13 B.17
C.20 D.26
4.如图,在?ABCD中,已知∠ODA=90°,AC=10 cm,BD=6 cm,则AD的长为( )www.21-cn-jy.com
A.4 cm B.5 cm
C.6 cm D.8 cm
5.如图,在?ABCD中,AB=3 cm,BC=5 cm,对角线AC,BD相交于点O,则OA的取值范围是( )2·1·c·n·j·y
A.2 cm
A.10 B.14 C.20 D.22
7.如图,在?ABCD中,对角线AC与BD交于点O,AE⊥BD于E,CF⊥BD于F,则全等的三角形共有( )www-2-1-cnjy-com
A.7对 B.6对 C.5对 D.4对
知识点2平行四边形的面积
8.平行四边形的面积等于_________的积;过平行四边形对
角线的_________的任一直线都将平行四边形分成面积相等的两部分.?
9.若平行四边形的一边长为2,面积为4,则此边上的高介于( )
A.3与4之间
B.4与5之间
C.5与6之间
D.6与7之间
10.如图,在?ABCD中,AC,BD为对角线,BC=6,BC边上的高为4,则阴影部分的面积为( ) 21世纪教育网版权所有
A.3 B.6
C.12 D.24
11.?ABCD的对角线AC的长为10 cm,∠CAB=30°,AB的长为6 cm,则?ABCD的面积为( )【来源:21·世纪·教育·网】
A.60 cm2 B.30 cm2
C.20 cm2 D.16 cm2
12.如图,E是?ABCD的对角线AC上任一点,则下列结论不一定成立的是( )
A.S△ABE=S△ADE
B.S△BCE=S△DCE
C.S△ADE+S△BCE=S?ABCD
D.S△ADE
13.(2016·益阳)如图,在?ABCD中,AE⊥BD于E,CF⊥BD于F,连接AF,CE.求证:AF=CE.21·cn·jy·com
题型1平行四边形对角线性质在求面积中的应用
14.如图,?ABCD的对角线AC,BD交于点O,AC⊥AB,AB=2,且AC∶BD=2∶3.求:
(1)AC的长;
(2)△AOD的面积.
题型2平行四边形对角线性质在坐标系中的应用
15.如图,已知点A(-4,2),B(-1,-2),?ABCD的对角线交于坐标原点O.
(1)请直接写出点C,D的坐标;
(2)写出从线段AB到线段CD的变换过程;
(3)直接写出?ABCD的面积.
题型3平行四边形对角线性质在判断线段关系 中的应用
16.如图①,?ABCD的对角线AC,BD相交于点O,EF过点O且与AD,BC分别相交于点E,F,则OE=OF.若EF过点O且与平行四边形的两对边的延长线分别相交于点E,F(图②和图③),OE与OF还相等吗?若相等,请说明理由.2-1-c-n-j-y
17.探究:如图①,在?ABCD中,AC,BD交于点O,过点O的直线交AD于E,交BC于F.
(1)求证:OE=OF.
(2)求证:四边形AEFB与四边形DEFC的周长相等;
(3)直线EF是否将?ABCD的面积二等分?
应用:张大爷家有一块平行四边形的菜园,园中有一口水井P,如图②所示,张大爷计划把菜园平均分成两块,分别种植西红柿和茄子,且使两块地共用这口水井,请你帮助张大爷把地分开.21*cnjy*com
参考答案
1.【答案】互相平分;2;4
2.【答案】C 3.【答案】B 4.【答案】A
5.【答案】C
6.【答案】B
7.【答案】A
8.【答案】底和高;交点
9.【答案】B 10.【答案】C 11.【答案】B
12.【答案】D
13.证明:∵四边形ABCD是平行四边形,
∴AB=CD,AB∥CD.∴∠ABE=∠CDF.
∵AE⊥BD,CF⊥BD,∴∠AEB=∠CFD=90°.
在△ABE和△CDF中,
∴△ABE≌△CDF(AAS).∴BE=DF.
连接AC,交BD于O,由平行四边形的对角线互相平分可得
OB=OD,OA=OC.∴OB-BE=OD-DF,即OE=OF.
在△AOF和△COE中,
∴△AOF≌△COE(SAS).∴AF=CE.
14.解:(1)∵AC∶BD=2∶3,∴设AC=2x,则BD=3x.
∵四边形ABCD是平行四边形,
∴OA=AC=x,OB=BD=x.
由OA2+AB2=OB2,得x2+22=,
解得x= (x=- 舍去),∴AC= .
(2)∵S?ABCD=AB·AC=2× = ,
∴S△AOD=S?ABCD= .
15.解:(1)C(4,-2),D(1,2).
(2)AB沿x轴向右平移5个单位长度到CD的位置(答案不唯一).
(3)S?ABCD=20.
16.解:图②中仍然相等.理由如下:
∵在?ABCD中,AB∥CD,OA=OC,∴∠E=∠F.
又∵∠AOE=∠COF,∴△AOE≌△COF(AAS).
∴OE=OF.
图③中仍然相等.理由如下:
∵在?ABCD中,AD∥BC,OA=OC,∴∠E=∠F.
又∵∠AOE=∠COF,∴△AOE≌△COF.
∴OE=OF.
17.(1)证明:∵在?ABCD中,AD∥BC,OB=OD,
∴∠OBF=∠ODE.
又∵∠BOF=∠DOE,
∴△BOF≌△DOE.
∴OE=OF.
(2)证明:由(1)知△BOF≌△DOE,
∴BF=DE.
∵在?ABCD中,AD∥BC,OA=OC,
∴∠OAE=∠OCF.
又∵∠AOE=∠COF,
∴△AOE≌△COF.
∴AE=CF.
又∵在?ABCD中,AB=CD,
四边形AEFB的周长=AE+EF+BF+AB,
四边形DEFC的周长=CF+EF+DE+CD,
∴四边形AEFB与四边形DEFC的周长相等.
(3)解:由(1)(2)可知△BOF≌△DOE,△COF≌△AOE.
又易证△AOB≌△COD,∴S四边形AEFB=S四边形DEFC.
即直线EF将?ABCD的面积二等分.
应用:连接AC,BD交于点O,作直线OP,则直线OP两旁的四边形面积相等(图略).
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
