2018年高考数学(文)二轮复习+专题突破训练:(高考22题)标准练4
文档属性
| 名称 | 2018年高考数学(文)二轮复习+专题突破训练:(高考22题)标准练4 |  | |
| 格式 | zip | ||
| 文件大小 | 211.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-12-13 19:55:28 | ||
图片预览



文档简介
12+4“80分”标准练4
1.(2017届山东师大附中模拟)已知集合A={x|y=lg(x+1)},B={x||x|<2},则A∩B等于( )
A.(-2,0) B.(0,2)
C.(-1,2) D.(-2,-1)
答案 C
解析 由x+1>0,得x>-1,
∴A=(-1,+∞),B={x||x|<2}=(-2,2),
∴A∩B=(-1,2).故选C.
2.(2017·山东)已知i是虚数单位,若复数z满足zi=1+i,则z2等于( )
A.-2i B.2i C.-2 D.2
答案 A
解析 方法一 z===1-i,
z2=(1-i)2=-2i.
方法二 (zi)2=(1+i)2,-z2=2i,z2=-2i.故选A.
3.(2017届山东省青岛市二模)已知命题p,q,“綈p为假”是“p∨q为真”的( )
A.充分不必要条件
B.必要不充分条件
C.充要条件
D.既不充分也不必要条件
答案 A
解析 若綈p为假,则p为真,则p∨q为真,即充分性成立,当p假q真时,满足p∨q为真,但綈p为真,则必要性不成立,21教育网
所以“綈p为假”是“p∨q为真”的充分不必要条件,
故选A.
4.已知x=ln π,,,则( )
A.x<y<z B.z<x<y
C.z<y<x D.y<z<x
答案 D
解析 x=ln π>1,
∴x>z>y.故选D.
5.(2017届山东省济宁市二模)过圆锥顶点的平面截去圆锥一部分,所得几何体的三视图如图所示,则原圆锥的体积为( )www.21-cn-jy.com
A.1 B.
C. D.
答案 D
解析 由三视图可得底面圆的半径为=2,圆锥的高为=2,
∴原圆锥的体积为π·22·2=,故选D.
6.(2017届广东省深圳市二模)一个三位数,个位、十位、百位上的数字依次为x,y,z,当且仅当y>x,y>z时,称这样的数为“凸数”(如243),现从集合{1,2,3,4}中取出三个不相同的数组成一个三位数,则这个三位数是“凸数”的概率为( )21·世纪*教育网
A. B.
C. D.
答案 B
解析 在{1,2,3,4}的4个整数中任取3个不同的数组成三位数,有24种情况,
在{1,2,3,4}的4个整数中任取3个不同的数,将最大的放在十位上,剩余的2个数字分别放在百、个位上,有8种情况,则这个三位数是“凸数”的概率是=.www-2-1-cnjy-com
故选B.
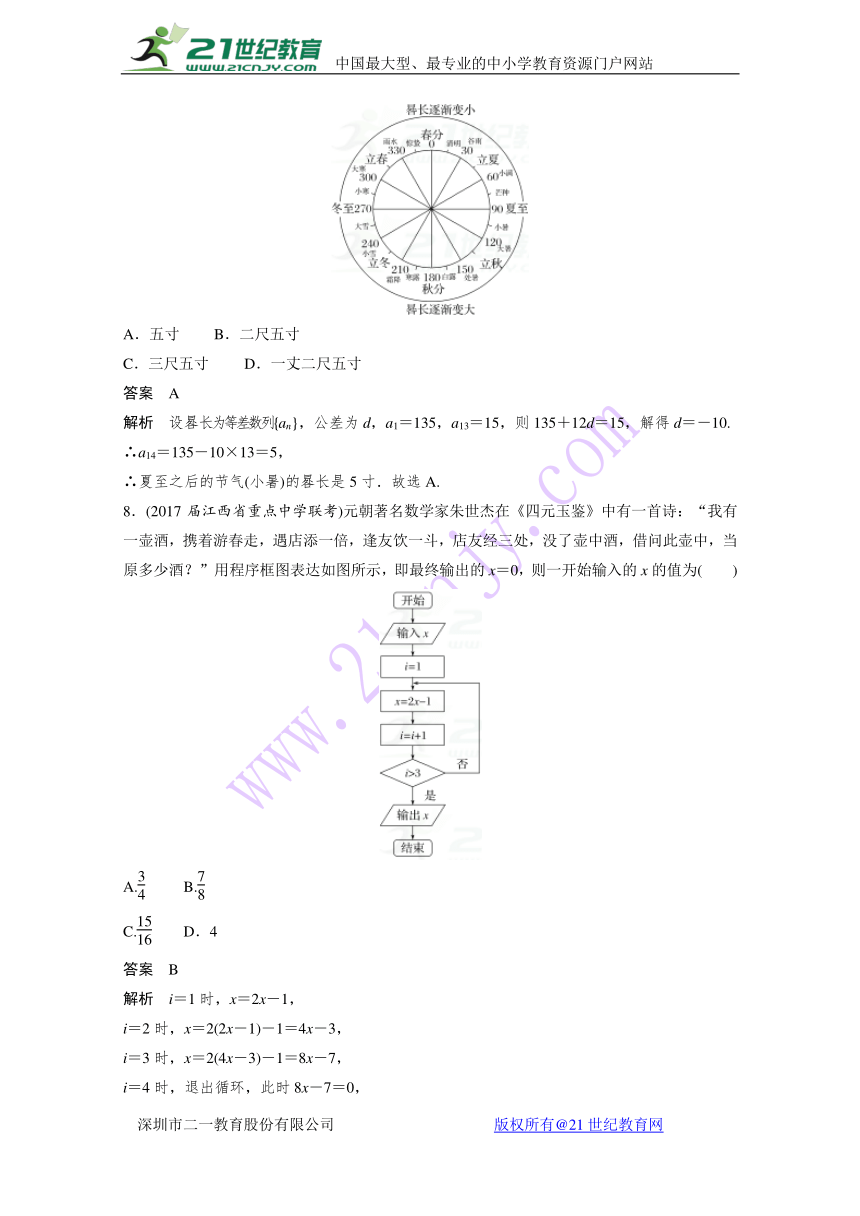
7.(2017届安徽省合肥市三模)《周髀算经》是中国古代的天文学和数学著作.其中一个问题大意为:一年有二十四个节气,每个节气晷长损益相同(即太阳照射物体影子的长度增加和减少大小相同).若冬至晷长一丈三尺五寸,夏至晷长一尺五寸(注:一丈等于十尺,一尺等于十寸),则夏至之后的节气(小暑)晷长为( )2-1-c-n-j-y
A.五寸 B.二尺五寸
C.三尺五寸 D.一丈二尺五寸
答案 A
解析 设晷长为等差数列{an},公差为d,a1=135,a13=15,则135+12d=15,解得d=-10.
∴a14=135-10×13=5,
∴夏至之后的节气(小暑)的晷长是5寸.故选A.
8.(2017届江西省重点中学联考)元朝著名数学家朱世杰在《四元玉鉴》中有一首诗:“我有一壶酒,携着游春走,遇店添一倍,逢友饮一斗,店友经三处,没了壶中酒,借问此壶中,当原多少酒?”用程序框图表达如图所示,即最终输出的x=0,则一开始输入的x的值为( )
A. B.
C. D.4
答案 B
解析 i=1时,x=2x-1,
i=2时,x=2(2x-1)-1=4x-3,
i=3时,x=2(4x-3)-1=8x-7,
i=4时,退出循环,此时8x-7=0,
解得x=,故选B.
9.(2017届山东省青岛市二模)已知函数f(x)=sin-cos2x+(x∈R),则下列说法正确的是( )2·1·c·n·j·y
A.函数f(x)的最小正周期为
B.函数f(x)的图象关于y轴对称
C.点为函数f(x)图象的一个对称中心
D.函数f(x)的最大值为
答案 D
解析 函数f(x)=sin-cos2x+
=-+
=sin 2x+cos 2x
=sin(x∈R),
由ω=2知,f(x)的最小正周期为π,A错误;
∵f(0)=sin =不是最值,
∴f(x)的图象不关于y轴对称,B错误;
∵f?=sin =≠0,
∴点不是函数f(x)图象的一个对称中心,C错误;
∵sin∈[-1,1],
∴f(x)的最大值是,D正确.
故选D.
10.(2017届山东省、湖北省部分重点中学模拟)已知实数x,y满足不等式组若目标函数z=y-mx取得最大值时有唯一的最优解(1,3),则实数m的取值范围是( )
A.m<-1 B.0<m<1
C.m>1 D.m≥1
答案 C
解析 作出不等式组对应的平面区域如图,
由z=y-mx,得y=mx+z,即直线的截距最大,z也最大,
若m=0,此时y=z,不满足条件;
若m>0,目标函数y=mx+z的斜率k=m>0,要使目标函数z=y-mx取得最大值时有唯一的最优解(1,3),21*cnjy*com
则直线y=mx+z的斜率m>1,
若m<0,目标函数y=mx+z的斜率k=m<0,不满足题意.
综上,m>1.
故选C.
11.已知双曲线C:-=1(a>0,b>0),过点P(3,6)的直线l与C相交于A,B两点,且AB的中点为N(12,15),则双曲线C的离心率为( )21cnjy.com
A.2 B.
C. D.
答案 B
解析 方法一 设A(x1,y1),B(x2,y2),
由AB的中点为N(12,15),得x1+x2=24,y1+y2=30,
由
两式相减得
=,
则==,
由直线AB的斜率k==1,
∴=1,则=,
双曲线的离心率e== =,
∴双曲线C的离心率为,故选B.
方法二 设A(12+m,15+n),B(12-m,15-n),
则
两式相减得=,
由直线l的斜率k==,
直线AB的斜率k==1,
∴=1,则=,
双曲线的离心率e== =,
∴双曲线C的离心率为,故选B.
12.(2017届安徽省合肥市三模)已知实数a,b满足2<a<b<3,下列不等关系中一定成立的是( )21世纪教育网版权所有
A.a3+15b>b3+15a
B.a3+15b<b3+15a
C.b·2a>a·2b
D.b·2a<a·2b
答案 D
解析 设f(x)=x3-15x,
则f′(x)=3x2-15=3(x+)(x-).
当x∈(2,)时,f′(x)<0,f(x)单调递减,
当x∈(,3)时,f′(x)>0,f(x)单调递增.
若2<a<b<,则f(a)>f(b),
即a3+15b>b3+15a;
若<a<b<3,则f(a)<f(b),
即a3+15b<b3+15a.
∴A,B均不一定成立.
设g(x)=,
则g′(x)==.
令g′(x)=0,得x=log2e∈(1,2).
∴当x∈(2,3)时,g′(x)>0,g(x)为增函数,
∵2<a<b<3,>,即b·2a<a·2b.
故选D.
13.(2017·全国Ⅲ)已知向量a=(-2,3),b=(3,m),且a⊥b,则m=________.
答案 2
解析 ∵a=(-2,3),b=(3,m),且a⊥b,
∴a·b=0,即-2×3+3m=0,解得m=2.
14.(2017届江苏省苏、锡、常、镇四市二模)已知直线l:mx+y-2m-1=0,圆C:x2+y2-2x-4y=0,当直线l被圆C所截得的弦长最短时,实数m=________.
答案 -1
解析 由圆C:x2+y2-2x-4y=0,
得(x-1)2+(y-2)2=5,
∴圆心坐标是C(1,2),半径是,
∵直线l:mx+y-2m-1=0过定点P(2,1),且在圆内,
∴当l⊥PC时,直线l被圆x2+y2-2x-4y=0截得的弦长最短,
∴-m·=-1,∴m=-1.
15.(2017届山东省聊城市三模)若函数f(x)=(x2-ax+a+1)ex(a∈N)在区间(1,3)上只有1个极值点,则曲线f(x)在点(0,f(0))处切线的方程为____________.21·cn·jy·com
答案 x-y+6=0
解析 f′(x)=ex[x2+(2-a)x+1],
若f(x)在(1,3)上只有1个极值点,
则f′(1)·f′(3)<0,
即(a-4)(3a-16)<0,
解得4<a<,a∈N,
故a=5,
故f(x)=ex(x2-5x+6),f′(x)=ex(x2-3x+1),
故f(0)=6,f′(0)=1,
故切线方程是y-6=x,即x-y+6=0.
16.(2017届上海市松江区二模)已知递增数列{an}共有2 017项,且各项均不为零,a2 017=1,如果从{an}中任取两项ai,aj,当i答案 1 009
解析 ∵当i∴an-an-1∴必有an-an-1=a1,an-an-2=a2,…,an-a1=an-1,
利用累加法可得(n-1)an=2(a1+a2+…+an-1),
故Sn-1=,S2 016=×1=1 008,
∴S2 017=S2 016+a2 017=1 008+1=1 009.
1.(2017届山东师大附中模拟)已知集合A={x|y=lg(x+1)},B={x||x|<2},则A∩B等于( )
A.(-2,0) B.(0,2)
C.(-1,2) D.(-2,-1)
答案 C
解析 由x+1>0,得x>-1,
∴A=(-1,+∞),B={x||x|<2}=(-2,2),
∴A∩B=(-1,2).故选C.
2.(2017·山东)已知i是虚数单位,若复数z满足zi=1+i,则z2等于( )
A.-2i B.2i C.-2 D.2
答案 A
解析 方法一 z===1-i,
z2=(1-i)2=-2i.
方法二 (zi)2=(1+i)2,-z2=2i,z2=-2i.故选A.
3.(2017届山东省青岛市二模)已知命题p,q,“綈p为假”是“p∨q为真”的( )
A.充分不必要条件
B.必要不充分条件
C.充要条件
D.既不充分也不必要条件
答案 A
解析 若綈p为假,则p为真,则p∨q为真,即充分性成立,当p假q真时,满足p∨q为真,但綈p为真,则必要性不成立,21教育网
所以“綈p为假”是“p∨q为真”的充分不必要条件,
故选A.
4.已知x=ln π,,,则( )
A.x<y<z B.z<x<y
C.z<y<x D.y<z<x
答案 D
解析 x=ln π>1,
∴x>z>y.故选D.
5.(2017届山东省济宁市二模)过圆锥顶点的平面截去圆锥一部分,所得几何体的三视图如图所示,则原圆锥的体积为( )www.21-cn-jy.com
A.1 B.
C. D.
答案 D
解析 由三视图可得底面圆的半径为=2,圆锥的高为=2,
∴原圆锥的体积为π·22·2=,故选D.
6.(2017届广东省深圳市二模)一个三位数,个位、十位、百位上的数字依次为x,y,z,当且仅当y>x,y>z时,称这样的数为“凸数”(如243),现从集合{1,2,3,4}中取出三个不相同的数组成一个三位数,则这个三位数是“凸数”的概率为( )21·世纪*教育网
A. B.
C. D.
答案 B
解析 在{1,2,3,4}的4个整数中任取3个不同的数组成三位数,有24种情况,
在{1,2,3,4}的4个整数中任取3个不同的数,将最大的放在十位上,剩余的2个数字分别放在百、个位上,有8种情况,则这个三位数是“凸数”的概率是=.www-2-1-cnjy-com
故选B.
7.(2017届安徽省合肥市三模)《周髀算经》是中国古代的天文学和数学著作.其中一个问题大意为:一年有二十四个节气,每个节气晷长损益相同(即太阳照射物体影子的长度增加和减少大小相同).若冬至晷长一丈三尺五寸,夏至晷长一尺五寸(注:一丈等于十尺,一尺等于十寸),则夏至之后的节气(小暑)晷长为( )2-1-c-n-j-y
A.五寸 B.二尺五寸
C.三尺五寸 D.一丈二尺五寸
答案 A
解析 设晷长为等差数列{an},公差为d,a1=135,a13=15,则135+12d=15,解得d=-10.
∴a14=135-10×13=5,
∴夏至之后的节气(小暑)的晷长是5寸.故选A.
8.(2017届江西省重点中学联考)元朝著名数学家朱世杰在《四元玉鉴》中有一首诗:“我有一壶酒,携着游春走,遇店添一倍,逢友饮一斗,店友经三处,没了壶中酒,借问此壶中,当原多少酒?”用程序框图表达如图所示,即最终输出的x=0,则一开始输入的x的值为( )
A. B.
C. D.4
答案 B
解析 i=1时,x=2x-1,
i=2时,x=2(2x-1)-1=4x-3,
i=3时,x=2(4x-3)-1=8x-7,
i=4时,退出循环,此时8x-7=0,
解得x=,故选B.
9.(2017届山东省青岛市二模)已知函数f(x)=sin-cos2x+(x∈R),则下列说法正确的是( )2·1·c·n·j·y
A.函数f(x)的最小正周期为
B.函数f(x)的图象关于y轴对称
C.点为函数f(x)图象的一个对称中心
D.函数f(x)的最大值为
答案 D
解析 函数f(x)=sin-cos2x+
=-+
=sin 2x+cos 2x
=sin(x∈R),
由ω=2知,f(x)的最小正周期为π,A错误;
∵f(0)=sin =不是最值,
∴f(x)的图象不关于y轴对称,B错误;
∵f?=sin =≠0,
∴点不是函数f(x)图象的一个对称中心,C错误;
∵sin∈[-1,1],
∴f(x)的最大值是,D正确.
故选D.
10.(2017届山东省、湖北省部分重点中学模拟)已知实数x,y满足不等式组若目标函数z=y-mx取得最大值时有唯一的最优解(1,3),则实数m的取值范围是( )
A.m<-1 B.0<m<1
C.m>1 D.m≥1
答案 C
解析 作出不等式组对应的平面区域如图,
由z=y-mx,得y=mx+z,即直线的截距最大,z也最大,
若m=0,此时y=z,不满足条件;
若m>0,目标函数y=mx+z的斜率k=m>0,要使目标函数z=y-mx取得最大值时有唯一的最优解(1,3),21*cnjy*com
则直线y=mx+z的斜率m>1,
若m<0,目标函数y=mx+z的斜率k=m<0,不满足题意.
综上,m>1.
故选C.
11.已知双曲线C:-=1(a>0,b>0),过点P(3,6)的直线l与C相交于A,B两点,且AB的中点为N(12,15),则双曲线C的离心率为( )21cnjy.com
A.2 B.
C. D.
答案 B
解析 方法一 设A(x1,y1),B(x2,y2),
由AB的中点为N(12,15),得x1+x2=24,y1+y2=30,
由
两式相减得
=,
则==,
由直线AB的斜率k==1,
∴=1,则=,
双曲线的离心率e== =,
∴双曲线C的离心率为,故选B.
方法二 设A(12+m,15+n),B(12-m,15-n),
则
两式相减得=,
由直线l的斜率k==,
直线AB的斜率k==1,
∴=1,则=,
双曲线的离心率e== =,
∴双曲线C的离心率为,故选B.
12.(2017届安徽省合肥市三模)已知实数a,b满足2<a<b<3,下列不等关系中一定成立的是( )21世纪教育网版权所有
A.a3+15b>b3+15a
B.a3+15b<b3+15a
C.b·2a>a·2b
D.b·2a<a·2b
答案 D
解析 设f(x)=x3-15x,
则f′(x)=3x2-15=3(x+)(x-).
当x∈(2,)时,f′(x)<0,f(x)单调递减,
当x∈(,3)时,f′(x)>0,f(x)单调递增.
若2<a<b<,则f(a)>f(b),
即a3+15b>b3+15a;
若<a<b<3,则f(a)<f(b),
即a3+15b<b3+15a.
∴A,B均不一定成立.
设g(x)=,
则g′(x)==.
令g′(x)=0,得x=log2e∈(1,2).
∴当x∈(2,3)时,g′(x)>0,g(x)为增函数,
∵2<a<b<3,>,即b·2a<a·2b.
故选D.
13.(2017·全国Ⅲ)已知向量a=(-2,3),b=(3,m),且a⊥b,则m=________.
答案 2
解析 ∵a=(-2,3),b=(3,m),且a⊥b,
∴a·b=0,即-2×3+3m=0,解得m=2.
14.(2017届江苏省苏、锡、常、镇四市二模)已知直线l:mx+y-2m-1=0,圆C:x2+y2-2x-4y=0,当直线l被圆C所截得的弦长最短时,实数m=________.
答案 -1
解析 由圆C:x2+y2-2x-4y=0,
得(x-1)2+(y-2)2=5,
∴圆心坐标是C(1,2),半径是,
∵直线l:mx+y-2m-1=0过定点P(2,1),且在圆内,
∴当l⊥PC时,直线l被圆x2+y2-2x-4y=0截得的弦长最短,
∴-m·=-1,∴m=-1.
15.(2017届山东省聊城市三模)若函数f(x)=(x2-ax+a+1)ex(a∈N)在区间(1,3)上只有1个极值点,则曲线f(x)在点(0,f(0))处切线的方程为____________.21·cn·jy·com
答案 x-y+6=0
解析 f′(x)=ex[x2+(2-a)x+1],
若f(x)在(1,3)上只有1个极值点,
则f′(1)·f′(3)<0,
即(a-4)(3a-16)<0,
解得4<a<,a∈N,
故a=5,
故f(x)=ex(x2-5x+6),f′(x)=ex(x2-3x+1),
故f(0)=6,f′(0)=1,
故切线方程是y-6=x,即x-y+6=0.
16.(2017届上海市松江区二模)已知递增数列{an}共有2 017项,且各项均不为零,a2 017=1,如果从{an}中任取两项ai,aj,当i
解析 ∵当i
利用累加法可得(n-1)an=2(a1+a2+…+an-1),
故Sn-1=,S2 016=×1=1 008,
∴S2 017=S2 016+a2 017=1 008+1=1 009.
同课章节目录
