2.2 二次函数的图象与性质(1)一课一测
文档属性
| 名称 | 2.2 二次函数的图象与性质(1)一课一测 |  | |
| 格式 | doc | ||
| 文件大小 | 512.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-12-22 10:32:11 | ||
图片预览


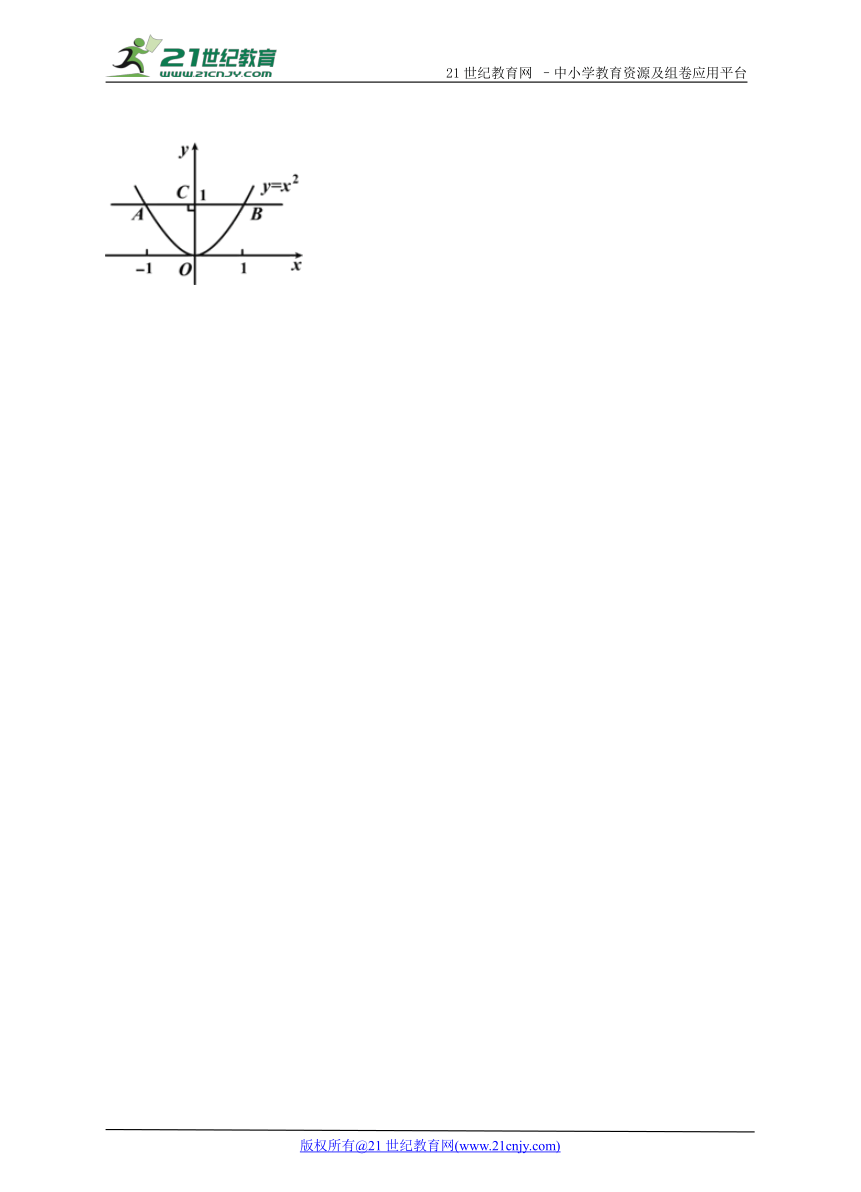

文档简介
21世纪教育网 –中小学教育资源及组卷应用平台
2.2 二次函数的图象与性质
第一课时检测
(时间45分钟 满分100分)
一.选择题(每小题6分,共48分)
1.(2017秋 瑶海区期中)抛物线y=x2,当﹣1≤x≤3时,y的取值范围是( )
A.﹣1≤y≤9 B.0≤y≤9 C.1≤y≤9 D.﹣1≤y≤3
2.(2017秋 和政县校级月考)关于函数y=x2的性质表达正确的一项是( )
A.无论x为任何实数,y值总为正
B.当x值增大时,y的值也增大
C.它的图象关于y轴对称
D.它的图象在第一、三象限内
3.(2016秋 宁河县月考)抛物线y=﹣x2不具有的性质是( )
A.开口向上
B.对称轴是y轴
C.在对称轴的左侧,y随x的增大而增大
D.最高点是原点
4.(2016秋 德城区校级月考)已知a<﹣1,点(a﹣1,y1),(a,y2),(a+1,y3)都在函数y=﹣x2的图象上,则( )21世纪教育网版权所有
A.y1<y2<y3 B.y1<y3<y2 C.y3<y2<y1 D.y2<y1<y3
5.(2015秋 长汀县期中)已知a<﹣2,点(a﹣1,y1),(a,y2),(a+1,y3)都在函数y=x2的图象上,则( )2·1·c·n·j·y
A.y1<y2<y3 B.y1<y3<y2 C.y3<y2<y1 D.y2<y1<y3
6.(2015秋 黄陂区校级月考)如图, ( http: / / www.21cnjy.com )点A1、A2、A3、…、An在抛物线y=x2图象上,点B1、B2、B3、…、Bn在y轴上,若△A1B0B1、△A2B1B2、…、△AnBn﹣1Bn都为等腰直角三角形(点B0是坐标原点),则△A2014B2013B2014的腰长等于( )
( http: / / www.21cnjy.com )
A.2013 B.2014 C.2013 ( http: / / www.21cnjy.com ) D.2014 ( http: / / www.21cnjy.com )
7.(2014 道外区二模)如图,点A在x轴正半轴上,抛物线y=x2与直线y=4在第一象限内的交点为B,则tan∠AOB的值为( )www-2-1-cnjy-com
( http: / / www.21cnjy.com )
A.1 B.2 C.3 D.4
8.(2015 蓬安县校级自主招生)给出下列命题及函数y=x与y=x2和 ( http: / / www.21cnjy.com )的图象:
①如果 ( http: / / www.21cnjy.com )>a>a2,那么0<a<1;
②如果a2>a ( http: / / www.21cnjy.com ),那么a>1或﹣1<a<0;
③如果 ( http: / / www.21cnjy.com )>a2>a,那么﹣1<a<0;
④如果a2> ( http: / / www.21cnjy.com )>a,那么a<﹣1.则( )
( http: / / www.21cnjy.com )
A.正确的命题只有① B.正确的命题有①②④
C.错误的命题有②③ D.错误的命题是③④
二.填空题(每小题6分,共30分)
9.(2016秋 三亚期中)二次函数y=x ( http: / / www.21cnjy.com )2的图象开口方向 .当x= 时,y有最 值,是 ,当x<0时,y随x的增大而 .
10.(2016秋 孝南区校级月考)二次函数y=﹣x2的图象,在y轴的右边,y随x的增大而 .【来源:21·世纪·教育·网】
11.观察二次函数y=x2的图象,并填空.当x<0时,随着x值的增大,y的值 ;当x>0时,随着x值的增大,y的值 .【来源:21cnj*y.co*m】
( http: / / www.21cnjy.com )
12.二次函数y=x2的图象是一条 ,它的开口向 ,它的对称轴为 ,它的顶点坐标为 .【出处:21教育名师】
( http: / / www.21cnjy.com )
13.点A(5,y1)和B(2,y2)都在抛物线y=﹣x2上,则y1与y2的关系是 .
三.解答题(共22分)
14.(10分)画出二次函数y=x2的图象.
15. (12分) 如图,已知抛物线y=x2上有一点A,A点的横坐标是-1,过点A作AB∥x轴,交抛物线于另一点B,求△AOB的面积.21教育名师原创作品
2.2 二次函数的图象与性质
第一课时检测
(时间45分钟 满分100分)
参考答案与试题解析
一.选择题(每小题6分,共48分)
1.(2017秋 瑶海区期中)抛物线y=x2,当﹣1≤x≤3时,y的取值范围是( )
A.﹣1≤y≤9 B.0≤y≤9 C.1≤y≤9 D.﹣1≤y≤3
【分析】由抛物线开口方向、对称轴及增减性求得其最大和最小值即可求得答案.
【解答】解:
∵y=x2,
∴抛物线开口向上,对称轴为y轴,
∴当﹣1≤x≤0时,y随x的增大而减小,故当x=﹣1时,y有最大值1,当x=0时,y有最小值0;
当0≤x≤3时,y随x的增大而增大,故当x=3时,y有阳大值9,当x=0时,y有最小值0;
∴当﹣1≤x≤3时,y的取值范围是0≤y≤9,
故选B.
2.(2017秋 和政县校级月考)关于函数y=x2的性质表达正确的一项是( )
A.无论x为任何实数,y值总为正
B.当x值增大时,y的值也增大
C.它的图象关于y轴对称
D.它的图象在第一、三象限内
【分析】根据形如y=ax2(a≠0)的二次函数的性质直接判断即可.
【解答】解:二次函数y=x2的图象开口向上,对称轴为y轴.
故选C.
3.(2016秋 宁河县月考)抛物线y=﹣x2不具有的性质是( )
A.开口向上
B.对称轴是y轴
C.在对称轴的左侧,y随x的增大而增大
D.最高点是原点
【分析】此题应从二次函数的基本形式入手,它符合y=ax2的基本形式,根据它的性质,进行解答.
【解答】解:因为a<0,所以开口向下,顶点坐标(0,0),对称轴是y轴,有最高点是原点.
故选:A
4.(2016秋 德城区校级月考)已知a<﹣1,点(a﹣1,y1),(a,y2),(a+1,y3)都在函数y=﹣x2的图象上,则( )21教育网
A.y1<y2<y3 B.y1<y3<y2 C.y3<y2<y1 D.y2<y1<y3
【分析】二次函数抛物线向下,且对称轴为y轴,根据在对称轴的左侧,y随x的增大而增大即可判断纵坐标的大小.21·cn·jy·com
【解答】解:∵二次函数y=﹣x2,
∴该二次函数的抛物线开口向下,且对称轴为:x=0,即y轴.
∵a<﹣1,
∴a﹣1<a<a+1<0,
∵在对称轴的左侧,y随x的增大而增大,
∴y1<y2<y3.
故选A.
5.(2015秋 长汀县期中)已知a<﹣2,点(a﹣1,y1),(a,y2),(a+1,y3)都在函数y=x2的图象上,则( )21cnjy.com
A.y1<y2<y3 B.y1<y3<y2 C.y3<y2<y1 D.y2<y1<y3
【分析】由a<﹣2即可得出a﹣1<a<a+ ( http: / / www.21cnjy.com )1<﹣1,再根据在函数y=x2的图象上,当x<0时,y随着x的增大而减小,由此即可得出y1<y2<y3.
【解答】解:∵a<﹣2,
∴a﹣1<a<a+1<﹣1.
∵在函数y=x2的图象上,当x<0时,y随着x的增大而减小,
∴y1<y2<y3.
故选C.
6.(2015秋 黄陂区校 ( http: / / www.21cnjy.com )级月考)如图,点A1、A2、A3、…、An在抛物线y=x2图象上,点B1、B2、B3、…、Bn在y轴上,若△A1B0B1、△A2B1B2、…、△AnBn﹣1Bn都为等腰直角三角形(点B0是坐标原点),则△A2014B2013B2014的腰长等于( )
( http: / / www.21cnjy.com )
A.2013 B.2014 C.2013 ( http: / / www.21cnjy.com ) D.2014 ( http: / / www.21cnjy.com )
【分析】利用等腰直角三角形的性质及点的 ( http: / / www.21cnjy.com )坐标的关系求出第一个等腰直角三角形的腰长,用类似的方法求出第二个,第三个…的腰长,观察其规律,最后得出结果.21·世纪*教育网
【解答】解:作A1C⊥y轴,A2E⊥y轴,垂足分别为C、E,
∵△A1B0B1、△A2B1B2都是等腰直角三角形,
∴B1C=B0C=DB0=A1D,B2E=B1E,
设A1(a,a),
将点A1的坐标代入解析式y=x2得:a=a2,
解得:a=0(不符合题意)或a=1,由勾股定理得:A1B0= ( http: / / www.21cnjy.com ),
则B1B0=2,
过B1作B1N⊥A2F,设点A2(x2,y2),
可得A2N=y2﹣2,B1N=x2=y2﹣2,
又点A2在抛物线上,所以y2=x22,即(x2+2)=x22,
解得x2=2,x2=﹣1(不合题意舍去),
则A2B1=2 ( http: / / www.21cnjy.com ),同理可得:A3B2=3 ( http: / / www.21cnjy.com ),A4B3=4 ( http: / / www.21cnjy.com )…
∴A2014B2013=2014 ( http: / / www.21cnjy.com ),
∴△A2014B2013B2014的腰长为:2014 ( http: / / www.21cnjy.com ).
故选D.
( http: / / www.21cnjy.com )
7.(2014 道外区二模)如图,点A在x轴正半轴上,抛物线y=x2与直线y=4在第一象限内的交点为B,则tan∠AOB的值为( )2-1-c-n-j-y
( http: / / www.21cnjy.com )
A.1 B.2 C.3 D.4
【分析】把y=4代入二次函数解析式求出x的值,得到点B的坐标,然后根据正切值的定义列式计算即可得解.21*cnjy*com
【解答】解:y=4时,x2=4,
解得x1=2,x2=﹣2(舍去),
∴点B的坐标为(2,4),
∴tan∠AOB= ( http: / / www.21cnjy.com )=2.
故选B.
8.(2015 蓬安县校级自主招生)给出下列命题及函数y=x与y=x2和 ( http: / / www.21cnjy.com )的图象:
①如果 ( http: / / www.21cnjy.com )>a>a2,那么0<a<1;
②如果a2>a ( http: / / www.21cnjy.com ),那么a>1或﹣1<a<0;
③如果 ( http: / / www.21cnjy.com )>a2>a,那么﹣1<a<0;
④如果a2> ( http: / / www.21cnjy.com )>a,那么a<﹣1.则( )
( http: / / www.21cnjy.com )
A.正确的命题只有① B.正确的命题有①②④
C.错误的命题有②③ D.错误的命题是③④
【分析】利用函数结合解析式可得出其交点坐标为(1,1),进而结合图象分析得出即可.
【解答】解:①如果 ( http: / / www.21cnjy.com )>a>a2,那么0<a<1,正确;
②如果a2>a ( http: / / www.21cnjy.com ),那么a>1或﹣1<a<0,正确;
③如果 ( http: / / www.21cnjy.com )>a2>a,那么﹣1<a<0,错误;
④如果a2> ( http: / / www.21cnjy.com )>a,那么a<﹣1,正确,
故选:B.
二.填空题(每小题6分,共30分)
9.(2016秋 三亚期中)二次函 ( http: / / www.21cnjy.com )数y=x2的图象开口方向 向上 .当x= 0 时,y有最 小 值,是 0 ,当x<0时,y随x的增大而 减小 .
【分析】二次函数y=ax2+bx+ ( http: / / www.21cnjy.com )c (a,b,c为常数,a≠0)且a决定函数的开口方向,a>0时,开口方向向上,a<0时,开口方向向下.在顶点处,y具有最大或最小值,在对称轴的两侧,y随x的变化相反.【版权所有:21教育】
【解答】解:二次函数y=x2的图象开口方向向上,当x=0时,y有最小值,是0,当x<0时,y随x的增大而减小.
10.(2016秋 孝南区校级月考)二次函数y=﹣x2的图象,在y轴的右边,y随x的增大而 减小 .
【分析】二次函数y=﹣x2的对称轴是y轴,所以在y轴的右边,y随x的增大而减小.
【解答】解:∵a=﹣1,
∴函数图象开口向下,且对称轴是y轴.
∴在y轴的右边y随x的增大而减小.
故答案为:减小.
11.观察二次函数y=x2的图象,并填空.当x<0时,随着x值的增大,y的值 减小 ;当x>0时,随着x值的增大,y的值 增大 .
( http: / / www.21cnjy.com )
【分析】此题较简单,观察图象即可得出答案.
【解答】解:观察图象可知:当x<0时,随着x值的增大,y的值减小;
当x>0时,随着x值的增大,y的值增大.
12.二次函数y=x2的图象是一条 抛物线 ,它的开口向 上 ,它的对称轴为 y轴 ,它的顶点坐标为 (0,0) .21*cnjy*com
( http: / / www.21cnjy.com )
【分析】此题较简单,观察图象即可得出答案.
【解答】解:观察图象可知,
二次函数y=x2的图象是一条抛物线,
它的开口向上,它的对称轴为y轴,它的顶点坐标为(0,0).
13.(2014秋 鲅鱼圈区期末)点A(5, ( http: / / www.21cnjy.com )y1)和B(2,y2)都在抛物线y=﹣x2上,则y1与y2的关系是 y1<y2 .
A.y1≥y2 B.y1=y2 C.y1<y2 D.y1>y2
【分析】根据二次函数图象上点的坐标特征,分别计算出自变量为5和2所对应的函数值,然后比较函数值的大小即可.
【解答】解:∵点A(5,y1)和B(2,y2)都在抛物线y=﹣x2上,
∴y1=﹣25,y2=﹣4,
∴y1<y2.
三.解答题(共22分)
14.(10分)画出二次函数y=x2的图象.
【解答】解:函数y=x2的图象如图所示,
( http: / / www.21cnjy.com )
15. (12分) 如图,已知抛物线y=x2上有一点A,A点的横坐标是-1,过点A作AB∥x轴,交抛物线于另一点B,求△AOB的面积.www.21-cn-jy.com
【解答】解:如图,由y=(-1) 可得,y=1,则A(-1,1),所以B(1,1).故AB=2,OC=1,所以△AOB的面积=0.5×2×1=1
( http: / / www.21cnjy.com )
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://www.21cnjy.com/" 版权所有@21世纪教育网(www.21cnjy.com)
2.2 二次函数的图象与性质
第一课时检测
(时间45分钟 满分100分)
一.选择题(每小题6分,共48分)
1.(2017秋 瑶海区期中)抛物线y=x2,当﹣1≤x≤3时,y的取值范围是( )
A.﹣1≤y≤9 B.0≤y≤9 C.1≤y≤9 D.﹣1≤y≤3
2.(2017秋 和政县校级月考)关于函数y=x2的性质表达正确的一项是( )
A.无论x为任何实数,y值总为正
B.当x值增大时,y的值也增大
C.它的图象关于y轴对称
D.它的图象在第一、三象限内
3.(2016秋 宁河县月考)抛物线y=﹣x2不具有的性质是( )
A.开口向上
B.对称轴是y轴
C.在对称轴的左侧,y随x的增大而增大
D.最高点是原点
4.(2016秋 德城区校级月考)已知a<﹣1,点(a﹣1,y1),(a,y2),(a+1,y3)都在函数y=﹣x2的图象上,则( )21世纪教育网版权所有
A.y1<y2<y3 B.y1<y3<y2 C.y3<y2<y1 D.y2<y1<y3
5.(2015秋 长汀县期中)已知a<﹣2,点(a﹣1,y1),(a,y2),(a+1,y3)都在函数y=x2的图象上,则( )2·1·c·n·j·y
A.y1<y2<y3 B.y1<y3<y2 C.y3<y2<y1 D.y2<y1<y3
6.(2015秋 黄陂区校级月考)如图, ( http: / / www.21cnjy.com )点A1、A2、A3、…、An在抛物线y=x2图象上,点B1、B2、B3、…、Bn在y轴上,若△A1B0B1、△A2B1B2、…、△AnBn﹣1Bn都为等腰直角三角形(点B0是坐标原点),则△A2014B2013B2014的腰长等于( )
( http: / / www.21cnjy.com )
A.2013 B.2014 C.2013 ( http: / / www.21cnjy.com ) D.2014 ( http: / / www.21cnjy.com )
7.(2014 道外区二模)如图,点A在x轴正半轴上,抛物线y=x2与直线y=4在第一象限内的交点为B,则tan∠AOB的值为( )www-2-1-cnjy-com
( http: / / www.21cnjy.com )
A.1 B.2 C.3 D.4
8.(2015 蓬安县校级自主招生)给出下列命题及函数y=x与y=x2和 ( http: / / www.21cnjy.com )的图象:
①如果 ( http: / / www.21cnjy.com )>a>a2,那么0<a<1;
②如果a2>a ( http: / / www.21cnjy.com ),那么a>1或﹣1<a<0;
③如果 ( http: / / www.21cnjy.com )>a2>a,那么﹣1<a<0;
④如果a2> ( http: / / www.21cnjy.com )>a,那么a<﹣1.则( )
( http: / / www.21cnjy.com )
A.正确的命题只有① B.正确的命题有①②④
C.错误的命题有②③ D.错误的命题是③④
二.填空题(每小题6分,共30分)
9.(2016秋 三亚期中)二次函数y=x ( http: / / www.21cnjy.com )2的图象开口方向 .当x= 时,y有最 值,是 ,当x<0时,y随x的增大而 .
10.(2016秋 孝南区校级月考)二次函数y=﹣x2的图象,在y轴的右边,y随x的增大而 .【来源:21·世纪·教育·网】
11.观察二次函数y=x2的图象,并填空.当x<0时,随着x值的增大,y的值 ;当x>0时,随着x值的增大,y的值 .【来源:21cnj*y.co*m】
( http: / / www.21cnjy.com )
12.二次函数y=x2的图象是一条 ,它的开口向 ,它的对称轴为 ,它的顶点坐标为 .【出处:21教育名师】
( http: / / www.21cnjy.com )
13.点A(5,y1)和B(2,y2)都在抛物线y=﹣x2上,则y1与y2的关系是 .
三.解答题(共22分)
14.(10分)画出二次函数y=x2的图象.
15. (12分) 如图,已知抛物线y=x2上有一点A,A点的横坐标是-1,过点A作AB∥x轴,交抛物线于另一点B,求△AOB的面积.21教育名师原创作品
2.2 二次函数的图象与性质
第一课时检测
(时间45分钟 满分100分)
参考答案与试题解析
一.选择题(每小题6分,共48分)
1.(2017秋 瑶海区期中)抛物线y=x2,当﹣1≤x≤3时,y的取值范围是( )
A.﹣1≤y≤9 B.0≤y≤9 C.1≤y≤9 D.﹣1≤y≤3
【分析】由抛物线开口方向、对称轴及增减性求得其最大和最小值即可求得答案.
【解答】解:
∵y=x2,
∴抛物线开口向上,对称轴为y轴,
∴当﹣1≤x≤0时,y随x的增大而减小,故当x=﹣1时,y有最大值1,当x=0时,y有最小值0;
当0≤x≤3时,y随x的增大而增大,故当x=3时,y有阳大值9,当x=0时,y有最小值0;
∴当﹣1≤x≤3时,y的取值范围是0≤y≤9,
故选B.
2.(2017秋 和政县校级月考)关于函数y=x2的性质表达正确的一项是( )
A.无论x为任何实数,y值总为正
B.当x值增大时,y的值也增大
C.它的图象关于y轴对称
D.它的图象在第一、三象限内
【分析】根据形如y=ax2(a≠0)的二次函数的性质直接判断即可.
【解答】解:二次函数y=x2的图象开口向上,对称轴为y轴.
故选C.
3.(2016秋 宁河县月考)抛物线y=﹣x2不具有的性质是( )
A.开口向上
B.对称轴是y轴
C.在对称轴的左侧,y随x的增大而增大
D.最高点是原点
【分析】此题应从二次函数的基本形式入手,它符合y=ax2的基本形式,根据它的性质,进行解答.
【解答】解:因为a<0,所以开口向下,顶点坐标(0,0),对称轴是y轴,有最高点是原点.
故选:A
4.(2016秋 德城区校级月考)已知a<﹣1,点(a﹣1,y1),(a,y2),(a+1,y3)都在函数y=﹣x2的图象上,则( )21教育网
A.y1<y2<y3 B.y1<y3<y2 C.y3<y2<y1 D.y2<y1<y3
【分析】二次函数抛物线向下,且对称轴为y轴,根据在对称轴的左侧,y随x的增大而增大即可判断纵坐标的大小.21·cn·jy·com
【解答】解:∵二次函数y=﹣x2,
∴该二次函数的抛物线开口向下,且对称轴为:x=0,即y轴.
∵a<﹣1,
∴a﹣1<a<a+1<0,
∵在对称轴的左侧,y随x的增大而增大,
∴y1<y2<y3.
故选A.
5.(2015秋 长汀县期中)已知a<﹣2,点(a﹣1,y1),(a,y2),(a+1,y3)都在函数y=x2的图象上,则( )21cnjy.com
A.y1<y2<y3 B.y1<y3<y2 C.y3<y2<y1 D.y2<y1<y3
【分析】由a<﹣2即可得出a﹣1<a<a+ ( http: / / www.21cnjy.com )1<﹣1,再根据在函数y=x2的图象上,当x<0时,y随着x的增大而减小,由此即可得出y1<y2<y3.
【解答】解:∵a<﹣2,
∴a﹣1<a<a+1<﹣1.
∵在函数y=x2的图象上,当x<0时,y随着x的增大而减小,
∴y1<y2<y3.
故选C.
6.(2015秋 黄陂区校 ( http: / / www.21cnjy.com )级月考)如图,点A1、A2、A3、…、An在抛物线y=x2图象上,点B1、B2、B3、…、Bn在y轴上,若△A1B0B1、△A2B1B2、…、△AnBn﹣1Bn都为等腰直角三角形(点B0是坐标原点),则△A2014B2013B2014的腰长等于( )
( http: / / www.21cnjy.com )
A.2013 B.2014 C.2013 ( http: / / www.21cnjy.com ) D.2014 ( http: / / www.21cnjy.com )
【分析】利用等腰直角三角形的性质及点的 ( http: / / www.21cnjy.com )坐标的关系求出第一个等腰直角三角形的腰长,用类似的方法求出第二个,第三个…的腰长,观察其规律,最后得出结果.21·世纪*教育网
【解答】解:作A1C⊥y轴,A2E⊥y轴,垂足分别为C、E,
∵△A1B0B1、△A2B1B2都是等腰直角三角形,
∴B1C=B0C=DB0=A1D,B2E=B1E,
设A1(a,a),
将点A1的坐标代入解析式y=x2得:a=a2,
解得:a=0(不符合题意)或a=1,由勾股定理得:A1B0= ( http: / / www.21cnjy.com ),
则B1B0=2,
过B1作B1N⊥A2F,设点A2(x2,y2),
可得A2N=y2﹣2,B1N=x2=y2﹣2,
又点A2在抛物线上,所以y2=x22,即(x2+2)=x22,
解得x2=2,x2=﹣1(不合题意舍去),
则A2B1=2 ( http: / / www.21cnjy.com ),同理可得:A3B2=3 ( http: / / www.21cnjy.com ),A4B3=4 ( http: / / www.21cnjy.com )…
∴A2014B2013=2014 ( http: / / www.21cnjy.com ),
∴△A2014B2013B2014的腰长为:2014 ( http: / / www.21cnjy.com ).
故选D.
( http: / / www.21cnjy.com )
7.(2014 道外区二模)如图,点A在x轴正半轴上,抛物线y=x2与直线y=4在第一象限内的交点为B,则tan∠AOB的值为( )2-1-c-n-j-y
( http: / / www.21cnjy.com )
A.1 B.2 C.3 D.4
【分析】把y=4代入二次函数解析式求出x的值,得到点B的坐标,然后根据正切值的定义列式计算即可得解.21*cnjy*com
【解答】解:y=4时,x2=4,
解得x1=2,x2=﹣2(舍去),
∴点B的坐标为(2,4),
∴tan∠AOB= ( http: / / www.21cnjy.com )=2.
故选B.
8.(2015 蓬安县校级自主招生)给出下列命题及函数y=x与y=x2和 ( http: / / www.21cnjy.com )的图象:
①如果 ( http: / / www.21cnjy.com )>a>a2,那么0<a<1;
②如果a2>a ( http: / / www.21cnjy.com ),那么a>1或﹣1<a<0;
③如果 ( http: / / www.21cnjy.com )>a2>a,那么﹣1<a<0;
④如果a2> ( http: / / www.21cnjy.com )>a,那么a<﹣1.则( )
( http: / / www.21cnjy.com )
A.正确的命题只有① B.正确的命题有①②④
C.错误的命题有②③ D.错误的命题是③④
【分析】利用函数结合解析式可得出其交点坐标为(1,1),进而结合图象分析得出即可.
【解答】解:①如果 ( http: / / www.21cnjy.com )>a>a2,那么0<a<1,正确;
②如果a2>a ( http: / / www.21cnjy.com ),那么a>1或﹣1<a<0,正确;
③如果 ( http: / / www.21cnjy.com )>a2>a,那么﹣1<a<0,错误;
④如果a2> ( http: / / www.21cnjy.com )>a,那么a<﹣1,正确,
故选:B.
二.填空题(每小题6分,共30分)
9.(2016秋 三亚期中)二次函 ( http: / / www.21cnjy.com )数y=x2的图象开口方向 向上 .当x= 0 时,y有最 小 值,是 0 ,当x<0时,y随x的增大而 减小 .
【分析】二次函数y=ax2+bx+ ( http: / / www.21cnjy.com )c (a,b,c为常数,a≠0)且a决定函数的开口方向,a>0时,开口方向向上,a<0时,开口方向向下.在顶点处,y具有最大或最小值,在对称轴的两侧,y随x的变化相反.【版权所有:21教育】
【解答】解:二次函数y=x2的图象开口方向向上,当x=0时,y有最小值,是0,当x<0时,y随x的增大而减小.
10.(2016秋 孝南区校级月考)二次函数y=﹣x2的图象,在y轴的右边,y随x的增大而 减小 .
【分析】二次函数y=﹣x2的对称轴是y轴,所以在y轴的右边,y随x的增大而减小.
【解答】解:∵a=﹣1,
∴函数图象开口向下,且对称轴是y轴.
∴在y轴的右边y随x的增大而减小.
故答案为:减小.
11.观察二次函数y=x2的图象,并填空.当x<0时,随着x值的增大,y的值 减小 ;当x>0时,随着x值的增大,y的值 增大 .
( http: / / www.21cnjy.com )
【分析】此题较简单,观察图象即可得出答案.
【解答】解:观察图象可知:当x<0时,随着x值的增大,y的值减小;
当x>0时,随着x值的增大,y的值增大.
12.二次函数y=x2的图象是一条 抛物线 ,它的开口向 上 ,它的对称轴为 y轴 ,它的顶点坐标为 (0,0) .21*cnjy*com
( http: / / www.21cnjy.com )
【分析】此题较简单,观察图象即可得出答案.
【解答】解:观察图象可知,
二次函数y=x2的图象是一条抛物线,
它的开口向上,它的对称轴为y轴,它的顶点坐标为(0,0).
13.(2014秋 鲅鱼圈区期末)点A(5, ( http: / / www.21cnjy.com )y1)和B(2,y2)都在抛物线y=﹣x2上,则y1与y2的关系是 y1<y2 .
A.y1≥y2 B.y1=y2 C.y1<y2 D.y1>y2
【分析】根据二次函数图象上点的坐标特征,分别计算出自变量为5和2所对应的函数值,然后比较函数值的大小即可.
【解答】解:∵点A(5,y1)和B(2,y2)都在抛物线y=﹣x2上,
∴y1=﹣25,y2=﹣4,
∴y1<y2.
三.解答题(共22分)
14.(10分)画出二次函数y=x2的图象.
【解答】解:函数y=x2的图象如图所示,
( http: / / www.21cnjy.com )
15. (12分) 如图,已知抛物线y=x2上有一点A,A点的横坐标是-1,过点A作AB∥x轴,交抛物线于另一点B,求△AOB的面积.www.21-cn-jy.com
【解答】解:如图,由y=(-1) 可得,y=1,则A(-1,1),所以B(1,1).故AB=2,OC=1,所以△AOB的面积=0.5×2×1=1
( http: / / www.21cnjy.com )
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://www.21cnjy.com/" 版权所有@21世纪教育网(www.21cnjy.com)
