数学四年级下北师大版2运用三角形内角和解决问题 (共18张)
文档属性
| 名称 | 数学四年级下北师大版2运用三角形内角和解决问题 (共18张) |  | |
| 格式 | zip | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-06-13 08:34:44 | ||
图片预览






文档简介
课件18张PPT。第2单元 认识三角形和四边形四年级数学·下 新课标[北师]3 探索与发现:三角形内角和第2课时 运用三角形内角和解决问题 填一填。
(1)三角形的内角和是( )。
(2)三角形按边分可分为( )、
( )。三角形按角分可分为
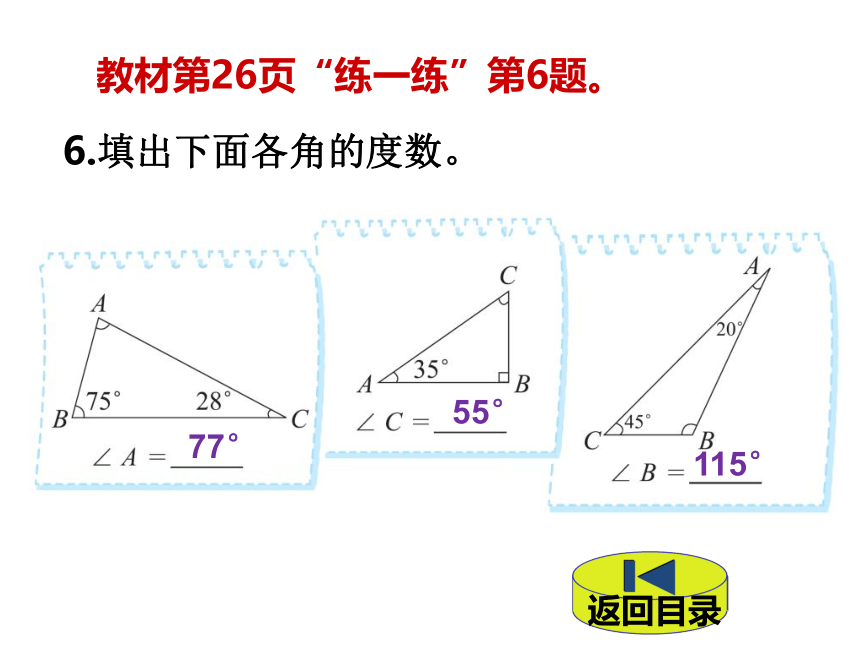
( )、( )和( )。180°等边三角形不等边三角形锐角三角形直角三角形钝角三角形学 习 新 知 早在300多年前就有一位伟大的数学家用科学的数学方法见证了任意三角形的内角和都是180度。这位伟大的数学家就是帕斯卡,他是法国著名的数学家、物理学家。他在12岁时发现了三角形内角和定律。猜一猜,可能是什么三角形?180°-60°-40°=80°锐角三角形你还能猜出是什么三角形?5.它们说的对吗?教材第26页“练一练”第5题。钝角三角形说得不对,钝角三角形两个锐角之和小于90°。直角三角形说得对。6.填出下面各角的度数。教材第26页“练一练”第6题。77°55°115°1.我们可以根据三角形内角和的性质,求出三角形中的未知角的度数。2.我们知道等腰三角形的一个顶角度数,就可以求出一个底角的度数。3.我们可以根据一个或者两个角的度数,推测出三角形的类型。让我仔细想一想!教材第26页“练一练”第7题。 7.挑战自我:探索四边形内角和。1.(基础题)填一填。(1)在一个直角三角形中,已知一个锐角是
20°,另一个锐角是( )°。
(2)三角形内角和等于( )°。
(3)等边三角形的每个角都是( )°。
(4)如果一个等腰三角形的底角是45°,它
的顶角是( )°,它又是一个( )
三角形。701806090直角(1)一个三角形中,最多只能有一个直角或
钝角。 ( )
(2)在锐角三角形中,任意的两个锐角之和
一定大于90°。 ( )
(3)三角形的三个内角的和的大小与三角
形的大小无关,都是180°。 ( )2.(易错题)判断题。(对的打“√”,错的打“?”)
√√√3.(变式题)选择题。(1)在下面三组角的度数中,不可能是一个三
角形的一组内角的是( )。
A.85°65°30° B.110°30°45°
C.90°65°25°
(2)用一个可以把物体放大10倍的放大镜看
一个三角形,这个三角形的内角和是( )。
A.1800° B.360° C.180°
(3)一个等腰三角形中,有一个角是90°,它的
另外两个内角分别是( )。
A.35°和55° B.45°和45° C.90°和40°BCB4.(难点题)求下列三角形中未知角的度数。90°-25°=65°180°-62°-54°=64°180°-35°×2=110°5.(探究题)求出下面多边形的内角和。 180°×2=360°6.(开放题)一个等腰三角形,它的一个
内角是66°,它的另外两个内角是多
少度?180°-66°×2=48°答:另外两个内角分别为48°、66°。方
法
一(180°-66°)÷2=57°答:另外两个内角都是57°。方
法
二
(1)三角形的内角和是( )。
(2)三角形按边分可分为( )、
( )。三角形按角分可分为
( )、( )和( )。180°等边三角形不等边三角形锐角三角形直角三角形钝角三角形学 习 新 知 早在300多年前就有一位伟大的数学家用科学的数学方法见证了任意三角形的内角和都是180度。这位伟大的数学家就是帕斯卡,他是法国著名的数学家、物理学家。他在12岁时发现了三角形内角和定律。猜一猜,可能是什么三角形?180°-60°-40°=80°锐角三角形你还能猜出是什么三角形?5.它们说的对吗?教材第26页“练一练”第5题。钝角三角形说得不对,钝角三角形两个锐角之和小于90°。直角三角形说得对。6.填出下面各角的度数。教材第26页“练一练”第6题。77°55°115°1.我们可以根据三角形内角和的性质,求出三角形中的未知角的度数。2.我们知道等腰三角形的一个顶角度数,就可以求出一个底角的度数。3.我们可以根据一个或者两个角的度数,推测出三角形的类型。让我仔细想一想!教材第26页“练一练”第7题。 7.挑战自我:探索四边形内角和。1.(基础题)填一填。(1)在一个直角三角形中,已知一个锐角是
20°,另一个锐角是( )°。
(2)三角形内角和等于( )°。
(3)等边三角形的每个角都是( )°。
(4)如果一个等腰三角形的底角是45°,它
的顶角是( )°,它又是一个( )
三角形。701806090直角(1)一个三角形中,最多只能有一个直角或
钝角。 ( )
(2)在锐角三角形中,任意的两个锐角之和
一定大于90°。 ( )
(3)三角形的三个内角的和的大小与三角
形的大小无关,都是180°。 ( )2.(易错题)判断题。(对的打“√”,错的打“?”)
√√√3.(变式题)选择题。(1)在下面三组角的度数中,不可能是一个三
角形的一组内角的是( )。
A.85°65°30° B.110°30°45°
C.90°65°25°
(2)用一个可以把物体放大10倍的放大镜看
一个三角形,这个三角形的内角和是( )。
A.1800° B.360° C.180°
(3)一个等腰三角形中,有一个角是90°,它的
另外两个内角分别是( )。
A.35°和55° B.45°和45° C.90°和40°BCB4.(难点题)求下列三角形中未知角的度数。90°-25°=65°180°-62°-54°=64°180°-35°×2=110°5.(探究题)求出下面多边形的内角和。 180°×2=360°6.(开放题)一个等腰三角形,它的一个
内角是66°,它的另外两个内角是多
少度?180°-66°×2=48°答:另外两个内角分别为48°、66°。方
法
一(180°-66°)÷2=57°答:另外两个内角都是57°。方
法
二
