2018年高中数学第二章圆锥曲线与方程2.1.1曲线与方程的概念课件2新人教B版选修2_1(14张)
文档属性
| 名称 | 2018年高中数学第二章圆锥曲线与方程2.1.1曲线与方程的概念课件2新人教B版选修2_1(14张) |  | |
| 格式 | zip | ||
| 文件大小 | 901.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-11-24 22:24:55 | ||
图片预览





文档简介
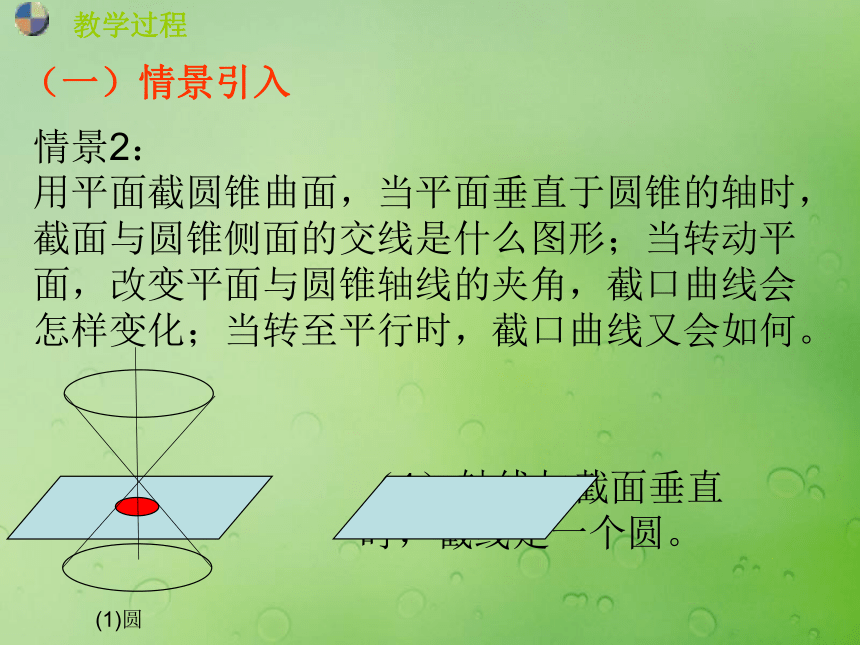
课件14张PPT。2.1.1曲线与方程的概念 教学过程(一)情景引入(1)观察章前图,询问学生图中卫星的运动轨迹;(1)(2)(3)(2)篮球运动员投篮时,球的运动轨迹;(3)电厂冷却塔的外形线分别是什么图形。情景1:(1)轴线与截面垂直时,截线是一个圆。 教学过程(一)情景引入情景2:
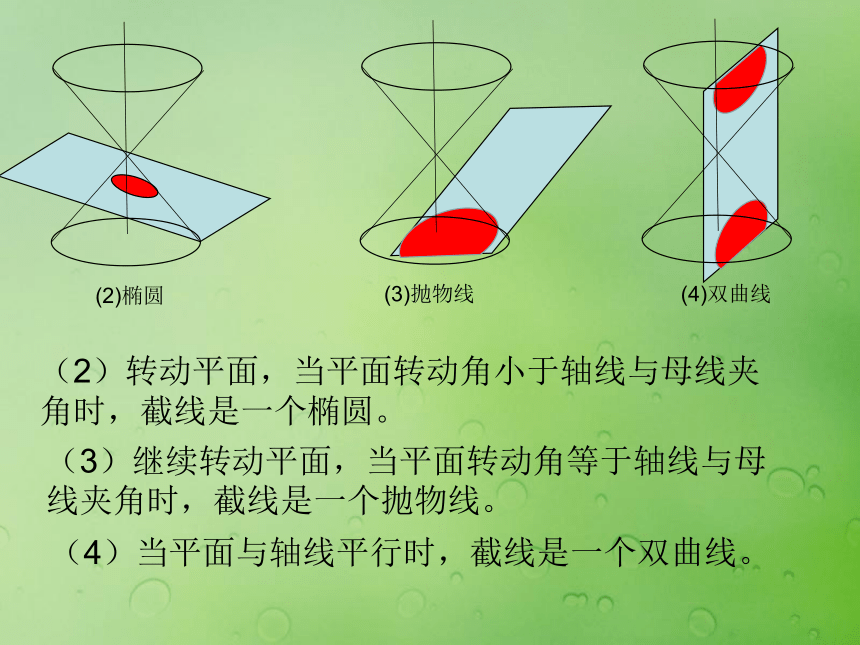
用平面截圆锥曲面,当平面垂直于圆锥的轴时,截面与圆锥侧面的交线是什么图形;当转动平面,改变平面与圆锥轴线的夹角,截口曲线会怎样变化;当转至平行时,截口曲线又会如何。(1)圆(2)椭圆(3)抛物线(4)双曲线(2)转动平面,当平面转动角小于轴线与母线夹角时,截线是一个椭圆。(3)继续转动平面,当平面转动角等于轴线与母
线夹角时,截线是一个抛物线。(4)当平面与轴线平行时,截线是一个双曲线。 教学过程(二)以旧带新 提炼新知1.首先明确下列两个基础问题:
(1)圆的几何定义是什么?
(2)圆的标准方程是什么?回答:
(1)圆的几何概念:平面上到定点的距离等于定长的所有点组成的图形叫做圆。
(2)圆心在原点的圆的标准方程 ①;2.思考能否用方程①来具体刻画圆 O 中的这种几何关系,反过来又是否可以用圆O中的几何关系描述方程①,以下列四个问题为导向:(1)如果直角坐标系中的一点 是圆O上的任意一点,那么 应该满足怎样的条件呢?回答:点 满足 ,整理得: ,即满足方程①。(2)如果直角坐标系中的一点 不是圆O上的一点,那么 一定不满足方程①吗?回答:点 满足 ,整理得: ,即不满足方程①。(3)如果 是方程①的解,那么以 为坐标的点 一定在圆O上吗?
回答: 满足方程①,即 ,整理得 ,所以点 一定在圆O上。 (4)如果 不是方程①的解,那么以 为坐标的点 一定不在圆O上吗?回答: 不满足方程①,即 ,整理得 ,所以点 一定不在圆O上。结论①:圆O上的点的坐标都是方程①的解
结论②:不在圆O 上的点的坐标都不是方程①的解
结论③:以方程①的解为坐标的点都在圆O上
结论④:不以方程①的解为坐标的点都不在圆O上3.将结论推广至一般的圆锥曲线。根据圆与方程的关系,推广可得到曲线上的点与某个方程的解之间是一一对应的关系。从而得出本节课的研究结果,曲线与方程的关系:
(1)曲线上的点的坐标都是这个方程的解;
(2)以方程 的解为坐标的点都是曲线上的点;
这个方程叫做曲线的方程,这条曲线叫做方程的曲线。(二)课堂练习应用举例练习1.点P 是否在方程为 圆上,是否在方程为 的直线l上?答:点P 既在直线上又在圆上。练习2.A. 充分不必要条件 B. 必要不充分条件
C. 充要条件 D.既不充分也不必要条件练习3:已知两圆C1: ,C2: ,求两圆交点。答:联立方程求两曲线交点坐标 和 。 已知两条曲线C1和C2的方程分别为F(x,y)=0,G(x,y)=0,则交点的坐标必须满足上面两个方程,反之如果(x0, y0)是上面两个方程的公共解,则以(x0, y0)为坐标的点必定是两条曲线的交点。因此求两条曲线C1和C2的交点坐标,只要求方程组
的实数解就可以得到。例1. 已知两圆C1:x2+y2+6x-16=0,C2:x2+y2-4x-5=0, 判断:对任意不等于-1的实数λ,方程x2+y2+6x-16+λ(x2+y2-4x-5)=0表示什么曲线?解:方程x2+y2+6x-16+λ(x2+y2-4x-5)=0可以变形为
(1+λ)x2+(1+λ)y2+(6-4λ)x-16-5λ=0,因为λ≠-1,得 因为方程中等号右端大于0,所以它是一个圆的方程,两圆的交点坐标满足已知圆的方程,当然也满足这个方程。因此此方程表示的圆通过两圆交点。思考与讨论:下面命题正确吗?如图,MA和MB分别是动点M(x,y)与两定点A(-1,0),B(1,0)的连线,使∠AMB为直角的动点轨迹方程是:x2+y2=1.
用平面截圆锥曲面,当平面垂直于圆锥的轴时,截面与圆锥侧面的交线是什么图形;当转动平面,改变平面与圆锥轴线的夹角,截口曲线会怎样变化;当转至平行时,截口曲线又会如何。(1)圆(2)椭圆(3)抛物线(4)双曲线(2)转动平面,当平面转动角小于轴线与母线夹角时,截线是一个椭圆。(3)继续转动平面,当平面转动角等于轴线与母
线夹角时,截线是一个抛物线。(4)当平面与轴线平行时,截线是一个双曲线。 教学过程(二)以旧带新 提炼新知1.首先明确下列两个基础问题:
(1)圆的几何定义是什么?
(2)圆的标准方程是什么?回答:
(1)圆的几何概念:平面上到定点的距离等于定长的所有点组成的图形叫做圆。
(2)圆心在原点的圆的标准方程 ①;2.思考能否用方程①来具体刻画圆 O 中的这种几何关系,反过来又是否可以用圆O中的几何关系描述方程①,以下列四个问题为导向:(1)如果直角坐标系中的一点 是圆O上的任意一点,那么 应该满足怎样的条件呢?回答:点 满足 ,整理得: ,即满足方程①。(2)如果直角坐标系中的一点 不是圆O上的一点,那么 一定不满足方程①吗?回答:点 满足 ,整理得: ,即不满足方程①。(3)如果 是方程①的解,那么以 为坐标的点 一定在圆O上吗?
回答: 满足方程①,即 ,整理得 ,所以点 一定在圆O上。 (4)如果 不是方程①的解,那么以 为坐标的点 一定不在圆O上吗?回答: 不满足方程①,即 ,整理得 ,所以点 一定不在圆O上。结论①:圆O上的点的坐标都是方程①的解
结论②:不在圆O 上的点的坐标都不是方程①的解
结论③:以方程①的解为坐标的点都在圆O上
结论④:不以方程①的解为坐标的点都不在圆O上3.将结论推广至一般的圆锥曲线。根据圆与方程的关系,推广可得到曲线上的点与某个方程的解之间是一一对应的关系。从而得出本节课的研究结果,曲线与方程的关系:
(1)曲线上的点的坐标都是这个方程的解;
(2)以方程 的解为坐标的点都是曲线上的点;
这个方程叫做曲线的方程,这条曲线叫做方程的曲线。(二)课堂练习应用举例练习1.点P 是否在方程为 圆上,是否在方程为 的直线l上?答:点P 既在直线上又在圆上。练习2.A. 充分不必要条件 B. 必要不充分条件
C. 充要条件 D.既不充分也不必要条件练习3:已知两圆C1: ,C2: ,求两圆交点。答:联立方程求两曲线交点坐标 和 。 已知两条曲线C1和C2的方程分别为F(x,y)=0,G(x,y)=0,则交点的坐标必须满足上面两个方程,反之如果(x0, y0)是上面两个方程的公共解,则以(x0, y0)为坐标的点必定是两条曲线的交点。因此求两条曲线C1和C2的交点坐标,只要求方程组
的实数解就可以得到。例1. 已知两圆C1:x2+y2+6x-16=0,C2:x2+y2-4x-5=0, 判断:对任意不等于-1的实数λ,方程x2+y2+6x-16+λ(x2+y2-4x-5)=0表示什么曲线?解:方程x2+y2+6x-16+λ(x2+y2-4x-5)=0可以变形为
(1+λ)x2+(1+λ)y2+(6-4λ)x-16-5λ=0,因为λ≠-1,得 因为方程中等号右端大于0,所以它是一个圆的方程,两圆的交点坐标满足已知圆的方程,当然也满足这个方程。因此此方程表示的圆通过两圆交点。思考与讨论:下面命题正确吗?如图,MA和MB分别是动点M(x,y)与两定点A(-1,0),B(1,0)的连线,使∠AMB为直角的动点轨迹方程是:x2+y2=1.
