2014-2018年高考全国卷 文科数学(新课标Ⅰ卷)五年真题(含答案)
文档属性
| 名称 | 2014-2018年高考全国卷 文科数学(新课标Ⅰ卷)五年真题(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-02-13 17:02:55 | ||
图片预览




文档简介
2014年普通高等学校招生全国统一考试
数学文科(新课标Ⅰ卷)一、
选择题:本大题共12小题,每小题5分,
在每小题给出的四个选项中,只有一项是符合题目要求的.
1.
已知集合M={x|-1
A.
(-2,1)
B.
(-1,1)
C.
(1,3)
D.
(-2,3)
2.
若tan
α>0,则( )
A.
sin
α>0
B.
cos
α>0
C.
sin
2α>0
D.
cos
2α>0
3.
设复数z=+i(i为虚数单位),则|z|等于( )
A.
B.
C.
D.
2
4.
已知双曲线-=1(a>0)的离心率为2,则
a等于( )
A.
2
B.
C.
D.
1
5.
设函数f(x),g(x)的定义域都为R,且f(x)是奇函数,g(x)是偶函数,则下列结论中正确的是( )
A.
f(x)g(x)是偶函数
B.
|f(x)|g(x)是奇函数
C.
f(x)|g(x)|是奇函数
D.
|f(x)g(x)|是奇函数
6.
设D,E,F分别为△ABC的三边BC,CA,AB的中点,则+等于( )
A.
B.
C.
D.
7.
在函数①y=cos|2x|,②y=|cos
x|,③y=cos
,④y=tan中,最小正周期为π的所有函数为( )
A.
①②③
B.
①③④
C.
②④
D.
①③
8.
如图,网格纸的各小格都是正方形,粗实线画出的是一个几何体的三视图,则这个几何体是( )
A.
三棱锥
B.
三棱柱
C.
四棱锥
D.
四棱柱
(第8题)
9.
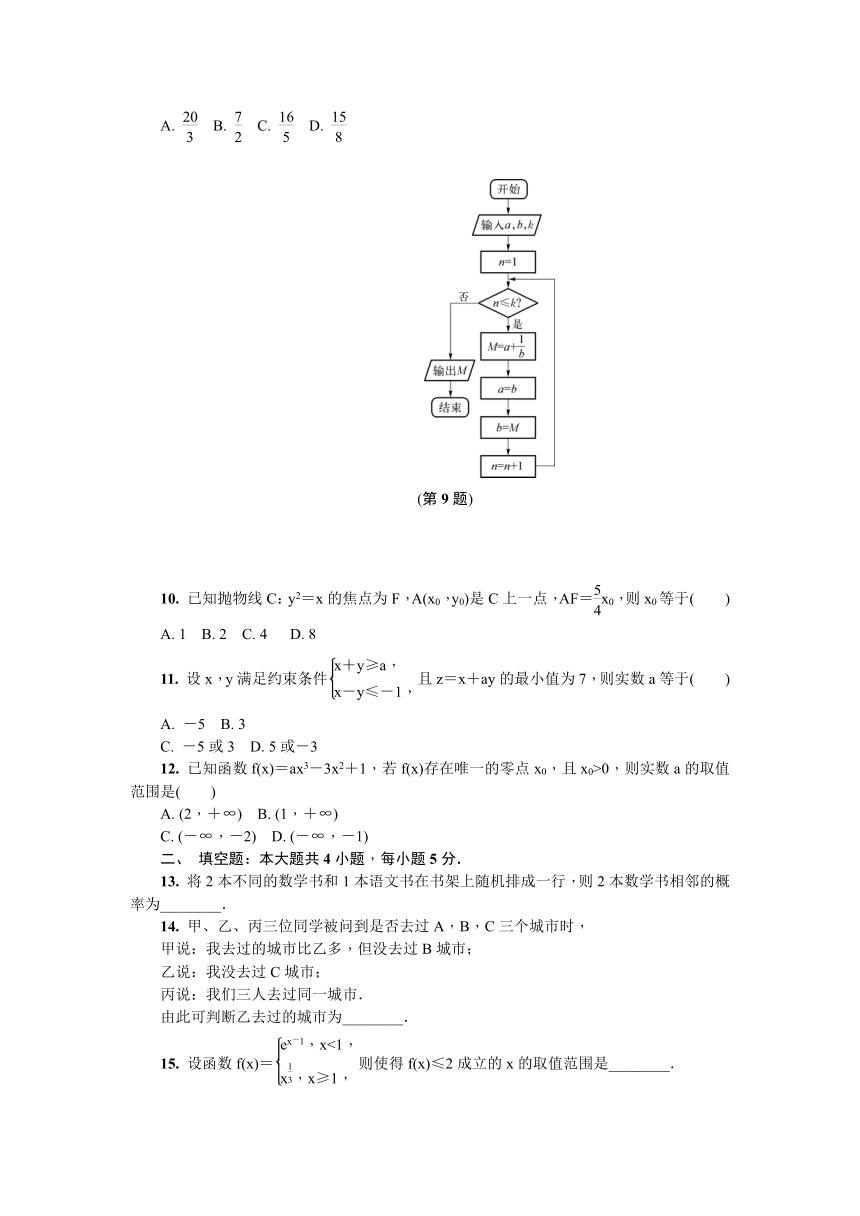
执行如图所示的程序框图,若输入的a,b,k分别为1,2,3,则输出的M等于( )
A.
B.
C.
D.
(第9题)
10.
已知抛物线C:y2=x的焦点为F,A(x0,y0)是C上一点,AF=x0,则x0等于( )
A.
1
B.
2
C.
4
D.
8
11.
设x,y满足约束条件且z=x+ay的最小值为7,则实数a等于( )
A.
-5
B.
3
C.
-5或3
D.
5或-3
12.
已知函数f(x)=ax3-3x2+1,若f(x)存在唯一的零点x0,且x0>0,则实数a的取值范围是( )
A.
(2,+∞)
B.
(1,+∞)
C.
(-∞,-2)
D.
(-∞,-1)
二、
填空题:本大题共4小题,每小题5分.
13.
将2本不同的数学书和1本语文书在书架上随机排成一行,则2本数学书相邻的概率为________.
14.
甲、乙、丙三位同学被问到是否去过A,B,C三个城市时,
甲说:我去过的城市比乙多,但没去过B城市;
乙说:我没去过C城市;
丙说:我们三人去过同一城市.
由此可判断乙去过的城市为________.
15.
设函数f(x)=则使得f(x)≤2成立的x的取值范围是________.
16.
如图,为测量山高MN,选择A和另一座山的山顶C为测量观测点.从点A测得点M的仰角∠MAN=60°,点C的仰角∠CAB=45°以及∠MAC=75°,从点C测得∠MCA=60°.已知山高BC=100m,则山高MN=________m.
(第16题)
三、
解答题:解答应写出文字说明、证明过程或演算步骤.
17.
(本小题满分12分)已知{an}是递增的等差数列,a2,a4是方程x2-5x+6=0的根.
(1)
求数列{an}的通项公式;
(2)
求数列的前n项和.
18.
(本小题满分12分)从某企业生产的某种产品中抽取100件,测量这些产品的一项质量指标值,由测量结果得如下频数分布表:
质量指
标值
分组
[75,85)
[85,95)
[95,105)
[105,115)
[115,125)
频数
6
26
38
22
8
(1)
在下表中作出这些数据的频率分布直方图;
(第18题)
(2)
估计这种产品质量指标值的平均数及方差(同一组中的数据用该组区间的中点值作代表);
(3)
根据以上抽样调查数据,能否认为该企业生产的这种产品符合“质量指标值不低于95的产品至少要占全部产品的80%”的规定?
19.
(本小题满分12分)如图,在三棱柱ABC-A1B1C1中,侧面BB1C1C为菱形,B1C的中点为O,且AO⊥平面BB1C1C.
(1)
求证:B1C⊥AB;
(2)
若AC⊥AB1,∠CBB1=60°,BC=1,求三棱柱ABC-A1B1C1的高.
(第19题)
20.
(本小题满分12分)已知点P(2,2),圆C:x2+y2-8y=0,过点P的动直线l与圆C交于A,B两点,线段AB的中点为M,O为坐标原点.
(1)
求M的轨迹方程;
(2)
当OP=OM时,求l的方程及△POM的面积.
21.
(本小题满分12分)设函数f(x)=aln
x+x2-bx(a≠1),曲线y=f(x)在点(1,f(1))处的切线斜率为0.
(1)
求b;
(2)
若存在x0≥1,使得f(x0)<,求实数a的取值范围.
请考生在第22,23,24题中任选一题作答,如果多做,则按所做的第一题计分.
22.
(本小题满分10分)选修41:几何证明选讲
如图,四边形ABCD是圆O的内接四边形,AB的延长线与DC的延长线交于点E,且CB=CE.
(1)
求证:∠D=∠E;
(2)
设AD不是圆O的直径,AD的中点为M,且MB=MC,求证:△ADE为等边三角形.
(第22题)
23.
(本小题满分10分)选修44:坐标系与参数方程
已知曲线C:+=1,直线l:(t为参数).
(1)
写出曲线C的参数方程与直线l的普通方程;
(2)
过曲线C上任意一点P作与l夹角为30°的直线,交l于点A,求PA的最大值与最小值.
24.
(本小题满分10分)选修45:不等式选讲
若a>0,b>0,且+=.
(1)
求a3+b3的最小值;
(2)
是否存在a,b,使得2a+3b=6?并说明理由.
2014年普通高等学校招生全国统一考试 数学文科(新课标Ⅰ卷)
1.
B 【解析】借助数轴可得M∩N=(-1,1),故选B.
2.
C 【解析】由tan
α>0,可得α的终边在第一象限或第三象限,此时sin
α与cos
α同号,故sin
2α=2sin
αcos
α>0,故选C.
3.
B 【解析】+i=+i=+i=+i,则|z|==,故选B.
4.
D 【解析】因为双曲线的方程为-=1,所以e2==4,因此a2=1,a=1,故选D.
5.
C 【解析】因为f(x)为奇函数,g(x)为偶函数,故f(x)g(x)为奇函数,|f(x)|g(x)为偶函数,f(x)|g(x)|为奇函数,|f(x)g(x)|为偶函数,故选C.
6.
A 【解析】+=(+)+(+)=(+)=,故选A.
7.
A 【解析】①y=cos|2x|的最小正周期为π;②y=|cos
x|的最小正周期为π;③y=cos的最小正周期为π;④y=tan(2x-)的最小正周期为,故选A.
8.
B 【解析】由题意知,该几何体的三视图为一个三角形和两个四边形,经分析可知该几何体为三棱柱,故选B.
9.
D 【解析】第一次循环:M=,a=2,b=,n=2;第二次循环:M=,a=,b=,n=3;第三次循环:M=,a=,b=,n=4,则输出M=,故选D.
10.
A 【解析】由题意知抛物线的准线方程为x=-.因为AF=x0,根据抛物线的定义可得x0+=AF=x0,解得x0=1,故选A.
11.
B 【解析】当a≥1时,联立方程组解得代入x+ay=7中,解得a=3或a=-5(舍去).当a<1时,不符合条件,故选B.
12.
C 【解析】由题意知f′(x)=3ax2-6x=3x(ax-2),当a=0时,不满足题意.当a≠0时,令f′(x)=0,解得x=0或x=.当a>0时,f(x)在(-∞,0),上单调递增,在上单调递减.又f(0)=1,此时f(x)在(-∞,0)上存在零点,不满足题意;当a<0时,f(x)在,(0,+∞)上单调递减,在上单调递增,要使f(x)存在唯一的零点x0,且x0>0,则需f>0,即a×-3×+1>0,解得a<-2,故选C.
13.
【解析】设2本数学书分别为A,B,语文书为C,则所有的排放顺序有ABC,ACB,BAC,BCA,CAB,CBA,共6种情况,其中数学书相邻的有ABC,BAC,CAB,CBA,共4种情况,故2本数学书相邻的概率P==.
14.
A 【解析】根据甲和丙的回答推测乙没去过B城市,又知乙没去过C城市,故乙去过A城市.
15.
(-∞,8] 【解析】当x<1时,由ex-1≤2,得x≤1+ln
2,所以x<1;当x≥1时,由x≤2,得x≤8,所以1≤x≤8.综上,符合题意的x的取值范围是{x|x≤8}.
16.
150 【解析】在△ABC中,AC=100m,在△MAC中,=,解得MA=100m,在△MNA中,MN=MAsin
60°=150(m).
17.
(1)
方程x2-5x+6=0的两根为2,3,由题意得a2=2,a4=3.设数列{an}的公差为d,则a4-a2=2d,故d=,从而a1=,
所以数列{an}的通项公式为an=n+1.
(2)
设的前n项和为Sn,由(1)知=,则
Sn=++…++,
Sn=++…++.
两式相减得
Sn=+-
=+-.
所以Sn=2-.
18.
(1)
(第18题)
(2)
质量指标值的样本平均数为
=80×0.06+90×0.26+100×0.38+110×0.22+120×0.08=100.
质量指标值的样本方差为
s2=(-20)2×0.06+(-10)2×0.26+0×0.38+102×0.22+202×0.08=104.
所以这种产品质量指标值的平均数的估计值为100,方差的估计值为104.
(3)
质量指标值不低于95的产品所占比例的估计值为
0.38+0.22+0.08=0.68.
由于该估计值小于0.8,故不能认为该企业生产的这种产品符合“质量指标值不低于95的产品至少要占全部产品80%”的规定.
19.
(1)
如图,连接BC1,则O为B1C与BC1的交点.
因为侧面BB1C1C为菱形,所以B1C⊥BC1.
又AO⊥平面BB1C1C,所以B1C⊥AO,故B1C⊥平面ABO.
由于AB平面ABO,故B1C⊥AB.
(2)
如图,作OD⊥BC,垂足为D,连接AD.作OH⊥AD,垂足为H.由于BC⊥AO,BC⊥OD,故BC⊥平面AOD,所以OH⊥BC.
(第19题)
又OH⊥AD,所以OH⊥平面ABC.
因为∠CBB1=60°,所以△CBB1为等边三角形.
又BC=1,可得OD=.
由于AC⊥AB1,所以OA=B1C=.
由OH·AD=OD·OA,且AD==,
得OH=.
又O为B1C的中点,所以点B1到平面ABC的距离为,
故三棱柱ABC-A1B1C1的高为.
20.
(1)
圆C的方程可化为x2+(y-4)2=16,所以圆心为C(0,4),半径为4.
设M(x,y),则=(x,y-4),=(2-x,2-y).由题设知·=0,故x(2-x)+(y-4)(2-y)=0,即(x-1)2+(y-3)2=2.
由于点P在圆C的内部,所以M的轨迹方程是(x-1)2+(y-3)2=2.
(2)
由(1)可知M的轨迹是以点N(1,3)为圆心、为半径的圆.
由于OP=OM,故O在线段PM的垂直平分线上.
又P在圆N上,从而ON⊥PM.
因为ON的斜率为3,所以直线l的斜率为-,
故直线l的方程为y=-x+.
又OM=OP=2,O到l的距离为,PM=,
所以△POM的面积为.
21.
(1)
f′(x)=+(1-a)x-b.
由题设知f′(1)=0,解得b=1.
(2)
f(x)的定义域为(0,+∞),由(1)知,f(x)=aln
x+x2-x,
f′(x)=+(1-a)x-1=(x-1).
①若a≤,则≤1,故当x∈(1,+∞)时,f′(x)>0,f(x)在(1,+∞)上单调递增.
所以存在x0≥1,使得f(x0)<的充要条件为f(1)<,即-1<,解得--1②若1,故当x∈时,f′(x)<0;当x∈时,f′(x)>0,所以f(x)在上单调递减,在上单调递增,所以存在x0≥1,使得f(x0)<的充要条件为f<.又f=aln++>,所以不合题意.
③若a>1,则f(1)=-1=<恒成立.
综上,实数a的取值范围是(--1,-1)∪(1,+∞).
22.
(1)
由题设知A,B,C,D四点共圆,
所以∠D=∠CBE.
因为CB=CE,
所以∠CBE=∠E,故∠D=∠E.
(2)
如图,取BC的中点N,连接MN,由MB=MC,
知MN⊥BC,故O在直线MN上.
(第22题)
又AD不是圆O的直径,M为AD的中点,
故OM⊥AD,即MN⊥AD,
所以AD∥BC,故∠A=∠CBE.
又∠CBE=∠E,故∠A=∠E.
由(1)知∠D=∠E,所以△ADE为等边三角形.
23.
(1)
曲线C的参数方程为(θ为参数).
直线l的普通方程为2x+y-6=0.
(2)
曲线C上任意一点P(2cos
θ,3sin
θ)到直线l的距离为
d=|4cos
θ+3sin
θ-6|.
则PA==|5sin(θ+α)-6|,其中α为锐角,且tan
α=.
当sin(θ+α)=-1时,PA取得最大值,最大值为.
当sin(θ+α)=1时,PA取得最小值,最小值为.
24.
(1)
由=+≥,得ab≥2,当且仅当a=b=时等号成立.
故a3+b3≥2≥4,当且仅当a=b=时等号成立.
所以a3+b3的最小值为4.
(2)
由(1)知2a+3b≥2·≥4.
由于4>6,从而不存在a,b,使得2a+3b=6.
2015年普通高等学校招生全国统一考试
数学文科(新课标Ⅰ卷)
一、
选择题:本大题共12小题,每小题5分,
在每小题给出的四个选项中,只有一项是符合题目要求的.
1.
已知集合A={x|x=3n+2,n∈N},B={6,8,10,12,14},则集合A∩B中的元素个数为( )
A.
5
B.
4
C.
3
D.
2
2.
已知点A(0,1),B(3,2),向量=(-4,-3),则向量等于( )
A.
(-7,-4)
B.
(7,4)
C.
(-1,4)
D.
(1,4)
3.
已知复数z满足(z-1)i=1+i,则z等于( )
A.
-2-i
B.
-2+i
C.
2-i
D.
2+i
4.
如果3个正整数可作为一个直角三角形三条边的边长,则称这3个数为一组勾股数,从1,2,3,4,5中任取3个不同的数,则这3个数构成一组勾股数的概率为( )
A.
B.
C.
D.
已知椭圆E的中心在坐标原点,离心率为,E的右焦点与抛物线C:y2=8x的焦点重合,A,B是C的准线与E的两个交点,则AB等于( )
3
B.
6
C.
9
D.
12
6.
《九章算术》是我国古代内容极为丰富的数学名著,书中有如下问题:“今有委米依垣内角,下周八尺,高五尺,问:积及为米几何?”其意思为:“在屋内墙角处堆放米(如图,米堆为一个圆锥的四分之一),米堆底部的弧长为8尺,米堆的高为5尺,问米堆的体积和堆放的米各为多少?”已知1斛米的体积约为1.62立方尺,圆周率约为3,估算出堆放的米约有( )
A.
14斛
B.
22斛
C.
36斛
D.
66斛
(第6题)
7.
已知{an}是公差为1的等差数列,Sn为{an}的前n项和,若S8=4S4,则a10的值为( )
A.
B.
C.
10
D.
12
8.
已知函数f(x)=cos(ωx+φ)的部分图象如图所示,则f(x)的单调减区间为( )
A.
,k∈Z
B.
,k∈Z
C.
,k∈Z
D.
,k∈Z
(第8题)
9.
执行如图所示的程序框图,若输入的t=0.01,则输出的n等于( )
A.
5
B.
6
C.
7
D.
8
(第9题
10.
已知函数f(x)=且f(a)=-3,则f(6-a)等于( )
A.
-
B.
-
C.
-
D.
-
11.
圆柱被一个平面截去一部分后与半球(半径为r)组成一个几何体,该几何体的三视图中的正视图和俯视图如图所示,若该几何体的表面积为16+20π,则r等于( )
A.
1
B.
2
C.
4
D.
8
(第11题)
12.
设函数y=f(x)的图象与y=2x+a的图象关于直线y=-x对称,且f(-2)+f(-4)=1,则a等于( )
A.
-1
B.
1
C.
2
D.
4
二、
填空题:本大题共4小题,每小题5分.
13.
在数列{an}中,a1=2,an+1=2an,Sn为{an}的前n项和,若Sn=126,则n=________.
14.
已知函数f(x)=ax3+x+1的图象在点(1,f(1))处的切线过点(2,7),则实数a=________.
15.
若变量x,y满足约束条件则z=3x+y的最大值为________.
16.
已知F是双曲线C:x2-=1的右焦点,P是C左支上一点,A(0,6),当△APF周长最小时,该三角形的面积为________.
三、
解答题:解答应写出文字说明、证明过程或演算步骤.
17.
(本小题满分12分)已知a,b,c分别是△ABC内角A,B,C的对边,sin2B=
2sin
Asin
C.
(1)
若a=b,求cos
B的值;
(2)
若角B=90°,且a=,求△ABC的面积.
18.
(本小题满分12分)如图,四边形ABCD为菱形,G为AC与BD的交点,BE⊥平面ABCD.
(1)
求证:平面AEC⊥平面BED;
(2)
若∠ABC=120°,AE⊥EC,三棱锥E-ACD的体积为,求该三棱锥的侧面积.
(第18题)
19.
(本小题满分12分)某公司为确定下一年度投入某种产品的宣传费,需了解年宣传费x(单位:千元)对年销售量y(单位:t)和年利润z(单位:千元)的影响,对近8年的宣传费xi和年销售量yi(i=1,2,…,8)的数据作了初步处理,得到如图所示的散点图及一些统计量的值.
(第19题)
(1)
根据散点图判断y=a+bx与y=c+d
哪一个适宜作为年销售量y关于年宣传费x的回归方程类型;(给出判断即可,不必说明理由)
(2)
根据(1)的判断结果及表中数据,建立y关于x的回归方程;
(3)
已知这种产品的年利润z与x,y的关系为z=0.2y-x,根据(2)的结果回答下列问题:
①当年宣传费x=49时,年销售量及年利润的预报值是多少?
②当年宣传费x为何值时,年利润的预报值最大?
附:对于一组数据(u1,v1),(u2,v2),…,(un,vn),其回归直线v=α+βu的斜率和截距的最小二乘估计分别为
=,=v-u.
20.
(本小题满分12分)已知过点A(0,1)且斜率为k的直线l与圆C:(x-2)2+(y-3)2=1交于M,N两点.
(1)
求斜率k的取值范围;
(2)
若·=12,其中O为坐标原点,求MN.
21.
(本小题满分12分)设函数f(x)=e2x-aln
x.
(1)
讨论f(x)的导函数f′(x)的零点的个数;
(2)
求证:当a>0时,f(x)≥2a+aln
.
请考生在第22,23,24题中任选一题作答,如果多做,则按所做的第一题计分.
22.
(本小题满分10分)选修41:几何证明选讲
如图,AB是圆O的直径,AC是圆O的切线,BC交圆O于点E.
(1)
若D为AC中点,求证:DE是圆O的切线;
(2)
若OA=CE,求∠ACB的大小.
(第22题)
23.
(本小题满分10分)选修44:坐标系与参数方程
在平面直角坐标系xOy中,直线C1:x=-2,圆C2:(x-1)2+(y-2)2=1,以坐标原点为极点,x轴正半轴为极轴建立极坐标系.
(1)
求C1,C2的极坐标方程.
(2)
若直线C3的极坐标方程为θ=(ρ∈R),设C2,C3的交点为M,N,求△C2MN的面积.
24.
(本小题满分10分)选修45:不等式选讲
已知函数f(x)=|x+1|-2|x-a|,a>0.
(1)
当a=1时,求不等式f(x)>1的解集;
(2)
若f(x)的图象与x轴围成的三角形面积大于6,求实数a的取值范围.
2015年普通高等学校招生全国统一考试
数学文科(新课标Ⅰ卷)
1.
D 【解析】因为A={x|x=3n+2,n∈N}={…,2,5,8,11,14,…},所以A∩B={8,14},集合A∩B中的元素个数为2.
2.
A 【解析】设C(x,y),因为=(x,y-1)=(-4,-3),所以所以
C(-4,-2),所以=(-4-3,-2-2)=(-7,-4).
3.
C 【解析】设z=x+yi,因为(z-1)i=[(x-1)+yi]i=-y+(x-1)i=1+i,所以所以z=2-i.
4.
C 【解析】因为从1,2,3,4,5中任取3个不同的数共有10种情况,又构成一组勾股数的情况有1种(3,4,5),所以所求概率为.
5.
B 【解析】设椭圆E的标准方程为+=1,依题意得=,c=2,解得a=4,所以b2=12,所以椭圆E的标准方程为+=1,令x=-2,解得y=±3,所以AB=3-
(-3)=6.
6.
B 【解析】由题意可知米堆的下底面圆半径为r==,所以米堆的体积为V=×Sh=××3××5=,所以估算出堆放的米约有≈21.94≈22(斛).
7.
B 【解析】由S8=4S4,得=4×,化简得a8=a1+2a4,又d=1,可求得a1=,所以a10=a1+9d=+9=.
8.
D 【解析】由图可知,T=-=1,所以T=2=,从而ω=π.由f=cos=0及图象的单调性,可知φ=.令2kπ<πx+<π+2kπ,k∈Z,解得2k-9.
C 【解析】第一次循环:S=,m=,n=1;第二次循环:S=,m=,n=2;
第三次循环:S=,m=,n=3;第四次循环:S=,m=,n=4;
第五次循环:S=,m=,n=5;第六次循环:S=,m=,n=6;
第七次循环:S=,m=,n=7.此时S=<0.01,循环结束.
10.
A 【解析】当a≤1时,由2a-1-2=-3,知a无解;
当a>1时,由-log2(a+1)=-3,解得a=7,
所以f(6-a)=f(6-7)=f(-1)=2-1-1-2=-2=-.
11.
B 【解析】该几何体由一个半球和半个圆柱组成,圆柱的高为2r,底面半径和球的半径均为r,组合体的表面积为S=2×πr2+πr×2r+2r×2r+×4πr2=5πr2+4r2=16+20π,所以r2=4,r=2.
12.
C 【解析】依题意得-x=2-y+a,即f(x)=-log2(-x)+a.
因为f(-2)+f(-4)=1,所以-log22+a-log24+a=1,
即2a=1+1+2=4,所以a=2.
13.
6 【解析】因为an+1=2an,即=2,所以{an}是以2为首项、2为公比的等比数列,因此Sn===126,即2n-1=63,2n=64,所以n=6.
14.
1 【解析】因为f′(x)=3ax2+1,所以斜率k=f′(1)=3a+1.又f(1)=a+2,所以切线方程为y-(a+2)=(3a+1)(x-1),所以7-a-2=(3a+1)×1,所以a=1.
15.
4 【解析】作出不等式组表示的可行域如图中阴影部分所示,由目标函数z=3x+y,得y=-3x+z,显然,当直线y=-3x+z经过点B时,在y轴上的截距最大,即z最大.由解得即B(1,1),所以zmax=3×1+1=4.
(第15题)
16.
12 【解析】如图,设F1为双曲线的左焦点,则AF=15,AF=AF1,C△APF=AP+PF+FA=AP+PF+AF1.因为PF-PF1=2a=2,所以PF=PF1+2,所以C△APF=AP+PF1+2+AF1≥AF1+2+AF1,即A,P,F1三点共线时,△APF的周长最小,为32,此时直线lAF1:y=2(x+3).联立解得x=-2,y=2,所以S△APF=S△AF1F-S△PF1F=×6×6-×6×2=12.
(第16题)
17.
(1)
由题设及正弦定理可得b2=2ac.又a=b,可得b=2c,a=2c.
由余弦定理可得cos
B==.
(2)
由题设知b2=2ac.因为B=90°,由勾股定理得a2+c2=b2,
故a2+c2=2ac,得c=a=,所以△ABC的面积为1.
18.
(1)
因为四边形ABCD为菱形,所以AC⊥BD.
因为BE⊥平面ABCD,AC平面ABCD,所以AC⊥BE.
又因为BE∩BD=B,故AC⊥平面BED.
又AC平面AEC,所以平面AEC⊥平面BED.
设AB=x,在菱形ABCD中,由∠ABC=120°,
可得AG=GC=x,GB=GD=.
因为AE⊥EC,所以在Rt△AEC中,可得EG=x.
由BE⊥平面ABCD,知△EBG为直角三角形,可得BE=x.
由已知得,三棱锥E-ACD的体积VE-ACD=×AC·GD·BE=x3=,故x=2.
从而可得AE=EC=ED=,
所以△EAC的面积为3,△EAD的面积与△ECD的面积均为,
故三棱锥EACD的侧面积为3+2.
19.
(1)
由散点图可以判断,y=c+d适宜作为年销售量y关于年宣传费x的回归方程类型.
(2)
令w=,先建立y关于w的线性回归方程,由于=68,
=y-w=563-68×6.8=100.6,
所以y关于w的线性回归方程为=100.6+68w,
因此y关于x的回归方程为=100.6+68.
(3)
①由(2)知,当x=49时,年销售量y的预报值=100.6+68=576.6,
年利润z的预报值=576.6×0.2-49=66.32.
②根据(2)的结果知,年利润z的预报值=0.2(100.6+68)-x=-x+13.6+20.12.
所以当==6.8,即x=46.24时,取得最大值.
故年宣传费为46.24千元时,年利润的预报值最大.
(1)
由题设可知直线l的方程为y=kx+1.
因为l与C交于两点,所以<1,解得所以斜率k的取值范围为.
(2)
设M(x1,y1),N(x2,y2).将y=kx+1代入方程(x-2)2+(y-3)2=1,
整理得(1+k2)x2-4(1+k)x+7=0,所以x1+x2=,x1x2=.
·=x1x2+y1y2=(1+k2)x1x2+k(x1+x2)+1=+8.
由题设可得+8=12,解得k=1,所以直线l的方程为y=x+1.
故圆心C在l上,所以MN=2.
21.
(1)
f(x)的定义域为(0,+∞),f′(x)=2e2x-(x>0).
当a≤0时,f′(x)>0,f′(x)没有零点;
当a>0时,因为e2x单调递增,-单调递增,所以f′(x)在(0,+∞)上单调递增.
又f′(a)>0,当b满足00时,f′(x)存在唯一零点.
由(1)可设f′(x)在(0,+∞)上的唯一零点为x0,
当x∈(0,x0)时,f′(x)<0;当x∈(x0,+∞)时,f′(x)>0.
故f(x)在(0,x0)上单调递减,在(x0,+∞)上单调递增,
所以当x=x0时,f(x)取得最小值,最小值为f(x0).
由于2e2x0-=0,所以f(x0)=+2ax0+aln
≥2a+aln
.
故当a>0时,f(x)≥2a+aln
.
(1)
如图,连接AE,由已知得,AE⊥BC,AC⊥AB.
在Rt△AEC中,由已知得DE=DC,
故∠DEC=∠DCE.
连接OE,则∠OBE=∠OEB.
又∠ACB+∠ABC=90°,
所以∠DEC+∠OEB=90°,
故∠OED=90°,DE是圆O的切线.
(2)
设CE=1,AE=x,由已知得AB=2,BE=.
由射影定理可得,AE2=CE·BE,
所以x2=,即x4+x2-12=0,
可得x=,所以∠ACB=60°
(第22题)
.
23.
(1)
因为x=ρcos
θ,y=ρsin
θ,所以C1的极坐标方程为ρcos
θ=-2,C2的极坐标方程为ρ2-2ρcos
θ-4ρsin
θ+4=0.
(2)
将θ=代入ρ2-2ρcos
θ-4ρsin
θ+4=0,得ρ2-3ρ+4=0,解得ρ1=2,
ρ2=,故ρ1-ρ2=,即MN=.
由于C2的半径为1,所以△C2MN的面积为.
24.
(1)
当a=1时,f(x)>1可化为|x+1|-2|x-1|-1>0.
当x≤-1时,不等式化为x-4>0,无解;
当-10,解得当x≥1时,不等式化为-x+2>0,解得1≤x<2,
所以f(x)>1的解集为.
(2)
由题设可得,f(x)=
所以函数f(x)的图象与x轴围成的三角形的三个顶点分别为A,B(2a+1,0),C(a,a+1),△ABC的面积为(a+1)2.
由题设得(a+1)2>6,故a>2.
所以实数a的取值范围为(2,+∞).
2016年普通高等学校招生全国统一考试
数学文科(新课标Ⅰ卷)
一、
选择题:本大题共12小题,每小题5分.
1.
设集合A={1,3,5,7},B={x|2≤x≤5},则A∩B等于( )
A.
{1,3}
B.
{3,5}
C.
{5,7}
D.
{1,7}
2.
设(1+2i)(a+i)的实部与虚部相等,其中a为实数,则a等于( )
A.
-3
B.
-2
C.
2
D.
3
3.
为美化环境,从红、黄、白、紫4种颜色的花中任选2种花种在一个花坛中,余下的2种花种在另一个花坛中,则红色和紫色的花不在同一花坛的概率是( )
A.
B.
C.
D.
4.
△ABC的内角A,B,C的对边分别为a,b,c.已知a=,c=2,cos
A=,则b等于( )
A.
B.
C.
2
D.
3
5.
直线l经过椭圆的一个顶点和一个焦点,若椭圆中心到l的距离为其短轴长的,则该椭圆的离心率为( )
A.
B.
C.
D.
6.
将函数y=2sin的图象向右平移个周期后,所得图象对应的函数为( )
A.
y=2sin
B.
y=2sin
C.
y=2sin
D.
y=2sin
7.
如图,某几何体的三视图是三个半径相等的圆及每个圆中两条相互垂直的半径.若
(第7题)
该几何体的体积是,则它的表面积是( )
A.
17π
B.
18π
C.
20π
D.
28π
8.
若a>b>0,0A.
logacB.
logcaC.
acD.
ca>cb
9.
函数y=2x2-e|x|在[-2,2]上的图象大致为( )
,
,
(B)
(D)
10.
执行如图所示的程序框图,如果输入的x=0,y=1,n=1,则输出x,y的值满足( )
A.
y=2x
B.
y=3x
C.
y=4x
D.
y=5x
(第10题)
11.
平面α过正方体ABCD-A1B1C1D1的顶点A,α∥平面CB1D1,α∩平面ABCD=m,α∩平面ABB1A1=n,则m,n所成角的正弦值为( )
A.
B.
C.
D.
12.
若函数f(x)=x-sin
2x+asin
x在(-∞,+∞)上单调递增,则a的取值范围是( )
A.
[-1,1]
B.
C.
D.
二、
填空题:本大题共4小题,每小题5分.
13.
设向量a=(x,x+1),b=(1,2),且a⊥b,则x=________.
14.
已知θ是第四象限角,且sin=,则tan=_________.
15.
设直线y=x+2a与圆C:x2+y2-2ay-2=0相交于A,B两点,若AB=2,则圆C的面积为________.
16.
某高科技企业生产产品A和产品B需要甲、乙两种新型材料.生产一件产品A需要甲材料1.5
kg,乙材料1
kg,用5个工时;生产一件产品B需要甲材料0.5
kg,乙材料0.3
kg,用3个工时,生产一件产品A的利润为2
100元,生产一件产品B的利润为900元.该企业现有甲材料150
kg,乙材料90
kg,则在不超过600个工时的条件下,生产产品A、产品B的利润之和的最大值为________元.
三、
解答题:解答时应写出必要的文字说明、证明过程或演算步骤.
17.(本小题满分12分)已知{an}是公差为3的等差数列,数列{bn}满足b1=1,b2=,anbn+1+bn+1=nbn.
(1)
求数列{an}的通项公式;
(2)
求数列{bn}的前n项和.
18.
(本小题满分12分)如图,已知正三棱锥P-ABC的侧面是直角三角形,PA=6,顶点P在平面ABC内的正投影为点D,D在平面PAB内的正投影为点E,连接PE并延长交AB于点G.
(1)
求证:G是AB的中点;
(2)
在图中作出点E在平面PAC内的正投影F(说明作法及理由),并求四面体PDEF的体积.
(第18题)
19.
(本小题满分12分)某公司计划购买1台机器,该种机器使用三年后即被淘汰.机器有一易损零件,在购进机器时,可以额外购买这种零件作为备件,每个200元.在机器使用期间,如果备件不足再购买,则每个500元.现需决策在购买机器时应同时购买几个易损零件,为此搜集并整理了100台这种机器在三年使用期内更换的易损零件数,得到如图所示的柱状图.记x表示1台机器在三年使用期内需更换的易损零件数,y表示1台机器在购买易损零件上所需的费用(单位:元),n表示购机的同时购买的易损零件数.
(1)
若n=19,求y与x的函数解析式;
(2)
若要求“需更换的易损零件数不大于n”的频率不小于0.5,求n的最小值;
(3)
假设这100台机器在购机的同时每台都购买19个易损零件,或每台都购买20个易损零件,分别计算这100台机器在购买易损零件上所需费用的平均数,以此作为决策依据,购买1台机器的同时应购买19个还是20个易损零件?
(第19题)
20.
(本小题满分12分)在直角坐标系xOy中,直线l:y=t(t≠0)交y轴于点M,交抛物线C:y2=2px(p>0)于点P,M关于点P的对称点为N,连接ON并延长交C于点H.
(1)
求;
(2)
除H以外,直线MH与C是否有其他公共点?请说明理由.
21.
(本小题满分12分)已知函数f(x)=(x-2)ex+a(x-1)2.
(1)
讨论f(x)的单调性;
(2)
若f(x)有两个零点,求a的取值范围.
请考生在第22,23,24题中任选一题作答,如果多做,则按所做的第一题计分.
22.
(本小题满分10分)选修41:几何证明选讲
如图,△OAB是等腰三角形,∠AOB=120°.以O为圆心,OA为半径作圆.
(1)
求证:直线AB与圆O相切;
(2)
点C,D在圆O上,且A,B,C,D四点共圆,求证:AB∥CD.
(第22题)
23.
(本小题满分10分)选修44:坐标系与参数方程
在直角坐标系xOy中,曲线C1的参数方程为(t为参数,a>0).在以坐标原点为极点,x轴正半轴为极轴的极坐标系中,曲线C2:ρ=4cos
θ.
(1)
说明C1是哪种曲线,并将C1的方程化为极坐标方程;
(2)
直线C3的极坐标方程为θ=α0,其中α0满足tan
α0=2,若曲线C1与C2的公共点都在C3上,求a.
24.
(本小题满分10分)选修45:不等式选讲
已知函数f(x)=|x+1|-|2x-3|.
(1)
画出y=f(x)的图象;
(2)
求不等式|f(x)|>1的解集.
(第24题)
2016年普通高等学校招生全国统一考试
数学文科(新课标Ⅰ卷)
1.
B 【解析】集合A与集合B的公共元素为3,5,所以A∩B={3,5},故选B.
2.
A 【解析】(1+2i)(a+i)=a-2+(1+2a)i,由已知,得a-2=1+2a,解得a=-3.故选A.
3.
C 【解析】将4种颜色的花种任选两种种在一个花坛中,余下2种种在另一个花坛,有6种种法,其中红色和紫色的花不在一个花坛的种法有4种,故所求概率为.故选C.
4.
D 【解析】由余弦定理得5=b2+4-2×b×2×,解得b=3,b=-(舍去).故选D.
5.
B 【解析】如图,由题意得在椭圆中,OF=c,OB=b,OD=×2b=b,BF=a,在Rt△OFB中,OF×OB=BF×OD,即cb=,所以c=,所以椭圆的离心率e=.故选B.
(第5题)
6.
D 【解析】函数y=2sin的周期为π,将函数y=2sin(2x+)的图象向右平移个周期即个单位长度,得到函数y=2sin[2(x-)+]=2sin的图象.故选D.
7.
A 【解析】由三视图可知该几何体为一个切去了部分的球,设球的半径为r,则×=,解得r=2.此几何体的表面积应为个球面面积加上3个圆面积之和,所以表面积为(4πr2)×+3×=17π.故选A.
8.
B 【解析】对于选项A:logac=,logbc=,因为0c<0,而a>b>0,所以lg
a>lg
b,但不能确定lg
a,lg
b的正负,所以它们的大小不能确定;对于选项B:logca=,logcb=,而lg
a>lg
b,两边同乘以一个负数改变不等号方向,所以选项B正确;对于选项C:利用y=xc在第一象限内是增函数可得ac>bc,所以C错误;对于选项D:利用y=cx在R上为减函数易得D错误.故选B.
9.
D 【解析】函数y=f(x)=2x2-e|x|在[-2,2]上是偶函数,其图象关于y轴对称,因为f(2)=8-e2,0<8-e2<1,所以排除A,B选项;当x∈[0,2]时,y′=4x-ex有一零点,设为x0,当x∈(0,x0)时,f(x)为减函数,当x∈(x0,2)时,f(x)为增函数.故选D.
10.
C 【解析】第一次循环:x=0,y=1,第二次循环:n=2,x=,y=2,第三次循环:n=3,x=,y=6,此时满足条件x2+y2≥36,结束循环,输出x=,y=6,满足y=4x.故选C.
11.
A 【解析】如图,因为α∥平面CB1D1,设平面CB1D1∩平面ABCD=m1,则
m1∥m.又因为平面ABCD∥平面A1B1C1D1,平面B1D1C∩平面A1B1C1D1=B1D1,所以B1D1∥m1,故B1D1∥m.同理可得CD1∥n.故m,n所成角的大小与B1D1,CD1所成角的大小相等,即为∠CD1B1的大小.而B1C=B1D1=CD1(均为面对角线),因此∠CD1B1=,即sin∠CD1B1=.故选A.
(第11题)
12.
C 【解析】用特殊值法:取a=-1,则f(x)=x-sin
2x-sin
x,f′(x)=1-cos
2x-cos
x,因为f′(0)=1--1=-<0,所以f(x)不可能在(-∞,+∞)上单调递增,排除A,B,D.故选C.
13.
- 【解析】由题意知a·b=0,x+2(x+1)=0,所以x=-.
14.
-
【解析】由题意得cos=,则tan=,所以tan=tan(θ+-)=-=-.
15.
4π 【解析】圆C:x2+y2-2ay-2=0,即C:x2+(y-a)2=a2+2,圆心为C(0,a),由AB=2,圆心C到直线y=x+2a的距离为,得+=a2+2,解得a2=2,所以圆C的面积为π(a2+2)=4π.
16.
216
000 【解析】设生产产品A、产品B分别为x,y件,利润之和为z元,目标函数z=2
100x+900y.由题意得即
作出可行域如图中阴影部分所示,
将z=2
100x+900y变形,得y=-x+,平移直线y=-x,当直线y=-x+经过点M时,z
取得最大值.由得点M的坐标为(60,100).所以当x=60,y=100时,zmax=2
100×60+900×100=216
000.经检验,符合题意.
(第16题)
17.
(1)
由已知得a1b2+b2=b1,又b1=1,b2=,得a1=2,
所以数列{an}是首项为2、公差为3的等差数列,
其通项公式为an=3n-1.
由(1)及anbn+1+bn+1=nbn,得bn+1=,
因此{bn}是首项为1、公比为的等比数列,设{bn}的前n项和为Sn,
则Sn==-.
18.
(1)
因为P在平面ABC内的正投影为D,所以AB⊥PD.
因为D在平面PAB内的正投影为E,所以AB⊥DE.
因为DE∩PD=D,所以AB⊥平面PED,故AB⊥PG.
又由已知可得PA=PB,从而G是AB的中点.
(第18题)
(2)
如图,在平面PAB内,过点E作PB的平行线交PA于点F,F即为E在平面PAC内的正投影.
理由如下:由已知可得PB⊥PA,PB⊥PC,又EF∥PB,所以EF⊥PA,EF⊥PC,又PA∩PC=P,所以EF⊥平面PAC,即点F为E在平面PAC内的正投影.
连接CG,因为P在平面ABC内的正投影为D,
所以D是正三角形ABC的中心.
由(1)知G是AB的中点,所以D在CG上,且CD=CG.
由题设可得PC⊥平面PAB,DE⊥平面PAB,
所以DE∥PC,因此PE=PG,DE=PC.
由已知,正三棱锥的侧面是直角三角形且PA=6,
所以DE=2,PE=2.
在等腰直角三角形EFP中,可得EF=PF=2,
所以四面体PDEF的体积V=S△EFP·DE=××2×2×2=.
19.
(1)
当x≤19时,y=3
800;
当x>19时,y=3
800+500(x-19)=500x-5
700.
所以y与x的函数解析式为
y=(x∈N).
(2)
由柱状图知,需更换的零件数不大于18的频率为0.46,不大于19的频率为0.7,故n的最小值为19.
(3)
若每台机器在购机同时都购买19个易损零件,则这100台机器中有70台在购买易损零件上的费用为3
800元,20台的费用为4
300元,10台的费用为4
800元,因此这100台机器在购买易损零件上所需费用的平均数为×(3
800×70+4
300×20+4
800×10)=4
000.
若每台机器在购机同时都购买20个易损零件,则这100台机器中有90台在购买易损零件上的费用为4
000元,10台的费用为4
500元,因此这100台机器在购买易损零件上所需费用的平均数为×(4
000×90+4
500×10)=4
050.
比较两个平均数可知,购买1台机器的同时应购买19个易损零件.
20.
(1)
由已知得M(0,t),P.
又N为M关于点P的对称点,故N,ON的方程为y=x,代入y2=2px,整理得px2-2t2x=0,解得x1=0,x2=,因此H,
所以N为OH的中点,即=2.
(2)
直线MH与C除H以外没有其他公共点,理由如下:
由(1)知直线MH的方程为y-t=x,即x=(y-t).
代入y2=2px得y2-4ty+4t2=0,解得y1=y2=2t,即直线MH与C只有一个公共点,所以除H以外直线MH与C没有其他公共点.
21.
(1)
f′(x)=(x-1)ex+2a(x-1)=(x-1)(ex+2a).
若a≥0,则当x∈(-∞,1)时,f′(x)<0;当x∈(1,+∞)时,f′(x)>0,
所以f(x)在(-∞,1)上单调递减,在(1,+∞)上单调递增.
若a<0,由f′(x)=0,得x=1或x=ln(-2a).
①当a=-时,则f′(x)=(x-1)(ex-e)≥0,
所以f(x)在(-∞,+∞)上单调递增.
②当a>-时,则ln(-2a)<1,故当x∈(-∞,ln(-2a))∪(1,+∞)时,f′(x)>0;当x∈(ln(-2a),1)时,f′(x)<0,所以f(x)在(-∞,ln(-2a)),(1,+∞)上单调递增,在(ln(-2a),1)上单调递减.
③当a<-时,则ln(-2a)>1,故当x∈(-∞,1)∪(ln(-2a),+∞)时,f′(x)>0;当x∈(1,ln(-2a))时,f′(x)<0,
所以f(x)在(-∞,1),(ln(-2a),+∞)上单调递增,在(1,ln(-2a))上单调递减.
(2)
①若a>0,则由(1)知f(x)在(-∞,1)上单调递减,在(1,+∞)上单调递增.
又f(1)=-e,f(2)=a,取b满足b<0且b<ln,
则f(b)>(b-2)+a(b-1)2=a>0,所以f(x)有两个零点.
②若a=0,则f(x)=(x-2)ex,所以f(x)只有一个零点.
③若a<0,当a≥-时,则由(1)知f(x)在(1,+∞)上单调递增,又当x≤1时f(x)<0,故f(x)不存在两个零点;
当a<-时,则由(1)知f(x)在(1,ln(-2a))上单调递减,在(ln(-2a),+∞)上单调递增,又当x≤1时f(x)<0,故f(x)不存在两个零点.
综上,a的取值范围为(0,+∞).
22.
(1)
如图,设E是AB的中点,连接OE.
因为OA=OB,∠AOB=120°,所以OE⊥AB,∠AOE=60°.
在Rt△AOE中,OE=AO,即点O到直线AB的距离等于圆O的半径,
所以直线AB与圆O相切.
(第22题)
(2)
因为OA=2OD,所以O不是A,B,C,D四点所在圆的圆心.
如图,设O′是A,B,C,D四点所在圆的圆心,作直线OO′.
由已知得O在线段AB的垂直平分线上,
又O′在线段AB的垂直平分线上,所以OO′⊥AB.
同理可证OO′⊥CD,所以AB∥CD.
23.
(1)
消去参数t得到C1的普通方程为x2+(y-1)2=a2,
故C1是以(0,1)为圆心,a为半径的圆.
将x=ρcos
θ,y=ρsin
θ代入C1的普通方程中,得C1的极坐标方程为ρ2-2ρsin
θ+1-a2=0.
(2)
曲线C1,C2的公共点的极坐标满足方程组
若ρ≠0,由方程组得16cos2
θ-8sin
θcos
θ+1-a2=0.
由已知tan
θ=2,可得16cos2
θ-8sin
θcos
θ=0,
从而1-a2=0,解得a=-1(舍去)或a=1.
当a=1时,极点为C1,C2的公共点,且在C3上,
所以a=1.
24.
(1)
f(x)=y=f(x)的图象如图所示.
(第24题)
(2)
由|f(x)|>1得f(x)>1或f(x)<-1.当f(x)=1时,可得x=1或x=3;
当f(x)=-1时,可得x=或x=5.
由y=f(x)的图象知f(x)>1的解集为{x|1<x<3},f(x)<-1的解集为.
所以|f(x)|>1的解集为.
2017年普通高等学校招生全国统一考试
数学文科(新课标Ⅰ卷)
一、
选择题:本大题共12小题,每小题5分.
1.
已知集合A={x|x<2},B={x|3-2x>0},那么( )
A.
A∩B=
B.
A∩B=
C.
A∪B=
D.
A∪B=R
2.
为评估一种农作物的种植效果,选了n块地作试验田.这n块地的亩产量(单位:kg)分别为x1,x2,…,xn,下面给出的指标中可以用来评估这种农作物亩产量稳定程度的是( )
A.
x1,x2,…,xn的平均值
B.
x1,x2,…,xn的标准差
C.
x1,x2,…,xn的最大值
D.
x1,x2,…,xn的中位数
3.
下列各式的运算结果为纯虚数的是( )
A.
i(1+i)2
B.
i2(1-i)
C.
(1+i)2
D.
i(1+i)
4.
如图,正方形ABCD内的图形来自中国古代的太极图.正方形内切圆中的黑色部分和白色部分关于正方形的中心成中心对称.若在正方形内随机取一点,则此点取自黑色部分的概率是( )
A.
B.
C.
D.
(第4题)
5.
已知F是双曲线C:x2-=1的右焦点,P是C上一点,且PF与x轴垂直,点A的坐标是(1,3),那么△APF的面积为( )
A.
B.
C.
D.
6.
如图,在下列四个正方体中,若A,B为正方体的两个顶点,M,N,Q为所在棱的中点,则在这四个正方体中,直线AB与平面MNQ不平行的是( )
若x,y满足约束条件则z=x+y的最大值为( )
A.
0
B.
1
C.
2
D.
3
8.
函数y=的部分图象大致为( )
9.
已知函数f(x)=lnx+ln(2-x),那么( )
A.
f(x)在(0,2)上单调递增
B.
f(x)在(0,2)上单调递减
C.
y=f(x)的图象关于直线x=1对称
D.
y=-f(x)的图象关于点(1,0)对称
10.
如图所示的程序框图是为了求出满足3n-2n>1
000的最小偶数n,那么在和两个空白框中,可以分别填入( )
A.
A>1
000和n=n+1
B.
A>1
000和n=n+2
C.
A≤1
000和n=n+1
D.
A≤1
000和n=n+2
(第10题)
11.
已知△ABC的内角A,B,C的对边分别为a,b,c.若sinB+sinA(sinC-cosC)=0,a=2,c=,则角C等于( )
A.
B.
C.
D.
12.
已知A,B是椭圆C:+=1长轴的两个端点.若C上存在点M满足∠AMB=120°,则m的取值范围是( )
A.
(0,1]∪[9,+∞)
B.
(0,]∪[9,+∞)
C.
(0,1]∪[4,+∞)
D.
(0,]∪[4,+∞)
二、
填空题:本大题共4小题,每小题5分.
13.
已知向量a=(-1,2),b=(m,1).若向量a+b与a垂直,则m=________.
14.
曲线y=x2+在点(1,2)处的切线方程为________.
15.
已知α∈,tanα=2,那么cos=________.
16.
已知三棱锥S-ABC的所有顶点都在球O的球面上,SC是球O的直径.若平面SCA⊥平面SCB,SA=AC,SB=BC,三棱锥S-ABC的体积为9,则球O的表面积为________.
三、
解答题:解答时应写出必要的文字说明、证明过程或演算步骤.
17.
(本小题满分12分)记Sn为等比数列{an}的前n项和.已知S2=2,S3=-6.
(1)
求{an}的通项公式;
(2)
求Sn,并判断Sn+1,Sn,Sn+2是否成等差数列.
18.
(本小题满分12分)如图,在四棱锥P-ABCD中,AB∥CD,且∠BAP=∠CDP=90°.
(1)
求证:平面PAB⊥平面PAD;
(2)
若PA=PD=AB=DC,∠APD=90°,且四棱锥P-ABCD的体积为,求该四棱锥的侧面积.
(第18题)
19.
(本小题满分12分)为了监控某种零件的一条生产线的生产过程,检验员每隔30
min从该生产线上随机抽取一个零件,并测量其尺寸(单位:cm).下面是检验员在一天内依次抽取的16个零件的尺寸:
抽取次序
1
2
3
4
5
6
7
8
零件尺寸
9.95
10.12
9.96
9.96
10.01
9.92
9.98
10.04
抽取次序
9
10
11
12
13
14
15
16
零件尺寸
10.26
9.91
10.13
10.02
9.22
10.04
10.05
9.95
(1)
求(xi,i)(i=1,2,…,16)的相关系数r,并回答是否可以认为这一天生产的零件尺寸不随生产过程的进行而系统地变大或变小(若|r|<0.25,则可以认为零件的尺寸不随生产过程的进行而系统地变大或变小).
(2)
在一天内抽检的零件中,如果出现了尺寸在(x-3s,x+3s)之外的零件,就认为这条生产线在这一天的生产过程可能出现了异常情况,需对当天的生产过程进行检查.
①从这一天抽检的结果看,是否需对当天的生产过程进行检查?
②在(x-3s,x+3s)之外的数据称为离群值,试剔除离群值,估计这条生产线当天生产的零件尺寸的均值与标准差.(精确到0.01)
附:样本(xi,yi)(i=1,2,…,n)的相关系数为
r=,
≈0.09.
20.
(本小题满分12分)设A,B为曲线C:y=上两点,A与B的横坐标之和为4.
(1)
求直线AB的斜率;
(2)
设M为曲线C上一点,C在M处的切线与直线AB平行,且AM⊥BM,求直线AB的方程.
21.
(本小题满分12分)已知函数f(x)=ex(ex-a)-a2x.
(1)
讨论f(x)的单调性;
(2)
若f(x)≥0,求a的取值范围.
请考生在第22,23题中任选一题作答,如果多做,则按所做的第一题计分.
22.
(本小题满分10分)选修44:坐标系与参数方程
在直角坐标系xOy中,曲线C的参数方程为(θ为参数),直线l的参数方程为(t为参数).
(1)
若a=-1,求C与l的交点坐标;
(2)
若C上的点到l距离的最大值为,求a的值.
23.
(本小题满分10分)选修45:不等式选讲
已知函数f(x)=-x2+ax+4,g(x)=|x+1|+|x-1|.
(1)
当a=1时,求不等式f(x)≥g(x)的解集;
(2)
若不等式f(x)≥g(x)的解集包含[-1,1],求a的取值范围.
2017年普通高等学校招生全国统一考试
数学文科(新课标Ⅰ卷)
1.
A 【解析】由题意得B=,从而A∩B=,A∪B={x|x<2}.故选A.
2.
B 【解析】在样本的几个特征量中,平均数反映集中趋势,标准差反映起伏大小,中位数不会因个别数据的异常发生改变,极差是最大值和最小值的差,一般用来制作频率分布直方图.故选B.
3.
C 【解析】因为i(1+i)2=2i2=-2,i2(1-i)=-1+i,(1+i)2=2i,i(1+i)=-1+i,由纯虚数的定义知选C.故选C.
4.
B 【解析】设正方形的边长为2,由该图形的中心对称性知图中黑色部分的面积为,又正方形的面积为4,所以P==.故选B.
5.
D 【解析】依题意,点F的坐标为(2,0),点P的坐标为(2,3),所以△PAF的面积为S=AP·PF=×1×3=.故选D.
6.
A 【解析】如图(1),O为BC的中点,连接OQ,易知AB∥OQ,OQ与平面MNQ显然不平行,故AB与平面MNQ不平行;B中,AB∥MQ,从而AB∥平面MNQ;C中,如图(2),C为AD的中点,易得AB∥CN,CN∥MQ,显然AB?平面MNQ,故AB∥平面MNQ;D中,显然NQ∥AB,又AB?平面MNQ,故AB∥平面MNQ.故选A.
图(1)
图(2)
(第6题)
7.
D 【解析】作出可行域如图中阴影部分所示,平移直线y=-x+z,可知z=x+y在点A(3,0)处取得最大值,即zmax=3.故选D.
(第7题)
C 【解析】设f(x)=,由f(x)+f(-x)=0知f(x)为奇函数,故排除B.由f(1)>0,可排除A;由f(π)=0,可排除D.故选C.
9.
C 【解析】由题易知,f(x)的定义域为(0,2),且f(x)=ln(-x2+2x),由复合函数单调性易判断f(x)在(0,1)上单调递增,在(1,2)上单调递减,所以选项A,B错误;又因为f(2-x)=ln(2-x)+ln[2-(2-x)]=ln(2-x)+lnx=f(x),所以f(x)的图象关于直线x=1对称,所以D选项错误,C正确.故选C.
10.
D 【解析】由n为偶数可知,执行框中应为n=n+2,又因为3n-2n>1
000时结束循环,因此,判断框中应为A≤1
000.故选D.
11.
B 【解析】因为sinB+sinA(sinC-cosC)=sin(A+C)+sinAsinC-sinAcosC=sinAcosC+cosAsinC+sinAsinC-sinAcosC=sinC(cosA+sinA)=0,因为sinC≠0,所以cosA+sinA=0,可解得A=,由正弦定理可得sinC==.又C∈,所以C=.故选B.
12.
A 【解析】若m<3,如图(1),易知点M在y轴上时,∠AMB取得最大值120°,此时∠MBO=30°,tan∠MBO===,解得m=1,故短轴长只能小于此边界情况才能满足题意,所以m∈(0,1].若m>3,如图(2),当M在x轴上时,∠AMB取最大值120°,同理可得tan30°===,所以m=9,当m≥9时,才能满足题意.综上,m∈(0,1]∪[9,+∞).故选A.
图(1)
图(2)
(第12题)
13.
7 【解析】由题意得,(a+b)·a=0,即a2+a·b=0,即5-m+2=0,解得m=7.
14.
y=x+1 【解析】由题意知y′=2x-,当x=1时,y′=1,y=2,从而切线的方程是y=x+1.
15.
【解析】由α∈,tanα=2,得sinα=,cosα=,从而cos=cosαcos+sinαsin=×+×=.
16.
36π 【解析】如图,O为球心,连接AO,BO,设SA=a,半径为R.因为SB=BC,所以BO⊥SC,又因为平面SCA⊥平面SCB,所以BO⊥平面SAC.因为SA=AC,SC是直径,所以BO=AO=a=SO,从而VS
ABC=·BO·S△ASC=×a×=9,解得a=3,从而R=a=3,球O的表面积为4πR2=36π.
(第16题)
17.
(1)
设{an}的公比为q,由题设可得解得q=-2,a1=-2.
故{an}的通项公式为an=(-2)n.
(2)
由(1)可得Sn==-+.
由于Sn+2+Sn+1=-+=2=2Sn,
故Sn+1,Sn,Sn+2成等差数列.
(1)
由已知∠BAP=∠CDP=90°,得AB⊥AP,CD⊥PD.
因为AB∥CD,所以AB⊥PD,
又AP∩PD=P,从而AB⊥平面PAD.
因为AB平面PAB,所以平面PAB⊥平面PAD.
(第18题)
(2)
如图,过点P作PE⊥AD,垂足为E.由(1)知,AB⊥平面PAD,故AB⊥PE,可得PE⊥平面ABCD.设AB=x,则由已知可得AD=x,PE=x.
故四棱锥P-ABCD的体积VP
-
ABCD=AB·AD·PE=x3.
由题设得x3=,故x=2,
从而PA=PD=2,AD=BC=2,PB=PC=2,
可得四棱锥P-ABCD的侧面积为
PA·PD+PA·AB+PD·DC+BC2sin60°=6+2.
19.
(1)
由样本数据得(x,i)(i=1,2,…,16)的相关系数为
r==≈-0.18.
由于|r|<0.25,因此可以认为这一天生产的零件尺寸不随生产过程的进行而系统地变大或变小.
(2)
①由于x=9.97,s≈0.212,由样本数据可以看出抽取的第13个零件的尺寸在(x-3s,x+3s)以外,因此需对当天的生产过程进行检查.
②剔除离群值,即第13个数据,剩下数据的平均数为
σ2=(16×9.97-9.22)=10.02,
这条生产线当天生产的零件尺寸的均值的估计值为10.02.
=16×0.2122+16×9.972≈1
591.134,
剔除第13个数据,剩下数据的样本方差为
(1
591.134-9.222-15×10.022)≈0.008,
故这条生产线当天生产的零件尺寸的标准差的估计值为≈0.09.
20.
(1)
设A(x1,y1),B(x2,y2),
则x1≠x2,y1=,y2=,x1+x2=4,
于是直线AB的斜率k===1.
(2)
由y=,得y′=,
设M(x3,y3),由题设知=1,解得x3=2,于是M(2,1).
设直线AB的方程为y=x+m,
故线段AB的中点为N(2,2+m),MN=|m+1|.
将y=x+m代入y=得x2-4x-4m=0.
当Δ=16(m+1)>0,即m>-1时,x1,2=2±2,
从而AB=|x1-x2|=4.
由题设知AB=2MN,即4=2(m+1),解得m=7,
所以直线AB的方程为y=x+7.
21.
(1)
函数f(x)的定义域为(-∞,+∞),f′(x)=2e2x-aex-a2=(2ex+a)(ex-a).
①若a=0,则f(x)=e2x,在(-∞,+∞)上单调递增.
②若a>0,则由f′(x)=0得x=lna.
当x∈(-∞,lna)时,f′(x)<0;当x∈(lna,+∞)时,f′(x)>0.
故f(x)在(-∞,lna)上单调递减,在(lna,+∞)上单调递增.
③若a<0,则由f′(x)=0得x=ln.
当x∈时,f′(x)<0;当x∈(ln,+∞)时,f′(x)>0.故f(x)在上单调递减,在上单调递增.
(2)
①若a=0,则f(x)=e2x,所以f(x)≥0.
②若a>0,则由(1)得,当x=lna时,f(x)取得最小值,最小值为f(lna)=-a2lna,当且仅当-a2lna≥0,即0③若a<0,则由(1)得,当x=ln时,f(x)取得最小值,最小值为f=a2,从而当且仅当a2≥0,即-2e≤a<0时,f(x)≥0.
综上,a的取值范围是[-2e,1].
22.
(1)
曲线C的普通方程为+y2=1.
当a=-1时,直线l的普通方程为x+4y-3=0.
由解得或
从而C与l的交点坐标为(3,0),.
直线l的普通方程为x+4y-a-4=0,
故C上的点(3cosθ,sinθ)到l的距离为d=.
当a≥-4时,d的最大值为
.由题设得=,所以a=8.
当a<-4时,d的最大值为.由题设得=,所以a=-16.
综上,a=8或a=-16.
23.
(1)
当a=1时,不等式f(x)≥g(x)等价于
x2-x+|x+1|+|x-1|-4≤0. ①
当x<-1时,①式化为x2-3x-4≤0,无解;
当-1≤x≤1时,①式化为x2-x-2≤0,从而-1≤x≤1;
当x>1时,①式化为x2+x-4≤0,从而1所以f(x)≥g(x)的解集为.
(2)
当x∈[-1,1]时,g(x)=2.
所以f(x)≥g(x)的解集包含[-1,1],等价于当x∈[-1,1]时f(x)≥2.
又f(x)在[-1,1]上的最小值必为f(-1)与f(1)之一,
所以f(-1)≥2且f(1)≥2,得-1≤a≤1.
所以a的取值范围为[-1,1].
2018年普通高等学校招生全国统一考试
数学文科(新课标Ⅰ卷)
一、
选择题:本大题共12小题,每小题5分.
1.
已知集合A={0,2},B={-2,-1,0,1,2},则A∩B等于( )
A.
{0,2}
B.
{1,2}
C.
{0}
D.
{-2,-1,0,1,2}
2.
设z=+2i,则|z|等于( )
A.
0
B.
C.
1
D.
3.
某地区经过一年的新农村建设,农村的经济收入增加了一倍,实现翻番.为更好地了解该地区农村的经济收入变化情况,统计了该地区新农村建设前后农村的经济收入构成比例,得到如下饼图:
(第3题)
则下面结论中不正确的是( )
A.
新农村建设后,种植收入减少
B.
新农村建设后,其他收入增加了一倍以上
C.
新农村建设后,养殖收入增加了一倍
D.
新农村建设后,养殖收入与第三产业收入的总和超过了经济收入的一半
4.
已知椭圆C:+=1的一个焦点为(2,0),则C的离心率为( )
A.
B.
C.
D.
5.
已知圆柱的上、下底面的中心分别为O1,O2,过直线O1O2的平面截该圆柱所得的截面是面积为8的正方形,则该圆柱的表面积为( )
A.
12π
B.
12π
C.
8π
D.
10π
6.
设函数f(x)=x3+(a-1)x2+ax,若f(x)为奇函数,则曲线y=f(x)在点(0,0)处的切线方程为( )
A.
y=-2x
B.
y=-x
C.
y=2x
D.
y=x
7.
在△ABC中,AD为BC边上的中线,E为AD的中点,则等于( )
A.
-
B.
-
C.
+
D.
+
8.
已知函数f(x)=2cos2x-sin2x+2,则( )
A.
f(x)的最小正周期为π,最大值为3
B.
f(x)的最小正周期为π,最大值为4
C.
f(x)的最小正周期为2π,最大值为3
D.
f(x)的最小正周期为2π,最大值为4
9.
某圆柱的高为2,底面周长为16,其三视图如图所示.圆柱表面上的点M在正视图上的对应点为A,圆柱表面上的点N在侧视图上的对应点为B,则在此圆柱侧面上,从M到N的路径中,最短路径的长度为( )
A.
2
B.
2
C.
3
D.
2
(第9题)
10.
在长方体ABCD-A1B1C1D1中,AB=BC=2,AC1与平面BB1C1C所成的角为30°,则该长方体的体积为( )
A.
8
B.
6
C.
8
D.
8
11.
已知角α的顶点为坐标原点,始边与x轴的非负半轴重合,终边上有两点A(1,a),B(2,b),且cos2α=,则|a-b|等于( )
A.
B.
C.
D.
1
12.
设函数f(x)=则满足f(x+1)A.
(-∞,-1]
B.
(0,+∞)
C.
(-1,0)
D.
(-∞,0)
填空题:本大题共4小题,每小题5分.
13.
已知函数f(x)=log2(x2+a),若f(3)=1,则a=________.
14.
若x,y满足约束条件则z=3x+2y的最大值为________.
15.
若直线y=x+1与圆x2+y2+2y-3=0交于A,B两点,则AB=________.
16.
已知△ABC的内角A,B,C的对边分别为a,b,c,bsinC+csinB=4asinBsinC,b2+c2-a2=8,则△ABC的面积为________.
三、
解答题:解答时应写出必要的文字说明、证明过程或演算步骤.
17.
(本小题满分12分)已知数列{an}满足a1=1,nan+1=2(n+1)an,设bn=.
(1)
求b1,b2,b3的值;
(2)
判断数列{bn}是否为等比数列,并说明理由;
(3)
求{an}的通项公式.
18.
(本小题满分12分)如图,在平行四边形ABCM中,AB=AC=3,∠ACM=90°,以AC为折痕将△ACM折起,使点M到达点D的位置,且AB⊥DA.
(1)
求证:平面ACD⊥平面ABC;
(2)
若Q为线段AD上一点,P为线段BC上一点,且BP=DQ=DA,求三棱锥Q-ABP的体积.
(第18题)
19.
(本小题满分12分)某家庭记录了未使用节水龙头50天的日用水量数据(单位:m3)和使用了节水龙头50天的日用水量数据,得到频数分布表如下:
未使用节水龙头50天的日用水量频数分布表
日用
水量
[0,0.1)
[0.1,0.2)
[0.2,0.3)
[0.3,0.4)
[0.4,0.5)
[0.5,0.6)
[0.6,0.7)
频数
1
3
2
4
9
26
5
使用了节水龙头50天的日用水量频数分布表
日用水量
[0,0.1)
[0.1,0.2)
[0.2,0.3)
[0.3,0.4)
[0.4,0.5)
[0.5,0.6)
频数
1
5
13
10
16
5
(1)
作出使用了节水龙头50天的日用水量数据的频率分布直方图;
(2)
估计该家庭使用节水龙头后,日用水量小于0.35
m3的概率;
(3)
估计该家庭使用节水龙头后,一年能节省多少水?(一年按365天计算,同一组中的数据以这组数据所在区间中点的值作代表).
(第19题)
20.
(本小题满分12分)设抛物线C:y2=2x,点A(2,0),B(-2,0),过点A的直线l与C交于M,N两点.
(1)
当l与x轴垂直时,求直线BM的方程;
(2)
求证:∠ABM=∠ABN.
21.
(本小题满分12分)已知函数f(x)=aex-lnx-1.
(1)
设x=2是f(x)的极值点,求a的值和f(x)的单调区间;
(2)
求证:当a≥时,f(x)≥0.
请考生在第22,23题中任选一题作答,如果多做,则按所做的第一题计分.
22.
(本小题满分10分)选修44:坐标系与参数方程
在直角坐标系xOy中,曲线C1的方程为y=k|x|+2.以坐标原点为极点,x轴正半轴为极轴建立极坐标系,曲线C2的极坐标方程为ρ2+2ρcosθ-3=0.
(1)
求C2的直角坐标方程;
(2)
若C1与C2有且仅有三个公共点,求C1的方程.
23.
(本小题满分10分)选修45:不等式选讲
已知f(x)=|x+1|-|ax-1|.
(1)
当a=1时,求不等式f(x)>1的解集;
(2)
若x∈(0,1)时不等式f(x)>x成立,求a的取值范围.
2018年普通高等学校招生全国统一考试
数学文科(新课标Ⅰ卷)
1.
A 【解析】A∩B={0,2}.故选A.
2.
C 【解析】因为z=+2i=+2i=-i+2i=i,所以|z|=1.故选C.
3.
A 【解析】假设新农村建设前农村的经济收入为a,新农村建设后,农村的经济收入增加了一倍,实现翻番为2a,所以种植收入为37%×2a=74%a>60%a,故A错.故选A.
4.
C 【解析】在椭圆中,a===2,所以离心率e==.故选C.
5.
B 【解析】设圆柱底面半径为r,则(2r)·(2r)=4r2=8,解得r=,所以该圆柱的表面积为S=(2πr)·(2r)+2πr2=12π.故选B.
6.
D 【解析】因为f(x)为奇函数,所以a-1=0,即a=1,所以f(x)=x3+x,则f′(x)=3x2+1,则曲线y=f(x)在点(0,0)处的切线方程为y-0=f′(0)(x-0),即y=x.故选D.
7.
A 【解析】=+=-=·(+)-(-)=-.故选A.
8.
B 【解析】f(x)=1+cos2x-+2=cos2x+,故最小正周期为π,最大值为+=4.故选B.
9.
B 【解析】根据题意,圆柱的侧面展开图是长为16,宽为2的长方形MDEF,如图,由其三视图可知,点A对应长方形MDEF中的点M,点B为DE上靠近D点的四等分点.则AB的最短路径为线段AB==2.故选B.
(第9题)
10.
C 【解析】如图,设CC1=c,由题易知∠AC1B=30°,则tan∠AC1B===,解得c=2,所以体积V=2×2×2=8.故选C.
(第10题)
B 【解析】由题意知tanα=a=,而cos2α====,所以a2=,所以|a-b|=|a|=.故选B.
12.
D 【解析】画出f(x)的图象,观察图象分析可知存在两种情况:①2x(第12题)
13.
-7 【解析】因为f(3)=log2(32+a)=1,解得a+9=2,所以a=-7.
14.
6 【解析】作出可行域如图中阴影部分所示,由图可知目标函数z在点(2,0)处取得最大值,为6.
(第14题)
15.
2 【解析】圆x2+y2+2y-3=0化为标准方程为x2+(y+1)2=4,所以圆心为(0,-1),半径为2,圆心到直线y=x+1的距离d==,所以AB=2=2=2.
16.
【解析】由正弦定理得2sinBsinC=4sinAsinBsinC,因为sinB·sinC≠0,所以sinA=.又因为2bccosA=b2+c2-a2=8,所以A为锐角,所以cosA=,所以bc=,所以△ABC的面积S=bcsinA=.
17.
(1)
由条件可得an+1=an.
将n=1代入,得a2=4a1,而a1=1,所以a2=4.
将n=2代入,得a3=3a2,所以a3=12.
从而b1=1,b2=2,b3=4.
(2)
{bn}是首项为1,公比为2的等比数列.
由条件可得=,即bn+1=2bn,又b1=1,
所以{bn}是首项为1,公比为2的等比数列.
(3)
由(2)可得=2n-1,所以an=n·2n-1.
18.
(1)
由已知可得∠BAC=90°,所以AB⊥AC.
又AB⊥AD,AD∩AC=A,所以AB⊥平面ACD.
因为AB平面ABC,所以平面ACD⊥平面ABC.
(第18题)
(2)
由已知可得,DC=CM=AB=AC=3,所以DA=3.
又BP=DQ=DA,所以BP=2.
如图,过点Q作QE⊥AC,垂足为E,则QE∥DC且QE=DC.
由已知及(1)可得DC⊥平面ABC,所以QE⊥平面ABC,QE=1.
因此,三棱锥Q-ABP的体积为VQ
-
ABP=×QE×S△ABP=×1××3×2sin45°=1.
19.
(1)
如图所示.
(第19题)
(2)
由题可知,日用水量在[0.3,0.4)之间的天数为10天,所以可估计在[0.3,0.35)的天数为5天,所以估计日用水量小于0.35
m3的概率为=0.48.
(3)
由题可知,50天的节约水量为(0.05×1+0.15×3+0.25×2+0.35×4+0.45×9+0.55×26+0.65×5)-(0.05×1+0.15×5+0.25×13+0.35×10+0.45×16+0.55×5)=6.5,一年的节约用水量为×6.5=47.45,所以一年能节约47.45
m3水.
20.
(1)
当l与x轴垂直时,l的方程为x=2,可得点M的坐标为(2,2)或(2,-2),所以直线BM的方程为y=x+1或y=-x-1.
(2)
当l与x轴垂直时,AB为MN的垂直平分线,
所以∠ABM=∠ABN.
当l与x轴不垂直时,设l的方程为y=k(x-2)(k≠0),M(x1,y1),N(x2,y2),
则x1>0,x2>0.
由得ky2-2y-4k=0,则y1+y2=,y1y2=-4.
直线BM,BN的斜率之和为
kBM+kBN=+=,①
将x1=+2,x2=+2及y1+y2=,y1y2=-4代入①式分子,
可得x2y1+x1y2+2(y1+y2)===0,
所以kBM+kBN=0,可知BM,BN的倾斜角互补,
所以∠ABM=∠ABN.
综上,∠ABM=∠ABN.
21.
(1)
f(x)的定义域为(0,+∞),f′(x)=aex-.
由题设知,f′(2)=0,所以a=,
从而f(x)=ex-lnx-1,f′(x)=ex-.
当02时,f′(x)>0,
所以f(x)的单调减区间为(0,2),单调增区间为(2,+∞).
(2)
当a≥时,f(x)≥-lnx-1.
设g(x)=-lnx-1,则g′(x)=-.
当01时,g′(x)>0,
所以x=1是g(x)的最小值点.
故当x>0时,g(x)≥g(1)=0.
因此,当a≥时,f(x)≥0.
22.
(1)
由x=ρcosθ,x2+y2=ρ2,得C2的直角坐标方程为x2+y2+2x-3=0,即(x+1)2+y2=4.
(2)
由(1)知C2是圆心为A(-1,0),半径为2的圆.
由题设知,C1是过点B(0,2)且关于y轴对称的两条射线.记y轴右边的射线为l1,y轴左边的射线为l2.由于B在圆C2的外面,故C1与C2有且仅有三个公共点等价于l1与C2只有一个公共点且l2与C2有两个公共点,或l2与C2只有一个公共点且l1与C2有两个公共点.
当l1与C2只有一个公共点时,点A到l1所在直线的距离为2,所以=2,故k=-或k=0.经检验,当k=0时,l1与C2没有公共点;当k=-时,l1与C2只有一个公共点,l2与C2有两个公共点.
当l2与C2只有一个公共点时,点A到l2所在直线的距离为2,
所以=2,故k=0或k=.
经检验,当k=0时,l1与C2没有公共点;当k=时,l2与C2没有公共点.
综上,所求C1的方程为y=-|x|+2.
23.
(1)
当a=1时,f(x)=|x+1|-|x-1|,
即f(x)=解得x>.
故不等式f(x)>1的解为.
(2)
当x∈(0,1)时|x+1|-|ax-1|>x成立等价于当x∈(0,1)时|ax-1|<1成立.
若a≤0,则当x∈(0,1)时|ax-1|≥1;
若a>0,|ax-1|<1的解为0
数学文科(新课标Ⅰ卷)一、
选择题:本大题共12小题,每小题5分,
在每小题给出的四个选项中,只有一项是符合题目要求的.
1.
已知集合M={x|-1
A.
(-2,1)
B.
(-1,1)
C.
(1,3)
D.
(-2,3)
2.
若tan
α>0,则( )
A.
sin
α>0
B.
cos
α>0
C.
sin
2α>0
D.
cos
2α>0
3.
设复数z=+i(i为虚数单位),则|z|等于( )
A.
B.
C.
D.
2
4.
已知双曲线-=1(a>0)的离心率为2,则
a等于( )
A.
2
B.
C.
D.
1
5.
设函数f(x),g(x)的定义域都为R,且f(x)是奇函数,g(x)是偶函数,则下列结论中正确的是( )
A.
f(x)g(x)是偶函数
B.
|f(x)|g(x)是奇函数
C.
f(x)|g(x)|是奇函数
D.
|f(x)g(x)|是奇函数
6.
设D,E,F分别为△ABC的三边BC,CA,AB的中点,则+等于( )
A.
B.
C.
D.
7.
在函数①y=cos|2x|,②y=|cos
x|,③y=cos
,④y=tan中,最小正周期为π的所有函数为( )
A.
①②③
B.
①③④
C.
②④
D.
①③
8.
如图,网格纸的各小格都是正方形,粗实线画出的是一个几何体的三视图,则这个几何体是( )
A.
三棱锥
B.
三棱柱
C.
四棱锥
D.
四棱柱
(第8题)
9.
执行如图所示的程序框图,若输入的a,b,k分别为1,2,3,则输出的M等于( )
A.
B.
C.
D.
(第9题)
10.
已知抛物线C:y2=x的焦点为F,A(x0,y0)是C上一点,AF=x0,则x0等于( )
A.
1
B.
2
C.
4
D.
8
11.
设x,y满足约束条件且z=x+ay的最小值为7,则实数a等于( )
A.
-5
B.
3
C.
-5或3
D.
5或-3
12.
已知函数f(x)=ax3-3x2+1,若f(x)存在唯一的零点x0,且x0>0,则实数a的取值范围是( )
A.
(2,+∞)
B.
(1,+∞)
C.
(-∞,-2)
D.
(-∞,-1)
二、
填空题:本大题共4小题,每小题5分.
13.
将2本不同的数学书和1本语文书在书架上随机排成一行,则2本数学书相邻的概率为________.
14.
甲、乙、丙三位同学被问到是否去过A,B,C三个城市时,
甲说:我去过的城市比乙多,但没去过B城市;
乙说:我没去过C城市;
丙说:我们三人去过同一城市.
由此可判断乙去过的城市为________.
15.
设函数f(x)=则使得f(x)≤2成立的x的取值范围是________.
16.
如图,为测量山高MN,选择A和另一座山的山顶C为测量观测点.从点A测得点M的仰角∠MAN=60°,点C的仰角∠CAB=45°以及∠MAC=75°,从点C测得∠MCA=60°.已知山高BC=100m,则山高MN=________m.
(第16题)
三、
解答题:解答应写出文字说明、证明过程或演算步骤.
17.
(本小题满分12分)已知{an}是递增的等差数列,a2,a4是方程x2-5x+6=0的根.
(1)
求数列{an}的通项公式;
(2)
求数列的前n项和.
18.
(本小题满分12分)从某企业生产的某种产品中抽取100件,测量这些产品的一项质量指标值,由测量结果得如下频数分布表:
质量指
标值
分组
[75,85)
[85,95)
[95,105)
[105,115)
[115,125)
频数
6
26
38
22
8
(1)
在下表中作出这些数据的频率分布直方图;
(第18题)
(2)
估计这种产品质量指标值的平均数及方差(同一组中的数据用该组区间的中点值作代表);
(3)
根据以上抽样调查数据,能否认为该企业生产的这种产品符合“质量指标值不低于95的产品至少要占全部产品的80%”的规定?
19.
(本小题满分12分)如图,在三棱柱ABC-A1B1C1中,侧面BB1C1C为菱形,B1C的中点为O,且AO⊥平面BB1C1C.
(1)
求证:B1C⊥AB;
(2)
若AC⊥AB1,∠CBB1=60°,BC=1,求三棱柱ABC-A1B1C1的高.
(第19题)
20.
(本小题满分12分)已知点P(2,2),圆C:x2+y2-8y=0,过点P的动直线l与圆C交于A,B两点,线段AB的中点为M,O为坐标原点.
(1)
求M的轨迹方程;
(2)
当OP=OM时,求l的方程及△POM的面积.
21.
(本小题满分12分)设函数f(x)=aln
x+x2-bx(a≠1),曲线y=f(x)在点(1,f(1))处的切线斜率为0.
(1)
求b;
(2)
若存在x0≥1,使得f(x0)<,求实数a的取值范围.
请考生在第22,23,24题中任选一题作答,如果多做,则按所做的第一题计分.
22.
(本小题满分10分)选修41:几何证明选讲
如图,四边形ABCD是圆O的内接四边形,AB的延长线与DC的延长线交于点E,且CB=CE.
(1)
求证:∠D=∠E;
(2)
设AD不是圆O的直径,AD的中点为M,且MB=MC,求证:△ADE为等边三角形.
(第22题)
23.
(本小题满分10分)选修44:坐标系与参数方程
已知曲线C:+=1,直线l:(t为参数).
(1)
写出曲线C的参数方程与直线l的普通方程;
(2)
过曲线C上任意一点P作与l夹角为30°的直线,交l于点A,求PA的最大值与最小值.
24.
(本小题满分10分)选修45:不等式选讲
若a>0,b>0,且+=.
(1)
求a3+b3的最小值;
(2)
是否存在a,b,使得2a+3b=6?并说明理由.
2014年普通高等学校招生全国统一考试 数学文科(新课标Ⅰ卷)
1.
B 【解析】借助数轴可得M∩N=(-1,1),故选B.
2.
C 【解析】由tan
α>0,可得α的终边在第一象限或第三象限,此时sin
α与cos
α同号,故sin
2α=2sin
αcos
α>0,故选C.
3.
B 【解析】+i=+i=+i=+i,则|z|==,故选B.
4.
D 【解析】因为双曲线的方程为-=1,所以e2==4,因此a2=1,a=1,故选D.
5.
C 【解析】因为f(x)为奇函数,g(x)为偶函数,故f(x)g(x)为奇函数,|f(x)|g(x)为偶函数,f(x)|g(x)|为奇函数,|f(x)g(x)|为偶函数,故选C.
6.
A 【解析】+=(+)+(+)=(+)=,故选A.
7.
A 【解析】①y=cos|2x|的最小正周期为π;②y=|cos
x|的最小正周期为π;③y=cos的最小正周期为π;④y=tan(2x-)的最小正周期为,故选A.
8.
B 【解析】由题意知,该几何体的三视图为一个三角形和两个四边形,经分析可知该几何体为三棱柱,故选B.
9.
D 【解析】第一次循环:M=,a=2,b=,n=2;第二次循环:M=,a=,b=,n=3;第三次循环:M=,a=,b=,n=4,则输出M=,故选D.
10.
A 【解析】由题意知抛物线的准线方程为x=-.因为AF=x0,根据抛物线的定义可得x0+=AF=x0,解得x0=1,故选A.
11.
B 【解析】当a≥1时,联立方程组解得代入x+ay=7中,解得a=3或a=-5(舍去).当a<1时,不符合条件,故选B.
12.
C 【解析】由题意知f′(x)=3ax2-6x=3x(ax-2),当a=0时,不满足题意.当a≠0时,令f′(x)=0,解得x=0或x=.当a>0时,f(x)在(-∞,0),上单调递增,在上单调递减.又f(0)=1,此时f(x)在(-∞,0)上存在零点,不满足题意;当a<0时,f(x)在,(0,+∞)上单调递减,在上单调递增,要使f(x)存在唯一的零点x0,且x0>0,则需f>0,即a×-3×+1>0,解得a<-2,故选C.
13.
【解析】设2本数学书分别为A,B,语文书为C,则所有的排放顺序有ABC,ACB,BAC,BCA,CAB,CBA,共6种情况,其中数学书相邻的有ABC,BAC,CAB,CBA,共4种情况,故2本数学书相邻的概率P==.
14.
A 【解析】根据甲和丙的回答推测乙没去过B城市,又知乙没去过C城市,故乙去过A城市.
15.
(-∞,8] 【解析】当x<1时,由ex-1≤2,得x≤1+ln
2,所以x<1;当x≥1时,由x≤2,得x≤8,所以1≤x≤8.综上,符合题意的x的取值范围是{x|x≤8}.
16.
150 【解析】在△ABC中,AC=100m,在△MAC中,=,解得MA=100m,在△MNA中,MN=MAsin
60°=150(m).
17.
(1)
方程x2-5x+6=0的两根为2,3,由题意得a2=2,a4=3.设数列{an}的公差为d,则a4-a2=2d,故d=,从而a1=,
所以数列{an}的通项公式为an=n+1.
(2)
设的前n项和为Sn,由(1)知=,则
Sn=++…++,
Sn=++…++.
两式相减得
Sn=+-
=+-.
所以Sn=2-.
18.
(1)
(第18题)
(2)
质量指标值的样本平均数为
=80×0.06+90×0.26+100×0.38+110×0.22+120×0.08=100.
质量指标值的样本方差为
s2=(-20)2×0.06+(-10)2×0.26+0×0.38+102×0.22+202×0.08=104.
所以这种产品质量指标值的平均数的估计值为100,方差的估计值为104.
(3)
质量指标值不低于95的产品所占比例的估计值为
0.38+0.22+0.08=0.68.
由于该估计值小于0.8,故不能认为该企业生产的这种产品符合“质量指标值不低于95的产品至少要占全部产品80%”的规定.
19.
(1)
如图,连接BC1,则O为B1C与BC1的交点.
因为侧面BB1C1C为菱形,所以B1C⊥BC1.
又AO⊥平面BB1C1C,所以B1C⊥AO,故B1C⊥平面ABO.
由于AB平面ABO,故B1C⊥AB.
(2)
如图,作OD⊥BC,垂足为D,连接AD.作OH⊥AD,垂足为H.由于BC⊥AO,BC⊥OD,故BC⊥平面AOD,所以OH⊥BC.
(第19题)
又OH⊥AD,所以OH⊥平面ABC.
因为∠CBB1=60°,所以△CBB1为等边三角形.
又BC=1,可得OD=.
由于AC⊥AB1,所以OA=B1C=.
由OH·AD=OD·OA,且AD==,
得OH=.
又O为B1C的中点,所以点B1到平面ABC的距离为,
故三棱柱ABC-A1B1C1的高为.
20.
(1)
圆C的方程可化为x2+(y-4)2=16,所以圆心为C(0,4),半径为4.
设M(x,y),则=(x,y-4),=(2-x,2-y).由题设知·=0,故x(2-x)+(y-4)(2-y)=0,即(x-1)2+(y-3)2=2.
由于点P在圆C的内部,所以M的轨迹方程是(x-1)2+(y-3)2=2.
(2)
由(1)可知M的轨迹是以点N(1,3)为圆心、为半径的圆.
由于OP=OM,故O在线段PM的垂直平分线上.
又P在圆N上,从而ON⊥PM.
因为ON的斜率为3,所以直线l的斜率为-,
故直线l的方程为y=-x+.
又OM=OP=2,O到l的距离为,PM=,
所以△POM的面积为.
21.
(1)
f′(x)=+(1-a)x-b.
由题设知f′(1)=0,解得b=1.
(2)
f(x)的定义域为(0,+∞),由(1)知,f(x)=aln
x+x2-x,
f′(x)=+(1-a)x-1=(x-1).
①若a≤,则≤1,故当x∈(1,+∞)时,f′(x)>0,f(x)在(1,+∞)上单调递增.
所以存在x0≥1,使得f(x0)<的充要条件为f(1)<,即-1<,解得--1
③若a>1,则f(1)=-1=<恒成立.
综上,实数a的取值范围是(--1,-1)∪(1,+∞).
22.
(1)
由题设知A,B,C,D四点共圆,
所以∠D=∠CBE.
因为CB=CE,
所以∠CBE=∠E,故∠D=∠E.
(2)
如图,取BC的中点N,连接MN,由MB=MC,
知MN⊥BC,故O在直线MN上.
(第22题)
又AD不是圆O的直径,M为AD的中点,
故OM⊥AD,即MN⊥AD,
所以AD∥BC,故∠A=∠CBE.
又∠CBE=∠E,故∠A=∠E.
由(1)知∠D=∠E,所以△ADE为等边三角形.
23.
(1)
曲线C的参数方程为(θ为参数).
直线l的普通方程为2x+y-6=0.
(2)
曲线C上任意一点P(2cos
θ,3sin
θ)到直线l的距离为
d=|4cos
θ+3sin
θ-6|.
则PA==|5sin(θ+α)-6|,其中α为锐角,且tan
α=.
当sin(θ+α)=-1时,PA取得最大值,最大值为.
当sin(θ+α)=1时,PA取得最小值,最小值为.
24.
(1)
由=+≥,得ab≥2,当且仅当a=b=时等号成立.
故a3+b3≥2≥4,当且仅当a=b=时等号成立.
所以a3+b3的最小值为4.
(2)
由(1)知2a+3b≥2·≥4.
由于4>6,从而不存在a,b,使得2a+3b=6.
2015年普通高等学校招生全国统一考试
数学文科(新课标Ⅰ卷)
一、
选择题:本大题共12小题,每小题5分,
在每小题给出的四个选项中,只有一项是符合题目要求的.
1.
已知集合A={x|x=3n+2,n∈N},B={6,8,10,12,14},则集合A∩B中的元素个数为( )
A.
5
B.
4
C.
3
D.
2
2.
已知点A(0,1),B(3,2),向量=(-4,-3),则向量等于( )
A.
(-7,-4)
B.
(7,4)
C.
(-1,4)
D.
(1,4)
3.
已知复数z满足(z-1)i=1+i,则z等于( )
A.
-2-i
B.
-2+i
C.
2-i
D.
2+i
4.
如果3个正整数可作为一个直角三角形三条边的边长,则称这3个数为一组勾股数,从1,2,3,4,5中任取3个不同的数,则这3个数构成一组勾股数的概率为( )
A.
B.
C.
D.
已知椭圆E的中心在坐标原点,离心率为,E的右焦点与抛物线C:y2=8x的焦点重合,A,B是C的准线与E的两个交点,则AB等于( )
3
B.
6
C.
9
D.
12
6.
《九章算术》是我国古代内容极为丰富的数学名著,书中有如下问题:“今有委米依垣内角,下周八尺,高五尺,问:积及为米几何?”其意思为:“在屋内墙角处堆放米(如图,米堆为一个圆锥的四分之一),米堆底部的弧长为8尺,米堆的高为5尺,问米堆的体积和堆放的米各为多少?”已知1斛米的体积约为1.62立方尺,圆周率约为3,估算出堆放的米约有( )
A.
14斛
B.
22斛
C.
36斛
D.
66斛
(第6题)
7.
已知{an}是公差为1的等差数列,Sn为{an}的前n项和,若S8=4S4,则a10的值为( )
A.
B.
C.
10
D.
12
8.
已知函数f(x)=cos(ωx+φ)的部分图象如图所示,则f(x)的单调减区间为( )
A.
,k∈Z
B.
,k∈Z
C.
,k∈Z
D.
,k∈Z
(第8题)
9.
执行如图所示的程序框图,若输入的t=0.01,则输出的n等于( )
A.
5
B.
6
C.
7
D.
8
(第9题
10.
已知函数f(x)=且f(a)=-3,则f(6-a)等于( )
A.
-
B.
-
C.
-
D.
-
11.
圆柱被一个平面截去一部分后与半球(半径为r)组成一个几何体,该几何体的三视图中的正视图和俯视图如图所示,若该几何体的表面积为16+20π,则r等于( )
A.
1
B.
2
C.
4
D.
8
(第11题)
12.
设函数y=f(x)的图象与y=2x+a的图象关于直线y=-x对称,且f(-2)+f(-4)=1,则a等于( )
A.
-1
B.
1
C.
2
D.
4
二、
填空题:本大题共4小题,每小题5分.
13.
在数列{an}中,a1=2,an+1=2an,Sn为{an}的前n项和,若Sn=126,则n=________.
14.
已知函数f(x)=ax3+x+1的图象在点(1,f(1))处的切线过点(2,7),则实数a=________.
15.
若变量x,y满足约束条件则z=3x+y的最大值为________.
16.
已知F是双曲线C:x2-=1的右焦点,P是C左支上一点,A(0,6),当△APF周长最小时,该三角形的面积为________.
三、
解答题:解答应写出文字说明、证明过程或演算步骤.
17.
(本小题满分12分)已知a,b,c分别是△ABC内角A,B,C的对边,sin2B=
2sin
Asin
C.
(1)
若a=b,求cos
B的值;
(2)
若角B=90°,且a=,求△ABC的面积.
18.
(本小题满分12分)如图,四边形ABCD为菱形,G为AC与BD的交点,BE⊥平面ABCD.
(1)
求证:平面AEC⊥平面BED;
(2)
若∠ABC=120°,AE⊥EC,三棱锥E-ACD的体积为,求该三棱锥的侧面积.
(第18题)
19.
(本小题满分12分)某公司为确定下一年度投入某种产品的宣传费,需了解年宣传费x(单位:千元)对年销售量y(单位:t)和年利润z(单位:千元)的影响,对近8年的宣传费xi和年销售量yi(i=1,2,…,8)的数据作了初步处理,得到如图所示的散点图及一些统计量的值.
(第19题)
(1)
根据散点图判断y=a+bx与y=c+d
哪一个适宜作为年销售量y关于年宣传费x的回归方程类型;(给出判断即可,不必说明理由)
(2)
根据(1)的判断结果及表中数据,建立y关于x的回归方程;
(3)
已知这种产品的年利润z与x,y的关系为z=0.2y-x,根据(2)的结果回答下列问题:
①当年宣传费x=49时,年销售量及年利润的预报值是多少?
②当年宣传费x为何值时,年利润的预报值最大?
附:对于一组数据(u1,v1),(u2,v2),…,(un,vn),其回归直线v=α+βu的斜率和截距的最小二乘估计分别为
=,=v-u.
20.
(本小题满分12分)已知过点A(0,1)且斜率为k的直线l与圆C:(x-2)2+(y-3)2=1交于M,N两点.
(1)
求斜率k的取值范围;
(2)
若·=12,其中O为坐标原点,求MN.
21.
(本小题满分12分)设函数f(x)=e2x-aln
x.
(1)
讨论f(x)的导函数f′(x)的零点的个数;
(2)
求证:当a>0时,f(x)≥2a+aln
.
请考生在第22,23,24题中任选一题作答,如果多做,则按所做的第一题计分.
22.
(本小题满分10分)选修41:几何证明选讲
如图,AB是圆O的直径,AC是圆O的切线,BC交圆O于点E.
(1)
若D为AC中点,求证:DE是圆O的切线;
(2)
若OA=CE,求∠ACB的大小.
(第22题)
23.
(本小题满分10分)选修44:坐标系与参数方程
在平面直角坐标系xOy中,直线C1:x=-2,圆C2:(x-1)2+(y-2)2=1,以坐标原点为极点,x轴正半轴为极轴建立极坐标系.
(1)
求C1,C2的极坐标方程.
(2)
若直线C3的极坐标方程为θ=(ρ∈R),设C2,C3的交点为M,N,求△C2MN的面积.
24.
(本小题满分10分)选修45:不等式选讲
已知函数f(x)=|x+1|-2|x-a|,a>0.
(1)
当a=1时,求不等式f(x)>1的解集;
(2)
若f(x)的图象与x轴围成的三角形面积大于6,求实数a的取值范围.
2015年普通高等学校招生全国统一考试
数学文科(新课标Ⅰ卷)
1.
D 【解析】因为A={x|x=3n+2,n∈N}={…,2,5,8,11,14,…},所以A∩B={8,14},集合A∩B中的元素个数为2.
2.
A 【解析】设C(x,y),因为=(x,y-1)=(-4,-3),所以所以
C(-4,-2),所以=(-4-3,-2-2)=(-7,-4).
3.
C 【解析】设z=x+yi,因为(z-1)i=[(x-1)+yi]i=-y+(x-1)i=1+i,所以所以z=2-i.
4.
C 【解析】因为从1,2,3,4,5中任取3个不同的数共有10种情况,又构成一组勾股数的情况有1种(3,4,5),所以所求概率为.
5.
B 【解析】设椭圆E的标准方程为+=1,依题意得=,c=2,解得a=4,所以b2=12,所以椭圆E的标准方程为+=1,令x=-2,解得y=±3,所以AB=3-
(-3)=6.
6.
B 【解析】由题意可知米堆的下底面圆半径为r==,所以米堆的体积为V=×Sh=××3××5=,所以估算出堆放的米约有≈21.94≈22(斛).
7.
B 【解析】由S8=4S4,得=4×,化简得a8=a1+2a4,又d=1,可求得a1=,所以a10=a1+9d=+9=.
8.
D 【解析】由图可知,T=-=1,所以T=2=,从而ω=π.由f=cos=0及图象的单调性,可知φ=.令2kπ<πx+<π+2kπ,k∈Z,解得2k-
C 【解析】第一次循环:S=,m=,n=1;第二次循环:S=,m=,n=2;
第三次循环:S=,m=,n=3;第四次循环:S=,m=,n=4;
第五次循环:S=,m=,n=5;第六次循环:S=,m=,n=6;
第七次循环:S=,m=,n=7.此时S=<0.01,循环结束.
10.
A 【解析】当a≤1时,由2a-1-2=-3,知a无解;
当a>1时,由-log2(a+1)=-3,解得a=7,
所以f(6-a)=f(6-7)=f(-1)=2-1-1-2=-2=-.
11.
B 【解析】该几何体由一个半球和半个圆柱组成,圆柱的高为2r,底面半径和球的半径均为r,组合体的表面积为S=2×πr2+πr×2r+2r×2r+×4πr2=5πr2+4r2=16+20π,所以r2=4,r=2.
12.
C 【解析】依题意得-x=2-y+a,即f(x)=-log2(-x)+a.
因为f(-2)+f(-4)=1,所以-log22+a-log24+a=1,
即2a=1+1+2=4,所以a=2.
13.
6 【解析】因为an+1=2an,即=2,所以{an}是以2为首项、2为公比的等比数列,因此Sn===126,即2n-1=63,2n=64,所以n=6.
14.
1 【解析】因为f′(x)=3ax2+1,所以斜率k=f′(1)=3a+1.又f(1)=a+2,所以切线方程为y-(a+2)=(3a+1)(x-1),所以7-a-2=(3a+1)×1,所以a=1.
15.
4 【解析】作出不等式组表示的可行域如图中阴影部分所示,由目标函数z=3x+y,得y=-3x+z,显然,当直线y=-3x+z经过点B时,在y轴上的截距最大,即z最大.由解得即B(1,1),所以zmax=3×1+1=4.
(第15题)
16.
12 【解析】如图,设F1为双曲线的左焦点,则AF=15,AF=AF1,C△APF=AP+PF+FA=AP+PF+AF1.因为PF-PF1=2a=2,所以PF=PF1+2,所以C△APF=AP+PF1+2+AF1≥AF1+2+AF1,即A,P,F1三点共线时,△APF的周长最小,为32,此时直线lAF1:y=2(x+3).联立解得x=-2,y=2,所以S△APF=S△AF1F-S△PF1F=×6×6-×6×2=12.
(第16题)
17.
(1)
由题设及正弦定理可得b2=2ac.又a=b,可得b=2c,a=2c.
由余弦定理可得cos
B==.
(2)
由题设知b2=2ac.因为B=90°,由勾股定理得a2+c2=b2,
故a2+c2=2ac,得c=a=,所以△ABC的面积为1.
18.
(1)
因为四边形ABCD为菱形,所以AC⊥BD.
因为BE⊥平面ABCD,AC平面ABCD,所以AC⊥BE.
又因为BE∩BD=B,故AC⊥平面BED.
又AC平面AEC,所以平面AEC⊥平面BED.
设AB=x,在菱形ABCD中,由∠ABC=120°,
可得AG=GC=x,GB=GD=.
因为AE⊥EC,所以在Rt△AEC中,可得EG=x.
由BE⊥平面ABCD,知△EBG为直角三角形,可得BE=x.
由已知得,三棱锥E-ACD的体积VE-ACD=×AC·GD·BE=x3=,故x=2.
从而可得AE=EC=ED=,
所以△EAC的面积为3,△EAD的面积与△ECD的面积均为,
故三棱锥EACD的侧面积为3+2.
19.
(1)
由散点图可以判断,y=c+d适宜作为年销售量y关于年宣传费x的回归方程类型.
(2)
令w=,先建立y关于w的线性回归方程,由于=68,
=y-w=563-68×6.8=100.6,
所以y关于w的线性回归方程为=100.6+68w,
因此y关于x的回归方程为=100.6+68.
(3)
①由(2)知,当x=49时,年销售量y的预报值=100.6+68=576.6,
年利润z的预报值=576.6×0.2-49=66.32.
②根据(2)的结果知,年利润z的预报值=0.2(100.6+68)-x=-x+13.6+20.12.
所以当==6.8,即x=46.24时,取得最大值.
故年宣传费为46.24千元时,年利润的预报值最大.
(1)
由题设可知直线l的方程为y=kx+1.
因为l与C交于两点,所以<1,解得
(2)
设M(x1,y1),N(x2,y2).将y=kx+1代入方程(x-2)2+(y-3)2=1,
整理得(1+k2)x2-4(1+k)x+7=0,所以x1+x2=,x1x2=.
·=x1x2+y1y2=(1+k2)x1x2+k(x1+x2)+1=+8.
由题设可得+8=12,解得k=1,所以直线l的方程为y=x+1.
故圆心C在l上,所以MN=2.
21.
(1)
f(x)的定义域为(0,+∞),f′(x)=2e2x-(x>0).
当a≤0时,f′(x)>0,f′(x)没有零点;
当a>0时,因为e2x单调递增,-单调递增,所以f′(x)在(0,+∞)上单调递增.
又f′(a)>0,当b满足0
由(1)可设f′(x)在(0,+∞)上的唯一零点为x0,
当x∈(0,x0)时,f′(x)<0;当x∈(x0,+∞)时,f′(x)>0.
故f(x)在(0,x0)上单调递减,在(x0,+∞)上单调递增,
所以当x=x0时,f(x)取得最小值,最小值为f(x0).
由于2e2x0-=0,所以f(x0)=+2ax0+aln
≥2a+aln
.
故当a>0时,f(x)≥2a+aln
.
(1)
如图,连接AE,由已知得,AE⊥BC,AC⊥AB.
在Rt△AEC中,由已知得DE=DC,
故∠DEC=∠DCE.
连接OE,则∠OBE=∠OEB.
又∠ACB+∠ABC=90°,
所以∠DEC+∠OEB=90°,
故∠OED=90°,DE是圆O的切线.
(2)
设CE=1,AE=x,由已知得AB=2,BE=.
由射影定理可得,AE2=CE·BE,
所以x2=,即x4+x2-12=0,
可得x=,所以∠ACB=60°
(第22题)
.
23.
(1)
因为x=ρcos
θ,y=ρsin
θ,所以C1的极坐标方程为ρcos
θ=-2,C2的极坐标方程为ρ2-2ρcos
θ-4ρsin
θ+4=0.
(2)
将θ=代入ρ2-2ρcos
θ-4ρsin
θ+4=0,得ρ2-3ρ+4=0,解得ρ1=2,
ρ2=,故ρ1-ρ2=,即MN=.
由于C2的半径为1,所以△C2MN的面积为.
24.
(1)
当a=1时,f(x)>1可化为|x+1|-2|x-1|-1>0.
当x≤-1时,不等式化为x-4>0,无解;
当-1
所以f(x)>1的解集为.
(2)
由题设可得,f(x)=
所以函数f(x)的图象与x轴围成的三角形的三个顶点分别为A,B(2a+1,0),C(a,a+1),△ABC的面积为(a+1)2.
由题设得(a+1)2>6,故a>2.
所以实数a的取值范围为(2,+∞).
2016年普通高等学校招生全国统一考试
数学文科(新课标Ⅰ卷)
一、
选择题:本大题共12小题,每小题5分.
1.
设集合A={1,3,5,7},B={x|2≤x≤5},则A∩B等于( )
A.
{1,3}
B.
{3,5}
C.
{5,7}
D.
{1,7}
2.
设(1+2i)(a+i)的实部与虚部相等,其中a为实数,则a等于( )
A.
-3
B.
-2
C.
2
D.
3
3.
为美化环境,从红、黄、白、紫4种颜色的花中任选2种花种在一个花坛中,余下的2种花种在另一个花坛中,则红色和紫色的花不在同一花坛的概率是( )
A.
B.
C.
D.
4.
△ABC的内角A,B,C的对边分别为a,b,c.已知a=,c=2,cos
A=,则b等于( )
A.
B.
C.
2
D.
3
5.
直线l经过椭圆的一个顶点和一个焦点,若椭圆中心到l的距离为其短轴长的,则该椭圆的离心率为( )
A.
B.
C.
D.
6.
将函数y=2sin的图象向右平移个周期后,所得图象对应的函数为( )
A.
y=2sin
B.
y=2sin
C.
y=2sin
D.
y=2sin
7.
如图,某几何体的三视图是三个半径相等的圆及每个圆中两条相互垂直的半径.若
(第7题)
该几何体的体积是,则它的表面积是( )
A.
17π
B.
18π
C.
20π
D.
28π
8.
若a>b>0,0
logac
logca
ac
ca>cb
9.
函数y=2x2-e|x|在[-2,2]上的图象大致为( )
,
,
(B)
(D)
10.
执行如图所示的程序框图,如果输入的x=0,y=1,n=1,则输出x,y的值满足( )
A.
y=2x
B.
y=3x
C.
y=4x
D.
y=5x
(第10题)
11.
平面α过正方体ABCD-A1B1C1D1的顶点A,α∥平面CB1D1,α∩平面ABCD=m,α∩平面ABB1A1=n,则m,n所成角的正弦值为( )
A.
B.
C.
D.
12.
若函数f(x)=x-sin
2x+asin
x在(-∞,+∞)上单调递增,则a的取值范围是( )
A.
[-1,1]
B.
C.
D.
二、
填空题:本大题共4小题,每小题5分.
13.
设向量a=(x,x+1),b=(1,2),且a⊥b,则x=________.
14.
已知θ是第四象限角,且sin=,则tan=_________.
15.
设直线y=x+2a与圆C:x2+y2-2ay-2=0相交于A,B两点,若AB=2,则圆C的面积为________.
16.
某高科技企业生产产品A和产品B需要甲、乙两种新型材料.生产一件产品A需要甲材料1.5
kg,乙材料1
kg,用5个工时;生产一件产品B需要甲材料0.5
kg,乙材料0.3
kg,用3个工时,生产一件产品A的利润为2
100元,生产一件产品B的利润为900元.该企业现有甲材料150
kg,乙材料90
kg,则在不超过600个工时的条件下,生产产品A、产品B的利润之和的最大值为________元.
三、
解答题:解答时应写出必要的文字说明、证明过程或演算步骤.
17.(本小题满分12分)已知{an}是公差为3的等差数列,数列{bn}满足b1=1,b2=,anbn+1+bn+1=nbn.
(1)
求数列{an}的通项公式;
(2)
求数列{bn}的前n项和.
18.
(本小题满分12分)如图,已知正三棱锥P-ABC的侧面是直角三角形,PA=6,顶点P在平面ABC内的正投影为点D,D在平面PAB内的正投影为点E,连接PE并延长交AB于点G.
(1)
求证:G是AB的中点;
(2)
在图中作出点E在平面PAC内的正投影F(说明作法及理由),并求四面体PDEF的体积.
(第18题)
19.
(本小题满分12分)某公司计划购买1台机器,该种机器使用三年后即被淘汰.机器有一易损零件,在购进机器时,可以额外购买这种零件作为备件,每个200元.在机器使用期间,如果备件不足再购买,则每个500元.现需决策在购买机器时应同时购买几个易损零件,为此搜集并整理了100台这种机器在三年使用期内更换的易损零件数,得到如图所示的柱状图.记x表示1台机器在三年使用期内需更换的易损零件数,y表示1台机器在购买易损零件上所需的费用(单位:元),n表示购机的同时购买的易损零件数.
(1)
若n=19,求y与x的函数解析式;
(2)
若要求“需更换的易损零件数不大于n”的频率不小于0.5,求n的最小值;
(3)
假设这100台机器在购机的同时每台都购买19个易损零件,或每台都购买20个易损零件,分别计算这100台机器在购买易损零件上所需费用的平均数,以此作为决策依据,购买1台机器的同时应购买19个还是20个易损零件?
(第19题)
20.
(本小题满分12分)在直角坐标系xOy中,直线l:y=t(t≠0)交y轴于点M,交抛物线C:y2=2px(p>0)于点P,M关于点P的对称点为N,连接ON并延长交C于点H.
(1)
求;
(2)
除H以外,直线MH与C是否有其他公共点?请说明理由.
21.
(本小题满分12分)已知函数f(x)=(x-2)ex+a(x-1)2.
(1)
讨论f(x)的单调性;
(2)
若f(x)有两个零点,求a的取值范围.
请考生在第22,23,24题中任选一题作答,如果多做,则按所做的第一题计分.
22.
(本小题满分10分)选修41:几何证明选讲
如图,△OAB是等腰三角形,∠AOB=120°.以O为圆心,OA为半径作圆.
(1)
求证:直线AB与圆O相切;
(2)
点C,D在圆O上,且A,B,C,D四点共圆,求证:AB∥CD.
(第22题)
23.
(本小题满分10分)选修44:坐标系与参数方程
在直角坐标系xOy中,曲线C1的参数方程为(t为参数,a>0).在以坐标原点为极点,x轴正半轴为极轴的极坐标系中,曲线C2:ρ=4cos
θ.
(1)
说明C1是哪种曲线,并将C1的方程化为极坐标方程;
(2)
直线C3的极坐标方程为θ=α0,其中α0满足tan
α0=2,若曲线C1与C2的公共点都在C3上,求a.
24.
(本小题满分10分)选修45:不等式选讲
已知函数f(x)=|x+1|-|2x-3|.
(1)
画出y=f(x)的图象;
(2)
求不等式|f(x)|>1的解集.
(第24题)
2016年普通高等学校招生全国统一考试
数学文科(新课标Ⅰ卷)
1.
B 【解析】集合A与集合B的公共元素为3,5,所以A∩B={3,5},故选B.
2.
A 【解析】(1+2i)(a+i)=a-2+(1+2a)i,由已知,得a-2=1+2a,解得a=-3.故选A.
3.
C 【解析】将4种颜色的花种任选两种种在一个花坛中,余下2种种在另一个花坛,有6种种法,其中红色和紫色的花不在一个花坛的种法有4种,故所求概率为.故选C.
4.
D 【解析】由余弦定理得5=b2+4-2×b×2×,解得b=3,b=-(舍去).故选D.
5.
B 【解析】如图,由题意得在椭圆中,OF=c,OB=b,OD=×2b=b,BF=a,在Rt△OFB中,OF×OB=BF×OD,即cb=,所以c=,所以椭圆的离心率e=.故选B.
(第5题)
6.
D 【解析】函数y=2sin的周期为π,将函数y=2sin(2x+)的图象向右平移个周期即个单位长度,得到函数y=2sin[2(x-)+]=2sin的图象.故选D.
7.
A 【解析】由三视图可知该几何体为一个切去了部分的球,设球的半径为r,则×=,解得r=2.此几何体的表面积应为个球面面积加上3个圆面积之和,所以表面积为(4πr2)×+3×=17π.故选A.
8.
B 【解析】对于选项A:logac=,logbc=,因为0
a>lg
b,但不能确定lg
a,lg
b的正负,所以它们的大小不能确定;对于选项B:logca=,logcb=,而lg
a>lg
b,两边同乘以一个负数改变不等号方向,所以选项B正确;对于选项C:利用y=xc在第一象限内是增函数可得ac>bc,所以C错误;对于选项D:利用y=cx在R上为减函数易得D错误.故选B.
9.
D 【解析】函数y=f(x)=2x2-e|x|在[-2,2]上是偶函数,其图象关于y轴对称,因为f(2)=8-e2,0<8-e2<1,所以排除A,B选项;当x∈[0,2]时,y′=4x-ex有一零点,设为x0,当x∈(0,x0)时,f(x)为减函数,当x∈(x0,2)时,f(x)为增函数.故选D.
10.
C 【解析】第一次循环:x=0,y=1,第二次循环:n=2,x=,y=2,第三次循环:n=3,x=,y=6,此时满足条件x2+y2≥36,结束循环,输出x=,y=6,满足y=4x.故选C.
11.
A 【解析】如图,因为α∥平面CB1D1,设平面CB1D1∩平面ABCD=m1,则
m1∥m.又因为平面ABCD∥平面A1B1C1D1,平面B1D1C∩平面A1B1C1D1=B1D1,所以B1D1∥m1,故B1D1∥m.同理可得CD1∥n.故m,n所成角的大小与B1D1,CD1所成角的大小相等,即为∠CD1B1的大小.而B1C=B1D1=CD1(均为面对角线),因此∠CD1B1=,即sin∠CD1B1=.故选A.
(第11题)
12.
C 【解析】用特殊值法:取a=-1,则f(x)=x-sin
2x-sin
x,f′(x)=1-cos
2x-cos
x,因为f′(0)=1--1=-<0,所以f(x)不可能在(-∞,+∞)上单调递增,排除A,B,D.故选C.
13.
- 【解析】由题意知a·b=0,x+2(x+1)=0,所以x=-.
14.
-
【解析】由题意得cos=,则tan=,所以tan=tan(θ+-)=-=-.
15.
4π 【解析】圆C:x2+y2-2ay-2=0,即C:x2+(y-a)2=a2+2,圆心为C(0,a),由AB=2,圆心C到直线y=x+2a的距离为,得+=a2+2,解得a2=2,所以圆C的面积为π(a2+2)=4π.
16.
216
000 【解析】设生产产品A、产品B分别为x,y件,利润之和为z元,目标函数z=2
100x+900y.由题意得即
作出可行域如图中阴影部分所示,
将z=2
100x+900y变形,得y=-x+,平移直线y=-x,当直线y=-x+经过点M时,z
取得最大值.由得点M的坐标为(60,100).所以当x=60,y=100时,zmax=2
100×60+900×100=216
000.经检验,符合题意.
(第16题)
17.
(1)
由已知得a1b2+b2=b1,又b1=1,b2=,得a1=2,
所以数列{an}是首项为2、公差为3的等差数列,
其通项公式为an=3n-1.
由(1)及anbn+1+bn+1=nbn,得bn+1=,
因此{bn}是首项为1、公比为的等比数列,设{bn}的前n项和为Sn,
则Sn==-.
18.
(1)
因为P在平面ABC内的正投影为D,所以AB⊥PD.
因为D在平面PAB内的正投影为E,所以AB⊥DE.
因为DE∩PD=D,所以AB⊥平面PED,故AB⊥PG.
又由已知可得PA=PB,从而G是AB的中点.
(第18题)
(2)
如图,在平面PAB内,过点E作PB的平行线交PA于点F,F即为E在平面PAC内的正投影.
理由如下:由已知可得PB⊥PA,PB⊥PC,又EF∥PB,所以EF⊥PA,EF⊥PC,又PA∩PC=P,所以EF⊥平面PAC,即点F为E在平面PAC内的正投影.
连接CG,因为P在平面ABC内的正投影为D,
所以D是正三角形ABC的中心.
由(1)知G是AB的中点,所以D在CG上,且CD=CG.
由题设可得PC⊥平面PAB,DE⊥平面PAB,
所以DE∥PC,因此PE=PG,DE=PC.
由已知,正三棱锥的侧面是直角三角形且PA=6,
所以DE=2,PE=2.
在等腰直角三角形EFP中,可得EF=PF=2,
所以四面体PDEF的体积V=S△EFP·DE=××2×2×2=.
19.
(1)
当x≤19时,y=3
800;
当x>19时,y=3
800+500(x-19)=500x-5
700.
所以y与x的函数解析式为
y=(x∈N).
(2)
由柱状图知,需更换的零件数不大于18的频率为0.46,不大于19的频率为0.7,故n的最小值为19.
(3)
若每台机器在购机同时都购买19个易损零件,则这100台机器中有70台在购买易损零件上的费用为3
800元,20台的费用为4
300元,10台的费用为4
800元,因此这100台机器在购买易损零件上所需费用的平均数为×(3
800×70+4
300×20+4
800×10)=4
000.
若每台机器在购机同时都购买20个易损零件,则这100台机器中有90台在购买易损零件上的费用为4
000元,10台的费用为4
500元,因此这100台机器在购买易损零件上所需费用的平均数为×(4
000×90+4
500×10)=4
050.
比较两个平均数可知,购买1台机器的同时应购买19个易损零件.
20.
(1)
由已知得M(0,t),P.
又N为M关于点P的对称点,故N,ON的方程为y=x,代入y2=2px,整理得px2-2t2x=0,解得x1=0,x2=,因此H,
所以N为OH的中点,即=2.
(2)
直线MH与C除H以外没有其他公共点,理由如下:
由(1)知直线MH的方程为y-t=x,即x=(y-t).
代入y2=2px得y2-4ty+4t2=0,解得y1=y2=2t,即直线MH与C只有一个公共点,所以除H以外直线MH与C没有其他公共点.
21.
(1)
f′(x)=(x-1)ex+2a(x-1)=(x-1)(ex+2a).
若a≥0,则当x∈(-∞,1)时,f′(x)<0;当x∈(1,+∞)时,f′(x)>0,
所以f(x)在(-∞,1)上单调递减,在(1,+∞)上单调递增.
若a<0,由f′(x)=0,得x=1或x=ln(-2a).
①当a=-时,则f′(x)=(x-1)(ex-e)≥0,
所以f(x)在(-∞,+∞)上单调递增.
②当a>-时,则ln(-2a)<1,故当x∈(-∞,ln(-2a))∪(1,+∞)时,f′(x)>0;当x∈(ln(-2a),1)时,f′(x)<0,所以f(x)在(-∞,ln(-2a)),(1,+∞)上单调递增,在(ln(-2a),1)上单调递减.
③当a<-时,则ln(-2a)>1,故当x∈(-∞,1)∪(ln(-2a),+∞)时,f′(x)>0;当x∈(1,ln(-2a))时,f′(x)<0,
所以f(x)在(-∞,1),(ln(-2a),+∞)上单调递增,在(1,ln(-2a))上单调递减.
(2)
①若a>0,则由(1)知f(x)在(-∞,1)上单调递减,在(1,+∞)上单调递增.
又f(1)=-e,f(2)=a,取b满足b<0且b<ln,
则f(b)>(b-2)+a(b-1)2=a>0,所以f(x)有两个零点.
②若a=0,则f(x)=(x-2)ex,所以f(x)只有一个零点.
③若a<0,当a≥-时,则由(1)知f(x)在(1,+∞)上单调递增,又当x≤1时f(x)<0,故f(x)不存在两个零点;
当a<-时,则由(1)知f(x)在(1,ln(-2a))上单调递减,在(ln(-2a),+∞)上单调递增,又当x≤1时f(x)<0,故f(x)不存在两个零点.
综上,a的取值范围为(0,+∞).
22.
(1)
如图,设E是AB的中点,连接OE.
因为OA=OB,∠AOB=120°,所以OE⊥AB,∠AOE=60°.
在Rt△AOE中,OE=AO,即点O到直线AB的距离等于圆O的半径,
所以直线AB与圆O相切.
(第22题)
(2)
因为OA=2OD,所以O不是A,B,C,D四点所在圆的圆心.
如图,设O′是A,B,C,D四点所在圆的圆心,作直线OO′.
由已知得O在线段AB的垂直平分线上,
又O′在线段AB的垂直平分线上,所以OO′⊥AB.
同理可证OO′⊥CD,所以AB∥CD.
23.
(1)
消去参数t得到C1的普通方程为x2+(y-1)2=a2,
故C1是以(0,1)为圆心,a为半径的圆.
将x=ρcos
θ,y=ρsin
θ代入C1的普通方程中,得C1的极坐标方程为ρ2-2ρsin
θ+1-a2=0.
(2)
曲线C1,C2的公共点的极坐标满足方程组
若ρ≠0,由方程组得16cos2
θ-8sin
θcos
θ+1-a2=0.
由已知tan
θ=2,可得16cos2
θ-8sin
θcos
θ=0,
从而1-a2=0,解得a=-1(舍去)或a=1.
当a=1时,极点为C1,C2的公共点,且在C3上,
所以a=1.
24.
(1)
f(x)=y=f(x)的图象如图所示.
(第24题)
(2)
由|f(x)|>1得f(x)>1或f(x)<-1.当f(x)=1时,可得x=1或x=3;
当f(x)=-1时,可得x=或x=5.
由y=f(x)的图象知f(x)>1的解集为{x|1<x<3},f(x)<-1的解集为.
所以|f(x)|>1的解集为.
2017年普通高等学校招生全国统一考试
数学文科(新课标Ⅰ卷)
一、
选择题:本大题共12小题,每小题5分.
1.
已知集合A={x|x<2},B={x|3-2x>0},那么( )
A.
A∩B=
B.
A∩B=
C.
A∪B=
D.
A∪B=R
2.
为评估一种农作物的种植效果,选了n块地作试验田.这n块地的亩产量(单位:kg)分别为x1,x2,…,xn,下面给出的指标中可以用来评估这种农作物亩产量稳定程度的是( )
A.
x1,x2,…,xn的平均值
B.
x1,x2,…,xn的标准差
C.
x1,x2,…,xn的最大值
D.
x1,x2,…,xn的中位数
3.
下列各式的运算结果为纯虚数的是( )
A.
i(1+i)2
B.
i2(1-i)
C.
(1+i)2
D.
i(1+i)
4.
如图,正方形ABCD内的图形来自中国古代的太极图.正方形内切圆中的黑色部分和白色部分关于正方形的中心成中心对称.若在正方形内随机取一点,则此点取自黑色部分的概率是( )
A.
B.
C.
D.
(第4题)
5.
已知F是双曲线C:x2-=1的右焦点,P是C上一点,且PF与x轴垂直,点A的坐标是(1,3),那么△APF的面积为( )
A.
B.
C.
D.
6.
如图,在下列四个正方体中,若A,B为正方体的两个顶点,M,N,Q为所在棱的中点,则在这四个正方体中,直线AB与平面MNQ不平行的是( )
若x,y满足约束条件则z=x+y的最大值为( )
A.
0
B.
1
C.
2
D.
3
8.
函数y=的部分图象大致为( )
9.
已知函数f(x)=lnx+ln(2-x),那么( )
A.
f(x)在(0,2)上单调递增
B.
f(x)在(0,2)上单调递减
C.
y=f(x)的图象关于直线x=1对称
D.
y=-f(x)的图象关于点(1,0)对称
10.
如图所示的程序框图是为了求出满足3n-2n>1
000的最小偶数n,那么在和两个空白框中,可以分别填入( )
A.
A>1
000和n=n+1
B.
A>1
000和n=n+2
C.
A≤1
000和n=n+1
D.
A≤1
000和n=n+2
(第10题)
11.
已知△ABC的内角A,B,C的对边分别为a,b,c.若sinB+sinA(sinC-cosC)=0,a=2,c=,则角C等于( )
A.
B.
C.
D.
12.
已知A,B是椭圆C:+=1长轴的两个端点.若C上存在点M满足∠AMB=120°,则m的取值范围是( )
A.
(0,1]∪[9,+∞)
B.
(0,]∪[9,+∞)
C.
(0,1]∪[4,+∞)
D.
(0,]∪[4,+∞)
二、
填空题:本大题共4小题,每小题5分.
13.
已知向量a=(-1,2),b=(m,1).若向量a+b与a垂直,则m=________.
14.
曲线y=x2+在点(1,2)处的切线方程为________.
15.
已知α∈,tanα=2,那么cos=________.
16.
已知三棱锥S-ABC的所有顶点都在球O的球面上,SC是球O的直径.若平面SCA⊥平面SCB,SA=AC,SB=BC,三棱锥S-ABC的体积为9,则球O的表面积为________.
三、
解答题:解答时应写出必要的文字说明、证明过程或演算步骤.
17.
(本小题满分12分)记Sn为等比数列{an}的前n项和.已知S2=2,S3=-6.
(1)
求{an}的通项公式;
(2)
求Sn,并判断Sn+1,Sn,Sn+2是否成等差数列.
18.
(本小题满分12分)如图,在四棱锥P-ABCD中,AB∥CD,且∠BAP=∠CDP=90°.
(1)
求证:平面PAB⊥平面PAD;
(2)
若PA=PD=AB=DC,∠APD=90°,且四棱锥P-ABCD的体积为,求该四棱锥的侧面积.
(第18题)
19.
(本小题满分12分)为了监控某种零件的一条生产线的生产过程,检验员每隔30
min从该生产线上随机抽取一个零件,并测量其尺寸(单位:cm).下面是检验员在一天内依次抽取的16个零件的尺寸:
抽取次序
1
2
3
4
5
6
7
8
零件尺寸
9.95
10.12
9.96
9.96
10.01
9.92
9.98
10.04
抽取次序
9
10
11
12
13
14
15
16
零件尺寸
10.26
9.91
10.13
10.02
9.22
10.04
10.05
9.95
(1)
求(xi,i)(i=1,2,…,16)的相关系数r,并回答是否可以认为这一天生产的零件尺寸不随生产过程的进行而系统地变大或变小(若|r|<0.25,则可以认为零件的尺寸不随生产过程的进行而系统地变大或变小).
(2)
在一天内抽检的零件中,如果出现了尺寸在(x-3s,x+3s)之外的零件,就认为这条生产线在这一天的生产过程可能出现了异常情况,需对当天的生产过程进行检查.
①从这一天抽检的结果看,是否需对当天的生产过程进行检查?
②在(x-3s,x+3s)之外的数据称为离群值,试剔除离群值,估计这条生产线当天生产的零件尺寸的均值与标准差.(精确到0.01)
附:样本(xi,yi)(i=1,2,…,n)的相关系数为
r=,
≈0.09.
20.
(本小题满分12分)设A,B为曲线C:y=上两点,A与B的横坐标之和为4.
(1)
求直线AB的斜率;
(2)
设M为曲线C上一点,C在M处的切线与直线AB平行,且AM⊥BM,求直线AB的方程.
21.
(本小题满分12分)已知函数f(x)=ex(ex-a)-a2x.
(1)
讨论f(x)的单调性;
(2)
若f(x)≥0,求a的取值范围.
请考生在第22,23题中任选一题作答,如果多做,则按所做的第一题计分.
22.
(本小题满分10分)选修44:坐标系与参数方程
在直角坐标系xOy中,曲线C的参数方程为(θ为参数),直线l的参数方程为(t为参数).
(1)
若a=-1,求C与l的交点坐标;
(2)
若C上的点到l距离的最大值为,求a的值.
23.
(本小题满分10分)选修45:不等式选讲
已知函数f(x)=-x2+ax+4,g(x)=|x+1|+|x-1|.
(1)
当a=1时,求不等式f(x)≥g(x)的解集;
(2)
若不等式f(x)≥g(x)的解集包含[-1,1],求a的取值范围.
2017年普通高等学校招生全国统一考试
数学文科(新课标Ⅰ卷)
1.
A 【解析】由题意得B=,从而A∩B=,A∪B={x|x<2}.故选A.
2.
B 【解析】在样本的几个特征量中,平均数反映集中趋势,标准差反映起伏大小,中位数不会因个别数据的异常发生改变,极差是最大值和最小值的差,一般用来制作频率分布直方图.故选B.
3.
C 【解析】因为i(1+i)2=2i2=-2,i2(1-i)=-1+i,(1+i)2=2i,i(1+i)=-1+i,由纯虚数的定义知选C.故选C.
4.
B 【解析】设正方形的边长为2,由该图形的中心对称性知图中黑色部分的面积为,又正方形的面积为4,所以P==.故选B.
5.
D 【解析】依题意,点F的坐标为(2,0),点P的坐标为(2,3),所以△PAF的面积为S=AP·PF=×1×3=.故选D.
6.
A 【解析】如图(1),O为BC的中点,连接OQ,易知AB∥OQ,OQ与平面MNQ显然不平行,故AB与平面MNQ不平行;B中,AB∥MQ,从而AB∥平面MNQ;C中,如图(2),C为AD的中点,易得AB∥CN,CN∥MQ,显然AB?平面MNQ,故AB∥平面MNQ;D中,显然NQ∥AB,又AB?平面MNQ,故AB∥平面MNQ.故选A.
图(1)
图(2)
(第6题)
7.
D 【解析】作出可行域如图中阴影部分所示,平移直线y=-x+z,可知z=x+y在点A(3,0)处取得最大值,即zmax=3.故选D.
(第7题)
C 【解析】设f(x)=,由f(x)+f(-x)=0知f(x)为奇函数,故排除B.由f(1)>0,可排除A;由f(π)=0,可排除D.故选C.
9.
C 【解析】由题易知,f(x)的定义域为(0,2),且f(x)=ln(-x2+2x),由复合函数单调性易判断f(x)在(0,1)上单调递增,在(1,2)上单调递减,所以选项A,B错误;又因为f(2-x)=ln(2-x)+ln[2-(2-x)]=ln(2-x)+lnx=f(x),所以f(x)的图象关于直线x=1对称,所以D选项错误,C正确.故选C.
10.
D 【解析】由n为偶数可知,执行框中应为n=n+2,又因为3n-2n>1
000时结束循环,因此,判断框中应为A≤1
000.故选D.
11.
B 【解析】因为sinB+sinA(sinC-cosC)=sin(A+C)+sinAsinC-sinAcosC=sinAcosC+cosAsinC+sinAsinC-sinAcosC=sinC(cosA+sinA)=0,因为sinC≠0,所以cosA+sinA=0,可解得A=,由正弦定理可得sinC==.又C∈,所以C=.故选B.
12.
A 【解析】若m<3,如图(1),易知点M在y轴上时,∠AMB取得最大值120°,此时∠MBO=30°,tan∠MBO===,解得m=1,故短轴长只能小于此边界情况才能满足题意,所以m∈(0,1].若m>3,如图(2),当M在x轴上时,∠AMB取最大值120°,同理可得tan30°===,所以m=9,当m≥9时,才能满足题意.综上,m∈(0,1]∪[9,+∞).故选A.
图(1)
图(2)
(第12题)
13.
7 【解析】由题意得,(a+b)·a=0,即a2+a·b=0,即5-m+2=0,解得m=7.
14.
y=x+1 【解析】由题意知y′=2x-,当x=1时,y′=1,y=2,从而切线的方程是y=x+1.
15.
【解析】由α∈,tanα=2,得sinα=,cosα=,从而cos=cosαcos+sinαsin=×+×=.
16.
36π 【解析】如图,O为球心,连接AO,BO,设SA=a,半径为R.因为SB=BC,所以BO⊥SC,又因为平面SCA⊥平面SCB,所以BO⊥平面SAC.因为SA=AC,SC是直径,所以BO=AO=a=SO,从而VS
ABC=·BO·S△ASC=×a×=9,解得a=3,从而R=a=3,球O的表面积为4πR2=36π.
(第16题)
17.
(1)
设{an}的公比为q,由题设可得解得q=-2,a1=-2.
故{an}的通项公式为an=(-2)n.
(2)
由(1)可得Sn==-+.
由于Sn+2+Sn+1=-+=2=2Sn,
故Sn+1,Sn,Sn+2成等差数列.
(1)
由已知∠BAP=∠CDP=90°,得AB⊥AP,CD⊥PD.
因为AB∥CD,所以AB⊥PD,
又AP∩PD=P,从而AB⊥平面PAD.
因为AB平面PAB,所以平面PAB⊥平面PAD.
(第18题)
(2)
如图,过点P作PE⊥AD,垂足为E.由(1)知,AB⊥平面PAD,故AB⊥PE,可得PE⊥平面ABCD.设AB=x,则由已知可得AD=x,PE=x.
故四棱锥P-ABCD的体积VP
-
ABCD=AB·AD·PE=x3.
由题设得x3=,故x=2,
从而PA=PD=2,AD=BC=2,PB=PC=2,
可得四棱锥P-ABCD的侧面积为
PA·PD+PA·AB+PD·DC+BC2sin60°=6+2.
19.
(1)
由样本数据得(x,i)(i=1,2,…,16)的相关系数为
r==≈-0.18.
由于|r|<0.25,因此可以认为这一天生产的零件尺寸不随生产过程的进行而系统地变大或变小.
(2)
①由于x=9.97,s≈0.212,由样本数据可以看出抽取的第13个零件的尺寸在(x-3s,x+3s)以外,因此需对当天的生产过程进行检查.
②剔除离群值,即第13个数据,剩下数据的平均数为
σ2=(16×9.97-9.22)=10.02,
这条生产线当天生产的零件尺寸的均值的估计值为10.02.
=16×0.2122+16×9.972≈1
591.134,
剔除第13个数据,剩下数据的样本方差为
(1
591.134-9.222-15×10.022)≈0.008,
故这条生产线当天生产的零件尺寸的标准差的估计值为≈0.09.
20.
(1)
设A(x1,y1),B(x2,y2),
则x1≠x2,y1=,y2=,x1+x2=4,
于是直线AB的斜率k===1.
(2)
由y=,得y′=,
设M(x3,y3),由题设知=1,解得x3=2,于是M(2,1).
设直线AB的方程为y=x+m,
故线段AB的中点为N(2,2+m),MN=|m+1|.
将y=x+m代入y=得x2-4x-4m=0.
当Δ=16(m+1)>0,即m>-1时,x1,2=2±2,
从而AB=|x1-x2|=4.
由题设知AB=2MN,即4=2(m+1),解得m=7,
所以直线AB的方程为y=x+7.
21.
(1)
函数f(x)的定义域为(-∞,+∞),f′(x)=2e2x-aex-a2=(2ex+a)(ex-a).
①若a=0,则f(x)=e2x,在(-∞,+∞)上单调递增.
②若a>0,则由f′(x)=0得x=lna.
当x∈(-∞,lna)时,f′(x)<0;当x∈(lna,+∞)时,f′(x)>0.
故f(x)在(-∞,lna)上单调递减,在(lna,+∞)上单调递增.
③若a<0,则由f′(x)=0得x=ln.
当x∈时,f′(x)<0;当x∈(ln,+∞)时,f′(x)>0.故f(x)在上单调递减,在上单调递增.
(2)
①若a=0,则f(x)=e2x,所以f(x)≥0.
②若a>0,则由(1)得,当x=lna时,f(x)取得最小值,最小值为f(lna)=-a2lna,当且仅当-a2lna≥0,即0
综上,a的取值范围是[-2e,1].
22.
(1)
曲线C的普通方程为+y2=1.
当a=-1时,直线l的普通方程为x+4y-3=0.
由解得或
从而C与l的交点坐标为(3,0),.
直线l的普通方程为x+4y-a-4=0,
故C上的点(3cosθ,sinθ)到l的距离为d=.
当a≥-4时,d的最大值为
.由题设得=,所以a=8.
当a<-4时,d的最大值为.由题设得=,所以a=-16.
综上,a=8或a=-16.
23.
(1)
当a=1时,不等式f(x)≥g(x)等价于
x2-x+|x+1|+|x-1|-4≤0. ①
当x<-1时,①式化为x2-3x-4≤0,无解;
当-1≤x≤1时,①式化为x2-x-2≤0,从而-1≤x≤1;
当x>1时,①式化为x2+x-4≤0,从而1
(2)
当x∈[-1,1]时,g(x)=2.
所以f(x)≥g(x)的解集包含[-1,1],等价于当x∈[-1,1]时f(x)≥2.
又f(x)在[-1,1]上的最小值必为f(-1)与f(1)之一,
所以f(-1)≥2且f(1)≥2,得-1≤a≤1.
所以a的取值范围为[-1,1].
2018年普通高等学校招生全国统一考试
数学文科(新课标Ⅰ卷)
一、
选择题:本大题共12小题,每小题5分.
1.
已知集合A={0,2},B={-2,-1,0,1,2},则A∩B等于( )
A.
{0,2}
B.
{1,2}
C.
{0}
D.
{-2,-1,0,1,2}
2.
设z=+2i,则|z|等于( )
A.
0
B.
C.
1
D.
3.
某地区经过一年的新农村建设,农村的经济收入增加了一倍,实现翻番.为更好地了解该地区农村的经济收入变化情况,统计了该地区新农村建设前后农村的经济收入构成比例,得到如下饼图:
(第3题)
则下面结论中不正确的是( )
A.
新农村建设后,种植收入减少
B.
新农村建设后,其他收入增加了一倍以上
C.
新农村建设后,养殖收入增加了一倍
D.
新农村建设后,养殖收入与第三产业收入的总和超过了经济收入的一半
4.
已知椭圆C:+=1的一个焦点为(2,0),则C的离心率为( )
A.
B.
C.
D.
5.
已知圆柱的上、下底面的中心分别为O1,O2,过直线O1O2的平面截该圆柱所得的截面是面积为8的正方形,则该圆柱的表面积为( )
A.
12π
B.
12π
C.
8π
D.
10π
6.
设函数f(x)=x3+(a-1)x2+ax,若f(x)为奇函数,则曲线y=f(x)在点(0,0)处的切线方程为( )
A.
y=-2x
B.
y=-x
C.
y=2x
D.
y=x
7.
在△ABC中,AD为BC边上的中线,E为AD的中点,则等于( )
A.
-
B.
-
C.
+
D.
+
8.
已知函数f(x)=2cos2x-sin2x+2,则( )
A.
f(x)的最小正周期为π,最大值为3
B.
f(x)的最小正周期为π,最大值为4
C.
f(x)的最小正周期为2π,最大值为3
D.
f(x)的最小正周期为2π,最大值为4
9.
某圆柱的高为2,底面周长为16,其三视图如图所示.圆柱表面上的点M在正视图上的对应点为A,圆柱表面上的点N在侧视图上的对应点为B,则在此圆柱侧面上,从M到N的路径中,最短路径的长度为( )
A.
2
B.
2
C.
3
D.
2
(第9题)
10.
在长方体ABCD-A1B1C1D1中,AB=BC=2,AC1与平面BB1C1C所成的角为30°,则该长方体的体积为( )
A.
8
B.
6
C.
8
D.
8
11.
已知角α的顶点为坐标原点,始边与x轴的非负半轴重合,终边上有两点A(1,a),B(2,b),且cos2α=,则|a-b|等于( )
A.
B.
C.
D.
1
12.
设函数f(x)=则满足f(x+1)
(-∞,-1]
B.
(0,+∞)
C.
(-1,0)
D.
(-∞,0)
填空题:本大题共4小题,每小题5分.
13.
已知函数f(x)=log2(x2+a),若f(3)=1,则a=________.
14.
若x,y满足约束条件则z=3x+2y的最大值为________.
15.
若直线y=x+1与圆x2+y2+2y-3=0交于A,B两点,则AB=________.
16.
已知△ABC的内角A,B,C的对边分别为a,b,c,bsinC+csinB=4asinBsinC,b2+c2-a2=8,则△ABC的面积为________.
三、
解答题:解答时应写出必要的文字说明、证明过程或演算步骤.
17.
(本小题满分12分)已知数列{an}满足a1=1,nan+1=2(n+1)an,设bn=.
(1)
求b1,b2,b3的值;
(2)
判断数列{bn}是否为等比数列,并说明理由;
(3)
求{an}的通项公式.
18.
(本小题满分12分)如图,在平行四边形ABCM中,AB=AC=3,∠ACM=90°,以AC为折痕将△ACM折起,使点M到达点D的位置,且AB⊥DA.
(1)
求证:平面ACD⊥平面ABC;
(2)
若Q为线段AD上一点,P为线段BC上一点,且BP=DQ=DA,求三棱锥Q-ABP的体积.
(第18题)
19.
(本小题满分12分)某家庭记录了未使用节水龙头50天的日用水量数据(单位:m3)和使用了节水龙头50天的日用水量数据,得到频数分布表如下:
未使用节水龙头50天的日用水量频数分布表
日用
水量
[0,0.1)
[0.1,0.2)
[0.2,0.3)
[0.3,0.4)
[0.4,0.5)
[0.5,0.6)
[0.6,0.7)
频数
1
3
2
4
9
26
5
使用了节水龙头50天的日用水量频数分布表
日用水量
[0,0.1)
[0.1,0.2)
[0.2,0.3)
[0.3,0.4)
[0.4,0.5)
[0.5,0.6)
频数
1
5
13
10
16
5
(1)
作出使用了节水龙头50天的日用水量数据的频率分布直方图;
(2)
估计该家庭使用节水龙头后,日用水量小于0.35
m3的概率;
(3)
估计该家庭使用节水龙头后,一年能节省多少水?(一年按365天计算,同一组中的数据以这组数据所在区间中点的值作代表).
(第19题)
20.
(本小题满分12分)设抛物线C:y2=2x,点A(2,0),B(-2,0),过点A的直线l与C交于M,N两点.
(1)
当l与x轴垂直时,求直线BM的方程;
(2)
求证:∠ABM=∠ABN.
21.
(本小题满分12分)已知函数f(x)=aex-lnx-1.
(1)
设x=2是f(x)的极值点,求a的值和f(x)的单调区间;
(2)
求证:当a≥时,f(x)≥0.
请考生在第22,23题中任选一题作答,如果多做,则按所做的第一题计分.
22.
(本小题满分10分)选修44:坐标系与参数方程
在直角坐标系xOy中,曲线C1的方程为y=k|x|+2.以坐标原点为极点,x轴正半轴为极轴建立极坐标系,曲线C2的极坐标方程为ρ2+2ρcosθ-3=0.
(1)
求C2的直角坐标方程;
(2)
若C1与C2有且仅有三个公共点,求C1的方程.
23.
(本小题满分10分)选修45:不等式选讲
已知f(x)=|x+1|-|ax-1|.
(1)
当a=1时,求不等式f(x)>1的解集;
(2)
若x∈(0,1)时不等式f(x)>x成立,求a的取值范围.
2018年普通高等学校招生全国统一考试
数学文科(新课标Ⅰ卷)
1.
A 【解析】A∩B={0,2}.故选A.
2.
C 【解析】因为z=+2i=+2i=-i+2i=i,所以|z|=1.故选C.
3.
A 【解析】假设新农村建设前农村的经济收入为a,新农村建设后,农村的经济收入增加了一倍,实现翻番为2a,所以种植收入为37%×2a=74%a>60%a,故A错.故选A.
4.
C 【解析】在椭圆中,a===2,所以离心率e==.故选C.
5.
B 【解析】设圆柱底面半径为r,则(2r)·(2r)=4r2=8,解得r=,所以该圆柱的表面积为S=(2πr)·(2r)+2πr2=12π.故选B.
6.
D 【解析】因为f(x)为奇函数,所以a-1=0,即a=1,所以f(x)=x3+x,则f′(x)=3x2+1,则曲线y=f(x)在点(0,0)处的切线方程为y-0=f′(0)(x-0),即y=x.故选D.
7.
A 【解析】=+=-=·(+)-(-)=-.故选A.
8.
B 【解析】f(x)=1+cos2x-+2=cos2x+,故最小正周期为π,最大值为+=4.故选B.
9.
B 【解析】根据题意,圆柱的侧面展开图是长为16,宽为2的长方形MDEF,如图,由其三视图可知,点A对应长方形MDEF中的点M,点B为DE上靠近D点的四等分点.则AB的最短路径为线段AB==2.故选B.
(第9题)
10.
C 【解析】如图,设CC1=c,由题易知∠AC1B=30°,则tan∠AC1B===,解得c=2,所以体积V=2×2×2=8.故选C.
(第10题)
B 【解析】由题意知tanα=a=,而cos2α====,所以a2=,所以|a-b|=|a|=.故选B.
12.
D 【解析】画出f(x)的图象,观察图象分析可知存在两种情况:①2x
13.
-7 【解析】因为f(3)=log2(32+a)=1,解得a+9=2,所以a=-7.
14.
6 【解析】作出可行域如图中阴影部分所示,由图可知目标函数z在点(2,0)处取得最大值,为6.
(第14题)
15.
2 【解析】圆x2+y2+2y-3=0化为标准方程为x2+(y+1)2=4,所以圆心为(0,-1),半径为2,圆心到直线y=x+1的距离d==,所以AB=2=2=2.
16.
【解析】由正弦定理得2sinBsinC=4sinAsinBsinC,因为sinB·sinC≠0,所以sinA=.又因为2bccosA=b2+c2-a2=8,所以A为锐角,所以cosA=,所以bc=,所以△ABC的面积S=bcsinA=.
17.
(1)
由条件可得an+1=an.
将n=1代入,得a2=4a1,而a1=1,所以a2=4.
将n=2代入,得a3=3a2,所以a3=12.
从而b1=1,b2=2,b3=4.
(2)
{bn}是首项为1,公比为2的等比数列.
由条件可得=,即bn+1=2bn,又b1=1,
所以{bn}是首项为1,公比为2的等比数列.
(3)
由(2)可得=2n-1,所以an=n·2n-1.
18.
(1)
由已知可得∠BAC=90°,所以AB⊥AC.
又AB⊥AD,AD∩AC=A,所以AB⊥平面ACD.
因为AB平面ABC,所以平面ACD⊥平面ABC.
(第18题)
(2)
由已知可得,DC=CM=AB=AC=3,所以DA=3.
又BP=DQ=DA,所以BP=2.
如图,过点Q作QE⊥AC,垂足为E,则QE∥DC且QE=DC.
由已知及(1)可得DC⊥平面ABC,所以QE⊥平面ABC,QE=1.
因此,三棱锥Q-ABP的体积为VQ
-
ABP=×QE×S△ABP=×1××3×2sin45°=1.
19.
(1)
如图所示.
(第19题)
(2)
由题可知,日用水量在[0.3,0.4)之间的天数为10天,所以可估计在[0.3,0.35)的天数为5天,所以估计日用水量小于0.35
m3的概率为=0.48.
(3)
由题可知,50天的节约水量为(0.05×1+0.15×3+0.25×2+0.35×4+0.45×9+0.55×26+0.65×5)-(0.05×1+0.15×5+0.25×13+0.35×10+0.45×16+0.55×5)=6.5,一年的节约用水量为×6.5=47.45,所以一年能节约47.45
m3水.
20.
(1)
当l与x轴垂直时,l的方程为x=2,可得点M的坐标为(2,2)或(2,-2),所以直线BM的方程为y=x+1或y=-x-1.
(2)
当l与x轴垂直时,AB为MN的垂直平分线,
所以∠ABM=∠ABN.
当l与x轴不垂直时,设l的方程为y=k(x-2)(k≠0),M(x1,y1),N(x2,y2),
则x1>0,x2>0.
由得ky2-2y-4k=0,则y1+y2=,y1y2=-4.
直线BM,BN的斜率之和为
kBM+kBN=+=,①
将x1=+2,x2=+2及y1+y2=,y1y2=-4代入①式分子,
可得x2y1+x1y2+2(y1+y2)===0,
所以kBM+kBN=0,可知BM,BN的倾斜角互补,
所以∠ABM=∠ABN.
综上,∠ABM=∠ABN.
21.
(1)
f(x)的定义域为(0,+∞),f′(x)=aex-.
由题设知,f′(2)=0,所以a=,
从而f(x)=ex-lnx-1,f′(x)=ex-.
当0
所以f(x)的单调减区间为(0,2),单调增区间为(2,+∞).
(2)
当a≥时,f(x)≥-lnx-1.
设g(x)=-lnx-1,则g′(x)=-.
当0
所以x=1是g(x)的最小值点.
故当x>0时,g(x)≥g(1)=0.
因此,当a≥时,f(x)≥0.
22.
(1)
由x=ρcosθ,x2+y2=ρ2,得C2的直角坐标方程为x2+y2+2x-3=0,即(x+1)2+y2=4.
(2)
由(1)知C2是圆心为A(-1,0),半径为2的圆.
由题设知,C1是过点B(0,2)且关于y轴对称的两条射线.记y轴右边的射线为l1,y轴左边的射线为l2.由于B在圆C2的外面,故C1与C2有且仅有三个公共点等价于l1与C2只有一个公共点且l2与C2有两个公共点,或l2与C2只有一个公共点且l1与C2有两个公共点.
当l1与C2只有一个公共点时,点A到l1所在直线的距离为2,所以=2,故k=-或k=0.经检验,当k=0时,l1与C2没有公共点;当k=-时,l1与C2只有一个公共点,l2与C2有两个公共点.
当l2与C2只有一个公共点时,点A到l2所在直线的距离为2,
所以=2,故k=0或k=.
经检验,当k=0时,l1与C2没有公共点;当k=时,l2与C2没有公共点.
综上,所求C1的方程为y=-|x|+2.
23.
(1)
当a=1时,f(x)=|x+1|-|x-1|,
即f(x)=解得x>.
故不等式f(x)>1的解为.
(2)
当x∈(0,1)时|x+1|-|ax-1|>x成立等价于当x∈(0,1)时|ax-1|<1成立.
若a≤0,则当x∈(0,1)时|ax-1|≥1;
若a>0,|ax-1|<1的解为0
同课章节目录
