第二单元第5课时《四边形分类》练习
图片预览


文档简介
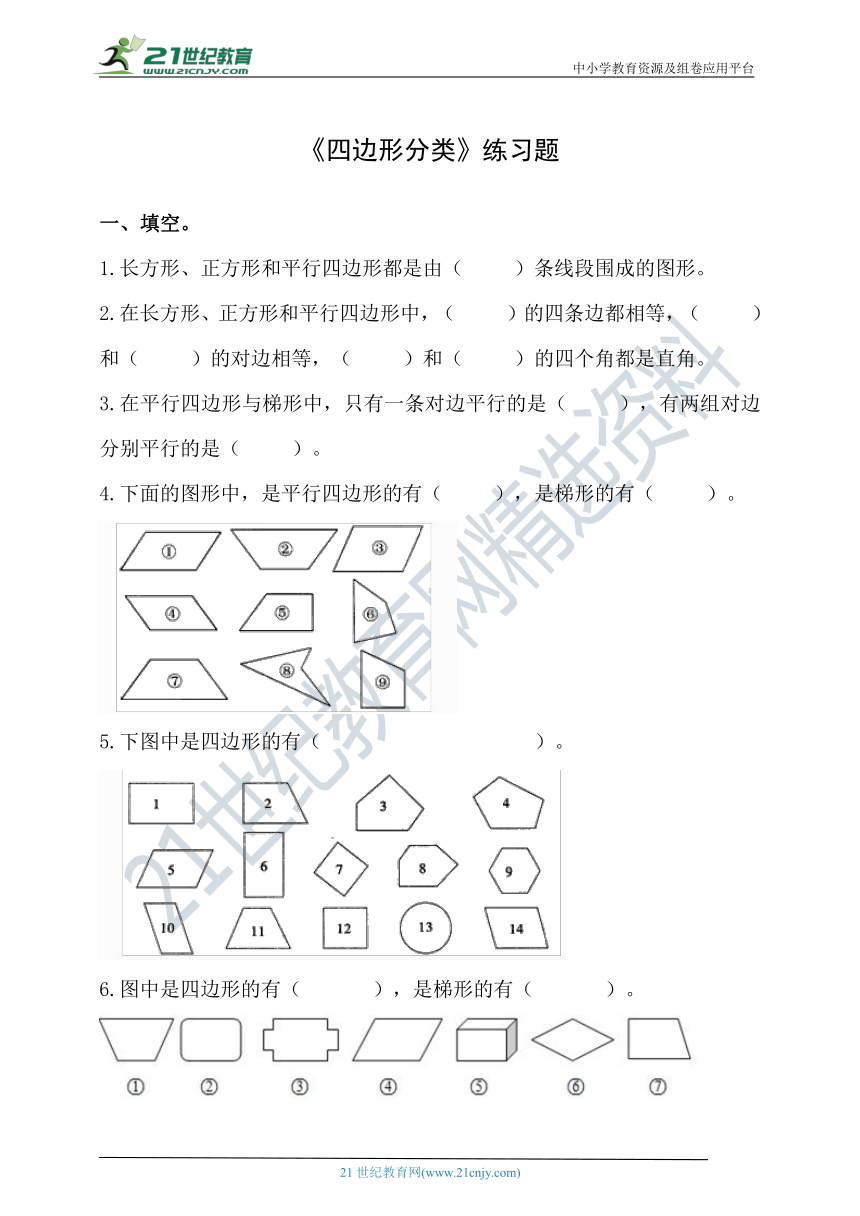
《四边形分类》练习题
一、填空。
1.长方形、正方形和平行四边形都是由( )条线段围成的图形。
2.在长方形、正方形和平行四边形中,( )的四条边都相等,( )和( )的对边相等,( )和( )的四个角都是直角。
3.在平行四边形与梯形中,只有一条对边平行的是( ),有两组对边分别平行的是( )。
4.下面的图形中,是平行四边形的有( ),是梯形的有( )。
5.下图中是四边形的有( )。
6.图中是四边形的有( ),是梯形的有( )。
二、判断。
1.平行四边形是特殊的梯形。 ( )
2.平行四边形的对边相等。 ( )
3.长方形、正方形和梯形都是特殊的平行四边形。 ( )
选一选。
1.梯形中,( )是平行的。
A.上底和下底 B.上底和腰 C.两条腰
2.( )是特殊的长方形。
A.正方形 B.平行四边形 C.梯形
用画平行线的方法把下面图形分别画成长方形、正方形和平行四边形。
画一个梯形,并表上各部分的名称。
六、按要求画一画。
1.在下面长方形中加一条线段,使它成为两个长方形。
在如图中加一条线段,使它变成一个长方形和一个三角形。
答案与解析
一、1.【解析】由四条线段依次首尾相接围成的封闭图形是四边形,长方形、正方形、平行四边形都是四边形,由此求解。
【答案】四。
2.【解析】长方形和正方形和平行四边形都是四边形,所以具备四边形的特征:都有4条直的边,4个角;其中长方形和正方形具备独有特征:4个角都是直角;长方形是特殊的平行四边形,所以具备平行四边形的特征:对边平行且相等;进而解答即可。
【答案】正方形;长方形;平行四边形;长方形;正方形。
3.【解析】根据平行四边形与梯形的意义直接求解。
【答案】梯形;平行四边形。
4.【解析】根据平行四边形与梯形的意义直接求解。
【答案】①③④;②⑤⑦⑨。
5.【解析】根据四边形的意义直接求解。
【答案】1、2、5、6、7、10、11、12、14。
6.【解析】根据四边形与梯形的意义直接求解。
【答案】①④⑥⑦;①⑦。
二、1.【解析】根据平行四边形的性质,平行四边形的两组对边分别平行且相等,而梯形只有一组对边平行,并且平行的一组对边不相等;或由平行四边形和梯形的意义判断,在同一平面内有两组对边分别平行的四边形叫做平行四边形,梯形是指一组对边平行而另一组对边不平行的四边形。
【答案】×。
2.【解析】根据平行四边形边特征求解,即对边平行且相等。
【答案】√。
3.【解析】根据平行四边形的特征:两组对边平行且相等;则得出:长方形、正方形是特殊的平行四边形,而梯形是只有一组对边平行的四边形,另一组对边不平行;进行解答即可。
【答案】×。
2.【解析】正方形是一组邻边相等长方形,是特殊的长方形。
【答案】A。
四、【解析】把三角板的一条直角边与已知直线重合,用直尺靠紧三角板的另一条直角边,沿直尺移动三角板,使三角板的原来和已知直线重合的直角边和顶点重合,过顶点沿三角板的直角边画直线即可。
【答案】
五、【解析】根据梯形的意义画图,然后根据平行的一组边,长的是下底,短的是上底,不平行的边称为腰求解。
【答案】
六、1.【解析】沿长或宽做平行线即可。
【答案】
2.【解析】过下底的右顶点向对边作垂线,即得到一个长方形和一个三角形。
【答案】
一、填空。
1.长方形、正方形和平行四边形都是由( )条线段围成的图形。
2.在长方形、正方形和平行四边形中,( )的四条边都相等,( )和( )的对边相等,( )和( )的四个角都是直角。
3.在平行四边形与梯形中,只有一条对边平行的是( ),有两组对边分别平行的是( )。
4.下面的图形中,是平行四边形的有( ),是梯形的有( )。
5.下图中是四边形的有( )。
6.图中是四边形的有( ),是梯形的有( )。
二、判断。
1.平行四边形是特殊的梯形。 ( )
2.平行四边形的对边相等。 ( )
3.长方形、正方形和梯形都是特殊的平行四边形。 ( )
选一选。
1.梯形中,( )是平行的。
A.上底和下底 B.上底和腰 C.两条腰
2.( )是特殊的长方形。
A.正方形 B.平行四边形 C.梯形
用画平行线的方法把下面图形分别画成长方形、正方形和平行四边形。
画一个梯形,并表上各部分的名称。
六、按要求画一画。
1.在下面长方形中加一条线段,使它成为两个长方形。
在如图中加一条线段,使它变成一个长方形和一个三角形。
答案与解析
一、1.【解析】由四条线段依次首尾相接围成的封闭图形是四边形,长方形、正方形、平行四边形都是四边形,由此求解。
【答案】四。
2.【解析】长方形和正方形和平行四边形都是四边形,所以具备四边形的特征:都有4条直的边,4个角;其中长方形和正方形具备独有特征:4个角都是直角;长方形是特殊的平行四边形,所以具备平行四边形的特征:对边平行且相等;进而解答即可。
【答案】正方形;长方形;平行四边形;长方形;正方形。
3.【解析】根据平行四边形与梯形的意义直接求解。
【答案】梯形;平行四边形。
4.【解析】根据平行四边形与梯形的意义直接求解。
【答案】①③④;②⑤⑦⑨。
5.【解析】根据四边形的意义直接求解。
【答案】1、2、5、6、7、10、11、12、14。
6.【解析】根据四边形与梯形的意义直接求解。
【答案】①④⑥⑦;①⑦。
二、1.【解析】根据平行四边形的性质,平行四边形的两组对边分别平行且相等,而梯形只有一组对边平行,并且平行的一组对边不相等;或由平行四边形和梯形的意义判断,在同一平面内有两组对边分别平行的四边形叫做平行四边形,梯形是指一组对边平行而另一组对边不平行的四边形。
【答案】×。
2.【解析】根据平行四边形边特征求解,即对边平行且相等。
【答案】√。
3.【解析】根据平行四边形的特征:两组对边平行且相等;则得出:长方形、正方形是特殊的平行四边形,而梯形是只有一组对边平行的四边形,另一组对边不平行;进行解答即可。
【答案】×。
2.【解析】正方形是一组邻边相等长方形,是特殊的长方形。
【答案】A。
四、【解析】把三角板的一条直角边与已知直线重合,用直尺靠紧三角板的另一条直角边,沿直尺移动三角板,使三角板的原来和已知直线重合的直角边和顶点重合,过顶点沿三角板的直角边画直线即可。
【答案】
五、【解析】根据梯形的意义画图,然后根据平行的一组边,长的是下底,短的是上底,不平行的边称为腰求解。
【答案】
六、1.【解析】沿长或宽做平行线即可。
【答案】
2.【解析】过下底的右顶点向对边作垂线,即得到一个长方形和一个三角形。
【答案】
