2019年通用版高考数学(理)二轮复习重点增分提优专题2 基本初等函数、函数与方程 Word版含解析
文档属性
| 名称 | 2019年通用版高考数学(理)二轮复习重点增分提优专题2 基本初等函数、函数与方程 Word版含解析 |  | |
| 格式 | zip | ||
| 文件大小 | 502.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-05-06 16:10:53 | ||
图片预览




文档简介
重点增分提优专题二 基本初等函数、函数与方程
[全国卷3年考情分析]
年份 全国卷Ⅰ 全国卷Ⅱ 全国卷Ⅲ
2018 分段函数的零点问题·T9 对数式的比较大小问题·T12
2017 指数与对数的互化、对数运算、比较大小·T11 函数的零点问题·T11
2016 利用幂函数、指数函数、对数函数的单调性比较大小·T8 利用指数函数与幂函数的单调性比较大小·T6
(1)基本初等函数作为高考的命题热点,多考查指数式与对数式的运算、利用函数的性质比较大小,一般出现在第5~12题的位置,有时难度较大.
(2)函数的应用问题多体现在函数零点与方程根的综合问题上,题目可能较难,应引起重视.
[析母题]
[典例] (1)若当x∈R时,函数f(x)=a|x|(a>0,且a≠1)满足f(x)≤1,则函数y=loga(x+1)的图象大致为( )
(2)已知函数f(x)是定义在R上的偶函数,且当x∈[0,+∞)时,函数f(x)是单调递减函数,则f(log25),f,f(log53)的大小关系是( )
A.fB.fC.f(log53)D.f(log25)[解析] (1)由a|x|≤1(x∈R),知0(2)因为f(x)在R上为偶函数,
所以f=f(-log35)=f(log35).
由对数函数的单调性可知,log25>log35>1>log53>0.
又因为f(x)在[0,+∞)上为单调递减函数,
所以f(log53)>f(log35)>f(log25),
即f(log53)>f>f(log25).
[答案] (1)C (2)D
[练子题]
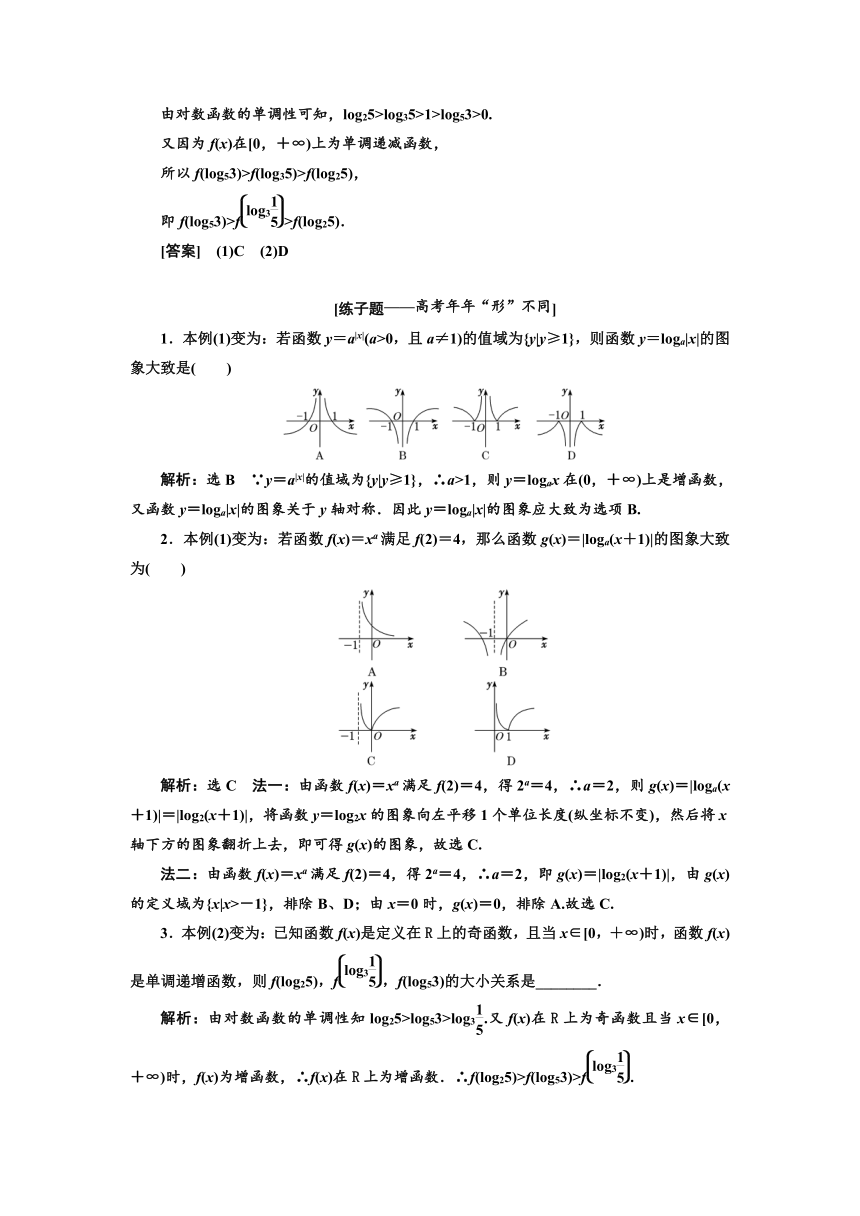
1.本例(1)变为:若函数y=a|x|(a>0,且a≠1)的值域为{y|y≥1},则函数y=loga|x|的图象大致是( )
解析:选B ∵y=a|x|的值域为{y|y≥1},∴a>1,则y=logax在(0,+∞)上是增函数,又函数y=loga|x|的图象关于y轴对称.因此y=loga|x|的图象应大致为选项B.
2.本例(1)变为:若函数f(x)=xa满足f(2)=4,那么函数g(x)=|loga(x+1)|的图象大致为( )
解析:选C 法一:由函数f(x)=xa满足f(2)=4,得2a=4,∴a=2,则g(x)=|loga(x+1)|=|log2(x+1)|,将函数y=log2x的图象向左平移1个单位长度(纵坐标不变),然后将x轴下方的图象翻折上去,即可得g(x)的图象,故选C.
法二:由函数f(x)=xa满足f(2)=4,得2a=4,∴a=2,即g(x)=|log2(x+1)|,由g(x)的定义域为{x|x>-1},排除B、D;由x=0时,g(x)=0,排除A.故选C.
3.本例(2)变为:已知函数f(x)是定义在R上的奇函数,且当x∈[0,+∞)时,函数f(x)是单调递增函数,则f(log25),f,f(log53)的大小关系是________.
解析:由对数函数的单调性知log25>log53>log3.又f(x)在R上为奇函数且当x∈[0, +∞)时,f(x)为增函数,∴f(x)在R上为增函数.∴f(log25)>f(log53)>f.
答案:f(log25)>f(log53)>f
4.本例(2)变为:设f(x)是定义在实数集R上的函数,满足条件y=f(x+1)是偶函数,且当x≥1时,f(x)=x-1,则f,f,f的大小关系是( )
A.f>f>f B.f>f>f
C.f>f>f D.f>f>f
解析:选D 因为函数y=f(x+1)是偶函数,所以f(-x+1)=f(x+1),即函数f(x)的图象关于直线x=1对称,所以f=f,f=f.当x≥1时,f(x)=x-1单调递减,由<<,可得f[解题方略]
基本初等函数的图象与性质的应用技巧
(1)对数函数与指数函数的单调性都取决于其底数的取值,若底数a的值不确定,要注意分a>1和01时,两函数在定义域内都为增函数;当0(2)由指数函数、对数函数与其他函数复合而成的函数,其性质的研究往往通过换元法转化为两个基本初等函数的有关性质,然后根据复合函数的性质与相关函数的性质之间的关系进行判断.
(3)对于幂函数y=xα的性质要注意α>0和α<0两种情况的不同.
[多练强化]
1.(2018·全国卷Ⅲ)设a=log0.20.3,b=log20.3,则( )
A.a+bC.a+b<0解析:选B ∵a=log0.20.3>log0.21=0,b=log20.3∴ab<0.∵=+=log0.30.2+log0.32=log0.30.4,
∴1=log0.30.3>log0.30.4>log0.31=0,
∴0<<1,∴ab2.若函数y=(a>0,a≠1)的定义域和值域都是[0,1],则loga+loga=( )
A.1 B.2
C.3 D.4
解析:选C ∵当a>1时,函数y=在[0,1]上单调递减,∴=1且=0,解得a=2;当03.已知函数f(x)=eq \b\lc\{\rc\ (\a\vs4\al\co1(3-x-1,x≤0,,x,x>0))在区间[-1,m]上的最大值是2,则m的取值范围是________.
解析:f(x)=eq \b\lc\{\rc\ (\a\vs4\al\co1(3-x-1,x≤0,,x,x>0))作出函数的图象,如图所示,因为函数f(x)在[-1,m]上的最大值为2,又f(-1)=f(4)=2,所以-1
答案:(-1,4]
增分考点·广度拓展
?题型一 确定函数零点个数或所在区间
[例1] (1)(2018·邯郸月考)设f(x)=ln x+x-2,则函数f(x)的零点所在的区间为( )
A.(0,1) B.(1,2)
C.(2,3) D.(3,4)
(2)(2018·全国卷Ⅲ)函数f(x)=cos在[0,π]的零点个数为________.
[解析] (1)法一:因为f(1)=0+1-2=-1<0,f(2)=ln 2+2-2=ln 2>0,所以函数f(x)的零点所在区间为(1,2),故选B.
法二:函数f(x)的零点所在的区间可转化为函数g(x)=ln x,h(x)=-x+2图象交点的横坐标所在的取值范围.作出图象如图所示.
由图可知f(x)的零点所在的区间为(1,2).
(2)由题意可知,当3x+=kπ+(k∈Z)时,
f(x)=0.∵x∈[0,π],∴3x+∈,
∴当3x+取值为,,时,f(x)=0,
即函数f(x)=cos在[0,π]的零点个数为3.
[答案] (1)B (2)3
[解题方略]
1.判断函数在某个区间上是否存在零点的方法
(1)解方程:当函数对应的方程易求解时,可通过解方程判断方程是否有根落在给定区间上;
(2)利用零点存在性定理进行判断;
(3)画出函数图象,通过观察图象与x轴在给定区间上是否有交点来判断.
2.判断函数零点个数的3种方法
?题型二 根据函数的零点求参数的范围
[例2] (1)(2018·全国卷Ⅰ)已知函数f(x)=g(x)=f(x)+x+a.若g(x)存在2个零点,则a的取值范围是( )
A.[-1,0) B.[0,+∞)
C.[-1,+∞) D.[1,+∞)
(2)已知定义域为R的偶函数f(x)满足:对?x∈R,有f(x+2)=f(x)-f(1),且当x∈[2,3]时,f(x)=-2x2+12x-18.若函数y=f(x)-loga(x+1)在(0,+∞)上至少有三个零点,则实数a的取值范围为( )
A. B.
C. D.
[解析] (1)令h(x)=-x-a,则g(x)=f(x)-h(x).在同一坐标系中画出y=f(x),y=h(x)的示意图,如图所示.若g(x)存在2个零点,则y=f(x)的图象与y=h(x)的图象有2个交点,平移y=h(x)的图象,可知当直线y=-x-a过点(0,1)时,有2个交点,此时1=-0-a,a=-1.当y=
-x-a在y=-x+1上方,即a<-1时,仅有1个交点,不符合题意.当y=-x-a在y=-x+1下方,即a>-1时,有2个交点,符合题意.综上,a的取值范围为[-1,+∞).故选C.
(2)∵f(x+2)=f(x)-f(1),f(x)是偶函数,∴f(1)=0,∴f(x+2)=f(x),即f(x)是周期为2的周期函数,且y=f(x)的图象关于直线x=2对称,作出函数y=f(x)与g(x)=loga(x+1)的图象如图所示,∵两个函数图象在(0,+∞)上至少有三个交点,
∴g(2)=loga3>f(2)=-2,且0[答案] (1)C (2)A
[解题方略]
利用函数零点的情况求参数的范围的3种方法
直观想象——数形结合法在函数零点问题中的应用
[典例] 已知函数f(x)=eq \b\lc\{\rc\ (\a\vs4\al\co1(3x,x≤1,,logx,x>1,))则函数y=f(x)+x-4的零点个数为( )
A.1 B.2
C.3 D.4
[解析] 函数y=f(x)+x-4的零点个数,即函数y=-x+4与y=f(x)的图象的交点的个数.如图所示,函数y=-x+4与y=f(x)的图象有两个交点,故函数y=f(x)+x-4的零点有2个.故选B.
[答案] B
[素养通路]
直观想象是指借助几何直观和空间想象感知事物的形态与变化,利用空间形式特别是图形,理解和解决数学问题的素养.主要包括:借助空间形式认识事物的位置关系、形态变化与运动规律;利用图形描述、分析数学问题,建立形与数的联系,构建数学问题的直观模型,探索解决问题的思路.
本题是函数零点个数问题,基本思路是数形结合,即把函数拆分为两个基本初等函数,这两个函数图象的交点个数即为函数的零点个数,对于不易直接求解的方程的根的个数的讨论,也是通过根据方程构建两个函数,利用两函数图象交点个数得出对应方程根的个数.考查了直观想象这一核心素养.
A组——“12+4”满分练
一、选择题
1.幂函数y=f(x)的图象经过点(3,),则f(x)是( )
A.偶函数,且在(0,+∞)上是增函数
B.偶函数,且在(0,+∞)上是减函数
C.奇函数,且在(0,+∞)上是减函数
D.非奇非偶函数,且在(0,+∞)上是增函数
解析:选D 设幂函数f(x)=xa,则f(3)=3a=,解得a=,则f(x)=x=,是非奇非偶函数,且在(0,+∞)上是增函数.
2.函数y=ax+2-1(a>0,且a≠1)的图象恒过的点是( )
A.(0,0) B.(0,-1)
C.(-2,0) D.(-2,-1)
解析:选C 令x+2=0,得x=-2,所以当x=-2时,y=a0-1=0,所以y=ax+2-1(a>0,且a≠1)的图象恒过点(-2,0).
3.(2019届高三·益阳、湘潭调研)若a=log32,b=lg 0.2,c=20.2,则a,b,c的大小关系为( )
A.cC.a解析:选B 由对数函数的性质可得a=log32∈(0,1),b=lg 0.2<0.由指数函数的性质可得c=20.2>1,∴b4.(2018·福建第一学期高三期末考试)已知函数f(x)=则函数y=f(x)+3x的零点个数是( )
A.0 B.1
C.2 D.3
解析:选C 令f(x)+3x=0,则或解得x=0或x=-1,所以函数y=f(x)+3x的零点个数是2.故选C.
5.已知函数f(x)=log3-a在区间(1,2)内有零点,则实数a的取值范围是( )
A.(-1,-log32) B.(0,log52)
C.(log32,1) D.(1,log34)
解析:选C ∵函数f(x)=log3-a在区间(1,2)内有零点,且f(x)在(1,2)内单调, ∴f(1)·f(2)<0,即(1-a)·(log32-a)<0,解得log326.(2018·贵阳适应性考试)已知奇函数f(x)在R上是减函数,且a=-f,b=f(log39.1),c=f(20.8),则a,b,c的大小关系为( )
A.a>b>c B.c>b>a
C.b>a>c D.c>a>b
解析:选B ∵f(x)是奇函数,∴a=-f=f=f(log310).
又∵log310>log39.1>log39=2>20.8,且f(x)在R上单调递减,
∴f(log310)b>a,故选B.
7.已知函数f(x)=lg是奇函数,且在x=0处有意义,则该函数为( )
A.(-∞,+∞)上的减函数
B.(-∞,+∞)上的增函数
C.(-1,1)上的减函数
D.(-1,1)上的增函数
解析:选D 由题意知,f(0)=lg(2+a)=0,∴a=-1,∴f(x)=lg=lg,令>0,则-18.若函数f(x)与g(x)的图象关于直线y=x对称,函数f(x)=-x,则f(2)+g(4)=( )
A.3 B.4
C.5 D.6
解析:选D 法一:∵函数f(x)与g(x)的图象关于直线y=x对称,
又f(x)=-x=2x,∴g(x)=log2x,
∴f(2)+g(4)=22+log24=6.
法二:∵f(x)=-x,∴f(2)=4,即函数f(x)的图象经过点(2,4),
∵函数f(x)与g(x)的图象关于直线y=x对称,
∴函数g(x)的图象经过点(4,2),∴f(2)+g(4)=4+2=6.
9.设函数f(x)=ax-k-1(a>0,且a≠1)过定点(2,0),且f(x)在定义域R上是减函数,则g(x)=loga(x+k)的图象是( )
解析:选A 由题意可知a2-k-1=0,解得k=2,所以f(x)=ax-2-1,又f(x)在定义域R上是减函数,所以010.已知函数f(x)=loga(2x2+x)(a>0,且a≠1),当x∈时,恒有f(x)>0,则f(x)的单调递增区间是( )
A. B.(0,+∞)
C. D.
解析:选A 当x∈时,2x2+x∈(0,1),因为当x∈时,恒有f(x)>0,所以00得x>0或x<-.又2x2+x=22-,由复合函数的单调性可知,函数f(x)的单调递增区间为.
11.设方程10x=|lg(-x)|的两根分别为x1,x2,则( )
A.x1x2<0 B.x1x2=1
C.x1x2>1 D.0解析:选D 作出函数y=10x,y=|lg(-x)|的图象,由图象可知,两个根一个小于-1,一个在(-1,0)之间,
不妨设x1<-1,-1则10x1=lg(-x1),
10x2=|lg(-x2)|=-lg(-x2).
两式相减得:
lg(-x1)-(-lg(-x2))=lg(-x1)+lg(-x2)
=lg(x1x2)=10x1-10x2<0,即0
12.(2018·陕西质检)已知定义在R上的函数y=f(x)对任意的x都满足f(x+1)=-f(x),且当0≤x<1时,f(x)=x,则函数g(x)=f(x)-ln|x|的零点个数为( )
A.2 B.3
C.4 D.5
解析:选B 依题意,可知函数g(x)=f(x)-ln|x|的零点个数即为函数y=f(x)的图象与函数y=ln|x|的图象的交点个数.
设-1≤x<0,则0≤x+1<1,
此时有f(x)=-f(x+1)=-(x+1),
又由f(x+1)=-f(x),
得f(x+2)=-f(x+1)=f(x),
即函数f(x)以2为周期的周期函数.
而y=ln|x|=在同一坐标系中作出函数y=f(x)的图象与y=ln|x|的图象如图所示,
由图可知,两图象有3个交点,
即函数g(x)=f(x)-ln|x|有3个零点,故选B.
二、填空题
13.(2018·全国卷Ⅰ)已知函数f(x)=log2(x2+a).若f(3)=1,则a=________.
解析:∵f(x)=log2(x2+a)且f(3)=1,
∴1=log2(9+a),∴9+a=2,∴a=-7.
答案:-7
14.(2019届高三·南宁二中、柳州高中联考)已知函数f(x)=eq \b\lc\{\rc\ (\a\vs4\al\co1(\b\lc\(\rc\)(\a\vs4\al\co1(\f(1,2)))x,x≤0,,logx,x>0,))则f+f=________.
解析:由题可得f=log=2,因为log2<0,所以f=log2=2log26=6,故f+f=8.
答案:8
15.有四个函数:①y=x;②y=21-x;③y=ln(x+1);④y=|1-x|.其中在区间(0,1)内单调递减的函数的序号是________.
解析:分析题意可知①③显然不满足题意,画出②④中的函数图象(图略),易知②④中的函数满足在(0,1)内单调递减.
答案:②④
16.若函数f(x)=有两个不同的零点,则实数a的取值范围是________.
解析:当x>0时,由f(x)=ln x=0,
得x=1.
因为函数f(x)有两个不同的零点,
所以当x≤0时,函数f(x)=2x-a有一个零点,
令f(x)=0,得a=2x,
因为0<2x≤20=1,所以0答案:(0,1]
B组——“12+4”提速练
一、选择题
1.(2017·全国卷Ⅱ)函数f(x)=ln(x2-2x-8)的单调递增区间是( )
A.(-∞,-2) B.(-∞,1)
C.(1,+∞) D.(4,+∞)
解析:选D 由x2-2x-8>0,得x>4或x<-2.因此,函数f(x)=ln(x2-2x-8)的定义域是(-∞,-2)∪(4,+∞).注意到函数y=x2-2x-8在(4,+∞)上单调递增,由复合函数的单调性知,f(x)=ln(x2-2x-8)的单调递增区间是(4,+∞).
2.(2018·福州质检)若函数f(x)的图象向右平移1个单位长度,所得图象与曲线y=ex关于y轴对称,则f(x)的解析式为( )
A.f(x)=ex+1 B.f(x)=ex-1
C.f(x)=e-x+1 D.f(x)=e-x-1
解析:选D 与y=ex的图象关于y轴对称的图象对应的函数为y=e-x.依题意,f(x)的图象向右平移1个单位长度,得y=e-x的图象,∴f(x)的图象是由y=e-x的图象向左平移1个单位长度得到的,∴f(x)=e-(x+1)=e-x-1.
3.函数f(x)=|log2x|+x-2的零点个数为( )
A.1 B.2
C.3 D.4
解析:选B 函数f(x)=|log2x|+x-2的零点个数,就是方程|log2x|+x-2=0的根的个数.
令h(x)=|log2x|,g(x)=2-x,在同一坐标平面上画出两函数的图象,如图所示.
由图象得h(x)与g(x)有2个交点,∴方程|log2x|+x-2=0的根的个数为2.
4.(2018·新疆自治区适应性检测)已知定义在R上的函数f(x)=x,记a=f(0.90.9),b=f(ln(lg 9)),c=f,则a,b,c的大小关系为( )
A.bC.c解析:选C ∵0=lg 11.又0<0.90.9<0.90=1,且函数f(x)=x在R上单调递减,∴c5.(2019届高三·贵阳摸底考试)20世纪30年代,为了防范地震带来的灾害,里克特(C.F.Richter)制定了一种表明地震能量大小的尺度,就是使用测震仪衡量地震能量的等级,地震能量越大,测震仪记录的地震曲线的振幅就越大,这就是我们常说的里氏震级M,其计算公式为M=lg A-lg A0,其中A是被测地震的最大振幅,A0是“标准地震”的振幅.已知5级地震给人的震感已经比较明显,则7级地震的最大振幅是5级地震的最大振幅的多少倍?( )
A.10倍 B.20倍
C.50倍 D.100倍
解析:选D 根据题意有lg A=lg A0+lg 10M=lg(A0·10M),所以A=A0·10M,
则=100.故选D.
6.已知函数f(x)=ax+x-b的零点x0∈(n,n+1)(n∈Z),其中常数a,b满足0A.2 B.1
C.-2 D.-1
解析:选D 由题意得函数f(x)=ax+x-b为增函数,
所以f(-1)=-1-b<0,f(0)=1-b>0,
所以函数f(x)=ax+x-b在(-1,0)内有一个零点,
故n=-1.
7.两个函数的图象经过平移后能够重合,称这两个函数为“同根函数”,给出四个函数:f1(x)=2log2(x+1),f2(x)=log2(x+2),f3(x)=log2x2,f4(x)=log2(2x),则“同根函数”是( )
A.f2(x)与f4(x) B.f1(x)与f3(x)
C.f1(x)与f4(x) D.f3(x)与f4(x)
解析:选A f4(x)=log2(2x)=1+log2x,f2(x)=log2(x+2),将f2(x)的图象沿着x轴先向右平移2个单位得到y=log2x的图象,然后再沿着y轴向上平移1个单位可得到f4(x)的图象,根据“同根函数”的定义可知选A.
8.已知f(x)=|ln(x+1)|,若f(a)=f(b)(aA.a+b>0 B.a+b>1
C.2a+b>0 D.2a+b>1
解析:选A 作出函数f(x)=|ln(x+1)|的图象如图所示,由f(a)=f(b)(a0,又易知-10,∴a+b+4>0,∴a+b>0.故选A.
9.已知定义在R上的函数f(x)满足:①图象关于点(1,0)对称;②f(-1+x)=f(-1-x);③当x∈[-1,1]时,f(x)=则函数y=f(x)-|x|在区间[-3,3]上的零点个数为( )
A.5 B.6
C.7 D.8
解析:选A 因为f(-1+x)=f(-1-x),所以函数f(x)的图象关于直线x=-1对称,又函数f(x)的图象关于点(1,0)对称,如图所示,画出y=f(x)以及g(x)=|x|在[-3,3]上的图象,由图可知,两函数图象的交点个数为5,所以函数y=f(x)-|x|在区间[-3,3]上的零点个数为5,故选A.
10.设函数f(x)=e|ln x|(e为自然对数的底数).若x1≠x2且f(x1)=f(x2),则下列结论一定不成立的是( )
A.x2f(x1)>1 B.x2f(x1)=1
C.x2f(x1)<1 D.x2f(x1)解析:选C f(x)=作出y=f(x)的图象
如图所示,若01,f(x2)=x2>1,x2f(x1)>1,则A成立.若01,f(x1)=x1>1,则x2f(x1)=x2x1=1,则B成立.对于D,若01,x1f(x2)=1,则D不成立;若01,则D成立.故选C.
11.(2018·惠州调研)函数f(x)是定义在R上的奇函数,当x>0时,f(x)=则函数g(x)=xf(x)-1在[-6,+∞)上的所有零点之和为( )
A.8 B.32
C. D.0
解析:选A 令g(x)=xf(x)-1=0,则x≠0,所以函数g(x)的零点之和等价于函数y=f(x)的图象和y=的图象的交点的横坐标之和,分别作出x>0时,y=f(x)和y=的大致图象,如图所示,
由于y=f(x)和y=的图象都关于原点对称,因此函数g(x)在[-6,6]上的所有零点之和为0,而当x=8时,f(x)=,即两函数的图象刚好有1个交点,且当x∈(8,+∞)时,y=的图象都在y=f(x)的图象的上方,因此g(x)在[-6,+∞)上的所有零点之和为8.
12.已知在区间(0,2]上的函数f(x)=且g(x)=f(x)-mx在区间(0,2]内有且仅有两个不同的零点,则实数m的取值范围是( )
A.∪ B.∪
C.∪ D.∪
解析:选A 由函数g(x)=f(x)-mx在(0,2]内有且仅有两个不同的零点,得y=f(x),y=mx在(0,2]内的图象有且仅有两个不同的交点.当y=mx与y=-3在(0,1]内相切时,mx2+3x-1=0,Δ=9+4m=0,m=-,结合图象可得当-二、填空题
13.(2019届高三·湖北八校联考)已知函数f(x)=若f(e2)=f(1),f(e)=f(0),则函数f(x)的值域为________.
解析:由题意可得解得
则当x>0时,f(x)=(ln x)2-2ln x+3=(ln x-1)2+2≥2;
当x≤0时,则函数f(x)的值域为∪[2,+∞).
答案:∪[2,+∞)
14.已知在(0,+∞)上函数f(x)=则不等式log2x-(log4x-1)·f(log3x+1)≤5的解集为________.
解析:原不等式等价于eq \b\lc\{\rc\ (\a\vs4\al\co1(log3x+1≥1,,log2x-\b\lc\(\rc\)(\a\vs4\al\co1(log4x-1))≤5))
或eq \b\lc\{\rc\ (\a\vs4\al\co1(0<log3x+1<1,,log2x+2\b\lc\(\rc\)(\a\vs4\al\co1(log4x-1))≤5,))
解得1≤x≤4或<x<1,
所以原不等式的解集为.
答案:
15.已知幂函数f(x)=(m-1)2x在(0,+∞)上单调递增,函数g(x)=2x-k,当x∈[1,2)时,记f(x),g(x)的值域分别为集合A,B,若A∪B=A,则实数k的取值范围是________.
解析:∵f(x)是幂函数,
∴(m-1)2=1,解得m=2或m=0.
若m=2,则f(x)=x-2,f(x)在(0,+∞)上单调递减,不满足条件;
若m=0,则f(x)=x2,f(x)在(0,+∞)上单调递增,满足条件,
故f(x)=x2.
当x∈[1,2)时,f(x)∈[1,4),g(x)∈[2-k,4-k),
即A=[1,4),B=[2-k,4-k),
∵A∪B=A,∴B?A,
则解得0≤k≤1.
答案:[0,1]
16.若关于x的方程(lg a+lg x)·(lg a+2lg x)=4的所有解都大于1,则实数a的取值范围为________.
解析:由题意可得2(lg x)2+3(lg a)·(lg x)+(lg a)2-4=0,令lg x=t>0,
则有2t2+3(lg a)·t+(lg a)2-4=0的解都是正数,
设f(t)=2t2+3(lg a)·t+(lg a)2-4,
则
解得lg a<-2,
所以0答案:
[全国卷3年考情分析]
年份 全国卷Ⅰ 全国卷Ⅱ 全国卷Ⅲ
2018 分段函数的零点问题·T9 对数式的比较大小问题·T12
2017 指数与对数的互化、对数运算、比较大小·T11 函数的零点问题·T11
2016 利用幂函数、指数函数、对数函数的单调性比较大小·T8 利用指数函数与幂函数的单调性比较大小·T6
(1)基本初等函数作为高考的命题热点,多考查指数式与对数式的运算、利用函数的性质比较大小,一般出现在第5~12题的位置,有时难度较大.
(2)函数的应用问题多体现在函数零点与方程根的综合问题上,题目可能较难,应引起重视.
[析母题]
[典例] (1)若当x∈R时,函数f(x)=a|x|(a>0,且a≠1)满足f(x)≤1,则函数y=loga(x+1)的图象大致为( )
(2)已知函数f(x)是定义在R上的偶函数,且当x∈[0,+∞)时,函数f(x)是单调递减函数,则f(log25),f,f(log53)的大小关系是( )
A.f
所以f=f(-log35)=f(log35).
由对数函数的单调性可知,log25>log35>1>log53>0.
又因为f(x)在[0,+∞)上为单调递减函数,
所以f(log53)>f(log35)>f(log25),
即f(log53)>f>f(log25).
[答案] (1)C (2)D
[练子题]
1.本例(1)变为:若函数y=a|x|(a>0,且a≠1)的值域为{y|y≥1},则函数y=loga|x|的图象大致是( )
解析:选B ∵y=a|x|的值域为{y|y≥1},∴a>1,则y=logax在(0,+∞)上是增函数,又函数y=loga|x|的图象关于y轴对称.因此y=loga|x|的图象应大致为选项B.
2.本例(1)变为:若函数f(x)=xa满足f(2)=4,那么函数g(x)=|loga(x+1)|的图象大致为( )
解析:选C 法一:由函数f(x)=xa满足f(2)=4,得2a=4,∴a=2,则g(x)=|loga(x+1)|=|log2(x+1)|,将函数y=log2x的图象向左平移1个单位长度(纵坐标不变),然后将x轴下方的图象翻折上去,即可得g(x)的图象,故选C.
法二:由函数f(x)=xa满足f(2)=4,得2a=4,∴a=2,即g(x)=|log2(x+1)|,由g(x)的定义域为{x|x>-1},排除B、D;由x=0时,g(x)=0,排除A.故选C.
3.本例(2)变为:已知函数f(x)是定义在R上的奇函数,且当x∈[0,+∞)时,函数f(x)是单调递增函数,则f(log25),f,f(log53)的大小关系是________.
解析:由对数函数的单调性知log25>log53>log3.又f(x)在R上为奇函数且当x∈[0, +∞)时,f(x)为增函数,∴f(x)在R上为增函数.∴f(log25)>f(log53)>f.
答案:f(log25)>f(log53)>f
4.本例(2)变为:设f(x)是定义在实数集R上的函数,满足条件y=f(x+1)是偶函数,且当x≥1时,f(x)=x-1,则f,f,f的大小关系是( )
A.f>f>f B.f>f>f
C.f>f>f D.f>f>f
解析:选D 因为函数y=f(x+1)是偶函数,所以f(-x+1)=f(x+1),即函数f(x)的图象关于直线x=1对称,所以f=f,f=f.当x≥1时,f(x)=x-1单调递减,由<<,可得f
基本初等函数的图象与性质的应用技巧
(1)对数函数与指数函数的单调性都取决于其底数的取值,若底数a的值不确定,要注意分a>1和0
(3)对于幂函数y=xα的性质要注意α>0和α<0两种情况的不同.
[多练强化]
1.(2018·全国卷Ⅲ)设a=log0.20.3,b=log20.3,则( )
A.a+b
∴1=log0.30.3>log0.30.4>log0.31=0,
∴0<<1,∴ab
A.1 B.2
C.3 D.4
解析:选C ∵当a>1时,函数y=在[0,1]上单调递减,∴=1且=0,解得a=2;当0
解析:f(x)=eq \b\lc\{\rc\ (\a\vs4\al\co1(3-x-1,x≤0,,x,x>0))作出函数的图象,如图所示,因为函数f(x)在[-1,m]上的最大值为2,又f(-1)=f(4)=2,所以-1
答案:(-1,4]
增分考点·广度拓展
?题型一 确定函数零点个数或所在区间
[例1] (1)(2018·邯郸月考)设f(x)=ln x+x-2,则函数f(x)的零点所在的区间为( )
A.(0,1) B.(1,2)
C.(2,3) D.(3,4)
(2)(2018·全国卷Ⅲ)函数f(x)=cos在[0,π]的零点个数为________.
[解析] (1)法一:因为f(1)=0+1-2=-1<0,f(2)=ln 2+2-2=ln 2>0,所以函数f(x)的零点所在区间为(1,2),故选B.
法二:函数f(x)的零点所在的区间可转化为函数g(x)=ln x,h(x)=-x+2图象交点的横坐标所在的取值范围.作出图象如图所示.
由图可知f(x)的零点所在的区间为(1,2).
(2)由题意可知,当3x+=kπ+(k∈Z)时,
f(x)=0.∵x∈[0,π],∴3x+∈,
∴当3x+取值为,,时,f(x)=0,
即函数f(x)=cos在[0,π]的零点个数为3.
[答案] (1)B (2)3
[解题方略]
1.判断函数在某个区间上是否存在零点的方法
(1)解方程:当函数对应的方程易求解时,可通过解方程判断方程是否有根落在给定区间上;
(2)利用零点存在性定理进行判断;
(3)画出函数图象,通过观察图象与x轴在给定区间上是否有交点来判断.
2.判断函数零点个数的3种方法
?题型二 根据函数的零点求参数的范围
[例2] (1)(2018·全国卷Ⅰ)已知函数f(x)=g(x)=f(x)+x+a.若g(x)存在2个零点,则a的取值范围是( )
A.[-1,0) B.[0,+∞)
C.[-1,+∞) D.[1,+∞)
(2)已知定义域为R的偶函数f(x)满足:对?x∈R,有f(x+2)=f(x)-f(1),且当x∈[2,3]时,f(x)=-2x2+12x-18.若函数y=f(x)-loga(x+1)在(0,+∞)上至少有三个零点,则实数a的取值范围为( )
A. B.
C. D.
[解析] (1)令h(x)=-x-a,则g(x)=f(x)-h(x).在同一坐标系中画出y=f(x),y=h(x)的示意图,如图所示.若g(x)存在2个零点,则y=f(x)的图象与y=h(x)的图象有2个交点,平移y=h(x)的图象,可知当直线y=-x-a过点(0,1)时,有2个交点,此时1=-0-a,a=-1.当y=
-x-a在y=-x+1上方,即a<-1时,仅有1个交点,不符合题意.当y=-x-a在y=-x+1下方,即a>-1时,有2个交点,符合题意.综上,a的取值范围为[-1,+∞).故选C.
(2)∵f(x+2)=f(x)-f(1),f(x)是偶函数,∴f(1)=0,∴f(x+2)=f(x),即f(x)是周期为2的周期函数,且y=f(x)的图象关于直线x=2对称,作出函数y=f(x)与g(x)=loga(x+1)的图象如图所示,∵两个函数图象在(0,+∞)上至少有三个交点,
∴g(2)=loga3>f(2)=-2,且0
[解题方略]
利用函数零点的情况求参数的范围的3种方法
直观想象——数形结合法在函数零点问题中的应用
[典例] 已知函数f(x)=eq \b\lc\{\rc\ (\a\vs4\al\co1(3x,x≤1,,logx,x>1,))则函数y=f(x)+x-4的零点个数为( )
A.1 B.2
C.3 D.4
[解析] 函数y=f(x)+x-4的零点个数,即函数y=-x+4与y=f(x)的图象的交点的个数.如图所示,函数y=-x+4与y=f(x)的图象有两个交点,故函数y=f(x)+x-4的零点有2个.故选B.
[答案] B
[素养通路]
直观想象是指借助几何直观和空间想象感知事物的形态与变化,利用空间形式特别是图形,理解和解决数学问题的素养.主要包括:借助空间形式认识事物的位置关系、形态变化与运动规律;利用图形描述、分析数学问题,建立形与数的联系,构建数学问题的直观模型,探索解决问题的思路.
本题是函数零点个数问题,基本思路是数形结合,即把函数拆分为两个基本初等函数,这两个函数图象的交点个数即为函数的零点个数,对于不易直接求解的方程的根的个数的讨论,也是通过根据方程构建两个函数,利用两函数图象交点个数得出对应方程根的个数.考查了直观想象这一核心素养.
A组——“12+4”满分练
一、选择题
1.幂函数y=f(x)的图象经过点(3,),则f(x)是( )
A.偶函数,且在(0,+∞)上是增函数
B.偶函数,且在(0,+∞)上是减函数
C.奇函数,且在(0,+∞)上是减函数
D.非奇非偶函数,且在(0,+∞)上是增函数
解析:选D 设幂函数f(x)=xa,则f(3)=3a=,解得a=,则f(x)=x=,是非奇非偶函数,且在(0,+∞)上是增函数.
2.函数y=ax+2-1(a>0,且a≠1)的图象恒过的点是( )
A.(0,0) B.(0,-1)
C.(-2,0) D.(-2,-1)
解析:选C 令x+2=0,得x=-2,所以当x=-2时,y=a0-1=0,所以y=ax+2-1(a>0,且a≠1)的图象恒过点(-2,0).
3.(2019届高三·益阳、湘潭调研)若a=log32,b=lg 0.2,c=20.2,则a,b,c的大小关系为( )
A.c
A.0 B.1
C.2 D.3
解析:选C 令f(x)+3x=0,则或解得x=0或x=-1,所以函数y=f(x)+3x的零点个数是2.故选C.
5.已知函数f(x)=log3-a在区间(1,2)内有零点,则实数a的取值范围是( )
A.(-1,-log32) B.(0,log52)
C.(log32,1) D.(1,log34)
解析:选C ∵函数f(x)=log3-a在区间(1,2)内有零点,且f(x)在(1,2)内单调, ∴f(1)·f(2)<0,即(1-a)·(log32-a)<0,解得log32
A.a>b>c B.c>b>a
C.b>a>c D.c>a>b
解析:选B ∵f(x)是奇函数,∴a=-f=f=f(log310).
又∵log310>log39.1>log39=2>20.8,且f(x)在R上单调递减,
∴f(log310)
7.已知函数f(x)=lg是奇函数,且在x=0处有意义,则该函数为( )
A.(-∞,+∞)上的减函数
B.(-∞,+∞)上的增函数
C.(-1,1)上的减函数
D.(-1,1)上的增函数
解析:选D 由题意知,f(0)=lg(2+a)=0,∴a=-1,∴f(x)=lg=lg,令>0,则-1
A.3 B.4
C.5 D.6
解析:选D 法一:∵函数f(x)与g(x)的图象关于直线y=x对称,
又f(x)=-x=2x,∴g(x)=log2x,
∴f(2)+g(4)=22+log24=6.
法二:∵f(x)=-x,∴f(2)=4,即函数f(x)的图象经过点(2,4),
∵函数f(x)与g(x)的图象关于直线y=x对称,
∴函数g(x)的图象经过点(4,2),∴f(2)+g(4)=4+2=6.
9.设函数f(x)=ax-k-1(a>0,且a≠1)过定点(2,0),且f(x)在定义域R上是减函数,则g(x)=loga(x+k)的图象是( )
解析:选A 由题意可知a2-k-1=0,解得k=2,所以f(x)=ax-2-1,又f(x)在定义域R上是减函数,所以0
A. B.(0,+∞)
C. D.
解析:选A 当x∈时,2x2+x∈(0,1),因为当x∈时,恒有f(x)>0,所以0
11.设方程10x=|lg(-x)|的两根分别为x1,x2,则( )
A.x1x2<0 B.x1x2=1
C.x1x2>1 D.0
不妨设x1<-1,-1
10x2=|lg(-x2)|=-lg(-x2).
两式相减得:
lg(-x1)-(-lg(-x2))=lg(-x1)+lg(-x2)
=lg(x1x2)=10x1-10x2<0,即0
12.(2018·陕西质检)已知定义在R上的函数y=f(x)对任意的x都满足f(x+1)=-f(x),且当0≤x<1时,f(x)=x,则函数g(x)=f(x)-ln|x|的零点个数为( )
A.2 B.3
C.4 D.5
解析:选B 依题意,可知函数g(x)=f(x)-ln|x|的零点个数即为函数y=f(x)的图象与函数y=ln|x|的图象的交点个数.
设-1≤x<0,则0≤x+1<1,
此时有f(x)=-f(x+1)=-(x+1),
又由f(x+1)=-f(x),
得f(x+2)=-f(x+1)=f(x),
即函数f(x)以2为周期的周期函数.
而y=ln|x|=在同一坐标系中作出函数y=f(x)的图象与y=ln|x|的图象如图所示,
由图可知,两图象有3个交点,
即函数g(x)=f(x)-ln|x|有3个零点,故选B.
二、填空题
13.(2018·全国卷Ⅰ)已知函数f(x)=log2(x2+a).若f(3)=1,则a=________.
解析:∵f(x)=log2(x2+a)且f(3)=1,
∴1=log2(9+a),∴9+a=2,∴a=-7.
答案:-7
14.(2019届高三·南宁二中、柳州高中联考)已知函数f(x)=eq \b\lc\{\rc\ (\a\vs4\al\co1(\b\lc\(\rc\)(\a\vs4\al\co1(\f(1,2)))x,x≤0,,logx,x>0,))则f+f=________.
解析:由题可得f=log=2,因为log2<0,所以f=log2=2log26=6,故f+f=8.
答案:8
15.有四个函数:①y=x;②y=21-x;③y=ln(x+1);④y=|1-x|.其中在区间(0,1)内单调递减的函数的序号是________.
解析:分析题意可知①③显然不满足题意,画出②④中的函数图象(图略),易知②④中的函数满足在(0,1)内单调递减.
答案:②④
16.若函数f(x)=有两个不同的零点,则实数a的取值范围是________.
解析:当x>0时,由f(x)=ln x=0,
得x=1.
因为函数f(x)有两个不同的零点,
所以当x≤0时,函数f(x)=2x-a有一个零点,
令f(x)=0,得a=2x,
因为0<2x≤20=1,所以0
B组——“12+4”提速练
一、选择题
1.(2017·全国卷Ⅱ)函数f(x)=ln(x2-2x-8)的单调递增区间是( )
A.(-∞,-2) B.(-∞,1)
C.(1,+∞) D.(4,+∞)
解析:选D 由x2-2x-8>0,得x>4或x<-2.因此,函数f(x)=ln(x2-2x-8)的定义域是(-∞,-2)∪(4,+∞).注意到函数y=x2-2x-8在(4,+∞)上单调递增,由复合函数的单调性知,f(x)=ln(x2-2x-8)的单调递增区间是(4,+∞).
2.(2018·福州质检)若函数f(x)的图象向右平移1个单位长度,所得图象与曲线y=ex关于y轴对称,则f(x)的解析式为( )
A.f(x)=ex+1 B.f(x)=ex-1
C.f(x)=e-x+1 D.f(x)=e-x-1
解析:选D 与y=ex的图象关于y轴对称的图象对应的函数为y=e-x.依题意,f(x)的图象向右平移1个单位长度,得y=e-x的图象,∴f(x)的图象是由y=e-x的图象向左平移1个单位长度得到的,∴f(x)=e-(x+1)=e-x-1.
3.函数f(x)=|log2x|+x-2的零点个数为( )
A.1 B.2
C.3 D.4
解析:选B 函数f(x)=|log2x|+x-2的零点个数,就是方程|log2x|+x-2=0的根的个数.
令h(x)=|log2x|,g(x)=2-x,在同一坐标平面上画出两函数的图象,如图所示.
由图象得h(x)与g(x)有2个交点,∴方程|log2x|+x-2=0的根的个数为2.
4.(2018·新疆自治区适应性检测)已知定义在R上的函数f(x)=x,记a=f(0.90.9),b=f(ln(lg 9)),c=f,则a,b,c的大小关系为( )
A.b
A.10倍 B.20倍
C.50倍 D.100倍
解析:选D 根据题意有lg A=lg A0+lg 10M=lg(A0·10M),所以A=A0·10M,
则=100.故选D.
6.已知函数f(x)=ax+x-b的零点x0∈(n,n+1)(n∈Z),其中常数a,b满足0
C.-2 D.-1
解析:选D 由题意得函数f(x)=ax+x-b为增函数,
所以f(-1)=-1-b<0,f(0)=1-b>0,
所以函数f(x)=ax+x-b在(-1,0)内有一个零点,
故n=-1.
7.两个函数的图象经过平移后能够重合,称这两个函数为“同根函数”,给出四个函数:f1(x)=2log2(x+1),f2(x)=log2(x+2),f3(x)=log2x2,f4(x)=log2(2x),则“同根函数”是( )
A.f2(x)与f4(x) B.f1(x)与f3(x)
C.f1(x)与f4(x) D.f3(x)与f4(x)
解析:选A f4(x)=log2(2x)=1+log2x,f2(x)=log2(x+2),将f2(x)的图象沿着x轴先向右平移2个单位得到y=log2x的图象,然后再沿着y轴向上平移1个单位可得到f4(x)的图象,根据“同根函数”的定义可知选A.
8.已知f(x)=|ln(x+1)|,若f(a)=f(b)(a
C.2a+b>0 D.2a+b>1
解析:选A 作出函数f(x)=|ln(x+1)|的图象如图所示,由f(a)=f(b)(a
9.已知定义在R上的函数f(x)满足:①图象关于点(1,0)对称;②f(-1+x)=f(-1-x);③当x∈[-1,1]时,f(x)=则函数y=f(x)-|x|在区间[-3,3]上的零点个数为( )
A.5 B.6
C.7 D.8
解析:选A 因为f(-1+x)=f(-1-x),所以函数f(x)的图象关于直线x=-1对称,又函数f(x)的图象关于点(1,0)对称,如图所示,画出y=f(x)以及g(x)=|x|在[-3,3]上的图象,由图可知,两函数图象的交点个数为5,所以函数y=f(x)-|x|在区间[-3,3]上的零点个数为5,故选A.
10.设函数f(x)=e|ln x|(e为自然对数的底数).若x1≠x2且f(x1)=f(x2),则下列结论一定不成立的是( )
A.x2f(x1)>1 B.x2f(x1)=1
C.x2f(x1)<1 D.x2f(x1)
如图所示,若0
11.(2018·惠州调研)函数f(x)是定义在R上的奇函数,当x>0时,f(x)=则函数g(x)=xf(x)-1在[-6,+∞)上的所有零点之和为( )
A.8 B.32
C. D.0
解析:选A 令g(x)=xf(x)-1=0,则x≠0,所以函数g(x)的零点之和等价于函数y=f(x)的图象和y=的图象的交点的横坐标之和,分别作出x>0时,y=f(x)和y=的大致图象,如图所示,
由于y=f(x)和y=的图象都关于原点对称,因此函数g(x)在[-6,6]上的所有零点之和为0,而当x=8时,f(x)=,即两函数的图象刚好有1个交点,且当x∈(8,+∞)时,y=的图象都在y=f(x)的图象的上方,因此g(x)在[-6,+∞)上的所有零点之和为8.
12.已知在区间(0,2]上的函数f(x)=且g(x)=f(x)-mx在区间(0,2]内有且仅有两个不同的零点,则实数m的取值范围是( )
A.∪ B.∪
C.∪ D.∪
解析:选A 由函数g(x)=f(x)-mx在(0,2]内有且仅有两个不同的零点,得y=f(x),y=mx在(0,2]内的图象有且仅有两个不同的交点.当y=mx与y=-3在(0,1]内相切时,mx2+3x-1=0,Δ=9+4m=0,m=-,结合图象可得当-
13.(2019届高三·湖北八校联考)已知函数f(x)=若f(e2)=f(1),f(e)=f(0),则函数f(x)的值域为________.
解析:由题意可得解得
则当x>0时,f(x)=(ln x)2-2ln x+3=(ln x-1)2+2≥2;
当x≤0时,
答案:∪[2,+∞)
14.已知在(0,+∞)上函数f(x)=则不等式log2x-(log4x-1)·f(log3x+1)≤5的解集为________.
解析:原不等式等价于eq \b\lc\{\rc\ (\a\vs4\al\co1(log3x+1≥1,,log2x-\b\lc\(\rc\)(\a\vs4\al\co1(log4x-1))≤5))
或eq \b\lc\{\rc\ (\a\vs4\al\co1(0<log3x+1<1,,log2x+2\b\lc\(\rc\)(\a\vs4\al\co1(log4x-1))≤5,))
解得1≤x≤4或<x<1,
所以原不等式的解集为.
答案:
15.已知幂函数f(x)=(m-1)2x在(0,+∞)上单调递增,函数g(x)=2x-k,当x∈[1,2)时,记f(x),g(x)的值域分别为集合A,B,若A∪B=A,则实数k的取值范围是________.
解析:∵f(x)是幂函数,
∴(m-1)2=1,解得m=2或m=0.
若m=2,则f(x)=x-2,f(x)在(0,+∞)上单调递减,不满足条件;
若m=0,则f(x)=x2,f(x)在(0,+∞)上单调递增,满足条件,
故f(x)=x2.
当x∈[1,2)时,f(x)∈[1,4),g(x)∈[2-k,4-k),
即A=[1,4),B=[2-k,4-k),
∵A∪B=A,∴B?A,
则解得0≤k≤1.
答案:[0,1]
16.若关于x的方程(lg a+lg x)·(lg a+2lg x)=4的所有解都大于1,则实数a的取值范围为________.
解析:由题意可得2(lg x)2+3(lg a)·(lg x)+(lg a)2-4=0,令lg x=t>0,
则有2t2+3(lg a)·t+(lg a)2-4=0的解都是正数,
设f(t)=2t2+3(lg a)·t+(lg a)2-4,
则
解得lg a<-2,
所以0
同课章节目录
