2019年浙江数学高考真题试卷(Word版,无答案)
文档属性
| 名称 | 2019年浙江数学高考真题试卷(Word版,无答案) | 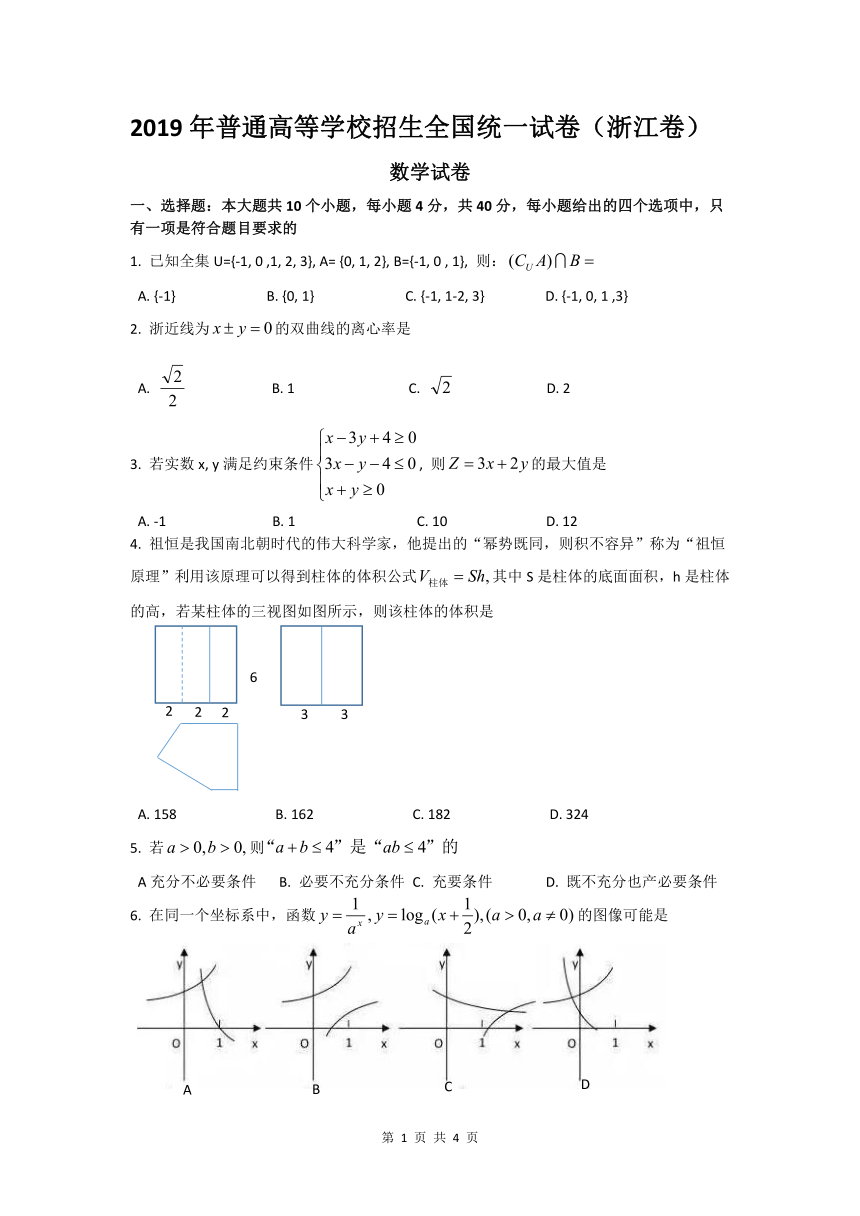 | |
| 格式 | zip | ||
| 文件大小 | 204.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-06-08 20:20:08 | ||
图片预览


文档简介
2019年普通高等学校招生全国统一试卷(浙江卷)
数学试卷
一、选择题:本大题共10个小题,每小题4分,共40分,每小题给出的四个选项中,只有一项是符合题目要求的
已知全集U={-1,
0
,1,
2,
3},
A=
{0,
1,
2},
B={-1,
0
,
1},
则:
A.
{-1}
B.
{0,
1}
C.
{-1,
1-2,
3}
D.
{-1,
0,
1
,3}
浙近线为的双曲线的离心率是
A.
B.
1
C.
D.
2
若实数x,
y满足约束条件,
则的最大值是
A.
-1
B.
1
C.
10
D.
12
祖恒是我国南北朝时代的伟大科学家,他提出的“幂势既同,则积不容异”称为“祖恒原理”利用该原理可以得到柱体的体积公式其中S是柱体的底面面积,h是柱体的高,若某柱体的三视图如图所示,则该柱体的体积是
A.
158
B.
162
C.
182
D.
324
若则
A充分不必要条件
B.
必要不充分条件
C.
充要条件
D.
既不充分也产必要条件
在同一个坐标系中,函数的图像可能是
设0随机变量x的分布列是
x
0
a
1
p
则当a在(0
,
1)内增大时
A.
D(x)增大
B.
D(x)减小
C.
D(x)先增大后冲减小
D.
D(x)减小后增大
设三棱锥V-ABC的底面是正三角形,侧棱长均相等,P是棱VA上的点(不含端点),设直线PB与直线AC所成的角为,
直线PB与平面ABC所成的角为,二面角P-AC-B的平面角为,
则
A.
B.
C.
D.
设,
若函数恰有3个零点,则
A.
a<-1,
b<0
B.
a<-1,
b>0
C.
a>-1,
b<0
D.
a>-1,
b>0
10.
设,则
A.
当
B.
当
C.
当
D.
当
二、填空题:本大题共7个小题,多空题每题6分,单空题每题4分,共36分
复数,则
已知圆C的圆心坐标是(0,
m),
半径是r,若直线2x-y+3=0与圆相切与点A(-2,
-1),则
在二项式的展开式中,常数项是
,系数为有理数的项的个数是
在点D在线段AC上,若则BD=
,cos
已知椭圆的左焦点为F,
点P在椭圆上且在x轴的上方,若线段PF的中点在以原点O为圆心,|OF|为半径的圆上,则直线PF的斜率是
已知,
函数,
若存在使得,
则实数a的最大值是
已知正方形ABCD的边长为1,当每个取遍时,的最小值是
最大值是
三、解答题:本大题共5个小题,共74分,解答普写出文字说明、证明或演算步骤。
(满分14分)
设函数
(1)已知,
函数是偶函数,求的值
(2)求函数的值域。
(满分15分)
如图,已知三棱柱,平面平面ABC,
A1A=A1C=AC,
E,F分别是AC,
A1B1的中点,
(1)证明:EFBC
(2)求直线EF与平面A1BC所成角的余弦值。
(满分15分)
设等差数列的前n项和为S
n
,a
3=4,
a4=S
3
,数列满足:对每个成等比数列
(1)
求数列的通项公式,
(2)
设,证明:
(满分15分)
如图,已知点F(1,
0)为抛物线的焦点,过F点的直线交抛物线于A,
B两点,点C在抛物线上,使得的重心G在x轴上,直线AC交x轴于点Q,
Q点在F点的右侧,设的面积分别为S1
,
S2
.
(1)
求p的值及抛物线的准线方程;
(2)
求的最小值及此时点G的坐标。
(满分15分)
已知实数,
函数
(1)
当时,求函数f(x)的单调区间;
(2)
对任意,都有,
求a的取舍范围。
数学试卷
一、选择题:本大题共10个小题,每小题4分,共40分,每小题给出的四个选项中,只有一项是符合题目要求的
已知全集U={-1,
0
,1,
2,
3},
A=
{0,
1,
2},
B={-1,
0
,
1},
则:
A.
{-1}
B.
{0,
1}
C.
{-1,
1-2,
3}
D.
{-1,
0,
1
,3}
浙近线为的双曲线的离心率是
A.
B.
1
C.
D.
2
若实数x,
y满足约束条件,
则的最大值是
A.
-1
B.
1
C.
10
D.
12
祖恒是我国南北朝时代的伟大科学家,他提出的“幂势既同,则积不容异”称为“祖恒原理”利用该原理可以得到柱体的体积公式其中S是柱体的底面面积,h是柱体的高,若某柱体的三视图如图所示,则该柱体的体积是
A.
158
B.
162
C.
182
D.
324
若则
A充分不必要条件
B.
必要不充分条件
C.
充要条件
D.
既不充分也产必要条件
在同一个坐标系中,函数的图像可能是
设0
x
0
a
1
p
则当a在(0
,
1)内增大时
A.
D(x)增大
B.
D(x)减小
C.
D(x)先增大后冲减小
D.
D(x)减小后增大
设三棱锥V-ABC的底面是正三角形,侧棱长均相等,P是棱VA上的点(不含端点),设直线PB与直线AC所成的角为,
直线PB与平面ABC所成的角为,二面角P-AC-B的平面角为,
则
A.
B.
C.
D.
设,
若函数恰有3个零点,则
A.
a<-1,
b<0
B.
a<-1,
b>0
C.
a>-1,
b<0
D.
a>-1,
b>0
10.
设,则
A.
当
B.
当
C.
当
D.
当
二、填空题:本大题共7个小题,多空题每题6分,单空题每题4分,共36分
复数,则
已知圆C的圆心坐标是(0,
m),
半径是r,若直线2x-y+3=0与圆相切与点A(-2,
-1),则
在二项式的展开式中,常数项是
,系数为有理数的项的个数是
在点D在线段AC上,若则BD=
,cos
已知椭圆的左焦点为F,
点P在椭圆上且在x轴的上方,若线段PF的中点在以原点O为圆心,|OF|为半径的圆上,则直线PF的斜率是
已知,
函数,
若存在使得,
则实数a的最大值是
已知正方形ABCD的边长为1,当每个取遍时,的最小值是
最大值是
三、解答题:本大题共5个小题,共74分,解答普写出文字说明、证明或演算步骤。
(满分14分)
设函数
(1)已知,
函数是偶函数,求的值
(2)求函数的值域。
(满分15分)
如图,已知三棱柱,平面平面ABC,
A1A=A1C=AC,
E,F分别是AC,
A1B1的中点,
(1)证明:EFBC
(2)求直线EF与平面A1BC所成角的余弦值。
(满分15分)
设等差数列的前n项和为S
n
,a
3=4,
a4=S
3
,数列满足:对每个成等比数列
(1)
求数列的通项公式,
(2)
设,证明:
(满分15分)
如图,已知点F(1,
0)为抛物线的焦点,过F点的直线交抛物线于A,
B两点,点C在抛物线上,使得的重心G在x轴上,直线AC交x轴于点Q,
Q点在F点的右侧,设的面积分别为S1
,
S2
.
(1)
求p的值及抛物线的准线方程;
(2)
求的最小值及此时点G的坐标。
(满分15分)
已知实数,
函数
(1)
当时,求函数f(x)的单调区间;
(2)
对任意,都有,
求a的取舍范围。
同课章节目录
