2019年高考浙江卷数学真题试卷(解析版)
文档属性
| 名称 | 2019年高考浙江卷数学真题试卷(解析版) |  | |
| 格式 | rar | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-06-12 16:26:47 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
2019年高考数学真题试卷(浙江卷)原卷+解析
一、选择题:本大题共10小题,每小题4分,共40分。
1.(2019?浙江)已知全集U={-1,0,1,2,3},集合A={0,1,2},B={-1,0,1},则
=(
??)
A.?{-1}????B.?{0,1}????C.?{-1,2,3}????D.?{-1,0,1,3}
【答案】
A
【考点】交、并、补集的混合运算
【解析】【解答】解:
,所以
={-1}.
故答案为:A.
【分析】根据集合的补写出
即可得到
.
2.(2019?浙江)渐近线方程为x±y=0的双曲线的离心率是(
??)
A.???????B.?1?????C.?????????D.?2
【答案】
C
【考点】双曲线的简单性质
【解析】【解答】解:根据双曲线的渐近线方程,得
,所以离心率e=
.
故答案为:C.
【分析】根据双曲线的渐近线方程,得到
,即可求出离心率e.
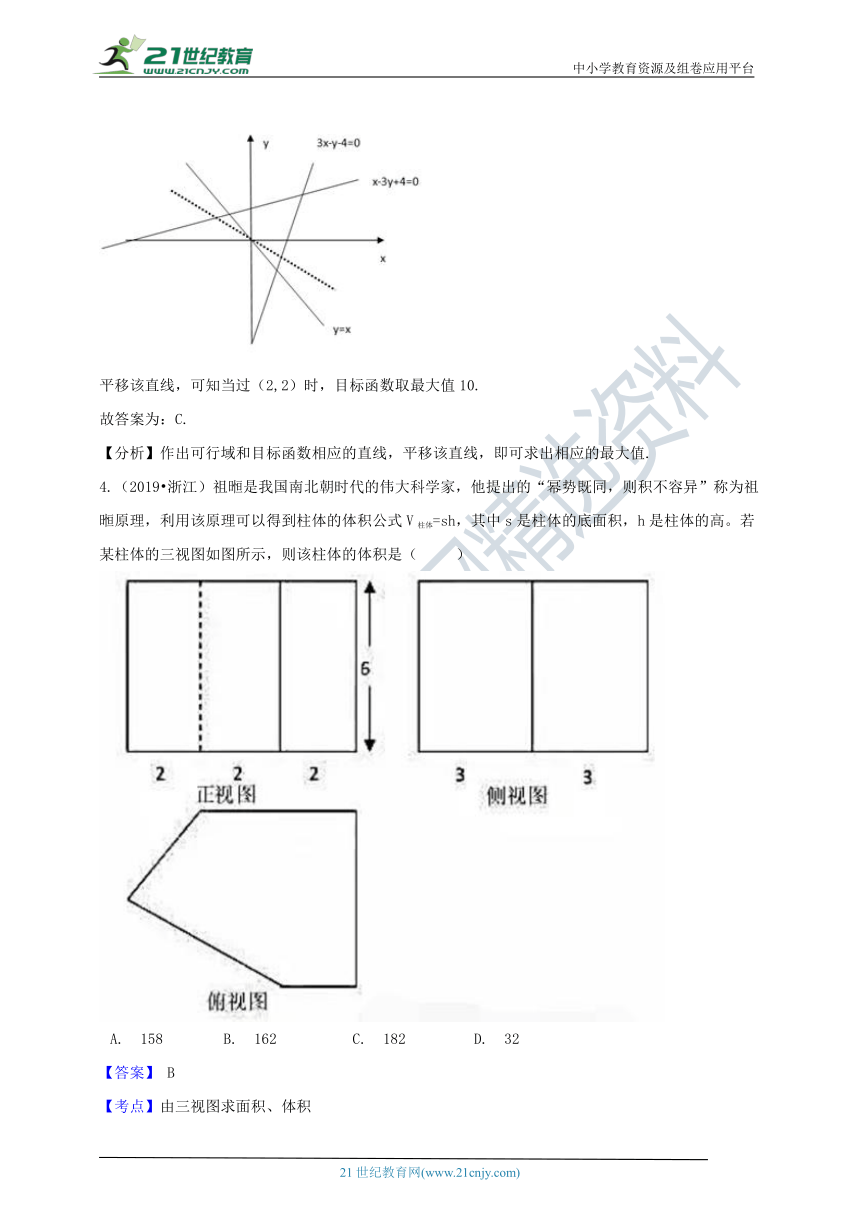
3.(2019?浙江)若实数x,y满足约束条件
,则z=3x+2y的最大值是(
??)
A.?-1???????B.?1???????C.?10?????????D.?12
【答案】
C
【考点】简单线性规划的应用
【解析】【解答】作出可行域和目标函数相应的直线,
平移该直线,可知当过(2,2)时,目标函数取最大值10.
故答案为:C.
【分析】作出可行域和目标函数相应的直线,平移该直线,即可求出相应的最大值.
4.(2019?浙江)祖暅是我国南北朝时代的伟大科学家,他提出的“幂势既同,则积不容异”称为祖暅原理,利用该原理可以得到柱体的体积公式V柱体=sh,其中s是柱体的底面积,h是柱体的高。若某柱体的三视图如图所示,则该柱体的体积是(
??)
A.?158?
??B.?162?????C.?182??
?D.?32
【答案】
B
【考点】由三视图求面积、体积
【解析】【解答】根据三视图,确定几何体为五棱柱,
其底面积
,
所以体积V=27
.
故答案为:B.
【分析】根据三视图确定几何体的结构特征,根据祖暅原理,即可求出相应的体积.
5.(2019?浙江)若a>0,b>0,则“a+b≤4“是“ab≤4”的(
??)
A.?充分不必要条件???
B.?必要不充分条件???????????
C.?充分必要条件?????
D.?既不充分也不必要条件
【答案】
A
【考点】必要条件、充分条件与充要条件的判断
【解析】【解答】作出直线y=4-x和函数
的图象,结合图象的关系,可确定“a+b≤4“是“ab≤4”的充分不必要条件.
故答案为:A.
【分析】作出函数的图象,结合图象确定充分必要性即可.
6.(2019?浙江)在同一直角坐标系中,函数y=
,y=loga(x+
),(a>0且a≠0)的图像可能是(
??)
A????
?
B?
C??????
?D?
【答案】
D
【考点】函数的图象
【解析】【解答】当a>1时,y=
的底数大于0小于1,故过(0,1)单调递减;
y=loga(x+
)过(
,0)单调递增,没有符合条件的图象;
当0的底数大于1,故过(0,1)单调递增;
y=loga(x+
)过(
,0)单调递减;
故答案为:D.
【分析】对a的取值分类讨论,结合指数函数和对数函数的特点,确定函数的图象即可.
7.(2019?浙江)设0<a<1随机变量X的分布列是
X
0
a
1
P
则当a在(0,1)内增大时(
??)
A.?D(X)增大??
B.?D(X)减小?
C.?D(X)先增大后减小??
?D.?D(X)先减小后增大
【答案】
D
【考点】离散型随机变量的期望与方差
【解析】【解答】解:E(X)=
,
,
根据二次函数的单调性,可知D(X)先减小后增大;
故答案为:D.
【分析】根据期望的公式求出E(X),结合方差的计算公式及二次函数的性质即可确定D(X)先减小后增大.
8.(2019?浙江)设三棱锥V-ABC的底面是正三角形,侧棱长均相等,P是棱VA上的点,(不含端点),记直线PB与直线AC所成角为α.直线PB与平面ABC所成角为β.二面角P-AC-B的平面角为γ。则(
??)
A.?β<γ,a
<γ???
B.?β<α,β<γ??????
C.?β<α,γ<α?????D.?α<β
,
γ<β
【答案】
B
【考点】异面直线及其所成的角,直线与平面所成的角,二面角的平面角及求法
【解析】【解答】如图
为
中点,
在底面
的投影为
,则
在底面投影
在线段
上,过
作
垂直
,
易得
,过
作
交
于
,过
作
,交
于
,则
,则
,即
,
,即
,综上所述,
B正确.
故答案为:B
【分析】根据异面直线所成的角、直线与平面所成的角、二面角的概念,以及各种角的计算.应用三角函数知识求解,进而比较大小即可.
9.(2019?浙江)设a,b∈R
,
函数f(x)=
,若函数y=f(x)-ax-b恰有3个零点,则(
??)
A.?a<-1,b<0???B.?a<-1,b>0???C.?
a>-1,b>0???D.?a>-1,b>0
【答案】
C
【考点】函数的零点与方程根的关系
【解析】【解答】原题可转化为
与
,有三个交点.
当
时,
,且
,则
⑴当
时,如图
与
不可能有三个交点(实际上有一个),
排除A,B
⑵当
时,分三种情况,如图
与
若有三个交点,则
,答案选D
下面证明:
时,
时
,
,则
,才能保证至少有两个零点,即
,若另一零点在
.
故答案为:C
【分析】本题综合性较强,注重重要知识、基础知识、运算求解能力、分类讨论思想及数形结合思想的考查.研究函数方程的方法较为灵活,通常需要结合函数的图象加以分析.
10.(2019?浙江)设a,b∈R
,
数列{an},满足an
=a,an+1=
an2+b,b∈N
,
则(
??)
A.?当b=
时,a10>10?
?
B.?当b=
时,a10>10
C.?当b=-2时,a10>10????
?D.?当b=-4时,a10>10
【答案】
A
【考点】数列的函数特性
【解析】【解答】选项B:不动点满足
时,如图,若
,
排除
如图,若
为不动点
则
选项C:不动点满足
,不动点为
,令
,则
,
排除
选项D:不动点满足
,不动点为
,令
,则
,排除.
故答案为:A
【分析】遇到此类问题,可以利用函数方程思想,通过研究函数的不动点,进一步讨论
的可能取值,利用“排除法”求解.
二、填空题:本大题共7小题,多空题每题6分,单空题每题4分,共36分。
11.(2019?浙江)复数
(i为虚数单位),则|z|=________
【答案】
【考点】复数求模
【解析】【解答】解:
,故|z|
;
故答案为
.
【分析】根据复数的除法运算求出z,即可得到|z|.
12.(2019?浙江)已知圆C的圆心坐标是(0,m),半径长是r,若直线2x-y+3=0与圆相切于点A(-2,-1)则m=________,r=________
【答案】
-2;
【考点】圆的切线方程
【解析】【解答】解:圆心与切点连线与直线2x-y+3=0垂直,
所以
,解得m=-2;
根据两点间的距离公式,可得r=
.
【分析】根据圆心与切点连线与切线垂直,结合直线的斜率求出m,根据两点间距离公式求出r即可.
13.(2019?浙江)在二项式(
+x)9的展开式中,常数项是________,系数为有理数的项的个数是________
【答案】
;5
【考点】二项式定理的应用
【解析】【解答】解:展开式的通项
,
当9-r=0,即r=9时,得展开式的常数项为
;
当r=0,2,4,6,8时,展开式的系数为有理数.
【分析】写出展开式的通项,令x的次数为0,即可求出常数项,令r为偶数,则展开式的系数为有理数.
14.(2019?浙江)在△ABC中,∠ABC=90°,AB=4,BC=3,点D在线段AC上,若∠BDC=45°,则BD=________.COS∠ABD=________
【答案】
;
【考点】余弦定理的应用
【解析】【解答】解:在△BCD中,
根据正弦定理
即
解得BD=
;
COS∠ABD=sin
.
【分析】在△BCD中,根据正弦定理即可求出BD;根据两角差的正弦公式,即可求出相应的三角函数值.
15.(2019?浙江)已知椭圆
的左焦点为F,点P在椭圆且在x轴上方,若线段PF的中点在以原点O为圆心,|OF|为半径的圆上,则直线PF的斜率是________
【答案】
【考点】椭圆的应用
【解析】【解答】解:设P(m,n),则
?????
(1)
根据椭圆的方程,得F(-2,0),故PF的中点为(
),
根据中点在以原点O为圆心,|OF|为半径的圆上,得
????
(2)
将(1)和(2)联立得
,
故直线PF的斜率为
.
故答案为.
【分析】根据椭圆的方程F的坐标,设出P,结合题意,求出P点坐标,即可得到PF的斜率.
16.(2019?浙江)已知a∈R
,
函数f(x)=ax3-x,若存在t∈R
,
使得|f(t+2)-f(t)|≤
,则实数a的最大值是________
【答案】
【考点】绝对值三角不等式
【解析】【解答】,
使得令
,则原不等式转化为存在
,由折线函数,如图
只需
,即
,即
的最大值是
【分析】本题主要考查含参绝对值不等式、函数方程思想及数形结合思想,从研究
入手,令
,从而使问题加以转化,通过绘制函数图象,观察得解.
17.(2019?浙江)已知正方形ABCD的边长为1,当每个λi(i=1,2,3,4,5,6)取遍±1时,|λ1
+λ2
+λ3
+λ4
+λ5
+λ6
|的最小值是________,最大值是________
【答案】
0;
【考点】向量在几何中的应用
【解析】【解答】
要使
的最小,只需要
,此时只需要取
此时
等号成立当且仅当
均非负或者均非正,并且
均非负或者均非正。
比如
则
.
【分析】本题主要考查平面向量的应用,题目难度较大.从引入“基向量”入手,简化模的表现形式,利用转化与化归思想将问题逐步简化.
三、解答题:本大题共5小题,共74分。
18.(2019?浙江)设函数f(x)=sinx,x
R。
(1)已知θ=[0,2x),函数f(x+θ)是偶函数,求θ的值
(2)求函数y=[f(x)+
]2+[f(x+
)]2的值域
【答案】
(1)因为
是偶函数,所以,对任意实数x都有
,
即
,
故
,
所以
.
又
,因此
或
.
(2)
.
因此,函数的值域是
.
【考点】正弦函数的奇偶性,正弦函数的定义域和值域
【解析】【分析】(1)根据函数的奇偶性求出余弦值,即可确定角的大小;
(2)根据余弦的二倍角公式,结合辅助角公式及余弦函数的有界性,即可求出函数的值域.
19.(2019?浙江)如图,已知三棱柱ABC-A1B1C1
,
平面A1AC1C⊥平面ABC,∠ABC=90°.∠BAC=30°,A1A=A1C=AC,E,F分别是AC,A1B1的中点
?
(1)证明:EF⊥BC
(2)求直线EF与平面A1BC所成角的余弦值.
【答案】
(1)连接A1E
,
因为A1A=A1C
,
E是AC的中点,所以A1E⊥AC.
又平面A1ACC1⊥平面ABC
,
A1E
平面A1ACC1
,
平面A1ACC1∩平面ABC=AC
,
所以,A1E⊥平面ABC
,
则A1E⊥BC.
又因为A1F∥AB
,
∠ABC=90°,故BC⊥A1F.
所以BC⊥平面A1EF.
因此EF⊥BC.
(2)取BC中点G
,
连接EG
,
GF
,
则EGFA1是平行四边形.
由于A1E⊥平面ABC
,
故AE1⊥EG
,
所以平行四边形EGFA1为矩形.
由(I)得BC⊥平面EGFA1
,
则平面A1BC⊥平面EGFA1
,
所以EF在平面A1BC上的射影在直线A1G上.
连接A1G交EF于O
,
则∠EOG是直线EF与平面A1BC所成的角(或其补角).
不妨设AC=4,则在Rt△A1EG中,A1E=2
,EG=
.
由于O为A1G的中点,故
,
所以
.
因此,直线EF与平面A1BC所成角的余弦值是
.
方法二:
连接A1E
,
因为A1A=A1C
,
E是AC的中点,所以A1E⊥AC.
又平面A1ACC1⊥平面ABC
,
A1E
平面A1ACC1
,
平面A1ACC1∩平面ABC=AC
,
所以,A1E⊥平面ABC.
如图,以点E为原点,分别以射线EC
,
EA1为y
,
z轴的正半轴,建立空间直角坐标系E–xyz.
不妨设AC=4,则
A1(0,0,2
),B(
,1,0),
,
,C(0,2,0).
因此,
,
.
由
得
.
【考点】直线与平面垂直的判定,直线与平面所成的角
【解析】【分析】(1)根据线面垂直的判定定理,证明线面垂直,即可得到线线垂直;
(2)
通过线面垂直,找到直线与平面所成的角,结合余弦定理,求出相应的角即可.
20.(2019?浙江)设等差数列{an}的前n项和为Sn
,
a3=4.a4=S3
,
数列{bn}满足:
对每个n∈N
,
Sn+bn
,
Sn+1+bn、Sn+2+bn成等比数列
(1)求数列{an},{bn}的通项公式
(2)记Cn=
,n∈N
,
证明:C1+C2+…+Cn<2
,n∈N
【答案】
(1)设数列
的公差为d
,
由题意得
,
解得
.
从而
.
由
成等比数列得
.
解得
.
所以
.
(2).
我们用数学归纳法证明.
⑴当n=1时,c1=0<2,不等式成立;
⑵假设
时不等式成立,即
.
那么,当
时,
?
.
即当
时不等式也成立.
根据(1)和(2),不等式
对任意
成立.
【考点】等差数列的通项公式,等比数列的通项公式,数学归纳法
【解析】【分析】(1)根据等差数列的通项公式,解方程,结合等比中项,即可求出相应的表达式;
(2)采用数学归纳法,现在n=1时式子成立,假设n=k时式子成立,再证n=k+1时式子也成立即可.
21.(2019?浙江)如图,已知点F(1,0)为抛物线y2=2px(p>0)的焦点.过点F的直线交抛物线A,B两点,点C在抛物线上,使得△ABC的重心G在x轴上,直线AC交x轴于点Q,且Q在点F右侧,记△AFG,△CQG的面积分别为S1
,
S2.
(1)求P的值及抛物线的准线方程.
(2)求
的最小值及此时点G点坐标.
【答案】
(1)由题意得
,即p=2.
所以,抛物线的准线方程为x=?1.
(2)设
,重心
.令
,则
.
由于直线AB过F
,
故直线AB方程为
,代入
,得
,
故
,即
,所以
.
又由于
及重心G在x轴上,故
,得
.
所以,直线AC方程为
,得
.
由于Q在焦点F的右侧,故
.从而
.
令
,则m>0,
.
当
时,
取得最小值
,此时G(2,0).
【考点】抛物线的应用,直线与圆锥曲线的综合问题
【解析】【分析】(1)根据焦点坐标求出p,即可得到抛物线的准线方程;
(2)设出相应点的坐标及直线方程,将直线方程与抛物线方程联立,根据韦达定理,结合换元法,即可求出相应的最小值.
22.(2019?浙江)已知实数a≠0,设函数f(x)=alnx+
.x>0
(1)当a=-
时,求函数f(x)的单调区间
(2)对任意x∈[
,+∞)均有f(x)≤
,求a的取值范围
【答案】
(1)当
时,
.
,
所以,函数
的单调递减区间为(0,3),单调递增区间为(3,+
).
(2)由
,得
.
当
时,
等价于
.
令
,则
.
设
?,则
.
(i)当
?时,
,则
.
记
,则
.
故
1
0
+
单调递减
极小值
单调递增
所以,
?.
因此,
.
(ii)当
时,
.
令
?,则
,
故
在
上单调递增,所以
.
由(i)得
.
所以,
.
因此
.
由(i)(ii)得对任意
,
,
即对任意
,均有
.
综上所述,所求a的取值范围是
.
【考点】利用导数研究函数的单调性,利用导数研究函数的极值
【解析】【分析】(1)将a=-代入,求导数,结合导数确定函数的单调性即可;
(2)采用换元法,构造函数,求导数,结合导数确定函数的单调性,求出函数的最值,即可求出不等式成立时相应的实数a的取值范围.
试卷分析部分
1.
试卷总体分布分析
总分:150分
分值分布
客观题(占比)
40(26.7%)
主观题(占比)
110(73.3%)
题量分布
客观题(占比)
10(45.5%)
主观题(占比)
12(54.5%)
2.
试卷题量分布分析
大题题型
题目量(占比)
分值(占比)
选择题:本大题共10小题,每小题4分,共40分。
10(45.5%)
40(26.7%)
填空题:本大题共7小题,多空题每题6分,单空题每题4分,共36分。
7(31.8%)
36(24.0%)
解答题:本大题共5小题,共74分。
5(22.7%)
74(49.3%)
3.
试卷难度结构分析
序号
难易度
占比
1
容易
18.2%
2
普通
72.7%
3
困难
9.1%
4.
试卷知识点分析
序号
知识点(认知水平)
分值(占比)
对应题号
1
交、并、补集的混合运算
4(1.6%)
1
2
双曲线的简单性质
4(1.6%)
2
3
简单线性规划的应用
4(1.6%)
3
4
由三视图求面积、体积
4(1.6%)
4
5
必要条件、充分条件与充要条件的判断
4(1.6%)
5
6
函数的图象
4(1.6%)
6
7
离散型随机变量的期望与方差
4(1.6%)
7
8
直线与平面所成的角
19(7.7%)
8,19
9
异面直线及其所成的角
4(1.6%)
8
10
二面角的平面角及求法
4(1.6%)
8
11
函数的零点与方程根的关系
4(1.6%)
9
12
数列的函数特性
4(1.6%)
10
13
复数求模
4(1.6%)
11
14
圆的切线方程
6(2.4%)
12
15
二项式定理的应用
6(2.4%)
13
16
余弦定理的应用
6(2.4%)
14
17
椭圆的应用
4(1.6%)
15
18
绝对值三角不等式
4(1.6%)
16
19
向量在几何中的应用
6(2.4%)
17
20
正弦函数的奇偶性
14(5.7%)
18
21
正弦函数的定义域和值域
14(5.7%)
18
22
直线与平面垂直的判定
15(6.1%)
19
23
数学归纳法
15(6.1%)
20
24
等差数列的通项公式
15(6.1%)
20
25
等比数列的通项公式
15(6.1%)
20
26
直线与圆锥曲线的综合问题
15(6.1%)
21
27
抛物线的应用
15(6.1%)
21
28
利用导数研究函数的单调性
15(6.1%)
22
29
利用导数研究函数的极值
15(6.1%)
22
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)
2019年高考数学真题试卷(浙江卷)原卷+解析
一、选择题:本大题共10小题,每小题4分,共40分。
1.(2019?浙江)已知全集U={-1,0,1,2,3},集合A={0,1,2},B={-1,0,1},则
=(
??)
A.?{-1}????B.?{0,1}????C.?{-1,2,3}????D.?{-1,0,1,3}
【答案】
A
【考点】交、并、补集的混合运算
【解析】【解答】解:
,所以
={-1}.
故答案为:A.
【分析】根据集合的补写出
即可得到
.
2.(2019?浙江)渐近线方程为x±y=0的双曲线的离心率是(
??)
A.???????B.?1?????C.?????????D.?2
【答案】
C
【考点】双曲线的简单性质
【解析】【解答】解:根据双曲线的渐近线方程,得
,所以离心率e=
.
故答案为:C.
【分析】根据双曲线的渐近线方程,得到
,即可求出离心率e.
3.(2019?浙江)若实数x,y满足约束条件
,则z=3x+2y的最大值是(
??)
A.?-1???????B.?1???????C.?10?????????D.?12
【答案】
C
【考点】简单线性规划的应用
【解析】【解答】作出可行域和目标函数相应的直线,
平移该直线,可知当过(2,2)时,目标函数取最大值10.
故答案为:C.
【分析】作出可行域和目标函数相应的直线,平移该直线,即可求出相应的最大值.
4.(2019?浙江)祖暅是我国南北朝时代的伟大科学家,他提出的“幂势既同,则积不容异”称为祖暅原理,利用该原理可以得到柱体的体积公式V柱体=sh,其中s是柱体的底面积,h是柱体的高。若某柱体的三视图如图所示,则该柱体的体积是(
??)
A.?158?
??B.?162?????C.?182??
?D.?32
【答案】
B
【考点】由三视图求面积、体积
【解析】【解答】根据三视图,确定几何体为五棱柱,
其底面积
,
所以体积V=27
.
故答案为:B.
【分析】根据三视图确定几何体的结构特征,根据祖暅原理,即可求出相应的体积.
5.(2019?浙江)若a>0,b>0,则“a+b≤4“是“ab≤4”的(
??)
A.?充分不必要条件???
B.?必要不充分条件???????????
C.?充分必要条件?????
D.?既不充分也不必要条件
【答案】
A
【考点】必要条件、充分条件与充要条件的判断
【解析】【解答】作出直线y=4-x和函数
的图象,结合图象的关系,可确定“a+b≤4“是“ab≤4”的充分不必要条件.
故答案为:A.
【分析】作出函数的图象,结合图象确定充分必要性即可.
6.(2019?浙江)在同一直角坐标系中,函数y=
,y=loga(x+
),(a>0且a≠0)的图像可能是(
??)
A????
?
B?
C??????
?D?
【答案】
D
【考点】函数的图象
【解析】【解答】当a>1时,y=
的底数大于0小于1,故过(0,1)单调递减;
y=loga(x+
)过(
,0)单调递增,没有符合条件的图象;
当0
y=loga(x+
)过(
,0)单调递减;
故答案为:D.
【分析】对a的取值分类讨论,结合指数函数和对数函数的特点,确定函数的图象即可.
7.(2019?浙江)设0<a<1随机变量X的分布列是
X
0
a
1
P
则当a在(0,1)内增大时(
??)
A.?D(X)增大??
B.?D(X)减小?
C.?D(X)先增大后减小??
?D.?D(X)先减小后增大
【答案】
D
【考点】离散型随机变量的期望与方差
【解析】【解答】解:E(X)=
,
,
根据二次函数的单调性,可知D(X)先减小后增大;
故答案为:D.
【分析】根据期望的公式求出E(X),结合方差的计算公式及二次函数的性质即可确定D(X)先减小后增大.
8.(2019?浙江)设三棱锥V-ABC的底面是正三角形,侧棱长均相等,P是棱VA上的点,(不含端点),记直线PB与直线AC所成角为α.直线PB与平面ABC所成角为β.二面角P-AC-B的平面角为γ。则(
??)
A.?β<γ,a
<γ???
B.?β<α,β<γ??????
C.?β<α,γ<α?????D.?α<β
,
γ<β
【答案】
B
【考点】异面直线及其所成的角,直线与平面所成的角,二面角的平面角及求法
【解析】【解答】如图
为
中点,
在底面
的投影为
,则
在底面投影
在线段
上,过
作
垂直
,
易得
,过
作
交
于
,过
作
,交
于
,则
,则
,即
,
,即
,综上所述,
B正确.
故答案为:B
【分析】根据异面直线所成的角、直线与平面所成的角、二面角的概念,以及各种角的计算.应用三角函数知识求解,进而比较大小即可.
9.(2019?浙江)设a,b∈R
,
函数f(x)=
,若函数y=f(x)-ax-b恰有3个零点,则(
??)
A.?a<-1,b<0???B.?a<-1,b>0???C.?
a>-1,b>0???D.?a>-1,b>0
【答案】
C
【考点】函数的零点与方程根的关系
【解析】【解答】原题可转化为
与
,有三个交点.
当
时,
,且
,则
⑴当
时,如图
与
不可能有三个交点(实际上有一个),
排除A,B
⑵当
时,分三种情况,如图
与
若有三个交点,则
,答案选D
下面证明:
时,
时
,
,则
,才能保证至少有两个零点,即
,若另一零点在
.
故答案为:C
【分析】本题综合性较强,注重重要知识、基础知识、运算求解能力、分类讨论思想及数形结合思想的考查.研究函数方程的方法较为灵活,通常需要结合函数的图象加以分析.
10.(2019?浙江)设a,b∈R
,
数列{an},满足an
=a,an+1=
an2+b,b∈N
,
则(
??)
A.?当b=
时,a10>10?
?
B.?当b=
时,a10>10
C.?当b=-2时,a10>10????
?D.?当b=-4时,a10>10
【答案】
A
【考点】数列的函数特性
【解析】【解答】选项B:不动点满足
时,如图,若
,
排除
如图,若
为不动点
则
选项C:不动点满足
,不动点为
,令
,则
,
排除
选项D:不动点满足
,不动点为
,令
,则
,排除.
故答案为:A
【分析】遇到此类问题,可以利用函数方程思想,通过研究函数的不动点,进一步讨论
的可能取值,利用“排除法”求解.
二、填空题:本大题共7小题,多空题每题6分,单空题每题4分,共36分。
11.(2019?浙江)复数
(i为虚数单位),则|z|=________
【答案】
【考点】复数求模
【解析】【解答】解:
,故|z|
;
故答案为
.
【分析】根据复数的除法运算求出z,即可得到|z|.
12.(2019?浙江)已知圆C的圆心坐标是(0,m),半径长是r,若直线2x-y+3=0与圆相切于点A(-2,-1)则m=________,r=________
【答案】
-2;
【考点】圆的切线方程
【解析】【解答】解:圆心与切点连线与直线2x-y+3=0垂直,
所以
,解得m=-2;
根据两点间的距离公式,可得r=
.
【分析】根据圆心与切点连线与切线垂直,结合直线的斜率求出m,根据两点间距离公式求出r即可.
13.(2019?浙江)在二项式(
+x)9的展开式中,常数项是________,系数为有理数的项的个数是________
【答案】
;5
【考点】二项式定理的应用
【解析】【解答】解:展开式的通项
,
当9-r=0,即r=9时,得展开式的常数项为
;
当r=0,2,4,6,8时,展开式的系数为有理数.
【分析】写出展开式的通项,令x的次数为0,即可求出常数项,令r为偶数,则展开式的系数为有理数.
14.(2019?浙江)在△ABC中,∠ABC=90°,AB=4,BC=3,点D在线段AC上,若∠BDC=45°,则BD=________.COS∠ABD=________
【答案】
;
【考点】余弦定理的应用
【解析】【解答】解:在△BCD中,
根据正弦定理
即
解得BD=
;
COS∠ABD=sin
.
【分析】在△BCD中,根据正弦定理即可求出BD;根据两角差的正弦公式,即可求出相应的三角函数值.
15.(2019?浙江)已知椭圆
的左焦点为F,点P在椭圆且在x轴上方,若线段PF的中点在以原点O为圆心,|OF|为半径的圆上,则直线PF的斜率是________
【答案】
【考点】椭圆的应用
【解析】【解答】解:设P(m,n),则
?????
(1)
根据椭圆的方程,得F(-2,0),故PF的中点为(
),
根据中点在以原点O为圆心,|OF|为半径的圆上,得
????
(2)
将(1)和(2)联立得
,
故直线PF的斜率为
.
故答案为.
【分析】根据椭圆的方程F的坐标,设出P,结合题意,求出P点坐标,即可得到PF的斜率.
16.(2019?浙江)已知a∈R
,
函数f(x)=ax3-x,若存在t∈R
,
使得|f(t+2)-f(t)|≤
,则实数a的最大值是________
【答案】
【考点】绝对值三角不等式
【解析】【解答】,
使得令
,则原不等式转化为存在
,由折线函数,如图
只需
,即
,即
的最大值是
【分析】本题主要考查含参绝对值不等式、函数方程思想及数形结合思想,从研究
入手,令
,从而使问题加以转化,通过绘制函数图象,观察得解.
17.(2019?浙江)已知正方形ABCD的边长为1,当每个λi(i=1,2,3,4,5,6)取遍±1时,|λ1
+λ2
+λ3
+λ4
+λ5
+λ6
|的最小值是________,最大值是________
【答案】
0;
【考点】向量在几何中的应用
【解析】【解答】
要使
的最小,只需要
,此时只需要取
此时
等号成立当且仅当
均非负或者均非正,并且
均非负或者均非正。
比如
则
.
【分析】本题主要考查平面向量的应用,题目难度较大.从引入“基向量”入手,简化模的表现形式,利用转化与化归思想将问题逐步简化.
三、解答题:本大题共5小题,共74分。
18.(2019?浙江)设函数f(x)=sinx,x
R。
(1)已知θ=[0,2x),函数f(x+θ)是偶函数,求θ的值
(2)求函数y=[f(x)+
]2+[f(x+
)]2的值域
【答案】
(1)因为
是偶函数,所以,对任意实数x都有
,
即
,
故
,
所以
.
又
,因此
或
.
(2)
.
因此,函数的值域是
.
【考点】正弦函数的奇偶性,正弦函数的定义域和值域
【解析】【分析】(1)根据函数的奇偶性求出余弦值,即可确定角的大小;
(2)根据余弦的二倍角公式,结合辅助角公式及余弦函数的有界性,即可求出函数的值域.
19.(2019?浙江)如图,已知三棱柱ABC-A1B1C1
,
平面A1AC1C⊥平面ABC,∠ABC=90°.∠BAC=30°,A1A=A1C=AC,E,F分别是AC,A1B1的中点
?
(1)证明:EF⊥BC
(2)求直线EF与平面A1BC所成角的余弦值.
【答案】
(1)连接A1E
,
因为A1A=A1C
,
E是AC的中点,所以A1E⊥AC.
又平面A1ACC1⊥平面ABC
,
A1E
平面A1ACC1
,
平面A1ACC1∩平面ABC=AC
,
所以,A1E⊥平面ABC
,
则A1E⊥BC.
又因为A1F∥AB
,
∠ABC=90°,故BC⊥A1F.
所以BC⊥平面A1EF.
因此EF⊥BC.
(2)取BC中点G
,
连接EG
,
GF
,
则EGFA1是平行四边形.
由于A1E⊥平面ABC
,
故AE1⊥EG
,
所以平行四边形EGFA1为矩形.
由(I)得BC⊥平面EGFA1
,
则平面A1BC⊥平面EGFA1
,
所以EF在平面A1BC上的射影在直线A1G上.
连接A1G交EF于O
,
则∠EOG是直线EF与平面A1BC所成的角(或其补角).
不妨设AC=4,则在Rt△A1EG中,A1E=2
,EG=
.
由于O为A1G的中点,故
,
所以
.
因此,直线EF与平面A1BC所成角的余弦值是
.
方法二:
连接A1E
,
因为A1A=A1C
,
E是AC的中点,所以A1E⊥AC.
又平面A1ACC1⊥平面ABC
,
A1E
平面A1ACC1
,
平面A1ACC1∩平面ABC=AC
,
所以,A1E⊥平面ABC.
如图,以点E为原点,分别以射线EC
,
EA1为y
,
z轴的正半轴,建立空间直角坐标系E–xyz.
不妨设AC=4,则
A1(0,0,2
),B(
,1,0),
,
,C(0,2,0).
因此,
,
.
由
得
.
【考点】直线与平面垂直的判定,直线与平面所成的角
【解析】【分析】(1)根据线面垂直的判定定理,证明线面垂直,即可得到线线垂直;
(2)
通过线面垂直,找到直线与平面所成的角,结合余弦定理,求出相应的角即可.
20.(2019?浙江)设等差数列{an}的前n项和为Sn
,
a3=4.a4=S3
,
数列{bn}满足:
对每个n∈N
,
Sn+bn
,
Sn+1+bn、Sn+2+bn成等比数列
(1)求数列{an},{bn}的通项公式
(2)记Cn=
,n∈N
,
证明:C1+C2+…+Cn<2
,n∈N
【答案】
(1)设数列
的公差为d
,
由题意得
,
解得
.
从而
.
由
成等比数列得
.
解得
.
所以
.
(2).
我们用数学归纳法证明.
⑴当n=1时,c1=0<2,不等式成立;
⑵假设
时不等式成立,即
.
那么,当
时,
?
.
即当
时不等式也成立.
根据(1)和(2),不等式
对任意
成立.
【考点】等差数列的通项公式,等比数列的通项公式,数学归纳法
【解析】【分析】(1)根据等差数列的通项公式,解方程,结合等比中项,即可求出相应的表达式;
(2)采用数学归纳法,现在n=1时式子成立,假设n=k时式子成立,再证n=k+1时式子也成立即可.
21.(2019?浙江)如图,已知点F(1,0)为抛物线y2=2px(p>0)的焦点.过点F的直线交抛物线A,B两点,点C在抛物线上,使得△ABC的重心G在x轴上,直线AC交x轴于点Q,且Q在点F右侧,记△AFG,△CQG的面积分别为S1
,
S2.
(1)求P的值及抛物线的准线方程.
(2)求
的最小值及此时点G点坐标.
【答案】
(1)由题意得
,即p=2.
所以,抛物线的准线方程为x=?1.
(2)设
,重心
.令
,则
.
由于直线AB过F
,
故直线AB方程为
,代入
,得
,
故
,即
,所以
.
又由于
及重心G在x轴上,故
,得
.
所以,直线AC方程为
,得
.
由于Q在焦点F的右侧,故
.从而
.
令
,则m>0,
.
当
时,
取得最小值
,此时G(2,0).
【考点】抛物线的应用,直线与圆锥曲线的综合问题
【解析】【分析】(1)根据焦点坐标求出p,即可得到抛物线的准线方程;
(2)设出相应点的坐标及直线方程,将直线方程与抛物线方程联立,根据韦达定理,结合换元法,即可求出相应的最小值.
22.(2019?浙江)已知实数a≠0,设函数f(x)=alnx+
.x>0
(1)当a=-
时,求函数f(x)的单调区间
(2)对任意x∈[
,+∞)均有f(x)≤
,求a的取值范围
【答案】
(1)当
时,
.
,
所以,函数
的单调递减区间为(0,3),单调递增区间为(3,+
).
(2)由
,得
.
当
时,
等价于
.
令
,则
.
设
?,则
.
(i)当
?时,
,则
.
记
,则
.
故
1
0
+
单调递减
极小值
单调递增
所以,
?.
因此,
.
(ii)当
时,
.
令
?,则
,
故
在
上单调递增,所以
.
由(i)得
.
所以,
.
因此
.
由(i)(ii)得对任意
,
,
即对任意
,均有
.
综上所述,所求a的取值范围是
.
【考点】利用导数研究函数的单调性,利用导数研究函数的极值
【解析】【分析】(1)将a=-代入,求导数,结合导数确定函数的单调性即可;
(2)采用换元法,构造函数,求导数,结合导数确定函数的单调性,求出函数的最值,即可求出不等式成立时相应的实数a的取值范围.
试卷分析部分
1.
试卷总体分布分析
总分:150分
分值分布
客观题(占比)
40(26.7%)
主观题(占比)
110(73.3%)
题量分布
客观题(占比)
10(45.5%)
主观题(占比)
12(54.5%)
2.
试卷题量分布分析
大题题型
题目量(占比)
分值(占比)
选择题:本大题共10小题,每小题4分,共40分。
10(45.5%)
40(26.7%)
填空题:本大题共7小题,多空题每题6分,单空题每题4分,共36分。
7(31.8%)
36(24.0%)
解答题:本大题共5小题,共74分。
5(22.7%)
74(49.3%)
3.
试卷难度结构分析
序号
难易度
占比
1
容易
18.2%
2
普通
72.7%
3
困难
9.1%
4.
试卷知识点分析
序号
知识点(认知水平)
分值(占比)
对应题号
1
交、并、补集的混合运算
4(1.6%)
1
2
双曲线的简单性质
4(1.6%)
2
3
简单线性规划的应用
4(1.6%)
3
4
由三视图求面积、体积
4(1.6%)
4
5
必要条件、充分条件与充要条件的判断
4(1.6%)
5
6
函数的图象
4(1.6%)
6
7
离散型随机变量的期望与方差
4(1.6%)
7
8
直线与平面所成的角
19(7.7%)
8,19
9
异面直线及其所成的角
4(1.6%)
8
10
二面角的平面角及求法
4(1.6%)
8
11
函数的零点与方程根的关系
4(1.6%)
9
12
数列的函数特性
4(1.6%)
10
13
复数求模
4(1.6%)
11
14
圆的切线方程
6(2.4%)
12
15
二项式定理的应用
6(2.4%)
13
16
余弦定理的应用
6(2.4%)
14
17
椭圆的应用
4(1.6%)
15
18
绝对值三角不等式
4(1.6%)
16
19
向量在几何中的应用
6(2.4%)
17
20
正弦函数的奇偶性
14(5.7%)
18
21
正弦函数的定义域和值域
14(5.7%)
18
22
直线与平面垂直的判定
15(6.1%)
19
23
数学归纳法
15(6.1%)
20
24
等差数列的通项公式
15(6.1%)
20
25
等比数列的通项公式
15(6.1%)
20
26
直线与圆锥曲线的综合问题
15(6.1%)
21
27
抛物线的应用
15(6.1%)
21
28
利用导数研究函数的单调性
15(6.1%)
22
29
利用导数研究函数的极值
15(6.1%)
22
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)
同课章节目录
