2019年高考全国Ⅰ卷文数真题试卷(解析版)
文档属性
| 名称 | 2019年高考全国Ⅰ卷文数真题试卷(解析版) |  | |
| 格式 | zip | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-06-09 21:22:33 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
2019年高考文数真题试卷(全国Ⅰ卷)
一、选择题:本题共12小题,每小题5分,共60分。在每小题检出的四个选项中,只有一项是符合题目要求的。
1.(2019?卷Ⅰ)设z=,则|z|=(
)
A.2
B.
C.
D.1
【答案】C
【解析】【解答】
【分析】利用复数的混合运算法则求出复数z,再利用复数的实部和虚部求出复数的模。
2.(2019?卷Ⅰ)已知集合U=,A=,B=则=(
)
A.
B.
C.
D.
【答案】C
【解析】【解答】
U=,A=,
B=,
【分析】利用补集的运算法则求出集合再利用交集的运算法则求出集合
3.
(2019?卷Ⅰ)已知a=log20.2,b=20.2,c=0.20.3,则(
)
A.
a<b<c
B.
a<c<b
C.
c<a<b
D.
b<c<a
【答案】B
【解析】【解答】
因为函数中底数为2,又利用增函数的性质,
因为函数中底数为2,又利用增函数的性质,
因为函数中底数为0.2,又利用减函数的性质,
【分析】利用指数函数和对数函数的单调性结合a,b,c与特殊值的大小关系式,判断出a,b,c的大小关系。
4.
(2019?卷Ⅰ)古希腊时期,人们认为最美人体的头顶至肚脐的长度与肚脐至足底的长度之比是,成为黄金分割比例),著名的“断臂维纳斯“便是如此。此外,最美人体的头顶至咽喉的长度与咽喉至肚脐的长度也是。若某人满足上述两个黄金分割比例,且腿长为105cm,头顶至脖子下端的长度为26cm,则其身高可能是(
)
A.165
cm
B.175
cm
C.185cm
D.190
cm
【答案】B
【解析】【解答】
因为头顶至肚脐的长度与肚脐至足底的长度之比是,成为黄金分割比例),此外,头顶至咽喉的长度与咽喉至肚脐的长度也是,所以设咽喉到肚脐的长度为厘米,肚脐到腰的长度为厘米,依题意得:
所以身高为所以最接近的身高是175厘米。
【分析】利用黄金比例的概念结合对应边成比例求出某人满足要求最接近的身高。
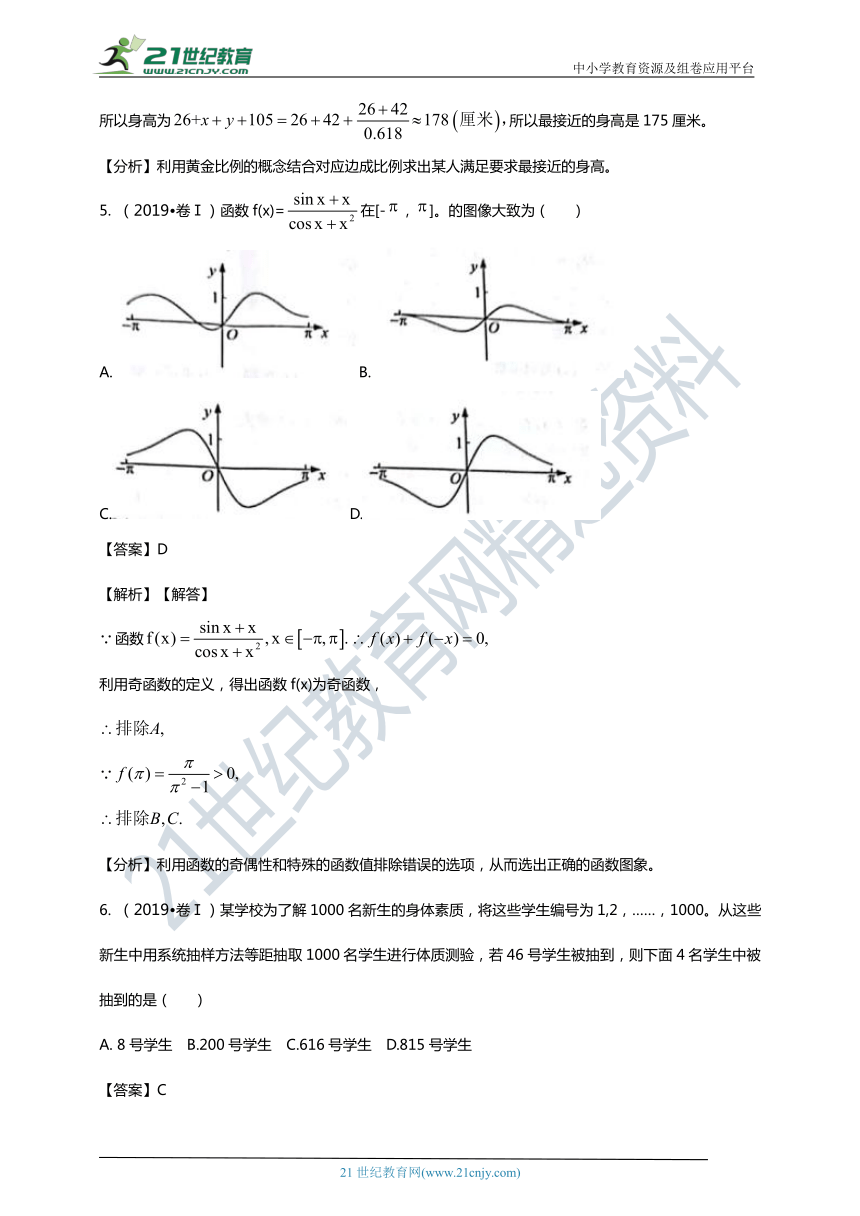
5.
(2019?卷Ⅰ)函数f(x)=在[-,]。的图像大致为(
)
A.B.
C.D.
【答案】D
【解析】【解答】
函数
利用奇函数的定义,得出函数f(x)为奇函数,
【分析】利用函数的奇偶性和特殊的函数值排除错误的选项,从而选出正确的函数图象。
6.
(2019?卷Ⅰ)某学校为了解1000名新生的身体素质,将这些学生编号为1,2,……,1000。从这些新生中用系统抽样方法等距抽取1000名学生进行体质测验,若46号学生被抽到,则下面4名学生中被抽到的是(
)
A.
8号学生
B.200号学生
C.616号学生
D.815号学生
【答案】C
【解析】【解答】
将1000名学生按10人一组分成100组,第一组抽中6号,第二组抽中16号,
以此类推第四组抽中46号,按照等差数列通项公式求解数列中的项的方法,
【分析】将实际问题转化为等差数列的问题,利用系统抽样按组距抽样的方法结合等差数列通项公式求出被抽到的学生号数。
7.
(2019?卷Ⅰ)tan255°=(
)
A.
B.
C.
D.
【答案】D
【解析】【解答】
【分析】利用诱导公式结合两角和的正切公式求出的值。
8.
(2019?卷Ⅰ)已知非零向量,满足||=2|
|,且,则与的夹角为(
)
A.B.
C.
D.
【答案】B
【解析】【解答】
设与的夹角为
【分析】利用向量垂直数量积为0的等价关系,用数量积公式结合已知条件和两向量间夹角的取值范围求出与的夹角。
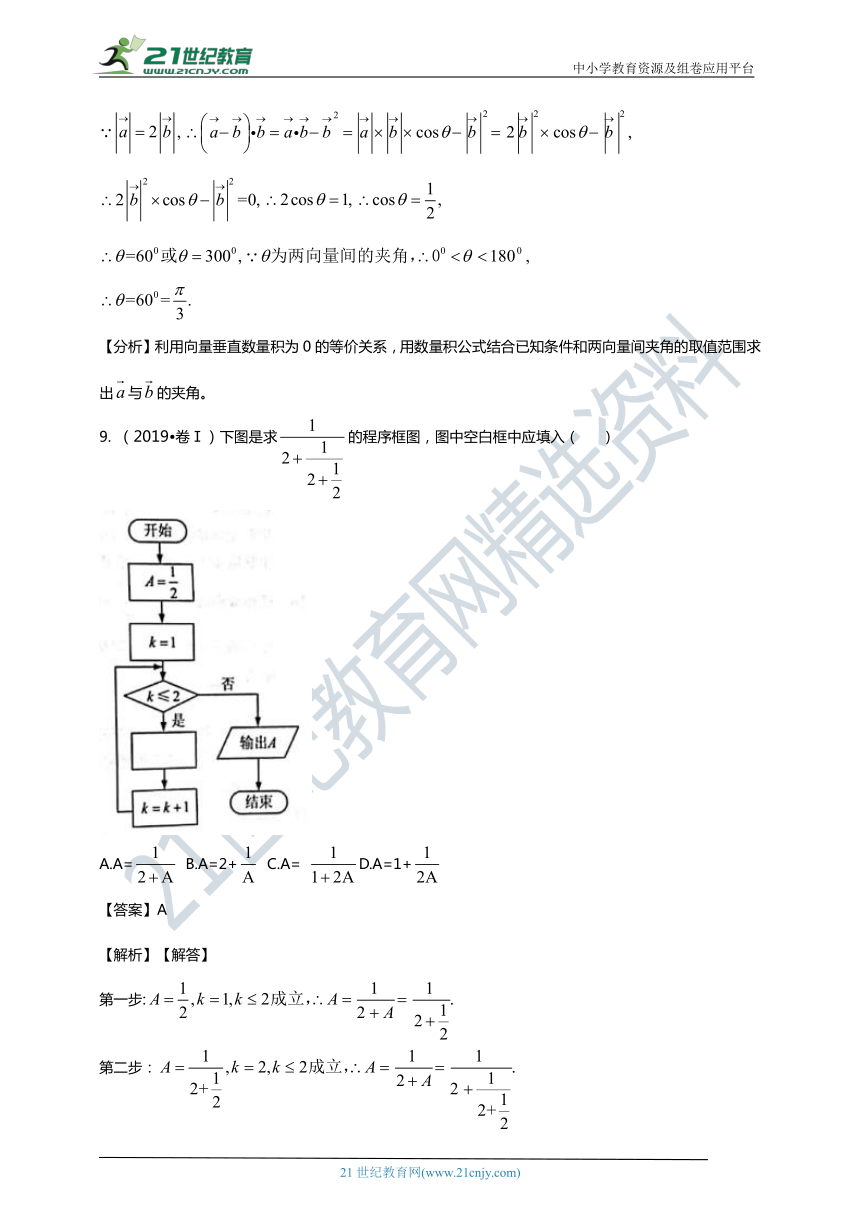
9.
(2019?卷Ⅰ)下图是求的程序框图,图中空白框中应填入(
)
A.A=
B.A=2+
C.A=
D.A=1+
【答案】A
【解析】【解答】
第一步:
第二步:
第三步:
因为输出的A的值满足题意输得的结果,所以判断框里应该填
【分析】利用已知条件结合程序框图的顺序结构、条件结构和循环结构求出满足要求的结果,从而确定判断框里所填的选项。
10.
(2019?卷Ⅰ)双曲线C:(a>0,b>0)的一条渐近线的倾斜角为130°,则C的离心率为(
)
A.2sin40°
B.2cos40°
C.
D.
【答案】D
【解析】【解答】
由双曲线的标准方程(a>0,b>0)得双曲线的一条渐近线方程为:
因为双曲线C:(a>0,b>0)的一条渐近线的倾斜角为130°,根据直线的斜率与直线的倾斜角的关系式,得:
利用同角三角函数基本关系式,得:
【分析】利用双曲线标准方程求出其一条渐近线方程,再利用直线的斜率与倾斜角的关系式找出与倾斜角的关系式,再利用双曲线中a,b,c三者的关系式结合双曲线中离心率公式变形,用同角三角函数的基本关系式化简求出双曲线的离心率。
11.
(2019?卷Ⅰ)?ABC的内角A,B,C的对边分别为a,b,c,已知asinA-bsinB=4csinC,cosA=,则=(
)
A.6
B.5
C.4
D.3
【答案】A
【解析】【解答】
由已知条件结合正弦定理,
①
利用余弦定理,得②
①②联立得:
【分析】利用已知条件结合正弦定理和余弦定理,变形得出b,c的关系式,从而求出的值。
12.
(2019?卷Ⅰ)已知椭圆C的焦点为F1(-1,0),F2(1,0)。过F2的直线与C交于A,B两点。若|AF1|=2|F2B|,|AB|=|BF1|,则C的方程为(
)
A.
+y2=1
B.
+=1
C.
+=1
D.
+=1
【答案】B
【解析】【解答】
如图,对角B用两次余弦定理,得:
得:
【分析】利用双曲线和三角形的图象的位置关系,结合双曲线的定义,对角B用两次余弦定理求出的值,从而求出双曲线的标准方程。
ニ、填空题;本题共4小题,每小题5分,共20分。
13.
(2019?卷Ⅰ)曲线在点处的切线方程为
.
【答案】
【解析】【解答】
设曲线y=3(x2+x)ex在点(0,0)处的切线方程为:
因为曲线y=3(x2+x)ex
,
【分析】利用求导的方法求出曲线在切点处的切线的斜率,再利用点斜式求出曲线y=3(x2+x)ex在点(0,0)处的切线方程。
14.
(2019?卷Ⅰ)记Sn为等比数列{an}的前n项和。若a1=,,则S4=
【答案】
【解析】【解答】
设等比数列的公比为q,利用等比数列的前n项和公式,
当时,
当时,
由求根公式求出q的值,根据题意,从而确定q的值。
【分析】利用分类讨论的方法结合等比数列前n项和公式求出q的值,从而利用与的关系式结合的值求出的值。
15.
(2019?卷Ⅰ)函数f(x)=sin(2x+)-3cosx的最小值为
.
【答案】-4
【解析】【解答】
利用诱导公式和二倍角的余弦公式得:利用换元法,令
当时,
【分析】利用诱导公式和二倍角的余弦公式化简将函数转化为二次函数,再利用二次函数求最值的方法求出函数的最小值。
16.
(2019?卷Ⅰ)已知ACB=90°,P为平面ABC外一点,PC=2,点P到ACB两边AC,BC的距离均为,那么P到平面ABC的距离为
。
【答案】
【解析】【解答】
设点P在平面ABC的距离为d,设点P在平面ABC投影点为O,所以d=PO,过点P作BC边的垂线,垂足为D,连接OP,OC,OD,则即为PC与平面ABC所成的平面角,因为点P到ACB两边AC,BC的距离均为,故点O在ACB的角平分线上,即由于PC=2,则三角形PCD在地底面上的投影三角形OCD为等腰直角三角形,
利用勾股定理得:
点P在平面ABC投影点为O,
所以三角形POC是直角三角形,利用勾股定理得:
【分析】利用投影原理结合线面垂直的定义证出线线垂直,再利用线线垂直满足勾股定理,用勾股定理求出点P在平面ABC的距离。
三、解答题:共70分。解答应写出文字说明,证明过程或演算步骤。第17~21题为必考题,每个试题考生都必须作答,第22、23题为选考题,考生根据要求作答。
17.
(2019?卷Ⅰ)某商场为提高服务质量,随机调查了50名男顾客和50名女顾客,每位顾客对该商场的服务给出满意或不满意的评价,得到下面列联表:
满意
不满意
男顾客
40
10
女顾客
30
20
(1)分别估计男、女顾客对该商场服务满意的概率;
【解析】【解答】
由调查数据,男顾客中对该商场服务满意的比率为,因此男顾客对该商场服务满意的概率的估计值为0.8,女顾客中对该商场服务满意的比率为,因此女顾客对该商场服务满意的概率的估计值为0.6。
(2)能否有95%的把握认为男、女顾客对该商场服务的评价有差异?
附:K2=
P(K2≧k)
0.050
0.010
0.001
k
3.841
6.635
10.828
【解析】【解答】
(2).
由于,故有95%的把握认为男、女顾客对该商场服务的评价有差异.
【分析】(1)根据实际问题的已知条件结合的列联表,用的公式估计出男、女顾客对该商场服务满意的概率。
(2)根据实际问题的已知条件结合的列联表,用独立性检验的方法判断出有95%的把握认为男、女顾客对该商场服务的评价有差异。
18.
(2019?卷Ⅰ)记Sn为等差数列{an}的前n项和,已知Sn=-a5
(1)若a3=4,求{an}的通项公式。
【解析】【解答】
(1)设的公差为d.
由得.
由a3=4得.
于是.
因此的通项公式为.
(2)若a1≥0,求使得Sn≥an的n取值范围。
【解析】【解答】
(2)由(1)得,故.
由知,故等价于,解得1≤n≤10.
所以n的取值范围是.
【分析】(1)利用等差数列的通项公式和等差数列的前n项和公式结合已知条件求出等差数列的首项和公差,从而求出等差数列的通项公式。
由(1)得,故.
由知,故等价于,再利用一元二次不等式求解集的方法结合n自身的取值范围,从而求出n的取值范围。
19.
(2019?卷Ⅰ)如图,直四棱柱ABCD-A1B1C1D1的底面是菱形,AA1=4,AB=2,BAD=60°,E,M,N分别是BC,BB1,A1D的中点
证明:MN∥平面C1DE;
【解析】【解答】
(1)连结.因为M,E分别为的中点,所以,且.又因为N为的中点,所以.
由题设知,可得,故,因此四边形MNDE为平行四边形,.又平面,所以MN∥平面.
求点C到平面C1DE的距离。
【解析】【解答】
(2)过C作C1E的垂线,垂足为H.
由已知可得,,所以DE⊥平面,故DE⊥CH.
从而CH⊥平面,故CH的长即为C到平面的距离,
由已知可得CE=1,C1C=4,所以,故.
从而点C到平面的距离为.
【分析】(1)利用直四棱柱的结构特征结合已知条件,用中点作中位线证线线平行,再利用线线相等结合平行四边形的定义证出四边形MNDE为平行四边形,再利用平行四边形的定义证出另一组线线平行,从而用线线平行结合线面平行的判定定理证出线面平行。
(2)利用直四棱柱的结构特征结合已知条件,用线面垂直的定义证出线线垂直,再利用线面垂直结合线面垂直的判定定理证出线面垂直,从而推出CH的长即为C到平面的距离,由已知可得CE=1,C1C=4,所以,故从而点C到平面的距离为.
20.
(2019?卷Ⅰ)已知函数f(x)=2sinx-xcosx-x,f‘(x)为f(x)的导数。
(1)证明:f(x)在区间(0,
π)存在唯一零点;
【解析】【解答】
(1)设,则.
当时,;当时,,所以在单调递增,在单调递减.又,故在存在唯一零点.
所以在存在唯一零点.
(2)若x?[0,π]时,f(x)≥ax,求a的取值范围。
【解析】【解答】
(2)由题设知,可得a≤0.
由(1)知,在只有一个零点,设为,且当时,;当时,,所以在单调递增,在单调递减.
又,所以,当时,.
又当时,ax≤0,故.
因此,a的取值范围是.
【分析】(1)利用求导的方法判断函数的单调性,再利用零点存在性定理证出函数在区间(0,
π)存在唯一零点。
(2)由题设知,可得a≤0.
由(1)知,在只有一个零点,
利用求导的方法判断函数的单调性,再利用零点存在性定理求出的取值范围。
21.
(2019?卷Ⅰ)已知点A,B关于坐标原点O对称,|AB|=4,⊙M过点A,B且与直线x+2=0相切。
(1)若A在直线x+y=0上,求⊙M的半径。
【解析】【解答】
因为过点,所以圆心M在AB的垂直平分线上.由已知A在直线上,
且关于坐标原点O对称,所以M在直线上,故可设.
因为与直线x+2=0相切,所以的半径为.
由已知得,又,故可得,解得或.
故的半径或.
(2)是否存在定点P,使得当A运动时,|MA|-|MP|为定值?并说明理由。
【解析】【解答】
(2)存在定点,使得为定值.
理由如下:
设,由已知得的半径为.
由于,故可得,化简得M的轨迹方程为.
因为曲线是以点为焦点,以直线为准线的抛物线,
所以因为,所以存在满足条件的定点P。
【分析】(1)因为过点,利用垂直平分线的性质推出圆心M在AB的垂直平分线上,再由点A在直线上,结合点与点关于点对称的性质和求解方法推出点M在直线上,故可设,再利用直线与圆相切的位置关系的判断方法求出的半径与的关系式,再由已知得,结合两向量垂直,用勾股定理求出的值,从而求出的半径。
(2)设,由已知得的半径为
再由两向量垂直,用勾股定理求出点M的轨迹方程,从而判断出点M的轨迹为抛物线,因为曲线是以点为焦点,以直线为准线的抛物线,再利用抛物线的定义得出因为,所以存在满足条件的定点使得为定值。
四、选考题,共10分。请考生在第22、23题中任选一直作答。如果多做。则按所做的第一题计分。
22.
(2019?卷Ⅰ)在直角坐标系xOy中,曲线C的参数方程为(t为参数)。以坐标原点O为极点,x轴的正半轴为极轴建立极坐标系,直线l的极坐标方程为2ρcosθ+ρsinθ+11=0。
(1)求C和l的直角坐标方程;
【解析】【解答】
因为,且,
所以C的直角坐标方程为.
.
(2)求C上的点到l距离的最小值。
【解析】【解答】
(2)由(1)可设曲线C的参数方程为(为参数,).
曲线C上的点到的距离为.
当时,取得最小值7,故C上的点到距离的最小值为.
【分析】(1)利用参数方程转化为直角坐标方程的方法结合极坐标与直角坐标的互化公式求出曲线C和直线的直角坐标方程。
(2)利用参数表示满足曲线C上的点的坐标,再利用点到直线的距离公式结合辅助角公式化简转化为三角型函数,再利用还原法将三角型函数转化为余弦函数,再利用余弦函数的图象求出三角型函数的最小值,从而求出曲线C上的点到直线的距离的最小值。
23.
(2019?卷Ⅰ)已知a,b,c为正数,且满足abc=1。证明:
(1);
【解析】【解答】
(1)因为,又,故有
.
所以.
(2)(a+b)3+(b+c)3+(c+a)3≥24。
【解析】【解答】
(2)因为为正数且,故有
=24.
所以.
【分析】(1)利用均值不等式求最值的方法结合已知条件变形证出不等式成立。
(2)利用均值不等式求最值的方法结合已知条件变形证出不等式成立。
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)
2019年高考文数真题试卷(全国Ⅰ卷)
一、选择题:本题共12小题,每小题5分,共60分。在每小题检出的四个选项中,只有一项是符合题目要求的。
1.(2019?卷Ⅰ)设z=,则|z|=(
)
A.2
B.
C.
D.1
【答案】C
【解析】【解答】
【分析】利用复数的混合运算法则求出复数z,再利用复数的实部和虚部求出复数的模。
2.(2019?卷Ⅰ)已知集合U=,A=,B=则=(
)
A.
B.
C.
D.
【答案】C
【解析】【解答】
U=,A=,
B=,
【分析】利用补集的运算法则求出集合再利用交集的运算法则求出集合
3.
(2019?卷Ⅰ)已知a=log20.2,b=20.2,c=0.20.3,则(
)
A.
a<b<c
B.
a<c<b
C.
c<a<b
D.
b<c<a
【答案】B
【解析】【解答】
因为函数中底数为2,又利用增函数的性质,
因为函数中底数为2,又利用增函数的性质,
因为函数中底数为0.2,又利用减函数的性质,
【分析】利用指数函数和对数函数的单调性结合a,b,c与特殊值的大小关系式,判断出a,b,c的大小关系。
4.
(2019?卷Ⅰ)古希腊时期,人们认为最美人体的头顶至肚脐的长度与肚脐至足底的长度之比是,成为黄金分割比例),著名的“断臂维纳斯“便是如此。此外,最美人体的头顶至咽喉的长度与咽喉至肚脐的长度也是。若某人满足上述两个黄金分割比例,且腿长为105cm,头顶至脖子下端的长度为26cm,则其身高可能是(
)
A.165
cm
B.175
cm
C.185cm
D.190
cm
【答案】B
【解析】【解答】
因为头顶至肚脐的长度与肚脐至足底的长度之比是,成为黄金分割比例),此外,头顶至咽喉的长度与咽喉至肚脐的长度也是,所以设咽喉到肚脐的长度为厘米,肚脐到腰的长度为厘米,依题意得:
所以身高为所以最接近的身高是175厘米。
【分析】利用黄金比例的概念结合对应边成比例求出某人满足要求最接近的身高。
5.
(2019?卷Ⅰ)函数f(x)=在[-,]。的图像大致为(
)
A.B.
C.D.
【答案】D
【解析】【解答】
函数
利用奇函数的定义,得出函数f(x)为奇函数,
【分析】利用函数的奇偶性和特殊的函数值排除错误的选项,从而选出正确的函数图象。
6.
(2019?卷Ⅰ)某学校为了解1000名新生的身体素质,将这些学生编号为1,2,……,1000。从这些新生中用系统抽样方法等距抽取1000名学生进行体质测验,若46号学生被抽到,则下面4名学生中被抽到的是(
)
A.
8号学生
B.200号学生
C.616号学生
D.815号学生
【答案】C
【解析】【解答】
将1000名学生按10人一组分成100组,第一组抽中6号,第二组抽中16号,
以此类推第四组抽中46号,按照等差数列通项公式求解数列中的项的方法,
【分析】将实际问题转化为等差数列的问题,利用系统抽样按组距抽样的方法结合等差数列通项公式求出被抽到的学生号数。
7.
(2019?卷Ⅰ)tan255°=(
)
A.
B.
C.
D.
【答案】D
【解析】【解答】
【分析】利用诱导公式结合两角和的正切公式求出的值。
8.
(2019?卷Ⅰ)已知非零向量,满足||=2|
|,且,则与的夹角为(
)
A.B.
C.
D.
【答案】B
【解析】【解答】
设与的夹角为
【分析】利用向量垂直数量积为0的等价关系,用数量积公式结合已知条件和两向量间夹角的取值范围求出与的夹角。
9.
(2019?卷Ⅰ)下图是求的程序框图,图中空白框中应填入(
)
A.A=
B.A=2+
C.A=
D.A=1+
【答案】A
【解析】【解答】
第一步:
第二步:
第三步:
因为输出的A的值满足题意输得的结果,所以判断框里应该填
【分析】利用已知条件结合程序框图的顺序结构、条件结构和循环结构求出满足要求的结果,从而确定判断框里所填的选项。
10.
(2019?卷Ⅰ)双曲线C:(a>0,b>0)的一条渐近线的倾斜角为130°,则C的离心率为(
)
A.2sin40°
B.2cos40°
C.
D.
【答案】D
【解析】【解答】
由双曲线的标准方程(a>0,b>0)得双曲线的一条渐近线方程为:
因为双曲线C:(a>0,b>0)的一条渐近线的倾斜角为130°,根据直线的斜率与直线的倾斜角的关系式,得:
利用同角三角函数基本关系式,得:
【分析】利用双曲线标准方程求出其一条渐近线方程,再利用直线的斜率与倾斜角的关系式找出与倾斜角的关系式,再利用双曲线中a,b,c三者的关系式结合双曲线中离心率公式变形,用同角三角函数的基本关系式化简求出双曲线的离心率。
11.
(2019?卷Ⅰ)?ABC的内角A,B,C的对边分别为a,b,c,已知asinA-bsinB=4csinC,cosA=,则=(
)
A.6
B.5
C.4
D.3
【答案】A
【解析】【解答】
由已知条件结合正弦定理,
①
利用余弦定理,得②
①②联立得:
【分析】利用已知条件结合正弦定理和余弦定理,变形得出b,c的关系式,从而求出的值。
12.
(2019?卷Ⅰ)已知椭圆C的焦点为F1(-1,0),F2(1,0)。过F2的直线与C交于A,B两点。若|AF1|=2|F2B|,|AB|=|BF1|,则C的方程为(
)
A.
+y2=1
B.
+=1
C.
+=1
D.
+=1
【答案】B
【解析】【解答】
如图,对角B用两次余弦定理,得:
得:
【分析】利用双曲线和三角形的图象的位置关系,结合双曲线的定义,对角B用两次余弦定理求出的值,从而求出双曲线的标准方程。
ニ、填空题;本题共4小题,每小题5分,共20分。
13.
(2019?卷Ⅰ)曲线在点处的切线方程为
.
【答案】
【解析】【解答】
设曲线y=3(x2+x)ex在点(0,0)处的切线方程为:
因为曲线y=3(x2+x)ex
,
【分析】利用求导的方法求出曲线在切点处的切线的斜率,再利用点斜式求出曲线y=3(x2+x)ex在点(0,0)处的切线方程。
14.
(2019?卷Ⅰ)记Sn为等比数列{an}的前n项和。若a1=,,则S4=
【答案】
【解析】【解答】
设等比数列的公比为q,利用等比数列的前n项和公式,
当时,
当时,
由求根公式求出q的值,根据题意,从而确定q的值。
【分析】利用分类讨论的方法结合等比数列前n项和公式求出q的值,从而利用与的关系式结合的值求出的值。
15.
(2019?卷Ⅰ)函数f(x)=sin(2x+)-3cosx的最小值为
.
【答案】-4
【解析】【解答】
利用诱导公式和二倍角的余弦公式得:利用换元法,令
当时,
【分析】利用诱导公式和二倍角的余弦公式化简将函数转化为二次函数,再利用二次函数求最值的方法求出函数的最小值。
16.
(2019?卷Ⅰ)已知ACB=90°,P为平面ABC外一点,PC=2,点P到ACB两边AC,BC的距离均为,那么P到平面ABC的距离为
。
【答案】
【解析】【解答】
设点P在平面ABC的距离为d,设点P在平面ABC投影点为O,所以d=PO,过点P作BC边的垂线,垂足为D,连接OP,OC,OD,则即为PC与平面ABC所成的平面角,因为点P到ACB两边AC,BC的距离均为,故点O在ACB的角平分线上,即由于PC=2,则三角形PCD在地底面上的投影三角形OCD为等腰直角三角形,
利用勾股定理得:
点P在平面ABC投影点为O,
所以三角形POC是直角三角形,利用勾股定理得:
【分析】利用投影原理结合线面垂直的定义证出线线垂直,再利用线线垂直满足勾股定理,用勾股定理求出点P在平面ABC的距离。
三、解答题:共70分。解答应写出文字说明,证明过程或演算步骤。第17~21题为必考题,每个试题考生都必须作答,第22、23题为选考题,考生根据要求作答。
17.
(2019?卷Ⅰ)某商场为提高服务质量,随机调查了50名男顾客和50名女顾客,每位顾客对该商场的服务给出满意或不满意的评价,得到下面列联表:
满意
不满意
男顾客
40
10
女顾客
30
20
(1)分别估计男、女顾客对该商场服务满意的概率;
【解析】【解答】
由调查数据,男顾客中对该商场服务满意的比率为,因此男顾客对该商场服务满意的概率的估计值为0.8,女顾客中对该商场服务满意的比率为,因此女顾客对该商场服务满意的概率的估计值为0.6。
(2)能否有95%的把握认为男、女顾客对该商场服务的评价有差异?
附:K2=
P(K2≧k)
0.050
0.010
0.001
k
3.841
6.635
10.828
【解析】【解答】
(2).
由于,故有95%的把握认为男、女顾客对该商场服务的评价有差异.
【分析】(1)根据实际问题的已知条件结合的列联表,用的公式估计出男、女顾客对该商场服务满意的概率。
(2)根据实际问题的已知条件结合的列联表,用独立性检验的方法判断出有95%的把握认为男、女顾客对该商场服务的评价有差异。
18.
(2019?卷Ⅰ)记Sn为等差数列{an}的前n项和,已知Sn=-a5
(1)若a3=4,求{an}的通项公式。
【解析】【解答】
(1)设的公差为d.
由得.
由a3=4得.
于是.
因此的通项公式为.
(2)若a1≥0,求使得Sn≥an的n取值范围。
【解析】【解答】
(2)由(1)得,故.
由知,故等价于,解得1≤n≤10.
所以n的取值范围是.
【分析】(1)利用等差数列的通项公式和等差数列的前n项和公式结合已知条件求出等差数列的首项和公差,从而求出等差数列的通项公式。
由(1)得,故.
由知,故等价于,再利用一元二次不等式求解集的方法结合n自身的取值范围,从而求出n的取值范围。
19.
(2019?卷Ⅰ)如图,直四棱柱ABCD-A1B1C1D1的底面是菱形,AA1=4,AB=2,BAD=60°,E,M,N分别是BC,BB1,A1D的中点
证明:MN∥平面C1DE;
【解析】【解答】
(1)连结.因为M,E分别为的中点,所以,且.又因为N为的中点,所以.
由题设知,可得,故,因此四边形MNDE为平行四边形,.又平面,所以MN∥平面.
求点C到平面C1DE的距离。
【解析】【解答】
(2)过C作C1E的垂线,垂足为H.
由已知可得,,所以DE⊥平面,故DE⊥CH.
从而CH⊥平面,故CH的长即为C到平面的距离,
由已知可得CE=1,C1C=4,所以,故.
从而点C到平面的距离为.
【分析】(1)利用直四棱柱的结构特征结合已知条件,用中点作中位线证线线平行,再利用线线相等结合平行四边形的定义证出四边形MNDE为平行四边形,再利用平行四边形的定义证出另一组线线平行,从而用线线平行结合线面平行的判定定理证出线面平行。
(2)利用直四棱柱的结构特征结合已知条件,用线面垂直的定义证出线线垂直,再利用线面垂直结合线面垂直的判定定理证出线面垂直,从而推出CH的长即为C到平面的距离,由已知可得CE=1,C1C=4,所以,故从而点C到平面的距离为.
20.
(2019?卷Ⅰ)已知函数f(x)=2sinx-xcosx-x,f‘(x)为f(x)的导数。
(1)证明:f(x)在区间(0,
π)存在唯一零点;
【解析】【解答】
(1)设,则.
当时,;当时,,所以在单调递增,在单调递减.又,故在存在唯一零点.
所以在存在唯一零点.
(2)若x?[0,π]时,f(x)≥ax,求a的取值范围。
【解析】【解答】
(2)由题设知,可得a≤0.
由(1)知,在只有一个零点,设为,且当时,;当时,,所以在单调递增,在单调递减.
又,所以,当时,.
又当时,ax≤0,故.
因此,a的取值范围是.
【分析】(1)利用求导的方法判断函数的单调性,再利用零点存在性定理证出函数在区间(0,
π)存在唯一零点。
(2)由题设知,可得a≤0.
由(1)知,在只有一个零点,
利用求导的方法判断函数的单调性,再利用零点存在性定理求出的取值范围。
21.
(2019?卷Ⅰ)已知点A,B关于坐标原点O对称,|AB|=4,⊙M过点A,B且与直线x+2=0相切。
(1)若A在直线x+y=0上,求⊙M的半径。
【解析】【解答】
因为过点,所以圆心M在AB的垂直平分线上.由已知A在直线上,
且关于坐标原点O对称,所以M在直线上,故可设.
因为与直线x+2=0相切,所以的半径为.
由已知得,又,故可得,解得或.
故的半径或.
(2)是否存在定点P,使得当A运动时,|MA|-|MP|为定值?并说明理由。
【解析】【解答】
(2)存在定点,使得为定值.
理由如下:
设,由已知得的半径为.
由于,故可得,化简得M的轨迹方程为.
因为曲线是以点为焦点,以直线为准线的抛物线,
所以因为,所以存在满足条件的定点P。
【分析】(1)因为过点,利用垂直平分线的性质推出圆心M在AB的垂直平分线上,再由点A在直线上,结合点与点关于点对称的性质和求解方法推出点M在直线上,故可设,再利用直线与圆相切的位置关系的判断方法求出的半径与的关系式,再由已知得,结合两向量垂直,用勾股定理求出的值,从而求出的半径。
(2)设,由已知得的半径为
再由两向量垂直,用勾股定理求出点M的轨迹方程,从而判断出点M的轨迹为抛物线,因为曲线是以点为焦点,以直线为准线的抛物线,再利用抛物线的定义得出因为,所以存在满足条件的定点使得为定值。
四、选考题,共10分。请考生在第22、23题中任选一直作答。如果多做。则按所做的第一题计分。
22.
(2019?卷Ⅰ)在直角坐标系xOy中,曲线C的参数方程为(t为参数)。以坐标原点O为极点,x轴的正半轴为极轴建立极坐标系,直线l的极坐标方程为2ρcosθ+ρsinθ+11=0。
(1)求C和l的直角坐标方程;
【解析】【解答】
因为,且,
所以C的直角坐标方程为.
.
(2)求C上的点到l距离的最小值。
【解析】【解答】
(2)由(1)可设曲线C的参数方程为(为参数,).
曲线C上的点到的距离为.
当时,取得最小值7,故C上的点到距离的最小值为.
【分析】(1)利用参数方程转化为直角坐标方程的方法结合极坐标与直角坐标的互化公式求出曲线C和直线的直角坐标方程。
(2)利用参数表示满足曲线C上的点的坐标,再利用点到直线的距离公式结合辅助角公式化简转化为三角型函数,再利用还原法将三角型函数转化为余弦函数,再利用余弦函数的图象求出三角型函数的最小值,从而求出曲线C上的点到直线的距离的最小值。
23.
(2019?卷Ⅰ)已知a,b,c为正数,且满足abc=1。证明:
(1);
【解析】【解答】
(1)因为,又,故有
.
所以.
(2)(a+b)3+(b+c)3+(c+a)3≥24。
【解析】【解答】
(2)因为为正数且,故有
=24.
所以.
【分析】(1)利用均值不等式求最值的方法结合已知条件变形证出不等式成立。
(2)利用均值不等式求最值的方法结合已知条件变形证出不等式成立。
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)
同课章节目录
