2019年高考数学真题分类汇编专题14:三角函数(综合题)
文档属性
| 名称 | 2019年高考数学真题分类汇编专题14:三角函数(综合题) |  | |
| 格式 | rar | ||
| 文件大小 | 315.2KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-06-14 16:16:21 | ||
图片预览




文档简介
2019年高考数学真题分类汇编专题14:三角函数(综合题)
一、解答题
1.(2019?江苏)在△ABC中,角A , B , C的对边分别为a , b , c .
(1)若a=3c , b= ,cosB= ,求c的值;
(2)若 ,求 的值.
2.[选修4-4:坐标系与参数方程]在极坐标系中,已知两点 ,直线l的方程为 .
(1)求A , B两点间的距离;
(2)求点B到直线l的距离.
3.(2019?江苏)如图,一个湖的边界是圆心为O的圆,湖的一侧有一条直线型公路l , 湖上有桥AB(AB是圆O的直径).规划在公路l上选两个点P、Q , 并修建两段直线型道路PB、QA . 规划要求:线段PB、QA上的所有点到点O的距离均不小于圆O的半径.已知点A、B到直线l的距离分别为AC和BD(C、D为垂足),测得AB=10,AC=6,BD=12(单位:百米).
(1)若道路PB与桥AB垂直,求道路PB的长;
(2)在规划要求下,P和Q中能否有一个点选在D处?并说明理由;
(3)对规划要求下,若道路PB和QA的长度均为d(单位:百米).求当d最小时,P、Q两点间的距离.
4.(2019?浙江)设函数f(x)=sinx,x R。
(1)已知θ=[0,2x),函数f(x+θ)是偶函数,求θ的值
(2)求函数y=[f(x)+ ]2+[f(x+ )]2的值域
5.(2019?天津)在 中,内角 所对的边分别为 .已知 , .
(Ⅰ)求 的值;
(Ⅱ)求 的值.
6.(2019?全国Ⅲ)△ABC的内角A、B、C的对边分别为a,b,c,已知
(1)求B;
(2)若△ABC为锐角三角形,且c=1,求△ABC面积的取值范围.
7.(2019?北京)在△ABC中,a=3,b-c=2,cosB=- .
(I)求b,c的值:
(II)求sin(B+C)的值.
8.(2019?北京)在△ABC中,a=3,b-c=2,cosB=- .
(I)求b,c的值;
(II)求sin(B-C)的值.
9.(2019?卷Ⅰ)?ABC的内角A,B,C的对边分别为a,b,c.设(sinB-sinC)2=sin2A-sinBsinC。
(1)求A;
(2)若 ,求sinC.
答案解析部分
一、解答题
1.【答案】 (1)解:因为 ,
由余弦定理 ,得 ,即 .
所以 (2)解:因为 ,
由正弦定理 ,得 ,所以 .
从而 ,即 ,故 .
因为 ,所以 ,从而 .
因此
【考点】正弦定理,余弦定理
【解析】【分析】(1)根据已知条件结合余弦定理求出c的值。 (2)根据已知条件结合正弦定理得出 ,再利用同角三角函数基本关系式和诱导公式求出 的值。
2.【答案】 (1)解:设极点为O.在△OAB中,A(3, ),B( , ),
由余弦定理,得AB=
(2)解:因为直线l的方程为 ,
则直线l过点 ,倾斜角为 .
又 ,所以点B到直线l的距离为
【考点】余弦定理的应用,极坐标刻画点的位置
【解析】【分析】(1)利用极坐标与直角坐标的互化公式结合余弦定理求出A,B两点间的距离。(2)利用直线l过点 ,倾斜角为 ,再利用直线的倾斜角和直线斜率的关系式求出直线斜率,从而用点斜式求出直线方程,再利用点到直线的距离公式求出点B到直线l的距离.
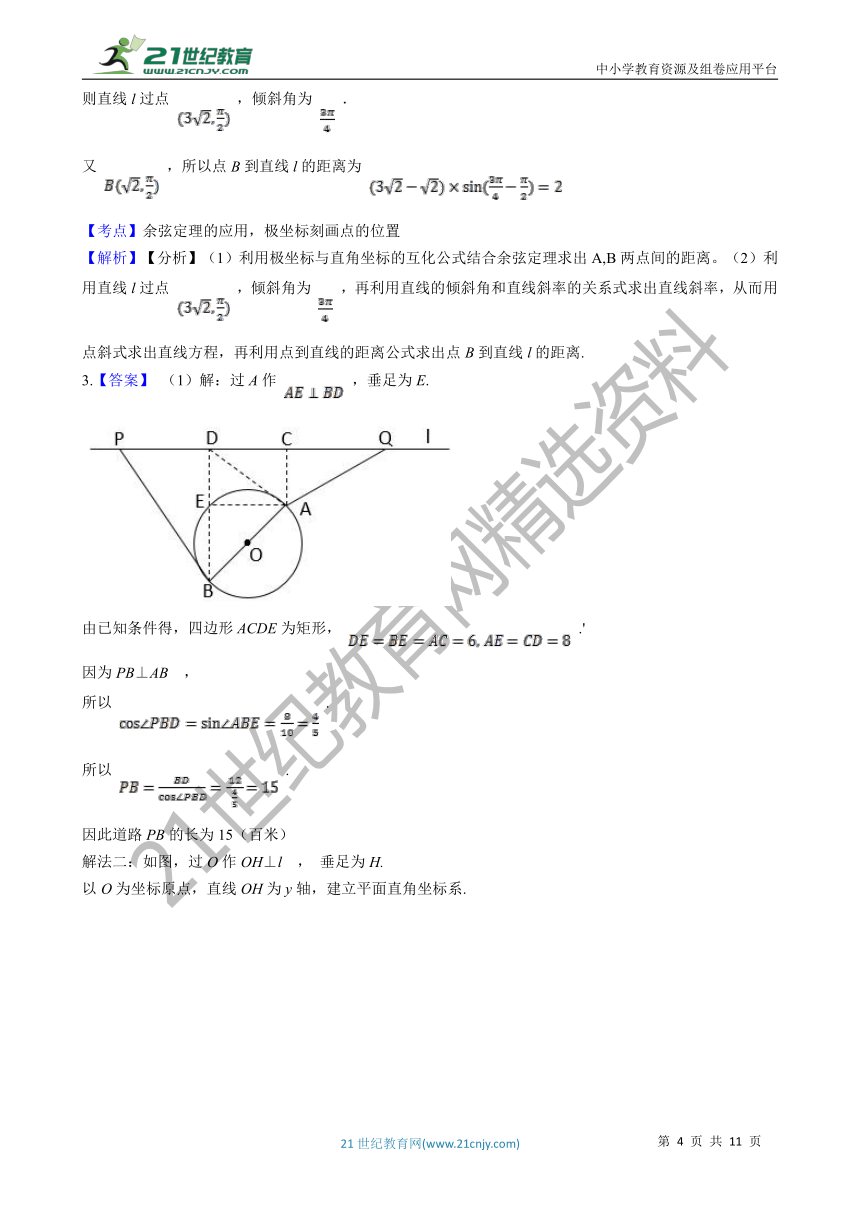
3.【答案】 (1)解:过A作 ,垂足为E.
由已知条件得,四边形ACDE为矩形, .'
因为PB⊥AB ,
所以 .
所以 .
因此道路PB的长为15(百米)
解法二:如图,过O作OH⊥l , 垂足为H. 以O为坐标原点,直线OH为y轴,建立平面直角坐标系.
因为BD=12,AC=6,所以OH=9,直线l的方程为y=9,点A , B的纵坐标分别为3,?3.
因为AB为圆O的直径,AB=10,所以圆O的方程为x2+y2=25.
从而A(4,3),B(?4,?3),直线AB的斜率为 .
因为PB⊥AB , 所以直线PB的斜率为 ,
直线PB的方程为 .
所以P(?13,9), .
因此道路PB的长为15(百米)
(2)解:①若P在D处,由(1)可得E在圆上,则线段BE上的点(除B , E)到点O的距离均小于圆O的半径,所以P选在D处不满足规划要求.
②若Q在D处,连结AD , 由(1)知 ,
从而 ,所以∠BAD为锐角.
所以线段AD上存在点到点O的距离小于圆O的半径.
因此,Q选在D处也不满足规划要求.
综上,P和Q均不能选在D处.
解法二:①若P在D处,取线段BD上一点E(?4,0),则EO=4<5,所以P选在D处不满足规划要求.
②若Q在D处,连结AD , 由(1)知D(?4,9),又A(4,3),
所以线段AD: .
在线段AD上取点M(3, ),因为 ,
所以线段AD上存在点到点O的距离小于圆O的半径.
因此Q选在D处也不满足规划要求.
综上,P和Q均不能选在D处.
(3)解:先讨论点P的位置.
当∠OBP<90°时,线段PB上存在点到点O的距离小于圆O的半径,点P不符合规划要求;
当∠OBP≥90°时,对线段PB上任意一点F , OF≥OB , 即线段PB上所有点到点O的距离均不小于圆O的半径,点P符合规划要求.
设 为l上一点,且 ,由(1)知, B=15,
此时 ;
当∠OBP>90°时,在 中, .
由上可知,d≥15.
再讨论点Q的位置.
由(2)知,要使得QA≥15,点Q只有位于点C的右侧,才能符合规划要求.当QA=15时, .此时,线段QA上所有点到点O的距离均不小于圆O的半径.
综上,当PB⊥AB , 点Q位于点C右侧,且CQ= 时,d最小,此时P , Q两点间的距离PQ=PD+CD+CQ=17+ .
因此,d最小时,P , Q两点间的距离为17+ (百米)
解法二:先讨论点P的位置.
当∠OBP<90°时,线段PB上存在点到点O的距离小于圆O的半径,点P不符合规划要求;
当∠OBP≥90°时,对线段PB上任意一点F , OF≥OB , 即线段PB上所有点到点O的距离均不小于圆O的半径,点P符合规划要求.
设 为l上一点,且 ,由(1)知, B=15,此时 (?13,9);
当∠OBP>90°时,在 中, .
由上可知,d≥15.
再讨论点Q的位置.
由(2)知,要使得QA≥15,点Q只有位于点C的右侧,才能符合规划要求.当QA=15时,设Q(a , 9),由 ,得a= ,所以Q( ,9),此时,线段QA上所有点到点O的距离均不小于圆O的半径.
综上,当P(?13,9),Q( ,9)时,d最小,此时P , Q两点间的距离
.
因此,d最小时,P , Q两点间的距离为 (百米)
【考点】余弦定理的应用,三角形中的几何计算,解三角形的实际应用
【解析】【分析】(1)利用两种方法求出道路PB的长,第一种方法是利用矩形的性质结合直角三角形中正余弦值的关系式求出道路PB的长;第二种方法利用建系的方法结合直线和直线垂直求出未知直线的斜率,再利用直线与圆的位置关系求出所求直线的方程,再利用两点距离公式求出道路PB的长。(2)利用两种方法得出P和Q均不能选在D处,第一种方法利用实际问题的已知条件结合余弦定理得出P和Q均不能选在D处;第二种方法利用实际问题的已知条件结合两点距离公式得出P和Q均不能选在D处。(3)利用两种方法得出当d最小时,P , Q两点间的距离为17+ (百米),第一种方法是利用分类讨论的方法结合讨论P,Q的位置,用勾股定理结合几何方法求出当PB⊥AB , 点Q位于点C右侧,且CQ= 时,d最小,从而求出P , Q两点间的距离为17+ (百米);第二种方法是利用分类讨论的方法结合讨论P,Q的位置,用两点距离公式结合线段QA上所有点到点O的距离均不小于圆O的半径.,得出当d最小时,P , Q两点间的距离为17+ (百米)。
4.【答案】 (1)因为 是偶函数,所以,对任意实数x都有 ,
即 ,
故 ,
所以 .
又 ,因此 或 .
(2)
.
因此,函数的值域是 .
【考点】正弦函数的奇偶性,正弦函数的定义域和值域
【解析】【分析】(1)根据函数的奇偶性求出余弦值,即可确定角的大小; (2)根据余弦的二倍角公式,结合辅助角公式及余弦函数的有界性,即可求出函数的值域.
5.【答案】 解:在 中,由正弦定理 ,得 ,又由 ,得 ,即 .又因为 ,得到 , .由余弦定理可得 .
(Ⅱ)由(Ⅰ)可得 ,从而 , ,故
【考点】三角函数的恒等变换及化简求值,正弦定理,余弦定理
【解析】【分析】(Ⅰ)利用正余弦定理即可求得
(Ⅱ)利用 ,求得 ,进而根据二倍角公式求出 , ,再利用两角和的正弦即可求得答案。
本题考查同角三角函数的基本关系式、两角和的公式、倍角公式、正余弦定理等知识。
6.【答案】 (1)解:由题设及正弦定理得 .
因为sinA 0,所以 .
由 ,可得 ,故 .
因为 ,故 ,因此B=60°. (2)由题设及(1)知△ABC的面积 .
由正弦定理得 .
由于△ABC为锐角三角形,故0°因此,△ABC面积的取值范围是 .
【考点】正弦定理的应用,三角形中的几何计算
【解析】【分析】(1)由已知利用正弦定理列式,结合诱导公式化简,即可求出角B的值;(2)利用正弦定理列式,结合△ABC为锐角三角形得到 ,即可求出△ABC面积的取值范围.
7.【答案】 解:(I)根据余弦定理 ,
故 ,
解得c=5,B=7;
(II)根据 ,得 ,
根据正弦定理, ,
得 ,解得 ,所以 ,
所以 .
【考点】两角和与差的正弦函数,正弦定理,余弦定理
【解析】【分析】(I)根据余弦定理,解方程即可求出c和b;
(II)根据同角三角函数的平方关系,求出sinB,结合正弦定理,求出sinC和cosC,即可依据两角和的正弦公式,求出sin(B+C).
8.【答案】 解:(I)根据余弦定理 ,
故 ,
解得c=5,B=7;
(II)根据 ,得 ,
根据正弦定理, ,
得 ,解得 ,所以 ,
所以 .
【考点】两角和与差的正弦函数,正弦定理,余弦定理
【解析】【分析】(I)根据余弦定理,解方程即可求出c和b;
(II)根据同角三角函数的平方关系,求出sinB,结合正弦定理,求出sinC和cosC,即可依据两角和的正弦公式,求出sin(B-C).
9.【答案】 (1)解:
由正弦定理得:
由余弦定理得:
在三角形中,
(2)解: 由正弦定理得:
代入A得:
【考点】正弦定理,三角形中的几何计算
【解析】【分析】(1)利用实际问题的已知条件结合正弦定理和余弦定理求出角A的余弦值。(2)利用实际问题的已知条件结合正弦定理和辅助角公式求出 从而求出角C的值,再利用两角和的正弦公式求出角C的正弦值.
一、解答题
1.(2019?江苏)在△ABC中,角A , B , C的对边分别为a , b , c .
(1)若a=3c , b= ,cosB= ,求c的值;
(2)若 ,求 的值.
2.[选修4-4:坐标系与参数方程]在极坐标系中,已知两点 ,直线l的方程为 .
(1)求A , B两点间的距离;
(2)求点B到直线l的距离.
3.(2019?江苏)如图,一个湖的边界是圆心为O的圆,湖的一侧有一条直线型公路l , 湖上有桥AB(AB是圆O的直径).规划在公路l上选两个点P、Q , 并修建两段直线型道路PB、QA . 规划要求:线段PB、QA上的所有点到点O的距离均不小于圆O的半径.已知点A、B到直线l的距离分别为AC和BD(C、D为垂足),测得AB=10,AC=6,BD=12(单位:百米).
(1)若道路PB与桥AB垂直,求道路PB的长;
(2)在规划要求下,P和Q中能否有一个点选在D处?并说明理由;
(3)对规划要求下,若道路PB和QA的长度均为d(单位:百米).求当d最小时,P、Q两点间的距离.
4.(2019?浙江)设函数f(x)=sinx,x R。
(1)已知θ=[0,2x),函数f(x+θ)是偶函数,求θ的值
(2)求函数y=[f(x)+ ]2+[f(x+ )]2的值域
5.(2019?天津)在 中,内角 所对的边分别为 .已知 , .
(Ⅰ)求 的值;
(Ⅱ)求 的值.
6.(2019?全国Ⅲ)△ABC的内角A、B、C的对边分别为a,b,c,已知
(1)求B;
(2)若△ABC为锐角三角形,且c=1,求△ABC面积的取值范围.
7.(2019?北京)在△ABC中,a=3,b-c=2,cosB=- .
(I)求b,c的值:
(II)求sin(B+C)的值.
8.(2019?北京)在△ABC中,a=3,b-c=2,cosB=- .
(I)求b,c的值;
(II)求sin(B-C)的值.
9.(2019?卷Ⅰ)?ABC的内角A,B,C的对边分别为a,b,c.设(sinB-sinC)2=sin2A-sinBsinC。
(1)求A;
(2)若 ,求sinC.
答案解析部分
一、解答题
1.【答案】 (1)解:因为 ,
由余弦定理 ,得 ,即 .
所以 (2)解:因为 ,
由正弦定理 ,得 ,所以 .
从而 ,即 ,故 .
因为 ,所以 ,从而 .
因此
【考点】正弦定理,余弦定理
【解析】【分析】(1)根据已知条件结合余弦定理求出c的值。 (2)根据已知条件结合正弦定理得出 ,再利用同角三角函数基本关系式和诱导公式求出 的值。
2.【答案】 (1)解:设极点为O.在△OAB中,A(3, ),B( , ),
由余弦定理,得AB=
(2)解:因为直线l的方程为 ,
则直线l过点 ,倾斜角为 .
又 ,所以点B到直线l的距离为
【考点】余弦定理的应用,极坐标刻画点的位置
【解析】【分析】(1)利用极坐标与直角坐标的互化公式结合余弦定理求出A,B两点间的距离。(2)利用直线l过点 ,倾斜角为 ,再利用直线的倾斜角和直线斜率的关系式求出直线斜率,从而用点斜式求出直线方程,再利用点到直线的距离公式求出点B到直线l的距离.
3.【答案】 (1)解:过A作 ,垂足为E.
由已知条件得,四边形ACDE为矩形, .'
因为PB⊥AB ,
所以 .
所以 .
因此道路PB的长为15(百米)
解法二:如图,过O作OH⊥l , 垂足为H. 以O为坐标原点,直线OH为y轴,建立平面直角坐标系.
因为BD=12,AC=6,所以OH=9,直线l的方程为y=9,点A , B的纵坐标分别为3,?3.
因为AB为圆O的直径,AB=10,所以圆O的方程为x2+y2=25.
从而A(4,3),B(?4,?3),直线AB的斜率为 .
因为PB⊥AB , 所以直线PB的斜率为 ,
直线PB的方程为 .
所以P(?13,9), .
因此道路PB的长为15(百米)
(2)解:①若P在D处,由(1)可得E在圆上,则线段BE上的点(除B , E)到点O的距离均小于圆O的半径,所以P选在D处不满足规划要求.
②若Q在D处,连结AD , 由(1)知 ,
从而 ,所以∠BAD为锐角.
所以线段AD上存在点到点O的距离小于圆O的半径.
因此,Q选在D处也不满足规划要求.
综上,P和Q均不能选在D处.
解法二:①若P在D处,取线段BD上一点E(?4,0),则EO=4<5,所以P选在D处不满足规划要求.
②若Q在D处,连结AD , 由(1)知D(?4,9),又A(4,3),
所以线段AD: .
在线段AD上取点M(3, ),因为 ,
所以线段AD上存在点到点O的距离小于圆O的半径.
因此Q选在D处也不满足规划要求.
综上,P和Q均不能选在D处.
(3)解:先讨论点P的位置.
当∠OBP<90°时,线段PB上存在点到点O的距离小于圆O的半径,点P不符合规划要求;
当∠OBP≥90°时,对线段PB上任意一点F , OF≥OB , 即线段PB上所有点到点O的距离均不小于圆O的半径,点P符合规划要求.
设 为l上一点,且 ,由(1)知, B=15,
此时 ;
当∠OBP>90°时,在 中, .
由上可知,d≥15.
再讨论点Q的位置.
由(2)知,要使得QA≥15,点Q只有位于点C的右侧,才能符合规划要求.当QA=15时, .此时,线段QA上所有点到点O的距离均不小于圆O的半径.
综上,当PB⊥AB , 点Q位于点C右侧,且CQ= 时,d最小,此时P , Q两点间的距离PQ=PD+CD+CQ=17+ .
因此,d最小时,P , Q两点间的距离为17+ (百米)
解法二:先讨论点P的位置.
当∠OBP<90°时,线段PB上存在点到点O的距离小于圆O的半径,点P不符合规划要求;
当∠OBP≥90°时,对线段PB上任意一点F , OF≥OB , 即线段PB上所有点到点O的距离均不小于圆O的半径,点P符合规划要求.
设 为l上一点,且 ,由(1)知, B=15,此时 (?13,9);
当∠OBP>90°时,在 中, .
由上可知,d≥15.
再讨论点Q的位置.
由(2)知,要使得QA≥15,点Q只有位于点C的右侧,才能符合规划要求.当QA=15时,设Q(a , 9),由 ,得a= ,所以Q( ,9),此时,线段QA上所有点到点O的距离均不小于圆O的半径.
综上,当P(?13,9),Q( ,9)时,d最小,此时P , Q两点间的距离
.
因此,d最小时,P , Q两点间的距离为 (百米)
【考点】余弦定理的应用,三角形中的几何计算,解三角形的实际应用
【解析】【分析】(1)利用两种方法求出道路PB的长,第一种方法是利用矩形的性质结合直角三角形中正余弦值的关系式求出道路PB的长;第二种方法利用建系的方法结合直线和直线垂直求出未知直线的斜率,再利用直线与圆的位置关系求出所求直线的方程,再利用两点距离公式求出道路PB的长。(2)利用两种方法得出P和Q均不能选在D处,第一种方法利用实际问题的已知条件结合余弦定理得出P和Q均不能选在D处;第二种方法利用实际问题的已知条件结合两点距离公式得出P和Q均不能选在D处。(3)利用两种方法得出当d最小时,P , Q两点间的距离为17+ (百米),第一种方法是利用分类讨论的方法结合讨论P,Q的位置,用勾股定理结合几何方法求出当PB⊥AB , 点Q位于点C右侧,且CQ= 时,d最小,从而求出P , Q两点间的距离为17+ (百米);第二种方法是利用分类讨论的方法结合讨论P,Q的位置,用两点距离公式结合线段QA上所有点到点O的距离均不小于圆O的半径.,得出当d最小时,P , Q两点间的距离为17+ (百米)。
4.【答案】 (1)因为 是偶函数,所以,对任意实数x都有 ,
即 ,
故 ,
所以 .
又 ,因此 或 .
(2)
.
因此,函数的值域是 .
【考点】正弦函数的奇偶性,正弦函数的定义域和值域
【解析】【分析】(1)根据函数的奇偶性求出余弦值,即可确定角的大小; (2)根据余弦的二倍角公式,结合辅助角公式及余弦函数的有界性,即可求出函数的值域.
5.【答案】 解:在 中,由正弦定理 ,得 ,又由 ,得 ,即 .又因为 ,得到 , .由余弦定理可得 .
(Ⅱ)由(Ⅰ)可得 ,从而 , ,故
【考点】三角函数的恒等变换及化简求值,正弦定理,余弦定理
【解析】【分析】(Ⅰ)利用正余弦定理即可求得
(Ⅱ)利用 ,求得 ,进而根据二倍角公式求出 , ,再利用两角和的正弦即可求得答案。
本题考查同角三角函数的基本关系式、两角和的公式、倍角公式、正余弦定理等知识。
6.【答案】 (1)解:由题设及正弦定理得 .
因为sinA 0,所以 .
由 ,可得 ,故 .
因为 ,故 ,因此B=60°. (2)由题设及(1)知△ABC的面积 .
由正弦定理得 .
由于△ABC为锐角三角形,故0°
【考点】正弦定理的应用,三角形中的几何计算
【解析】【分析】(1)由已知利用正弦定理列式,结合诱导公式化简,即可求出角B的值;(2)利用正弦定理列式,结合△ABC为锐角三角形得到 ,即可求出△ABC面积的取值范围.
7.【答案】 解:(I)根据余弦定理 ,
故 ,
解得c=5,B=7;
(II)根据 ,得 ,
根据正弦定理, ,
得 ,解得 ,所以 ,
所以 .
【考点】两角和与差的正弦函数,正弦定理,余弦定理
【解析】【分析】(I)根据余弦定理,解方程即可求出c和b;
(II)根据同角三角函数的平方关系,求出sinB,结合正弦定理,求出sinC和cosC,即可依据两角和的正弦公式,求出sin(B+C).
8.【答案】 解:(I)根据余弦定理 ,
故 ,
解得c=5,B=7;
(II)根据 ,得 ,
根据正弦定理, ,
得 ,解得 ,所以 ,
所以 .
【考点】两角和与差的正弦函数,正弦定理,余弦定理
【解析】【分析】(I)根据余弦定理,解方程即可求出c和b;
(II)根据同角三角函数的平方关系,求出sinB,结合正弦定理,求出sinC和cosC,即可依据两角和的正弦公式,求出sin(B-C).
9.【答案】 (1)解:
由正弦定理得:
由余弦定理得:
在三角形中,
(2)解: 由正弦定理得:
代入A得:
【考点】正弦定理,三角形中的几何计算
【解析】【分析】(1)利用实际问题的已知条件结合正弦定理和余弦定理求出角A的余弦值。(2)利用实际问题的已知条件结合正弦定理和辅助角公式求出 从而求出角C的值,再利用两角和的正弦公式求出角C的正弦值.
同课章节目录
