2019年高考数学真题分类汇编专题04:数列(基础题)
文档属性
| 名称 | 2019年高考数学真题分类汇编专题04:数列(基础题) |  | |
| 格式 | zip | ||
| 文件大小 | 272.2KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-06-14 16:01:55 | ||
图片预览

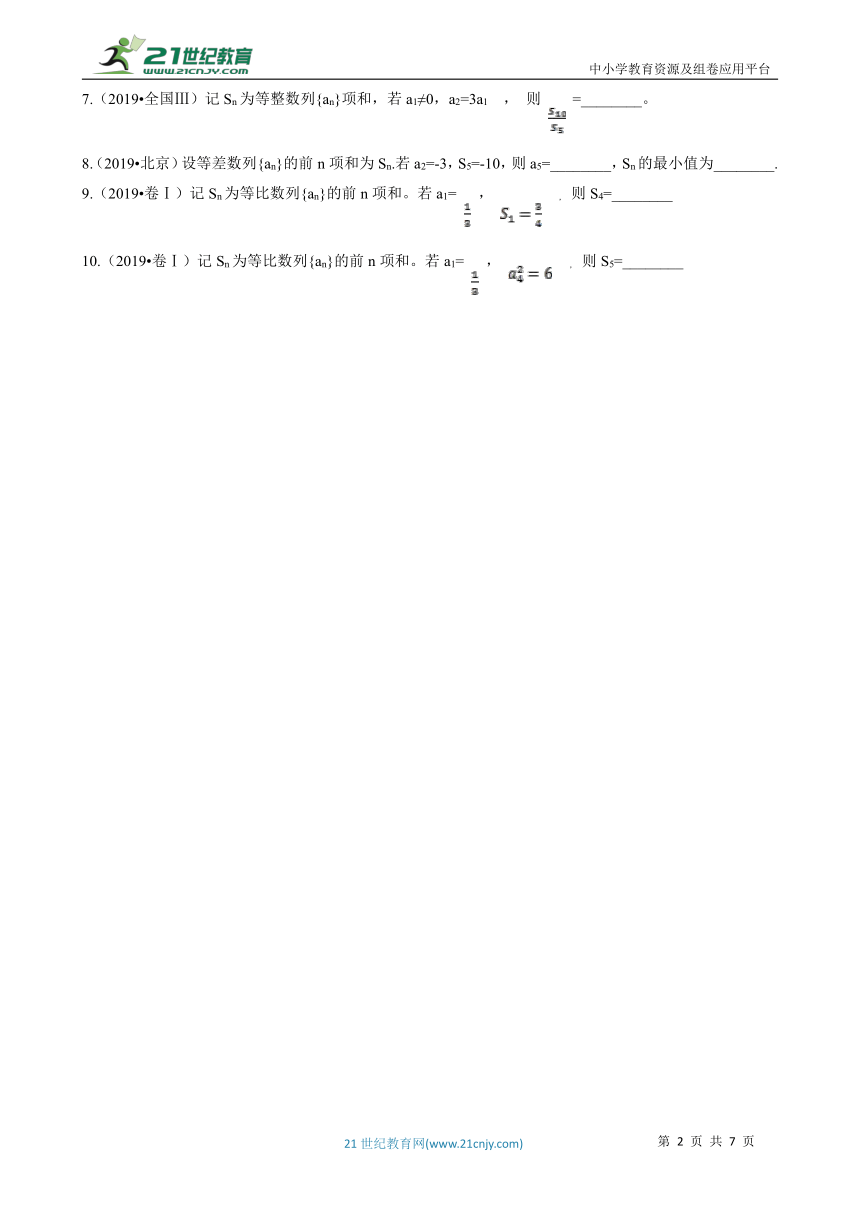

文档简介
2019年高考数学真题分类汇编专题04:数列(基础题)
一、单选题
1.(2019?浙江)设a,b∈R , 数列{an},满足an =a,an+1= an2+b,b∈N* , 则( ??)
A.?当b= 时,a10>10?????????????????????????????????????????B.?当b= 时,a10>10 C.?当b=-2时,a10>10????????????????????????????????????????????D.?当b=-4时,a10>10
2.(2019?全国Ⅲ)已知各项均为正数的等比数列{an}的前4项和为15,且a5=3a3+4a1 , 则a3=( ??)
A.?16???????????????????????????????????????????B.?8???????????????????????????????????????????C.?4???????????????????????????????????????????D.?2
3.(2019?卷Ⅰ)古希腊吋期,人们认为最美人体的头顶至肚脐的长度与肚脐至足底的长度之比是 ,称为黄金分割比例),著名的“断臂维纳斯“便是如此。此外,最美人体的头顶至咽喉的长度与咽喉至肚脐的长度也是 。若某人满足上述两个黄金分割比例,且腿长为105cm,头顶至脖子下端的长度为26cm,则其身高可能是(?? )
A.?165cm???????????????????????????????B.?175cm???????????????????????????????C.?185cm???????????????????????????????D.?190cm
4.(2019?卷Ⅰ)记Sn为等差数列 的前n项和。已知 =0, =5,则(?? )
A.?an=2n-5?????????????????????? ?B.?an=3n-10????????????????? ??????C.?Sn=2n2-8n???????????????????????D.?Sn= n2-2n
二、填空题
5.(2019?江苏)已知数列 是等差数列, 是其前n项和.若 ,则 的值是________.
6.(2019?全国Ⅲ)记Sn为等差数列{an}的前n项和,若 ,则 ________.
7.(2019?全国Ⅲ)记Sn为等整数列{an}项和,若a1≠0,a2=3a1 , 则 =________。
8.(2019?北京)设等差数列{an}的前n项和为Sn.若a2=-3,S5=-10,则a5=________,Sn的最小值为________.
9.(2019?卷Ⅰ)记Sn为等比数列{an}的前n项和。若a1= , , 则S4=________
10.(2019?卷Ⅰ)记Sn为等比数列{an}的前n项和。若a1= , , 则S5=________
答案解析部分
一、单选题
1.【答案】 A
【考点】数列的函数特性
【解析】【解答】选项B:不动点满足 时,如图,若 ,
排除
如图,若 为不动点 则
选项C:不动点满足 ,不动点为 ,令 ,则 ,
排除
选项D:不动点满足 ,不动点为 ,令 ,则 ,排除.
故答案为:A
【分析】遇到此类问题,可以利用函数方程思想,通过研究函数的不动点,进一步讨论 的可能取值,利用“排除法”求解.
2.【答案】 C
【考点】等比数列的通项公式
【解析】【解答】解:∵a5=3a3+4a1 , 则 ,∵ ,∴ ,
解得 或 (舍),∵各项均为正数,∴ ,又∵等比数列{an}的前4项为和为15,
∴ ,解得 ,∴ ,
故答案为:C.
【分析】由已知利用等比数列的通项公式列式,得到q=2,再由前4项为和为15列式,解得 ,即可求出 的值.
3.【答案】 B
【考点】等比数列的性质
【解析】【解答】因为头顶至肚脐的长度与肚脐至足底的长度之比是 ,成为黄金分割比例),此外,头顶至咽喉的长度与咽喉至肚脐的长度也是 ,所以设咽喉到肚脐的长度为 厘米,肚脐到腰的长度为 厘米,依题意得:
所以身高为 所以最接近的身高是175厘米。
故答案为:B
【分析】利用黄金比例的概念结合对应边成比例求出某人满足要求最接近的身高。
4.【答案】 A
【考点】等差数列
【解析】【解答】 利用等差数列通项公式和等差数列前n项和公式得,
①
②
①②联立求出:
故答案为:A
【分析】利用等差数列通项公式和等差数列前n项和公式结合已知条件求出等差数列的首项和公差,从而求出等差数列的通项公式。
二、填空题
5.【答案】 16
【考点】等差数列的前n项和
【解析】【解答】 数列 是等差数列,又
利用等差数列通项公式 得:
①
是等差数列 前n项和,且
利用等差数列前n项和公式 得:
②
①②联立,得:
【分析】根据已知条件结合等差数列通项公式和等差数列前n项和公式求出等差数列的首项和公差,再利用等差数列前n项和公式求出等差数列前8项的和。
6.【答案】 100
【考点】等差数列的前n项和
【解析】【解答】解:∵ ,∴ ,∴ ,
∴ ,
故答案为:100.
【分析】由已知列式 ,得到 ,代入等差数列的求和公式即可求值.
7.【答案】 4
【考点】等差数列的前n项和
【解析】【解答】解:∵等差数列{an}中 ,∴ ,∴ ,
故答案为:4.
【分析】由已知得到 ,利用等差数列的求和公式,代入化简即可求值.
8.【答案】 0 ;-10
【考点】等差数列
【解析】【解答】解: ,
解得 ,所以 ,
,
根据二次函数的性质,当n=4或5时, 有最小值-10.
故答案为:0;-10.
【分析】根据等差数列的通项公式和前n项和公式,解方程组求出首项和公差,即可求出 和 ,结合二次函数的性质求出最小值即可.
9.【答案】
【考点】等比数列
【解析】【解答】设等比数列的公比为q,利用等比数列的前n项和公式,
当 时,
当 时,
由求根公式求出q的值,根据题意, 从而确定q的值。
【分析】利用分类讨论的方法结合等比数列前n项和公式求出q的值,从而利用 与 的关系式结合 的值求出 的值。
10.【答案】
【考点】等比数列
【解析】【解答】 利用等比数列通项公式得,
①
②
①②联立求出:
【分析】利用等比数列通项公式和等比数列前n项和公式结合已知条件 求出等比数列的公比,从而利用等比数列的首项和公比求出等比数列的前5项的和。
一、单选题
1.(2019?浙江)设a,b∈R , 数列{an},满足an =a,an+1= an2+b,b∈N* , 则( ??)
A.?当b= 时,a10>10?????????????????????????????????????????B.?当b= 时,a10>10 C.?当b=-2时,a10>10????????????????????????????????????????????D.?当b=-4时,a10>10
2.(2019?全国Ⅲ)已知各项均为正数的等比数列{an}的前4项和为15,且a5=3a3+4a1 , 则a3=( ??)
A.?16???????????????????????????????????????????B.?8???????????????????????????????????????????C.?4???????????????????????????????????????????D.?2
3.(2019?卷Ⅰ)古希腊吋期,人们认为最美人体的头顶至肚脐的长度与肚脐至足底的长度之比是 ,称为黄金分割比例),著名的“断臂维纳斯“便是如此。此外,最美人体的头顶至咽喉的长度与咽喉至肚脐的长度也是 。若某人满足上述两个黄金分割比例,且腿长为105cm,头顶至脖子下端的长度为26cm,则其身高可能是(?? )
A.?165cm???????????????????????????????B.?175cm???????????????????????????????C.?185cm???????????????????????????????D.?190cm
4.(2019?卷Ⅰ)记Sn为等差数列 的前n项和。已知 =0, =5,则(?? )
A.?an=2n-5?????????????????????? ?B.?an=3n-10????????????????? ??????C.?Sn=2n2-8n???????????????????????D.?Sn= n2-2n
二、填空题
5.(2019?江苏)已知数列 是等差数列, 是其前n项和.若 ,则 的值是________.
6.(2019?全国Ⅲ)记Sn为等差数列{an}的前n项和,若 ,则 ________.
7.(2019?全国Ⅲ)记Sn为等整数列{an}项和,若a1≠0,a2=3a1 , 则 =________。
8.(2019?北京)设等差数列{an}的前n项和为Sn.若a2=-3,S5=-10,则a5=________,Sn的最小值为________.
9.(2019?卷Ⅰ)记Sn为等比数列{an}的前n项和。若a1= , , 则S4=________
10.(2019?卷Ⅰ)记Sn为等比数列{an}的前n项和。若a1= , , 则S5=________
答案解析部分
一、单选题
1.【答案】 A
【考点】数列的函数特性
【解析】【解答】选项B:不动点满足 时,如图,若 ,
排除
如图,若 为不动点 则
选项C:不动点满足 ,不动点为 ,令 ,则 ,
排除
选项D:不动点满足 ,不动点为 ,令 ,则 ,排除.
故答案为:A
【分析】遇到此类问题,可以利用函数方程思想,通过研究函数的不动点,进一步讨论 的可能取值,利用“排除法”求解.
2.【答案】 C
【考点】等比数列的通项公式
【解析】【解答】解:∵a5=3a3+4a1 , 则 ,∵ ,∴ ,
解得 或 (舍),∵各项均为正数,∴ ,又∵等比数列{an}的前4项为和为15,
∴ ,解得 ,∴ ,
故答案为:C.
【分析】由已知利用等比数列的通项公式列式,得到q=2,再由前4项为和为15列式,解得 ,即可求出 的值.
3.【答案】 B
【考点】等比数列的性质
【解析】【解答】因为头顶至肚脐的长度与肚脐至足底的长度之比是 ,成为黄金分割比例),此外,头顶至咽喉的长度与咽喉至肚脐的长度也是 ,所以设咽喉到肚脐的长度为 厘米,肚脐到腰的长度为 厘米,依题意得:
所以身高为 所以最接近的身高是175厘米。
故答案为:B
【分析】利用黄金比例的概念结合对应边成比例求出某人满足要求最接近的身高。
4.【答案】 A
【考点】等差数列
【解析】【解答】 利用等差数列通项公式和等差数列前n项和公式得,
①
②
①②联立求出:
故答案为:A
【分析】利用等差数列通项公式和等差数列前n项和公式结合已知条件求出等差数列的首项和公差,从而求出等差数列的通项公式。
二、填空题
5.【答案】 16
【考点】等差数列的前n项和
【解析】【解答】 数列 是等差数列,又
利用等差数列通项公式 得:
①
是等差数列 前n项和,且
利用等差数列前n项和公式 得:
②
①②联立,得:
【分析】根据已知条件结合等差数列通项公式和等差数列前n项和公式求出等差数列的首项和公差,再利用等差数列前n项和公式求出等差数列前8项的和。
6.【答案】 100
【考点】等差数列的前n项和
【解析】【解答】解:∵ ,∴ ,∴ ,
∴ ,
故答案为:100.
【分析】由已知列式 ,得到 ,代入等差数列的求和公式即可求值.
7.【答案】 4
【考点】等差数列的前n项和
【解析】【解答】解:∵等差数列{an}中 ,∴ ,∴ ,
故答案为:4.
【分析】由已知得到 ,利用等差数列的求和公式,代入化简即可求值.
8.【答案】 0 ;-10
【考点】等差数列
【解析】【解答】解: ,
解得 ,所以 ,
,
根据二次函数的性质,当n=4或5时, 有最小值-10.
故答案为:0;-10.
【分析】根据等差数列的通项公式和前n项和公式,解方程组求出首项和公差,即可求出 和 ,结合二次函数的性质求出最小值即可.
9.【答案】
【考点】等比数列
【解析】【解答】设等比数列的公比为q,利用等比数列的前n项和公式,
当 时,
当 时,
由求根公式求出q的值,根据题意, 从而确定q的值。
【分析】利用分类讨论的方法结合等比数列前n项和公式求出q的值,从而利用 与 的关系式结合 的值求出 的值。
10.【答案】
【考点】等比数列
【解析】【解答】 利用等比数列通项公式得,
①
②
①②联立求出:
【分析】利用等比数列通项公式和等比数列前n项和公式结合已知条件 求出等比数列的公比,从而利用等比数列的首项和公比求出等比数列的前5项的和。
同课章节目录
