2019年高考数学真题分类汇编专题09:三角函数(基础题)
文档属性
| 名称 | 2019年高考数学真题分类汇编专题09:三角函数(基础题) |  | |
| 格式 | zip | ||
| 文件大小 | 351.6KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-06-14 16:08:06 | ||
图片预览




文档简介
2019年高考数学真题分类汇编专题09:三角函数(基础题)
一、单选题
1.(2019?天津)已知函数 是奇函数,且 的最小正周期为 ,将 的图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),所得图象对应的函数为 .若 ,则 ( ??)
A.?-2????????????????????????????????????????B.?- ????????????????????????????????????????C.?????????????????????????????????????????D.?2
2.(2019?天津)已知函数 是奇函数,将 的图像上所有点的横坐标伸长到原来的2倍(纵坐标不变),所得图像对应的函数为 .若 的最小正周期为 ,且 ,则 ( ??)
A.????????????????????????????????????????B.????????????????????????????????????????C.????????????????????????????????????????D.?
3.(2019?全国Ⅲ)设函数f(x)=sin(ωx+ )(ω>0),已如f(x)在[0,2π]有且仅有5个零点,下述四个结论:①f(x)在(0,2π)有且仅有3个极大值点②f(x)在(0,2π)有且仅有2个极小值点③f(x)在(0, )单调递增④ω的取值范围[ , )其中所有正确结论的编号是( ??)
A.?①④??????????????????????????????????B.?②③??????????????????????????????????C.?①②③??????????????????????????????????D.?①③④
4.(2019?卷Ⅱ)若 , 是函数f(x)= sinωx(ω>0) 两个相邻的极值点,则ω( ??)
A.?2??????????????????????????????????????????B.???????????????????????????????????????????C.?1??????????????????????????????????????????D.?
5.(2019?卷Ⅱ)已知α∈(0, ),2sin 2α=cos 2α+1,则sin α=( ??)
A.?????????????????????????????????????B.?????????????????????????????????????C.?????????????????????????????????????D.?
6.(2019?卷Ⅱ)下列函数中,以 为周期且在区间( , )单调递增的是( ??)
A.?f(x)=│cos2x│??????????????????B.?f(x)=│sin 2x│??????????????????C.?f(x)=cos│x│??????????????????D.?f(x)= sin│x│
7.(2019?北京)如图,A,B是半径为2的圆周上的定点,P为圆周上的动点,∠APB是锐角,大小为β.图中阴影区域的面积的最大值为( ??)
A.?4β+4cosβ?????????????????????????B.?4β+4sinβ?????????????????????????C.?2β+2cosβ?????????????????????????D.?2β+2sinβ
8.(2019?卷Ⅰ)tan255°=(?? )
A.??????????????????????????????B.??????????????????????????????C.??????????????????????????????D.?
9.(2019?卷Ⅰ)?ABC的内角A,B,C的对边分别为a,b,c,已知asinA-bsinB=4csinC,cosA= ,则 =(?? )
A.?6???????????????????????????????????????????B.?5???????????????????????????????????????????C.?4???????????????????????????????????????????D.?3
二、填空题
10.(2019?江苏)已知 ,则 的值是________.
11.(2019?浙江)在△ABC中,∠ABC=90°,AB=4,BC=3,点D在线段AC上,若∠BDC=45°,则BD=________.COS∠ABD=________
12.(2019?卷Ⅱ)△ABC的内角 , , 的对边分别为 , , ,知 ,则 =________
13.(2019?卷Ⅱ) 的内角 的对边分别为 .若 ,则 的面积为________.
14.(2019?北京)函数f(x)=sin22x的最小正周期是________.
15.(2019?卷Ⅰ)函数f(x)=sin(2x+ )-3cosx的最小值为________.
答案解析部分
一、单选题
1.【答案】 C
【考点】函数y=Asin(ωx+φ)的图象变换
【解析】【解答】由函数 是奇函数,得 ,即 得
由 的最小正周期为 ,得 ,
将 的图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),得
由 得 即
故
故答案为:C
【分析】由奇函数得 ,即 得 ,由周期求出ω,再根据函数 的图象变换规律,得出 ,再代入 求出A的值,进而得出 的值。
2.【答案】 A
【考点】函数y=Asin(ωx+φ)的图象变换
【解析】【解答】由函数 是奇函数,得 ,即 得
由 的图像上所有点的横坐标伸长到原来的2倍(纵坐标不变),所得图像对应的函数为 .若 的最小正周期为 ,
得 的最小正周期为 ,
故
由 得 即
故
故答案为:C
【分析】由奇函数得 ,即 得 ,由 的图像上所有点的横坐标伸长到原来的2倍(纵坐标不变),所得图像对应的函数为 的最小正周期为 ,
得 的最小正周期为 ,求出ω,进而得出 , ,再代入 求出A的值,进而得出 。
3.【答案】 D
【考点】由y=Asin(ωx+φ)的部分图象确定其解析式
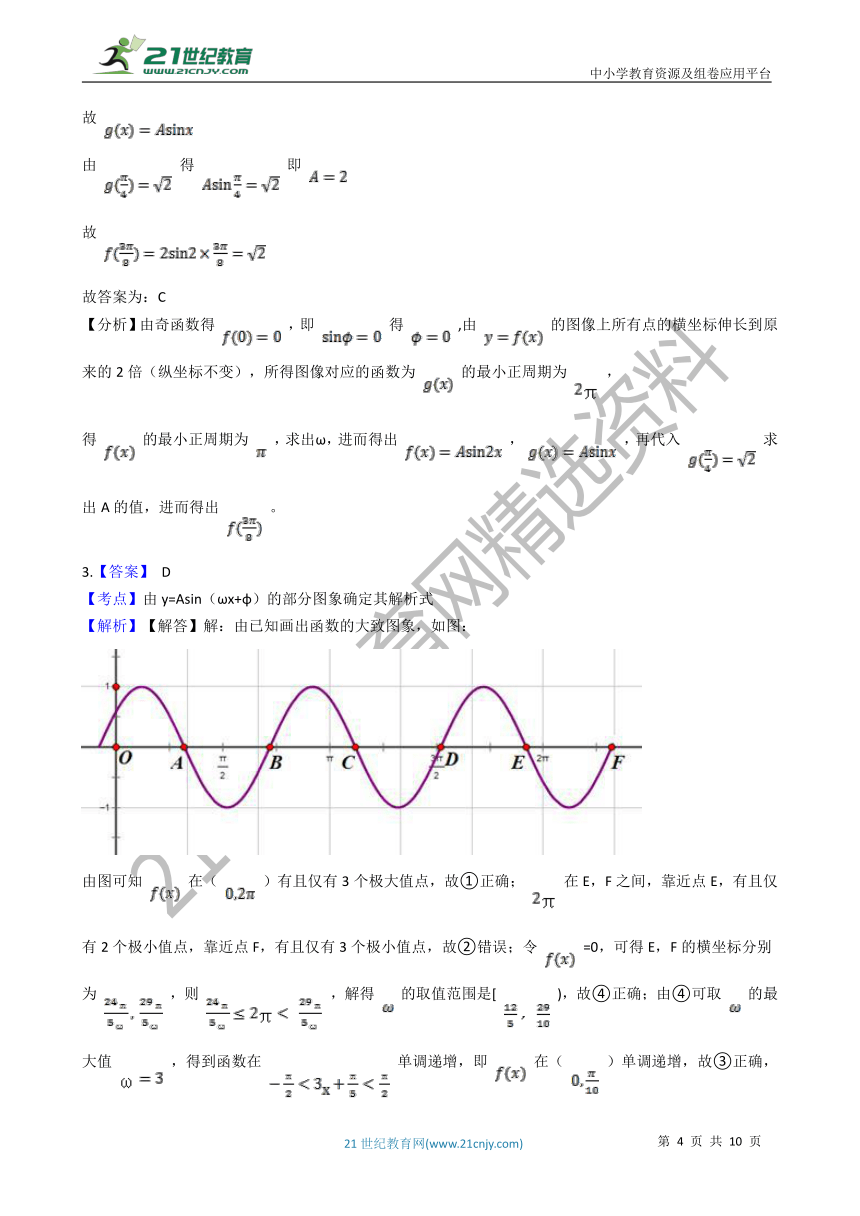
【解析】【解答】解:由已知画出函数的大致图象,如图:
由图可知 在( )有且仅有3个极大值点,故①正确; 在E,F之间,靠近点E,有且仅有2个极小值点,靠近点F,有且仅有3个极小值点,故②错误;令 =0,可得E,F的横坐标分别为 ,则 ,解得 的取值范围是[ ),故④正确;由④可取 的最大值 ,得到函数在 单调递增,即 在( )单调递增,故③正确,
故答案为:D.
【分析】由已知画出函数的大致图象,利用图象得到①正确,②错误,再利用函数 的性质得到③④正确,即可得结论.
4.【答案】 A
【考点】三角函数的周期性及其求法
【解析】【解答】∵x1= ,x2= ,是函数f(x)= ( >0)两个相邻的极值点,∴函数的半个周期为 , ∴ .
故答案为:A
【分析】根据题意首先求出函数的周期再由正弦函数的周期公式代入数值求出即可。
5.【答案】 B
【考点】三角函数中的恒等变换应用
【解析】【解答】由二倍角的正弦和余弦公式整理化简原式 ,进而求出 ,代入到 , ∵a∈(0, ) , ∴ .
故答案为:B
【分析】利用二倍角的正弦和余弦公式整理化简原式即可求出 ,再由同角三角函数的关系式求出 ,结合角的取值范围可判断出 的符号为正,从而求出结果。
6.【答案】 A
【考点】三角函数的周期性及其求法,复合三角函数的单调性
【解析】【解答】因为f(x)=sinx,f(x)=cosx的周期为2π,则f(x)=|cosx|, 的周期为π,故C项,D项错误。
y=│sin2x│图象如图1,可知y=│sin2x│在( , )上单调递减,故B项错误。 图1
y=│cos2x│图象如图2,可知y=│cos2x│在( , )上单调递增,故A项正确。 图2
故答案为:A
【分析】根据题中的四个函数结合正弦函数与余弦函数的图像逐一分析即可得出结论。
7.【答案】 B
【考点】任意角的三角函数的定义
【解析】【解答】设圆心为O,根据 可知AB所对圆心角
故扇形 的面积为 ,由题意,要使阴影部分面积最大,则P到AB的距离最大,此时PO与AB垂直,
故阴影部分面积最大值
而 ,
,
故阴影部分面积最大值
故答案为:B.
【分析】根据圆周角得到圆心角,由题意,要使阴影部分面积最大,则P到AB的距离最大,此时PO与AB垂直,结合三角函数的定义,表示相应三角形的面积,即可求出阴影部分面积的最大值.
8.【答案】 D
【考点】运用诱导公式化简求值
【解析】【解答】 . 故答案为:D
【分析】利用诱导公式结合两角和的正切公式求出 的值。
9.【答案】 A
【考点】三角形中的几何计算
【解析】【解答】由已知条件 结合正弦定理,
①
利用余弦定理,得 ②
①②联立得:
故答案为:A
【分析】利用已知条件结合正弦定理和余弦定理,变形得出b,c的关系式,从而求出 的值。
二、填空题
10.【答案】
【考点】三角函数的化简求值
【解析】【解答】
【分析】利用两角和的正切公式结合已知条件求出角 的正切值,再利用角 的正弦值和余弦值与角 的正切值的关系式结合角 的正切值的取值范围求出角 的正弦值和余弦值与角 的正切值,再用角 的正切值结合两角和的正弦公式求出 的值。
11.【答案】 ;
【考点】余弦定理的应用
【解析】【解答】解:在△BCD中, 根据正弦定理
即 解得BD= ;
COS∠ABD=sin .
【分析】在△BCD中,根据正弦定理即可求出BD;根据两角差的正弦公式,即可求出相应的三角函数值.
12.【答案】
【考点】三角形中的几何计算
【解析】【解答】由正弦定理可得 , ,代入原式可得 , ∵ 的内角为A , B , C,∴sinA ∴tanB=-1, ∴ .
【分析】利用正弦定理整理化简原式即可求出tanB=-1,进而求出角B的大小。
13.【答案】
【考点】三角形中的几何计算
【解析】【解答】由余弦定理得, ,由题得:b=6,a=2c, ,代入化简得 ,
解得? c1=2 , c2=-2? (舍),则a=2c=4 ,所以
故答案为:
【分析】首先利用余弦定理代入数值求出c的值,从而求出a的值,再由三角形的面积公式代入数值求出结果即可。
14.【答案】
【考点】三角函数的周期性及其求法
【解析】【解答】解: ,
所以最小正周期 .
故答案为: .
【分析】根据余弦的二倍角公式,结合正弦函数的周期性即可求出相应的最小正周期.
15.【答案】 -4
【考点】三角函数中的恒等变换应用
【解析】【解答】
利用诱导公式和二倍角的余弦公式得: 利用换元法,令
当 时,
【分析】利用诱导公式和二倍角的余弦公式化简将函数转化为二次函数,再利用二次函数求最值的方法求出函数的最小值。
一、单选题
1.(2019?天津)已知函数 是奇函数,且 的最小正周期为 ,将 的图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),所得图象对应的函数为 .若 ,则 ( ??)
A.?-2????????????????????????????????????????B.?- ????????????????????????????????????????C.?????????????????????????????????????????D.?2
2.(2019?天津)已知函数 是奇函数,将 的图像上所有点的横坐标伸长到原来的2倍(纵坐标不变),所得图像对应的函数为 .若 的最小正周期为 ,且 ,则 ( ??)
A.????????????????????????????????????????B.????????????????????????????????????????C.????????????????????????????????????????D.?
3.(2019?全国Ⅲ)设函数f(x)=sin(ωx+ )(ω>0),已如f(x)在[0,2π]有且仅有5个零点,下述四个结论:①f(x)在(0,2π)有且仅有3个极大值点②f(x)在(0,2π)有且仅有2个极小值点③f(x)在(0, )单调递增④ω的取值范围[ , )其中所有正确结论的编号是( ??)
A.?①④??????????????????????????????????B.?②③??????????????????????????????????C.?①②③??????????????????????????????????D.?①③④
4.(2019?卷Ⅱ)若 , 是函数f(x)= sinωx(ω>0) 两个相邻的极值点,则ω( ??)
A.?2??????????????????????????????????????????B.???????????????????????????????????????????C.?1??????????????????????????????????????????D.?
5.(2019?卷Ⅱ)已知α∈(0, ),2sin 2α=cos 2α+1,则sin α=( ??)
A.?????????????????????????????????????B.?????????????????????????????????????C.?????????????????????????????????????D.?
6.(2019?卷Ⅱ)下列函数中,以 为周期且在区间( , )单调递增的是( ??)
A.?f(x)=│cos2x│??????????????????B.?f(x)=│sin 2x│??????????????????C.?f(x)=cos│x│??????????????????D.?f(x)= sin│x│
7.(2019?北京)如图,A,B是半径为2的圆周上的定点,P为圆周上的动点,∠APB是锐角,大小为β.图中阴影区域的面积的最大值为( ??)
A.?4β+4cosβ?????????????????????????B.?4β+4sinβ?????????????????????????C.?2β+2cosβ?????????????????????????D.?2β+2sinβ
8.(2019?卷Ⅰ)tan255°=(?? )
A.??????????????????????????????B.??????????????????????????????C.??????????????????????????????D.?
9.(2019?卷Ⅰ)?ABC的内角A,B,C的对边分别为a,b,c,已知asinA-bsinB=4csinC,cosA= ,则 =(?? )
A.?6???????????????????????????????????????????B.?5???????????????????????????????????????????C.?4???????????????????????????????????????????D.?3
二、填空题
10.(2019?江苏)已知 ,则 的值是________.
11.(2019?浙江)在△ABC中,∠ABC=90°,AB=4,BC=3,点D在线段AC上,若∠BDC=45°,则BD=________.COS∠ABD=________
12.(2019?卷Ⅱ)△ABC的内角 , , 的对边分别为 , , ,知 ,则 =________
13.(2019?卷Ⅱ) 的内角 的对边分别为 .若 ,则 的面积为________.
14.(2019?北京)函数f(x)=sin22x的最小正周期是________.
15.(2019?卷Ⅰ)函数f(x)=sin(2x+ )-3cosx的最小值为________.
答案解析部分
一、单选题
1.【答案】 C
【考点】函数y=Asin(ωx+φ)的图象变换
【解析】【解答】由函数 是奇函数,得 ,即 得
由 的最小正周期为 ,得 ,
将 的图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),得
由 得 即
故
故答案为:C
【分析】由奇函数得 ,即 得 ,由周期求出ω,再根据函数 的图象变换规律,得出 ,再代入 求出A的值,进而得出 的值。
2.【答案】 A
【考点】函数y=Asin(ωx+φ)的图象变换
【解析】【解答】由函数 是奇函数,得 ,即 得
由 的图像上所有点的横坐标伸长到原来的2倍(纵坐标不变),所得图像对应的函数为 .若 的最小正周期为 ,
得 的最小正周期为 ,
故
由 得 即
故
故答案为:C
【分析】由奇函数得 ,即 得 ,由 的图像上所有点的横坐标伸长到原来的2倍(纵坐标不变),所得图像对应的函数为 的最小正周期为 ,
得 的最小正周期为 ,求出ω,进而得出 , ,再代入 求出A的值,进而得出 。
3.【答案】 D
【考点】由y=Asin(ωx+φ)的部分图象确定其解析式
【解析】【解答】解:由已知画出函数的大致图象,如图:
由图可知 在( )有且仅有3个极大值点,故①正确; 在E,F之间,靠近点E,有且仅有2个极小值点,靠近点F,有且仅有3个极小值点,故②错误;令 =0,可得E,F的横坐标分别为 ,则 ,解得 的取值范围是[ ),故④正确;由④可取 的最大值 ,得到函数在 单调递增,即 在( )单调递增,故③正确,
故答案为:D.
【分析】由已知画出函数的大致图象,利用图象得到①正确,②错误,再利用函数 的性质得到③④正确,即可得结论.
4.【答案】 A
【考点】三角函数的周期性及其求法
【解析】【解答】∵x1= ,x2= ,是函数f(x)= ( >0)两个相邻的极值点,∴函数的半个周期为 , ∴ .
故答案为:A
【分析】根据题意首先求出函数的周期再由正弦函数的周期公式代入数值求出即可。
5.【答案】 B
【考点】三角函数中的恒等变换应用
【解析】【解答】由二倍角的正弦和余弦公式整理化简原式 ,进而求出 ,代入到 , ∵a∈(0, ) , ∴ .
故答案为:B
【分析】利用二倍角的正弦和余弦公式整理化简原式即可求出 ,再由同角三角函数的关系式求出 ,结合角的取值范围可判断出 的符号为正,从而求出结果。
6.【答案】 A
【考点】三角函数的周期性及其求法,复合三角函数的单调性
【解析】【解答】因为f(x)=sinx,f(x)=cosx的周期为2π,则f(x)=|cosx|, 的周期为π,故C项,D项错误。
y=│sin2x│图象如图1,可知y=│sin2x│在( , )上单调递减,故B项错误。 图1
y=│cos2x│图象如图2,可知y=│cos2x│在( , )上单调递增,故A项正确。 图2
故答案为:A
【分析】根据题中的四个函数结合正弦函数与余弦函数的图像逐一分析即可得出结论。
7.【答案】 B
【考点】任意角的三角函数的定义
【解析】【解答】设圆心为O,根据 可知AB所对圆心角
故扇形 的面积为 ,由题意,要使阴影部分面积最大,则P到AB的距离最大,此时PO与AB垂直,
故阴影部分面积最大值
而 ,
,
故阴影部分面积最大值
故答案为:B.
【分析】根据圆周角得到圆心角,由题意,要使阴影部分面积最大,则P到AB的距离最大,此时PO与AB垂直,结合三角函数的定义,表示相应三角形的面积,即可求出阴影部分面积的最大值.
8.【答案】 D
【考点】运用诱导公式化简求值
【解析】【解答】 . 故答案为:D
【分析】利用诱导公式结合两角和的正切公式求出 的值。
9.【答案】 A
【考点】三角形中的几何计算
【解析】【解答】由已知条件 结合正弦定理,
①
利用余弦定理,得 ②
①②联立得:
故答案为:A
【分析】利用已知条件结合正弦定理和余弦定理,变形得出b,c的关系式,从而求出 的值。
二、填空题
10.【答案】
【考点】三角函数的化简求值
【解析】【解答】
【分析】利用两角和的正切公式结合已知条件求出角 的正切值,再利用角 的正弦值和余弦值与角 的正切值的关系式结合角 的正切值的取值范围求出角 的正弦值和余弦值与角 的正切值,再用角 的正切值结合两角和的正弦公式求出 的值。
11.【答案】 ;
【考点】余弦定理的应用
【解析】【解答】解:在△BCD中, 根据正弦定理
即 解得BD= ;
COS∠ABD=sin .
【分析】在△BCD中,根据正弦定理即可求出BD;根据两角差的正弦公式,即可求出相应的三角函数值.
12.【答案】
【考点】三角形中的几何计算
【解析】【解答】由正弦定理可得 , ,代入原式可得 , ∵ 的内角为A , B , C,∴sinA ∴tanB=-1, ∴ .
【分析】利用正弦定理整理化简原式即可求出tanB=-1,进而求出角B的大小。
13.【答案】
【考点】三角形中的几何计算
【解析】【解答】由余弦定理得, ,由题得:b=6,a=2c, ,代入化简得 ,
解得? c1=2 , c2=-2? (舍),则a=2c=4 ,所以
故答案为:
【分析】首先利用余弦定理代入数值求出c的值,从而求出a的值,再由三角形的面积公式代入数值求出结果即可。
14.【答案】
【考点】三角函数的周期性及其求法
【解析】【解答】解: ,
所以最小正周期 .
故答案为: .
【分析】根据余弦的二倍角公式,结合正弦函数的周期性即可求出相应的最小正周期.
15.【答案】 -4
【考点】三角函数中的恒等变换应用
【解析】【解答】
利用诱导公式和二倍角的余弦公式得: 利用换元法,令
当 时,
【分析】利用诱导公式和二倍角的余弦公式化简将函数转化为二次函数,再利用二次函数求最值的方法求出函数的最小值。
同课章节目录
