2019年高考数学真题分类汇编专题11:空间几何体(基础题)
文档属性
| 名称 | 2019年高考数学真题分类汇编专题11:空间几何体(基础题) |  | |
| 格式 | zip | ||
| 文件大小 | 702.3KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-06-14 16:18:30 | ||
图片预览


文档简介
2019年高考数学真题分类汇编专题11:空间几何体(基础题)
一、单选题
1.(2019?浙江)设三棱锥V-ABC的底面是正三角形,侧棱长均相等,P是棱VA上的点,(不含端点),记直线PB与直线AC所成角为α.直线PB与平面ABC所成角为β.二面角P-AC-B的平面角为γ。则( ??)
A.?β<γ,a <γ????????????????????B.?β<α,β<γ????????????????????C.?β<α,γ<α????????????????????D.?α<β , γ<β
2.(2019?卷Ⅱ)设α,β为两个平面,则α∥β的充要条件是( ??)
A.?α内有无数条直线与β平行???????????????????????????????????B.?α内有两条相交直线与β平行 C.?α,β平行于同一条直线????????????????????????????????????? ??D.?α,β垂直于同一平面
3.(2019?卷Ⅰ)已知三棱锥P-ABC的四个顶点在球O的球面上,PA=PB=PC,?ABC是边长为2的正三角形,E、F,分别是PA,AB的中点, CEF=90°,则球O的体积为(?? )
A.???????????????????????????????????B.???????????????????????????????????C.???????????????????????????????????D.?
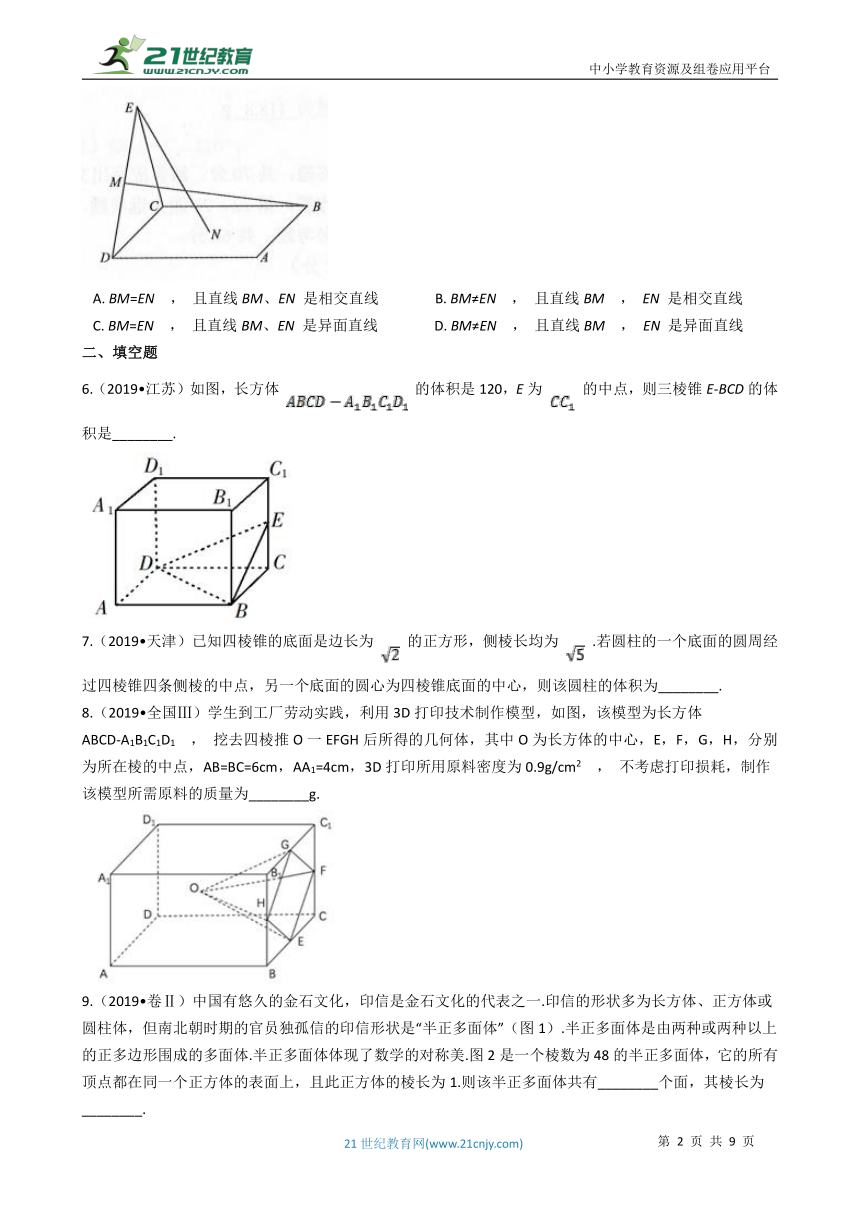
4.(2019?浙江)祖暅是我国南北朝时代的伟大科学家,他提出的“幂势既同,则积不容异”称为祖暅原理,利用该原理可以得到柱体的体积公式V柱体=sh,其中s是柱体的底面积,h是柱体的高。若某柱体的三视图如图所示,则该柱体的体积是( ??)
A.?158???????????????????????????????????????B.?162???????????????????????????????????????C.?182???????????????????????????????????????D.?32
5.(2019?全国Ⅲ)如图,点N为正方形ABCD的中心,△ECD为正三角形,平面ECD⊥平面ABCD , M是线段ED的中点,则( ??)
A.?BM=EN , 且直线BM、EN 是相交直线????????????????B.?BM≠EN , 且直线BM , EN 是相交直线 C.?BM=EN , 且直线BM、EN 是异面直线????????????????D.?BM≠EN , 且直线BM , EN 是异面直线
二、填空题
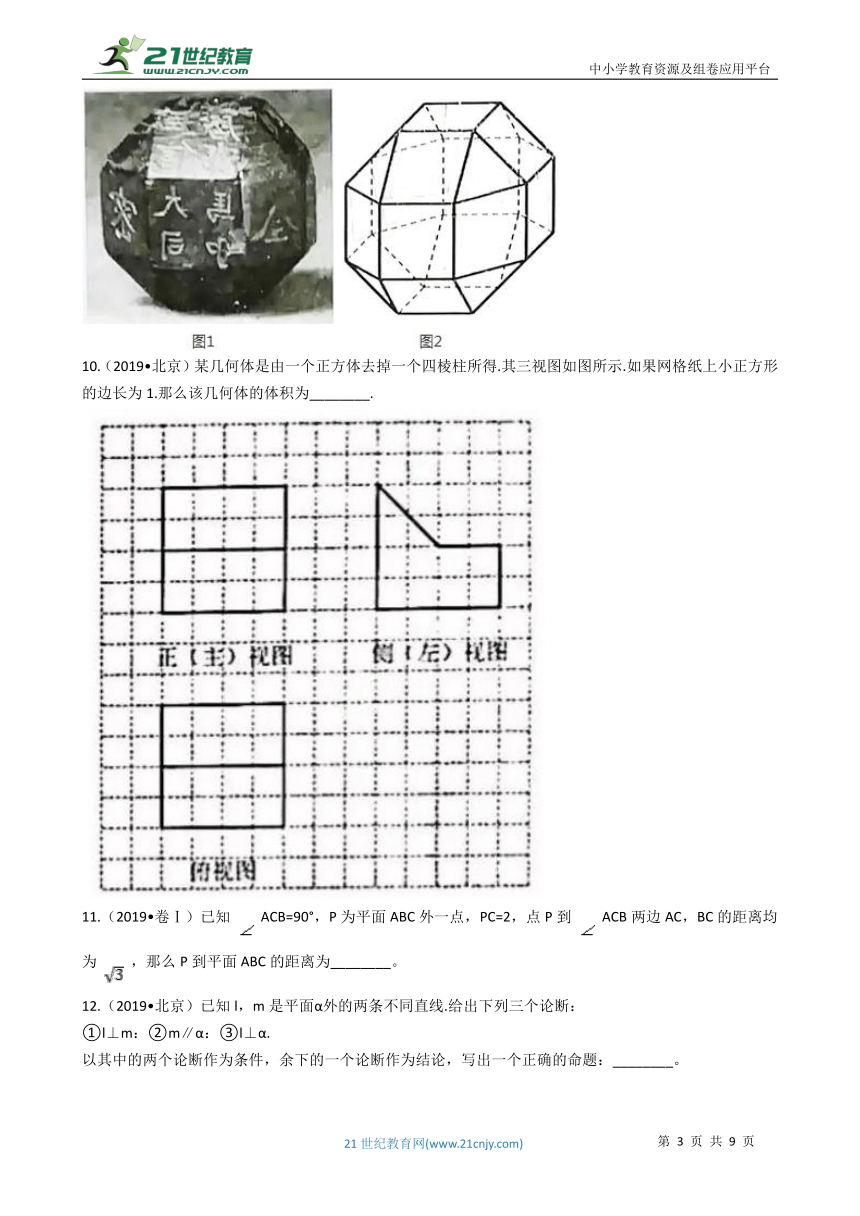
6.(2019?江苏)如图,长方体 的体积是120,E为 的中点,则三棱锥E-BCD的体积是________.
7.(2019?天津)已知四棱锥的底面是边长为 的正方形,侧棱长均为 .若圆柱的一个底面的圆周经过四棱锥四条侧棱的中点,另一个底面的圆心为四棱锥底面的中心,则该圆柱的体积为________.
8.(2019?全国Ⅲ)学生到工厂劳动实践,利用3D打印技术制作模型,如图,该模型为长方体ABCD-A1B1C1D1 , 挖去四棱推O一EFGH后所得的几何体,其中O为长方体的中心,E,F,G,H,分别为所在棱的中点,AB=BC=6cm,AA1=4cm,3D打印所用原料密度为0.9g/cm2 , 不考虑打印损耗,制作该模型所需原料的质量为________g.
9.(2019?卷Ⅱ)中国有悠久的金石文化,印信是金石文化的代表之一.印信的形状多为长方体、正方体或圆柱体,但南北朝时期的官员独孤信的印信形状是“半正多面体”(图1).半正多面体是由两种或两种以上的正多边形围成的多面体.半正多面体体现了数学的对称美.图2是一个棱数为48的半正多面体,它的所有顶点都在同一个正方体的表面上,且此正方体的棱长为1.则该半正多面体共有________个面,其棱长为________.
10.(2019?北京)某几何体是由一个正方体去掉一个四棱柱所得.其三视图如图所示.如果网格纸上小正方形的边长为1.那么该几何体的体积为________.
11.(2019?卷Ⅰ)已知 ACB=90°,P为平面ABC外一点,PC=2,点P到 ACB两边AC,BC的距离均为 ,那么P到平面ABC的距离为________。
12.(2019?北京)已知l,m是平面α外的两条不同直线.给出下列三个论断:
①l⊥m:②m∥α:③l⊥α.
以其中的两个论断作为条件,余下的一个论断作为结论,写出一个正确的命题:________。
答案解析部分
一、单选题
1.【答案】 B
【考点】异面直线及其所成的角,直线与平面所成的角,二面角的平面角及求法
【解析】【解答】如图 为 中点, 在底面 的投影为 ,则 在底面投影 在线段 上,过 作 垂直 ,
易得 ,过 作 交 于 ,过 作 ,交 于 ,则 ,则 ,即 , ,即 ,综上所述, B正确.
故答案为:B
【分析】根据异面直线所成的角、直线与平面所成的角、二面角的概念,以及各种角的计算.应用三角函数知识求解,进而比较大小即可.
2.【答案】 B
【考点】空间中直线与平面之间的位置关系
【解析】【解答】A选项中α面内的无数条直线不一定是两条相交直线C选项中平行于同一条直线的两个平面也可以相交D选项垂直于同一个平面的两个平面也可以相交。
故答案为:B
【分析】利用两个平面平行的判定定理,一个平面内的两条相交直线都平行于另一个平面则两个平面平行,逐一判断选项即可得出正确答案。
3.【答案】 D
【考点】球内接多面体
【解析】【解答】设 则
在 中,由中线定理得:
利用勾股定理,得:
求出 所以
【分析】利用三棱锥P-ABC的结构特征结合三棱锥与球O的位置关系,再利用中线定理和勾股定理求出球O的半径,再利用球的体积公式结合球的半径求出球O的体积。
4.【答案】 B
【考点】由三视图求面积、体积
【解析】【解答】根据三视图,确定几何体为五棱柱,
其底面积 ,
所以体积V=27 .
故答案为:B.
【分析】根据三视图确定几何体的结构特征,根据祖暅原理,即可求出相应的体积.
5.【答案】 B
【考点】平面的基本性质及推论
【解析】【解答】解:连接BD,BE,MN,如图:
∵M,N分别是线段ED,BD的中点,∴MN∥BE,∴直线MN,BE确定一个平面,
∴直线BM,EN 是相交直线,设正方形ABCD的的边长为a,则DE=a,DB= a,
∵DE≠DB,∴△BMD与△END不全等,∴BM≠EN,
故答案为:B.
【分析】由已知可证MN∥BE,得到直线MN,BE确定一个平面,可证直线BM,EN 是相交直线,再由△BMD与△END不全等,得到BM≠EN,即可判断得结论.
二、填空题
6.【答案】 10
【考点】棱柱、棱锥、棱台的体积
【解析】【解答】
在长方体中, 平面 又 在 上, 平面
是三棱锥E-BCD的高,
长方体的体积为:
长方体 的体积是120,
又 为 的中点,
又
【分析】根据长方体的结构特征结合线面垂直和中点的性质,用三棱锥体积公式结合三棱锥体积与长方体体积的关系式,用长方体的体积求出三棱锥的体积。
7.【答案】
【考点】旋转体(圆柱、圆锥、圆台)
【解析】【解答】∵四棱锥的底面是边长为 的正方形,侧棱长均为
连接 ,
设四棱锥的高为 , 是底面的中心。
∴ ,
在 中,
∵圆柱的一个底面的圆周经过四棱锥四条侧棱的中点,另一个底面的圆心为四棱锥底面的中心,
∴圆柱底面的半径 ,圆柱的高
∴圆柱的体积 ??????
【分析】本题主要考查圆柱的体积,通过求出四棱锥的高,底面的对角线,进而得出圆柱底面的半径及圆柱的高,最后求出圆柱的体积。?????????????????????????????????????????
8.【答案】 118.8
【考点】组合几何体的面积、体积问题
【解析】【解答】解:∵E,F,G,H分别为所在棱的中点, ,
∴四棱锥O-—EFGH的体积 ,
又∵长方体 的体积 ,∴该模型的体积 ,
∴制作该模型所需原料的质量为132×0.9=118.8g,
故答案为118.8.
【分析】由已知得到四棱锥O-—EFGH和长方体 的体积,求出该模型的体积 ,即可求出制作该模型所需原料的质量.
9.【答案】 26;
【考点】构成空间几何体的基本元素
【解析】【解答】结合图形的对称性数一数即可得到面的个数为26个。
根据题意补全该半正多面体的正方体,其俯视图为,
设该半正多面体的棱长为a,则有正方体的棱
长为 , ∴ .
【分析】利用空间想象力结合图形的对称性数出面的个数,再补全正方体借助俯视图得出几何关系进而求出该正多面体的棱长。
10.【答案】 40
【考点】由三视图求面积、体积
【解析】【解答】根据三视图,可知正方体体积 ,
去掉的四棱柱体积 ,
故该几何体的体积V=64-24=40.
故答案为40.
【分析】根据三视图确定几何体的结构特征,求出相应的体积即可.
11.【答案】
【考点】点、线、面间的距离计算
【解析】【解答】设点P在平面ABC的距离为d,设点P在平面ABC投影点为O,所以d=PO,过点P作BC边的垂线,垂足为D,连接OP,OC,OD,则 即为PC与平面ABC所成的平面角,因为点P到 ACB两边AC,BC的距离均为 ,故点O在 ACB的角平分线上,即 由于PC=2, 则三角形PCD在地底面上的投影三角形OCD为等腰直角三角形,
利用勾股定理得:
点P在平面ABC投影点为O,
所以三角形POC是直角三角形,利用勾股定理得:
【分析】利用投影原理结合线面垂直的定义证出线线垂直,再利用线线垂直满足勾股定理,用勾股定理求出点P在平面ABC的距离。
12.【答案】 若②③,则①
【考点】复合命题的真假,空间中直线与平面之间的位置关系
【解析】【解答】若 ,则 垂直于 内任意一条直线,
若 ,则 ;
故答案为若②③,则①.
【分析】根据空间直线与平面垂直的性质,即可得到相应的结论.
一、单选题
1.(2019?浙江)设三棱锥V-ABC的底面是正三角形,侧棱长均相等,P是棱VA上的点,(不含端点),记直线PB与直线AC所成角为α.直线PB与平面ABC所成角为β.二面角P-AC-B的平面角为γ。则( ??)
A.?β<γ,a <γ????????????????????B.?β<α,β<γ????????????????????C.?β<α,γ<α????????????????????D.?α<β , γ<β
2.(2019?卷Ⅱ)设α,β为两个平面,则α∥β的充要条件是( ??)
A.?α内有无数条直线与β平行???????????????????????????????????B.?α内有两条相交直线与β平行 C.?α,β平行于同一条直线????????????????????????????????????? ??D.?α,β垂直于同一平面
3.(2019?卷Ⅰ)已知三棱锥P-ABC的四个顶点在球O的球面上,PA=PB=PC,?ABC是边长为2的正三角形,E、F,分别是PA,AB的中点, CEF=90°,则球O的体积为(?? )
A.???????????????????????????????????B.???????????????????????????????????C.???????????????????????????????????D.?
4.(2019?浙江)祖暅是我国南北朝时代的伟大科学家,他提出的“幂势既同,则积不容异”称为祖暅原理,利用该原理可以得到柱体的体积公式V柱体=sh,其中s是柱体的底面积,h是柱体的高。若某柱体的三视图如图所示,则该柱体的体积是( ??)
A.?158???????????????????????????????????????B.?162???????????????????????????????????????C.?182???????????????????????????????????????D.?32
5.(2019?全国Ⅲ)如图,点N为正方形ABCD的中心,△ECD为正三角形,平面ECD⊥平面ABCD , M是线段ED的中点,则( ??)
A.?BM=EN , 且直线BM、EN 是相交直线????????????????B.?BM≠EN , 且直线BM , EN 是相交直线 C.?BM=EN , 且直线BM、EN 是异面直线????????????????D.?BM≠EN , 且直线BM , EN 是异面直线
二、填空题
6.(2019?江苏)如图,长方体 的体积是120,E为 的中点,则三棱锥E-BCD的体积是________.
7.(2019?天津)已知四棱锥的底面是边长为 的正方形,侧棱长均为 .若圆柱的一个底面的圆周经过四棱锥四条侧棱的中点,另一个底面的圆心为四棱锥底面的中心,则该圆柱的体积为________.
8.(2019?全国Ⅲ)学生到工厂劳动实践,利用3D打印技术制作模型,如图,该模型为长方体ABCD-A1B1C1D1 , 挖去四棱推O一EFGH后所得的几何体,其中O为长方体的中心,E,F,G,H,分别为所在棱的中点,AB=BC=6cm,AA1=4cm,3D打印所用原料密度为0.9g/cm2 , 不考虑打印损耗,制作该模型所需原料的质量为________g.
9.(2019?卷Ⅱ)中国有悠久的金石文化,印信是金石文化的代表之一.印信的形状多为长方体、正方体或圆柱体,但南北朝时期的官员独孤信的印信形状是“半正多面体”(图1).半正多面体是由两种或两种以上的正多边形围成的多面体.半正多面体体现了数学的对称美.图2是一个棱数为48的半正多面体,它的所有顶点都在同一个正方体的表面上,且此正方体的棱长为1.则该半正多面体共有________个面,其棱长为________.
10.(2019?北京)某几何体是由一个正方体去掉一个四棱柱所得.其三视图如图所示.如果网格纸上小正方形的边长为1.那么该几何体的体积为________.
11.(2019?卷Ⅰ)已知 ACB=90°,P为平面ABC外一点,PC=2,点P到 ACB两边AC,BC的距离均为 ,那么P到平面ABC的距离为________。
12.(2019?北京)已知l,m是平面α外的两条不同直线.给出下列三个论断:
①l⊥m:②m∥α:③l⊥α.
以其中的两个论断作为条件,余下的一个论断作为结论,写出一个正确的命题:________。
答案解析部分
一、单选题
1.【答案】 B
【考点】异面直线及其所成的角,直线与平面所成的角,二面角的平面角及求法
【解析】【解答】如图 为 中点, 在底面 的投影为 ,则 在底面投影 在线段 上,过 作 垂直 ,
易得 ,过 作 交 于 ,过 作 ,交 于 ,则 ,则 ,即 , ,即 ,综上所述, B正确.
故答案为:B
【分析】根据异面直线所成的角、直线与平面所成的角、二面角的概念,以及各种角的计算.应用三角函数知识求解,进而比较大小即可.
2.【答案】 B
【考点】空间中直线与平面之间的位置关系
【解析】【解答】A选项中α面内的无数条直线不一定是两条相交直线C选项中平行于同一条直线的两个平面也可以相交D选项垂直于同一个平面的两个平面也可以相交。
故答案为:B
【分析】利用两个平面平行的判定定理,一个平面内的两条相交直线都平行于另一个平面则两个平面平行,逐一判断选项即可得出正确答案。
3.【答案】 D
【考点】球内接多面体
【解析】【解答】设 则
在 中,由中线定理得:
利用勾股定理,得:
求出 所以
【分析】利用三棱锥P-ABC的结构特征结合三棱锥与球O的位置关系,再利用中线定理和勾股定理求出球O的半径,再利用球的体积公式结合球的半径求出球O的体积。
4.【答案】 B
【考点】由三视图求面积、体积
【解析】【解答】根据三视图,确定几何体为五棱柱,
其底面积 ,
所以体积V=27 .
故答案为:B.
【分析】根据三视图确定几何体的结构特征,根据祖暅原理,即可求出相应的体积.
5.【答案】 B
【考点】平面的基本性质及推论
【解析】【解答】解:连接BD,BE,MN,如图:
∵M,N分别是线段ED,BD的中点,∴MN∥BE,∴直线MN,BE确定一个平面,
∴直线BM,EN 是相交直线,设正方形ABCD的的边长为a,则DE=a,DB= a,
∵DE≠DB,∴△BMD与△END不全等,∴BM≠EN,
故答案为:B.
【分析】由已知可证MN∥BE,得到直线MN,BE确定一个平面,可证直线BM,EN 是相交直线,再由△BMD与△END不全等,得到BM≠EN,即可判断得结论.
二、填空题
6.【答案】 10
【考点】棱柱、棱锥、棱台的体积
【解析】【解答】
在长方体中, 平面 又 在 上, 平面
是三棱锥E-BCD的高,
长方体的体积为:
长方体 的体积是120,
又 为 的中点,
又
【分析】根据长方体的结构特征结合线面垂直和中点的性质,用三棱锥体积公式结合三棱锥体积与长方体体积的关系式,用长方体的体积求出三棱锥的体积。
7.【答案】
【考点】旋转体(圆柱、圆锥、圆台)
【解析】【解答】∵四棱锥的底面是边长为 的正方形,侧棱长均为
连接 ,
设四棱锥的高为 , 是底面的中心。
∴ ,
在 中,
∵圆柱的一个底面的圆周经过四棱锥四条侧棱的中点,另一个底面的圆心为四棱锥底面的中心,
∴圆柱底面的半径 ,圆柱的高
∴圆柱的体积 ??????
【分析】本题主要考查圆柱的体积,通过求出四棱锥的高,底面的对角线,进而得出圆柱底面的半径及圆柱的高,最后求出圆柱的体积。?????????????????????????????????????????
8.【答案】 118.8
【考点】组合几何体的面积、体积问题
【解析】【解答】解:∵E,F,G,H分别为所在棱的中点, ,
∴四棱锥O-—EFGH的体积 ,
又∵长方体 的体积 ,∴该模型的体积 ,
∴制作该模型所需原料的质量为132×0.9=118.8g,
故答案为118.8.
【分析】由已知得到四棱锥O-—EFGH和长方体 的体积,求出该模型的体积 ,即可求出制作该模型所需原料的质量.
9.【答案】 26;
【考点】构成空间几何体的基本元素
【解析】【解答】结合图形的对称性数一数即可得到面的个数为26个。
根据题意补全该半正多面体的正方体,其俯视图为,
设该半正多面体的棱长为a,则有正方体的棱
长为 , ∴ .
【分析】利用空间想象力结合图形的对称性数出面的个数,再补全正方体借助俯视图得出几何关系进而求出该正多面体的棱长。
10.【答案】 40
【考点】由三视图求面积、体积
【解析】【解答】根据三视图,可知正方体体积 ,
去掉的四棱柱体积 ,
故该几何体的体积V=64-24=40.
故答案为40.
【分析】根据三视图确定几何体的结构特征,求出相应的体积即可.
11.【答案】
【考点】点、线、面间的距离计算
【解析】【解答】设点P在平面ABC的距离为d,设点P在平面ABC投影点为O,所以d=PO,过点P作BC边的垂线,垂足为D,连接OP,OC,OD,则 即为PC与平面ABC所成的平面角,因为点P到 ACB两边AC,BC的距离均为 ,故点O在 ACB的角平分线上,即 由于PC=2, 则三角形PCD在地底面上的投影三角形OCD为等腰直角三角形,
利用勾股定理得:
点P在平面ABC投影点为O,
所以三角形POC是直角三角形,利用勾股定理得:
【分析】利用投影原理结合线面垂直的定义证出线线垂直,再利用线线垂直满足勾股定理,用勾股定理求出点P在平面ABC的距离。
12.【答案】 若②③,则①
【考点】复合命题的真假,空间中直线与平面之间的位置关系
【解析】【解答】若 ,则 垂直于 内任意一条直线,
若 ,则 ;
故答案为若②③,则①.
【分析】根据空间直线与平面垂直的性质,即可得到相应的结论.
同课章节目录
