2019年高考数学真题分类汇编专题16:空间几何
文档属性
| 名称 | 2019年高考数学真题分类汇编专题16:空间几何 |  | |
| 格式 | zip | ||
| 文件大小 | 671.9KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-06-14 16:22:49 | ||
图片预览

文档简介
2019年高考数学真题分类汇编专题16:空间几何
一、解答题
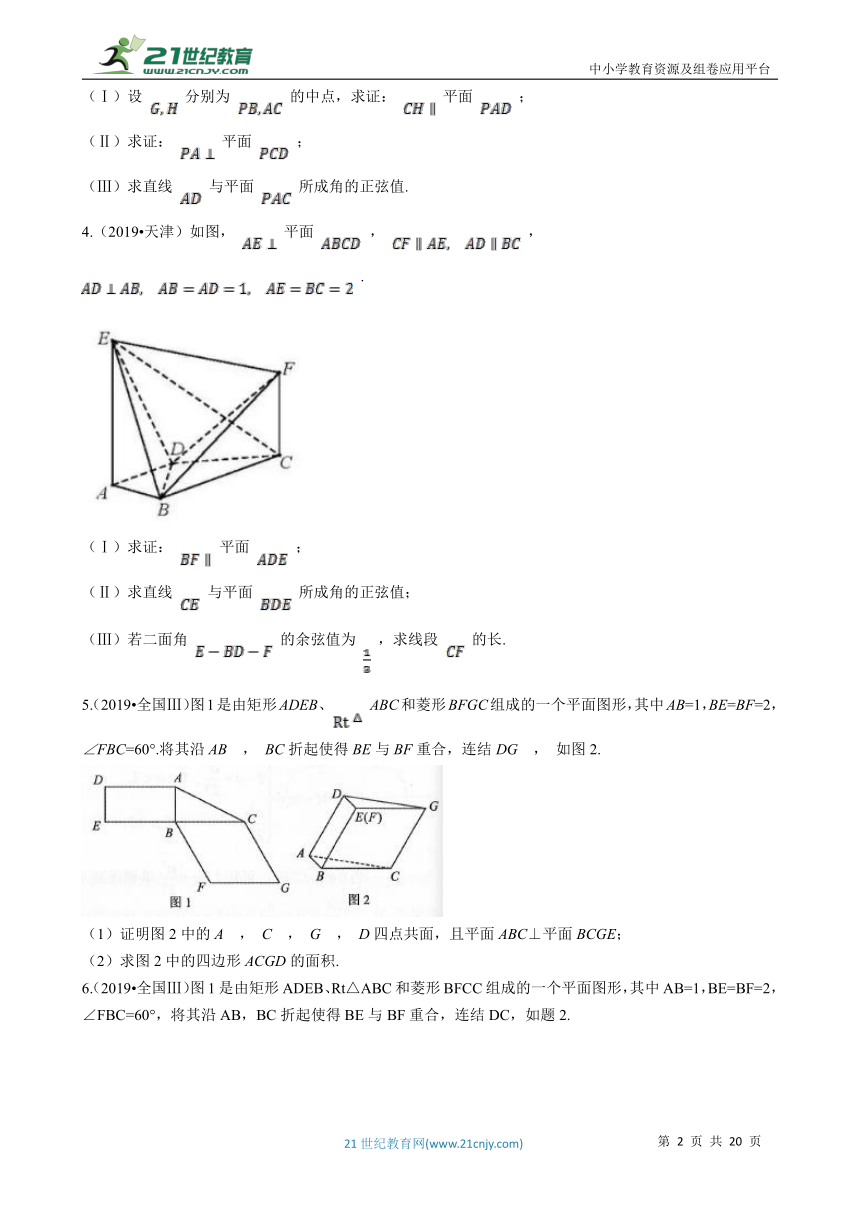
1.如图,在直三棱柱ABC-A1B1C1中,D , E分别为BC , AC的中点,AB=BC .
求证:
(1)A1B1∥平面DEC1;
(2)BE⊥C1E .
2.(2019?浙江)如图,已知三棱柱ABC-A1B1C1 , 平面A1AC1C⊥平面ABC,∠ABC=90°.∠BAC=30°,A1A=A1C=AC,E,F分别是AC,A1B1的中点
?
(1)证明:EF⊥BC
(2)求直线EF与平面A1BC所成角的余弦值.
3.(2019?天津)如图,在四棱锥 中,底面 为平行四边形, 为等边三角形,平面 平面 , , ,
(Ⅰ)设 分别为 的中点,求证: 平面 ;
(Ⅱ)求证: 平面 ;
(Ⅲ)求直线 与平面 所成角的正弦值.
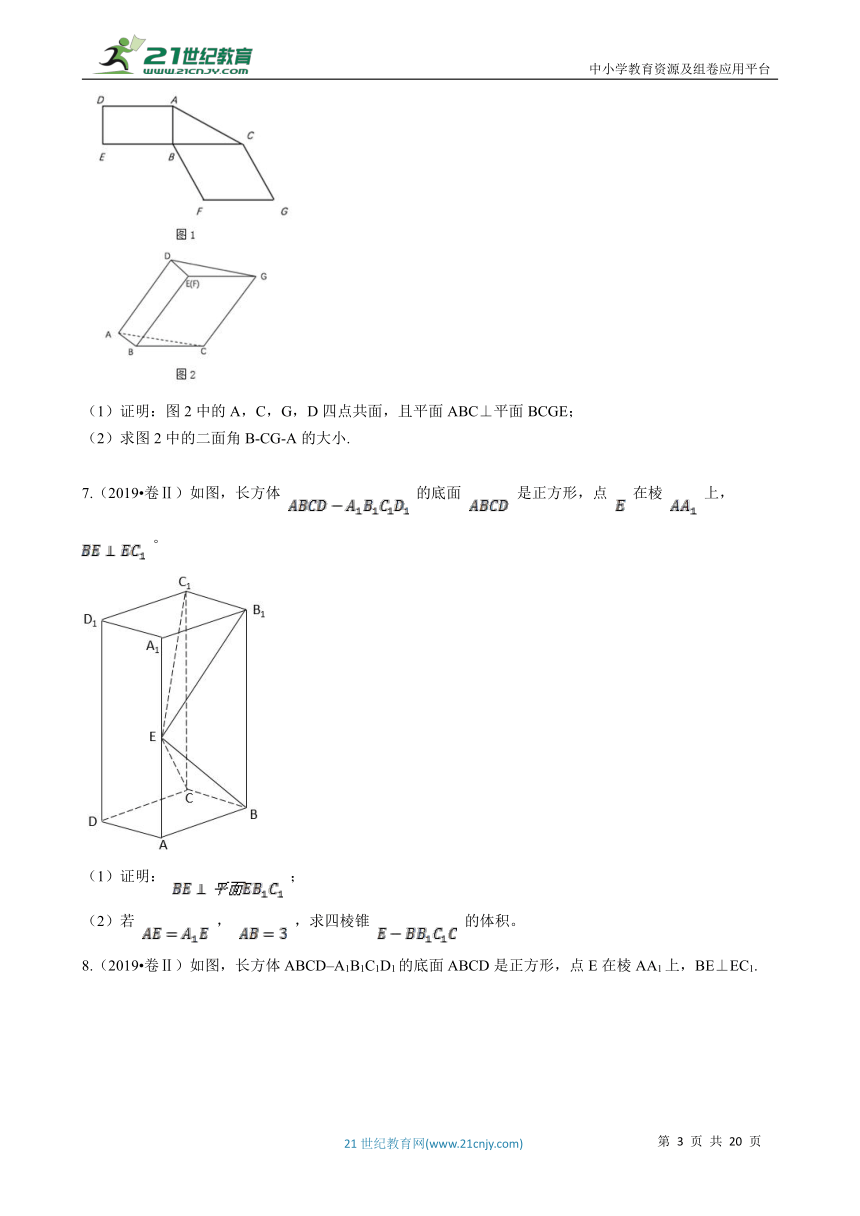
4.(2019?天津)如图, 平面 , , .
(Ⅰ)求证: 平面 ;
(Ⅱ)求直线 与平面 所成角的正弦值;
(Ⅲ)若二面角 的余弦值为 ,求线段 的长.
5.(2019?全国Ⅲ)图1是由矩形ADEB、 ABC和菱形BFGC组成的一个平面图形,其中AB=1,BE=BF=2,∠FBC=60°.将其沿AB , BC折起使得BE与BF重合,连结DG , 如图2.
(1)证明图2中的A , C , G , D四点共面,且平面ABC⊥平面BCGE;
(2)求图2中的四边形ACGD的面积.
6.(2019?全国Ⅲ)图1是由矩形ADEB、Rt△ABC和菱形BFCC组成的一个平面图形,其中AB=1,BE=BF=2,∠FBC=60°,将其沿AB,BC折起使得BE与BF重合,连结DC,如题2.
(1)证明:图2中的A,C,G,D四点共面,且平面ABC⊥平面BCGE;
(2)求图2中的二面角B-CG-A的大小.
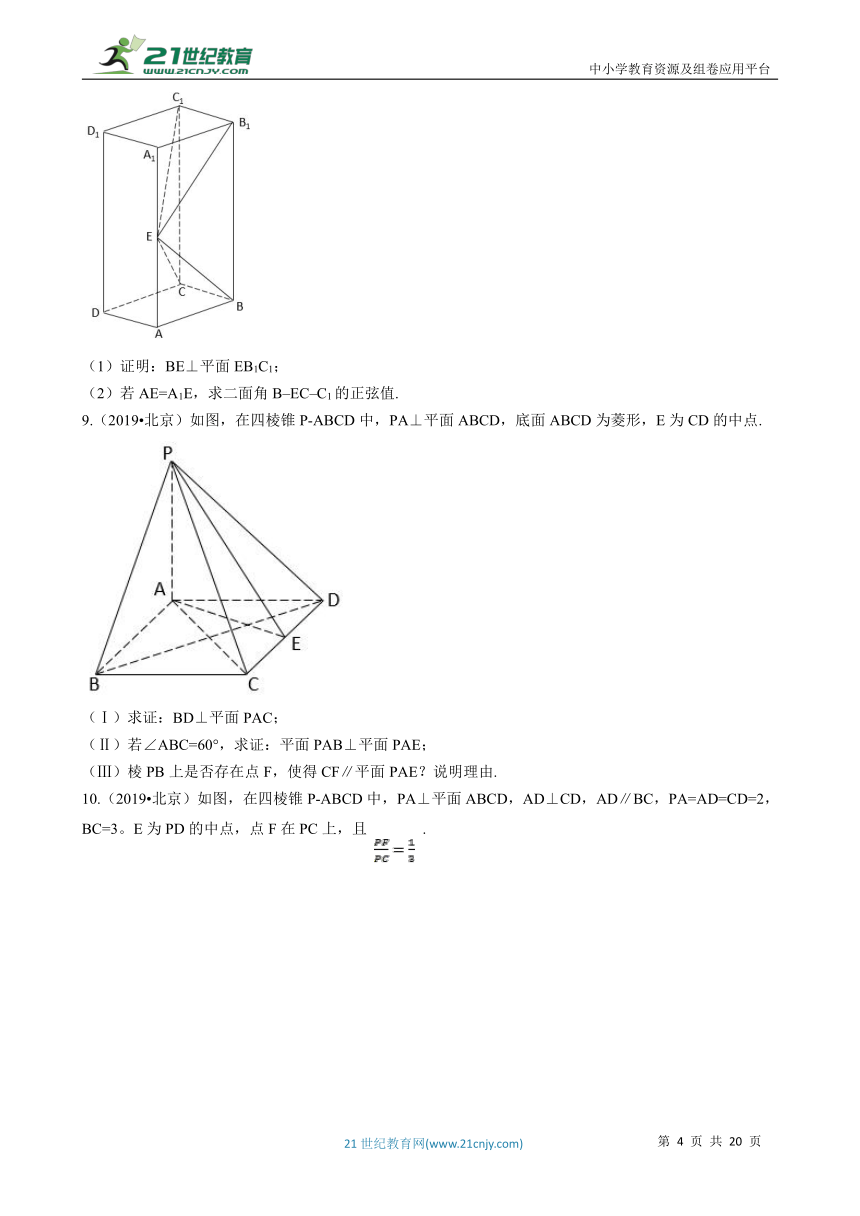
7.(2019?卷Ⅱ)如图,长方体 的底面 是正方形,点 在棱 上, 。
(1)证明: ;
(2)若 , ,求四棱锥 的体积。
8.(2019?卷Ⅱ)如图,长方体ABCD–A1B1C1D1的底面ABCD是正方形,点E在棱AA1上,BE⊥EC1.
?
(1)证明:BE⊥平面EB1C1;
(2)若AE=A1E,求二面角B–EC–C1的正弦值.
9.(2019?北京)如图,在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD为菱形,E为CD的中点.
(Ⅰ)求证:BD⊥平面PAC;
(Ⅱ)若∠ABC=60°,求证:平面PAB⊥平面PAE;
(Ⅲ)棱PB上是否存在点F,使得CF∥平面PAE?说明理由.
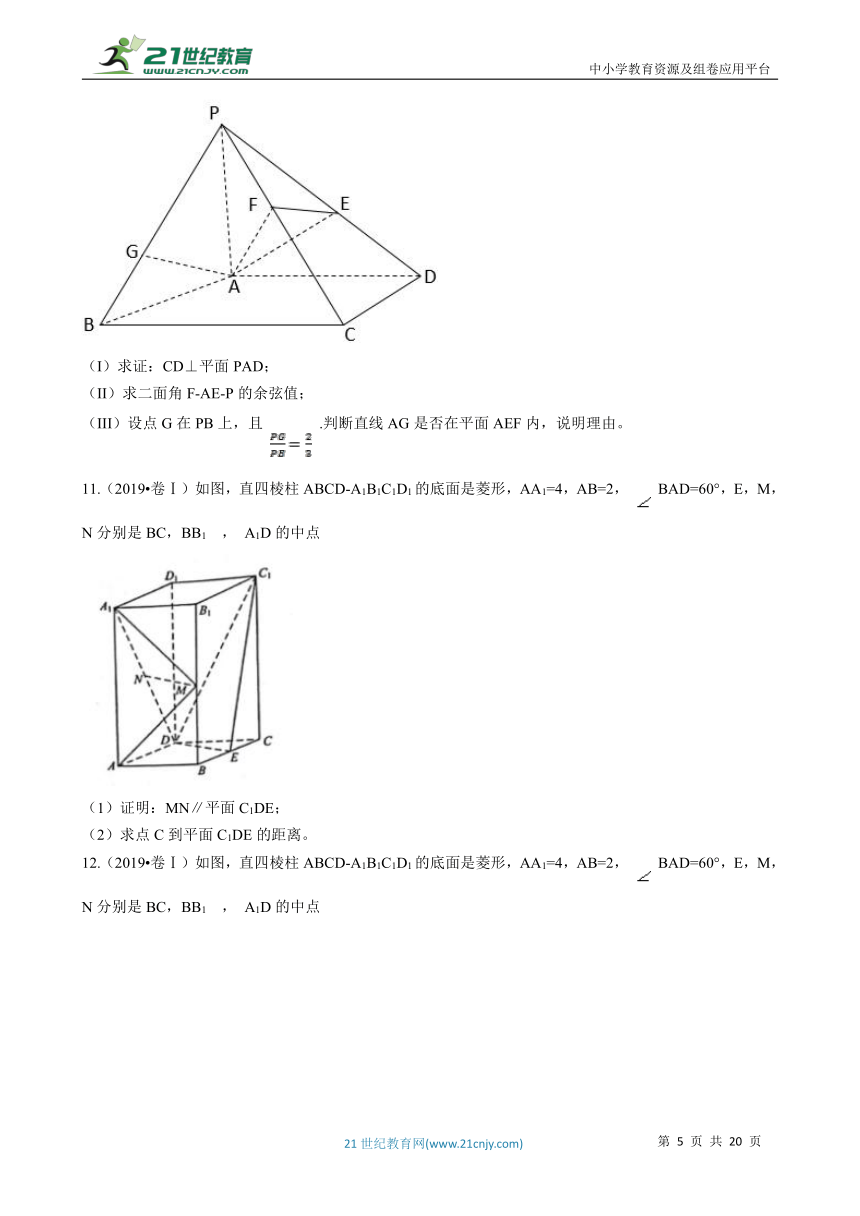
10.(2019?北京)如图,在四棱锥P-ABCD中,PA⊥平面ABCD,AD⊥CD,AD∥BC,PA=AD=CD=2,BC=3。E为PD的中点,点F在PC上,且 .
(I)求证:CD⊥平面PAD;
(II)求二面角F-AE-P的余弦值;
(III)设点G在PB上,且 .判断直线AG是否在平面AEF内,说明理由。
11.(2019?卷Ⅰ)如图,直四棱柱ABCD-A1B1C1D1的底面是菱形,AA1=4,AB=2, BAD=60°,E,M,N分别是BC,BB1 , A1D的中点
(1)证明:MN∥平面C1DE;
(2)求点C到平面C1DE的距离。
12.(2019?卷Ⅰ)如图,直四棱柱ABCD-A1B1C1D1的底面是菱形,AA1=4,AB=2, BAD=60°,E,M,N分别是BC,BB1 , A1D的中点
(1)证明:MN∥平面C1DE;
(2)求二面角A-MA1-N的正弦值。
答案解析部分
一、解答题
1.【答案】 (1)证明:因为D , E分别为BC , AC的中点,
所以ED∥AB.
在直三棱柱ABC-A1B1C1中,AB∥A1B1 ,
所以A1B1∥ED.
又因为ED?平面DEC1 , A1B1 平面DEC1 ,
所以A1B1∥平面DEC1. (2)解:因为AB=BC , E为AC的中点,所以BE⊥AC.
因为三棱柱ABC-A1B1C1是直棱柱,所以CC1⊥平面ABC.
又因为BE?平面ABC , 所以CC1⊥BE.
因为C1C?平面A1ACC1 , AC?平面A1ACC1 , C1C∩AC=C ,
所以BE⊥平面A1ACC1.
因为C1E?平面A1ACC1 , 所以BE⊥C1E.
【考点】直线与平面平行的判定,直线与平面垂直的判定
【解析】【分析】(1)利用直三棱柱的结构特征结合中点的性质,用中位线证出线线平行,从而证出线面平行。 (2)因为AB=BC , E为AC的中点,所以BE⊥AC , 再结合直三棱柱的结构特征证出线面垂直,再利用线面垂直的定义证出线线垂直。
2.【答案】 (1)连接A1E , 因为A1A=A1C , E是AC的中点,所以A1E⊥ AC.
又平面A1ACC1⊥平面ABC , A1E 平面A1ACC1 ,
平面A1ACC1∩平面ABC=AC ,
所以,A1E⊥ 平面ABC , 则A1E⊥ BC.
又因为A1F∥AB , ∠ABC=90°,故BC⊥A1F.
所以BC⊥平面A1EF.
因此EF⊥ BC. (2)取BC中点G , 连接EG , GF , 则EGFA1是平行四边形.
由于A1E⊥平面ABC , 故AE1⊥EG , 所以平行四边形EGFA1为矩形.
由(I)得BC⊥平面EGFA1 , 则平面A1BC⊥平面EGFA1 ,
所以EF在平面A1BC上的射影在直线A1G上.
连接A1G交EF于O , 则∠EOG是直线EF与平面A1BC所成的角(或其补角).
不妨设AC=4,则在Rt△A1EG中,A1E=2 ,EG= .
由于O为A1G的中点,故 ,
所以 .
因此,直线EF与平面A1BC所成角的余弦值是 .
方法二:
连接A1E , 因为A1A=A1C , E是AC的中点,所以A1E⊥AC.
又平面A1ACC1⊥平面ABC , A1E 平面A1ACC1 ,
平面A1ACC1∩平面ABC=AC , 所以,A1E⊥平面ABC.
如图,以点E为原点,分别以射线EC , EA1为y , z轴的正半轴,建立空间直角坐标系E–xyz.
不妨设AC=4,则
A1(0,0,2 ),B( ,1,0), , ,C(0,2,0).
因此, , .
由 得 .
【考点】直线与平面垂直的判定,直线与平面所成的角
【解析】【分析】(1)根据线面垂直的判定定理,证明线面垂直,即可得到线线垂直; (2) 通过线面垂直,找到直线与平面所成的角,结合余弦定理,求出相应的角即可.
3.【答案】 解:(Ⅰ)证明:连接 ,易知 , .又由 ,故 ,又因为 平面 , 平面 ,所以 平面 .
(Ⅱ)证明:取棱 的中点 ,连接 .依题意,得 ,又因为平面 平面 ,平面 平面 ,所以 平面 ,交 平面 ,故 .又已知 , ,所以 平面 .
(Ⅲ)解:连接 ,由(Ⅱ)中 平面 ,可知 为直线 与平面 所成的角,
因为 为等边三角形, 且 为 的中点,所以 .又 ,
在 中, .
所以,直线 与平面 所成角的正弦值为
【考点】直线与平面平行的判定,直线与平面垂直的判定,直线与平面所成的角
【解析】【分析】(Ⅰ)欲证 平面 ,根据直线与平面平行的判定定理可知只需证 与平面 内一直线平行,由三角形中位线可得 ,即可证得;
(Ⅱ))欲证 平面 ,根据直线与平面垂直的判定定理可知只需证 与平面 内两相交直线垂直,由平面 平面 , ,得出 平面 ,进而得出 ,再由 ,即可证得 平面 ;
(Ⅲ)连接 ,构造直角三角形 ,可知 为直线 与平面 所成的角,解直角三角形,求出 的大小,即可得出直线 与平面 所成的角。
4.【答案】 解:依题意,可以建立以 为原点,分别以 的方向为 轴, 轴, 轴正方向的空间直角坐标系(如图),
可得 , .设 ,则 .
(Ⅰ)证明:依题意, 是平面 的法向量,又 ,可得 ,又因为直线 平面 ,所以 平面 .
(Ⅱ)依题意, .
设 为平面 的法向量,则 即 不妨令 ,
可得 .因此有 .
所以,直线 与平面 所成角的正弦值为 .
(Ⅲ)设 为平面 的法向量,则 即
不妨令 ,可得 .
由题意,有 ,解得 .经检验,符合题意.
所以,线段 的长为
【考点】用向量证明平行,用空间向量求直线与平面的夹角,用空间向量求平面间的夹角
【解析】【分析】本题主要考查空间向量的应用,直线与平面平行判定定理、二面角、直线与平面所成的角等知识。
(Ⅰ)欲证 平面 ,需证出 与平面 的法向量垂直,由 是平面 的法向量,又 ,可得 ,进而得出 平面 ;
(Ⅱ)要求直线 与平面 所成角的正弦值,只要找出 与平面 的法向量所成的角的余弦值即可。
(Ⅲ)设出平面 的法向量 ,根据 求出 ,再根据 ,求出线段CF的长。
5.【答案】 (1)解:由已知得AD BE , CG BE , 所以AD CG , 故AD , CG确定一个平面,从而A , C , G , D四点共面.
由已知得AB BE , AB BC , 故AB 平面BCGE .
又因为AB 平面ABC , 所以平面ABC 平面BCGE . (2)取CG的中点M , 连结EM , DM.
因为AB//DE , AB 平面BCGE,所以DE 平面BCGE , 故DE CG.
由已知,四边形BCGE是菱形,且∠EBC=60°得EM CG , 故CG 平面DEM.
因此DM CG.
在 DEM中,DE=1,EM= ,故DM=2.
所以四边形ACGD的面积为4.
【考点】直线与平面垂直的判定,平面与平面垂直的判定
【解析】【分析】(1)由已知可证AD CG , 得到AD , CG确定一个平面,即可证明结论;(2)先作辅助线,可证DE 平面BCGE , 得DE CG , 又可证CG 平面DEM , 得DM CG , 利用勾股定理得到DM=2,即可求出四边形ACGD的面积.
6.【答案】 (1)解:由已知得AD BE,CG BE,所以AD CG,故AD,CG确定一个平面,从而A,C,G,D四点共面.
由已知得AB BE,AB BC,故AB 平面BCGE.
又因为AB 平面ABC,所以平面ABC 平面BCGE. (2)作EH BC,垂足为H.因为EH 平面BCGE,平面BCGE 平面ABC,所以EH 平面ABC.
由已知,菱形BCGE的边长为2,∠ EBC=60°,可求得BH=1,EH= .
以H为坐标原点, 的方向为x轴的正方向,建立如图所示的空间直角坐标系H–xyz,
则A(–1,1,0),C(1,0,0),G(2,0, ), =(1,0, ), =(2,–1,0).
设平面ACGD的法向量为 =(x,y,z),则
即
所以可取 =(3,6,– ).
又平面BCGE的法向量可取为 =(0,1,0),所以 .
因此二面角B–CG–A的大小为30°.
【考点】平面与平面垂直的判定,用空间向量求平面间的夹角
【解析】【分析】(1)由已知可证AD CG,得到AD,CG确定一个平面,即可证明结论;(2)先作辅助线,可证EH 平面ABC,再建立空间直角坐标系,求出平面ACGD与平面BCGE的法向量,代入向量的夹角公式,即可求出二面角B–CG–A的大小.
7.【答案】 (1)解:由已知得B1C1⊥平面ABB1A1 , BE 平面ABB1A1 ,
故 .
又 ,所以BE⊥平面 . (2)由(1)知∠BEB1=90°.由题设知Rt△ ABE≌ Rt△ A1B1E,所以 ,故AE=AB=3, .
作 ,垂足为F, 则EF⊥平面 ,且 .
所以,四棱锥 的体积 .
【考点】棱柱、棱锥、棱台的体积,直线与平面垂直的判定
【解析】【分析】(1)利用线面垂直的性质得出线线垂直,再由线面垂直的判定定理即可得证。(2)由三角形全等的出 ,进而得出边的关系,再结合题意作出辅助线,得出线线垂直从而得出线面垂直即可得出四棱锥的高线,再由四棱锥的体积公式代入数值求出结果即可。
8.【答案】 (1)解:由已知得, 平面 , 平面 ,
故 .
又 ,所以 平面 .
(2)由(1)知 .由题设知 ,所以 ,
故 , .
以 为坐标原点, 的方向为x轴正方向, 为单位长,建立如图所示的空间直角坐标系D-xyz, 则C(0,1,0),B(1,1,0), (0,1,2),E(1,0,1), , .
设平面EBC的法向量为 =(x,y,x),则
即
所以可取 = .
设平面 的法向量为 =(x,y,z),则
即
所以可取 =(1,1,0).
于是 .
所以,二面角 的正弦值为 .
【考点】直线与平面垂直的判定,与二面角有关的立体几何综合题
【解析】【分析】(1)根据题意由线面垂直的性质得出线线垂直,再由线线垂直的判定定理出线面垂直。(2)建立空间直角坐标系,分别求出各个点的坐标以及对应的向量的坐标,构造出法向量n由向量垂直的数量积为零,求出法向量n,同理求出平面 的法向量m,则两个平面垂直即为两个法向量垂直,利用数量积的运算公式即可求出两个法向量所成角的余弦值,从而求出该角的正弦值即为二面角 的正弦值。
9.【答案】 (Ⅰ)证明:因为ABCD为菱形,所以 ,
又因为 ,所以 ,而 ,
故 ;
(Ⅱ)因为 ,所以 ,故 为等边三角形,
而E为CD 的中点,故 ,所以 ,
又因为 ,所以 ,
因为 ,所以 ,
又因为 ,所以 ;
(Ⅲ)存在这样的F,当F为PB的中点时, ;
取AB的中点G,连接CF、CG和FG,
因为G为AB中点,所以AE与GC平行且相等,
故四边形AGCE为平行四边形,所以 ,故
在三角形BAP中,F、G分别为BP、BA的中点,所以 ,
故 ,因为GC和FG均在平面CFG内,且 ,
所以 ,故 .
【考点】直线与平面平行的判定,直线与平面垂直的判定,平面与平面垂直的判定
【解析】【分析】(Ⅰ)根据线面垂直的判定定理,证明直线与平面内两条相交直线垂直即可;
(Ⅱ)根据面面垂直的判定定理,证明直线与平面垂直,即可得到面面垂直;
(Ⅲ)根据面面平行的判定定理,证明面面平行,即可说明两平面没有公共点,因此,一个平面内任意一条直线与另一平面均无公共点,即可说明线面平行.
10.【答案】 (I)证明:因为PA 平面ABCD,所以PA CD,
又因为CD AD, ,所以CD 平面PAD;
(II)过A作AM BC交BC于M,
以A为原点,AM,AD,AP所在直线为x,y,z轴建立空间直角坐标系,
由于PA=AD=CD=2,BC=3,E为PD的中点, ,
A(0,0,0),C(2,2,0),D(0,2,0),P(0,0,2), ,
E(0,1,1),M(2,0,0)
由已知,平面AEP的法向量为 ,
设平面AEF的法向量为 ,且 ,
由 得 令z=-1,则 ,
设二面角F-AE-P的夹角为 ,
则 ,
而二面角F-AE-P为锐二面角,故其余弦值为 ;
(III)设点B(2,-1,0),由于 ,且 ,
则 ,
所以 ,
而平面AEF的法向量 ,
且 ,所以 ,而 平面AEF,
所以AG在平面AEF内.
【考点】直线与平面垂直的判定,二面角的平面角及求法
【解析】【分析】(I)根据线面垂直的判定定理,证明线线垂直,即可得到线面垂直;
(II)建立空间直角坐标系,表示点的坐标,写出相应的向量,求出平面的法向量,结合空间向量的数量积运算,即可求出二面角的余弦值;
(III)根据空间向量,证明法向量与直线的方向向量垂直,再根据点在平面内,即可证明直线在平面内.
11.【答案】 (1)解:连结 .因为M , E分别为 的中点,所以 ,且 .又因为N为 的中点,所以 .
由题设知 ,可得 ,故 ,因此四边形MNDE为平行四边形, .又 平面 ,所以MN∥平面 .
(2)过C作C1E的垂线,垂足为H.
由已知可得 , ,所以DE⊥平面 ,故DE⊥CH.
从而CH⊥平面 ,故CH的长即为C到平面 的距离,
由已知可得CE=1,C1C=4,所以 ,故 .
从而点C到平面 的距离为 .
【考点】棱柱、棱锥、棱台的体积,直线与平面平行的判定
【解析】【分析】(1)利用直四棱柱的结构特征结合已知条件,用中点作中位线证线线平行,再利用线线相等结合平行四边形的定义证出四边形MNDE为平行四边形,再利用平行四边形的定义证出另一组线线平行,从而用线线平行结合线面平行的判定定理证出线面平行。(2)利用直四棱柱的结构特征结合已知条件,用线面垂直的定义证出线线垂直,再利用线面垂直结合线面垂直的判定定理证出线面垂直,从而推出CH的长即为C到平面 的距离,由已知可得CE=1,C1C=4,所以 ,故 从而点C到平面 的距离为 .
12.【答案】 (1)解:连结 .因为M , E分别为 的中点,所以 ,且 .又因为N为 的中点,所以 .
由题设知 ,可得 ,故 ,因此四边形MNDE为平行四边形, .又 平面 ,所以MN∥平面 .
(2)解:建立空间直角坐标系,点N在底面投影为点F,
设平面 的法向量为
由 取 得其中一个法向量
易知平面 的一个法向量为
所以二面角 的正弦值为
【考点】直线与平面平行的判定,二面角的平面角及求法
【解析】【分析】(1)利用直四棱柱的结构特征结合已知条件,用中点作中位线证线线平行,再利用线线相等结合平行四边形的定义证出四边形MNDE为平行四边形,再利用平行四边形的定义证出另一组线线平行,从而用线线平行结合线面平行的判定定理证出线面平行。(2)利用直四棱柱的结构特征结合已知条件找出二面角的平面角,再利用空间向量的方法求出二面角的平面角的正弦值。
一、解答题
1.如图,在直三棱柱ABC-A1B1C1中,D , E分别为BC , AC的中点,AB=BC .
求证:
(1)A1B1∥平面DEC1;
(2)BE⊥C1E .
2.(2019?浙江)如图,已知三棱柱ABC-A1B1C1 , 平面A1AC1C⊥平面ABC,∠ABC=90°.∠BAC=30°,A1A=A1C=AC,E,F分别是AC,A1B1的中点
?
(1)证明:EF⊥BC
(2)求直线EF与平面A1BC所成角的余弦值.
3.(2019?天津)如图,在四棱锥 中,底面 为平行四边形, 为等边三角形,平面 平面 , , ,
(Ⅰ)设 分别为 的中点,求证: 平面 ;
(Ⅱ)求证: 平面 ;
(Ⅲ)求直线 与平面 所成角的正弦值.
4.(2019?天津)如图, 平面 , , .
(Ⅰ)求证: 平面 ;
(Ⅱ)求直线 与平面 所成角的正弦值;
(Ⅲ)若二面角 的余弦值为 ,求线段 的长.
5.(2019?全国Ⅲ)图1是由矩形ADEB、 ABC和菱形BFGC组成的一个平面图形,其中AB=1,BE=BF=2,∠FBC=60°.将其沿AB , BC折起使得BE与BF重合,连结DG , 如图2.
(1)证明图2中的A , C , G , D四点共面,且平面ABC⊥平面BCGE;
(2)求图2中的四边形ACGD的面积.
6.(2019?全国Ⅲ)图1是由矩形ADEB、Rt△ABC和菱形BFCC组成的一个平面图形,其中AB=1,BE=BF=2,∠FBC=60°,将其沿AB,BC折起使得BE与BF重合,连结DC,如题2.
(1)证明:图2中的A,C,G,D四点共面,且平面ABC⊥平面BCGE;
(2)求图2中的二面角B-CG-A的大小.
7.(2019?卷Ⅱ)如图,长方体 的底面 是正方形,点 在棱 上, 。
(1)证明: ;
(2)若 , ,求四棱锥 的体积。
8.(2019?卷Ⅱ)如图,长方体ABCD–A1B1C1D1的底面ABCD是正方形,点E在棱AA1上,BE⊥EC1.
?
(1)证明:BE⊥平面EB1C1;
(2)若AE=A1E,求二面角B–EC–C1的正弦值.
9.(2019?北京)如图,在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD为菱形,E为CD的中点.
(Ⅰ)求证:BD⊥平面PAC;
(Ⅱ)若∠ABC=60°,求证:平面PAB⊥平面PAE;
(Ⅲ)棱PB上是否存在点F,使得CF∥平面PAE?说明理由.
10.(2019?北京)如图,在四棱锥P-ABCD中,PA⊥平面ABCD,AD⊥CD,AD∥BC,PA=AD=CD=2,BC=3。E为PD的中点,点F在PC上,且 .
(I)求证:CD⊥平面PAD;
(II)求二面角F-AE-P的余弦值;
(III)设点G在PB上,且 .判断直线AG是否在平面AEF内,说明理由。
11.(2019?卷Ⅰ)如图,直四棱柱ABCD-A1B1C1D1的底面是菱形,AA1=4,AB=2, BAD=60°,E,M,N分别是BC,BB1 , A1D的中点
(1)证明:MN∥平面C1DE;
(2)求点C到平面C1DE的距离。
12.(2019?卷Ⅰ)如图,直四棱柱ABCD-A1B1C1D1的底面是菱形,AA1=4,AB=2, BAD=60°,E,M,N分别是BC,BB1 , A1D的中点
(1)证明:MN∥平面C1DE;
(2)求二面角A-MA1-N的正弦值。
答案解析部分
一、解答题
1.【答案】 (1)证明:因为D , E分别为BC , AC的中点,
所以ED∥AB.
在直三棱柱ABC-A1B1C1中,AB∥A1B1 ,
所以A1B1∥ED.
又因为ED?平面DEC1 , A1B1 平面DEC1 ,
所以A1B1∥平面DEC1. (2)解:因为AB=BC , E为AC的中点,所以BE⊥AC.
因为三棱柱ABC-A1B1C1是直棱柱,所以CC1⊥平面ABC.
又因为BE?平面ABC , 所以CC1⊥BE.
因为C1C?平面A1ACC1 , AC?平面A1ACC1 , C1C∩AC=C ,
所以BE⊥平面A1ACC1.
因为C1E?平面A1ACC1 , 所以BE⊥C1E.
【考点】直线与平面平行的判定,直线与平面垂直的判定
【解析】【分析】(1)利用直三棱柱的结构特征结合中点的性质,用中位线证出线线平行,从而证出线面平行。 (2)因为AB=BC , E为AC的中点,所以BE⊥AC , 再结合直三棱柱的结构特征证出线面垂直,再利用线面垂直的定义证出线线垂直。
2.【答案】 (1)连接A1E , 因为A1A=A1C , E是AC的中点,所以A1E⊥ AC.
又平面A1ACC1⊥平面ABC , A1E 平面A1ACC1 ,
平面A1ACC1∩平面ABC=AC ,
所以,A1E⊥ 平面ABC , 则A1E⊥ BC.
又因为A1F∥AB , ∠ABC=90°,故BC⊥A1F.
所以BC⊥平面A1EF.
因此EF⊥ BC. (2)取BC中点G , 连接EG , GF , 则EGFA1是平行四边形.
由于A1E⊥平面ABC , 故AE1⊥EG , 所以平行四边形EGFA1为矩形.
由(I)得BC⊥平面EGFA1 , 则平面A1BC⊥平面EGFA1 ,
所以EF在平面A1BC上的射影在直线A1G上.
连接A1G交EF于O , 则∠EOG是直线EF与平面A1BC所成的角(或其补角).
不妨设AC=4,则在Rt△A1EG中,A1E=2 ,EG= .
由于O为A1G的中点,故 ,
所以 .
因此,直线EF与平面A1BC所成角的余弦值是 .
方法二:
连接A1E , 因为A1A=A1C , E是AC的中点,所以A1E⊥AC.
又平面A1ACC1⊥平面ABC , A1E 平面A1ACC1 ,
平面A1ACC1∩平面ABC=AC , 所以,A1E⊥平面ABC.
如图,以点E为原点,分别以射线EC , EA1为y , z轴的正半轴,建立空间直角坐标系E–xyz.
不妨设AC=4,则
A1(0,0,2 ),B( ,1,0), , ,C(0,2,0).
因此, , .
由 得 .
【考点】直线与平面垂直的判定,直线与平面所成的角
【解析】【分析】(1)根据线面垂直的判定定理,证明线面垂直,即可得到线线垂直; (2) 通过线面垂直,找到直线与平面所成的角,结合余弦定理,求出相应的角即可.
3.【答案】 解:(Ⅰ)证明:连接 ,易知 , .又由 ,故 ,又因为 平面 , 平面 ,所以 平面 .
(Ⅱ)证明:取棱 的中点 ,连接 .依题意,得 ,又因为平面 平面 ,平面 平面 ,所以 平面 ,交 平面 ,故 .又已知 , ,所以 平面 .
(Ⅲ)解:连接 ,由(Ⅱ)中 平面 ,可知 为直线 与平面 所成的角,
因为 为等边三角形, 且 为 的中点,所以 .又 ,
在 中, .
所以,直线 与平面 所成角的正弦值为
【考点】直线与平面平行的判定,直线与平面垂直的判定,直线与平面所成的角
【解析】【分析】(Ⅰ)欲证 平面 ,根据直线与平面平行的判定定理可知只需证 与平面 内一直线平行,由三角形中位线可得 ,即可证得;
(Ⅱ))欲证 平面 ,根据直线与平面垂直的判定定理可知只需证 与平面 内两相交直线垂直,由平面 平面 , ,得出 平面 ,进而得出 ,再由 ,即可证得 平面 ;
(Ⅲ)连接 ,构造直角三角形 ,可知 为直线 与平面 所成的角,解直角三角形,求出 的大小,即可得出直线 与平面 所成的角。
4.【答案】 解:依题意,可以建立以 为原点,分别以 的方向为 轴, 轴, 轴正方向的空间直角坐标系(如图),
可得 , .设 ,则 .
(Ⅰ)证明:依题意, 是平面 的法向量,又 ,可得 ,又因为直线 平面 ,所以 平面 .
(Ⅱ)依题意, .
设 为平面 的法向量,则 即 不妨令 ,
可得 .因此有 .
所以,直线 与平面 所成角的正弦值为 .
(Ⅲ)设 为平面 的法向量,则 即
不妨令 ,可得 .
由题意,有 ,解得 .经检验,符合题意.
所以,线段 的长为
【考点】用向量证明平行,用空间向量求直线与平面的夹角,用空间向量求平面间的夹角
【解析】【分析】本题主要考查空间向量的应用,直线与平面平行判定定理、二面角、直线与平面所成的角等知识。
(Ⅰ)欲证 平面 ,需证出 与平面 的法向量垂直,由 是平面 的法向量,又 ,可得 ,进而得出 平面 ;
(Ⅱ)要求直线 与平面 所成角的正弦值,只要找出 与平面 的法向量所成的角的余弦值即可。
(Ⅲ)设出平面 的法向量 ,根据 求出 ,再根据 ,求出线段CF的长。
5.【答案】 (1)解:由已知得AD BE , CG BE , 所以AD CG , 故AD , CG确定一个平面,从而A , C , G , D四点共面.
由已知得AB BE , AB BC , 故AB 平面BCGE .
又因为AB 平面ABC , 所以平面ABC 平面BCGE . (2)取CG的中点M , 连结EM , DM.
因为AB//DE , AB 平面BCGE,所以DE 平面BCGE , 故DE CG.
由已知,四边形BCGE是菱形,且∠EBC=60°得EM CG , 故CG 平面DEM.
因此DM CG.
在 DEM中,DE=1,EM= ,故DM=2.
所以四边形ACGD的面积为4.
【考点】直线与平面垂直的判定,平面与平面垂直的判定
【解析】【分析】(1)由已知可证AD CG , 得到AD , CG确定一个平面,即可证明结论;(2)先作辅助线,可证DE 平面BCGE , 得DE CG , 又可证CG 平面DEM , 得DM CG , 利用勾股定理得到DM=2,即可求出四边形ACGD的面积.
6.【答案】 (1)解:由已知得AD BE,CG BE,所以AD CG,故AD,CG确定一个平面,从而A,C,G,D四点共面.
由已知得AB BE,AB BC,故AB 平面BCGE.
又因为AB 平面ABC,所以平面ABC 平面BCGE. (2)作EH BC,垂足为H.因为EH 平面BCGE,平面BCGE 平面ABC,所以EH 平面ABC.
由已知,菱形BCGE的边长为2,∠ EBC=60°,可求得BH=1,EH= .
以H为坐标原点, 的方向为x轴的正方向,建立如图所示的空间直角坐标系H–xyz,
则A(–1,1,0),C(1,0,0),G(2,0, ), =(1,0, ), =(2,–1,0).
设平面ACGD的法向量为 =(x,y,z),则
即
所以可取 =(3,6,– ).
又平面BCGE的法向量可取为 =(0,1,0),所以 .
因此二面角B–CG–A的大小为30°.
【考点】平面与平面垂直的判定,用空间向量求平面间的夹角
【解析】【分析】(1)由已知可证AD CG,得到AD,CG确定一个平面,即可证明结论;(2)先作辅助线,可证EH 平面ABC,再建立空间直角坐标系,求出平面ACGD与平面BCGE的法向量,代入向量的夹角公式,即可求出二面角B–CG–A的大小.
7.【答案】 (1)解:由已知得B1C1⊥平面ABB1A1 , BE 平面ABB1A1 ,
故 .
又 ,所以BE⊥平面 . (2)由(1)知∠BEB1=90°.由题设知Rt△ ABE≌ Rt△ A1B1E,所以 ,故AE=AB=3, .
作 ,垂足为F, 则EF⊥平面 ,且 .
所以,四棱锥 的体积 .
【考点】棱柱、棱锥、棱台的体积,直线与平面垂直的判定
【解析】【分析】(1)利用线面垂直的性质得出线线垂直,再由线面垂直的判定定理即可得证。(2)由三角形全等的出 ,进而得出边的关系,再结合题意作出辅助线,得出线线垂直从而得出线面垂直即可得出四棱锥的高线,再由四棱锥的体积公式代入数值求出结果即可。
8.【答案】 (1)解:由已知得, 平面 , 平面 ,
故 .
又 ,所以 平面 .
(2)由(1)知 .由题设知 ,所以 ,
故 , .
以 为坐标原点, 的方向为x轴正方向, 为单位长,建立如图所示的空间直角坐标系D-xyz, 则C(0,1,0),B(1,1,0), (0,1,2),E(1,0,1), , .
设平面EBC的法向量为 =(x,y,x),则
即
所以可取 = .
设平面 的法向量为 =(x,y,z),则
即
所以可取 =(1,1,0).
于是 .
所以,二面角 的正弦值为 .
【考点】直线与平面垂直的判定,与二面角有关的立体几何综合题
【解析】【分析】(1)根据题意由线面垂直的性质得出线线垂直,再由线线垂直的判定定理出线面垂直。(2)建立空间直角坐标系,分别求出各个点的坐标以及对应的向量的坐标,构造出法向量n由向量垂直的数量积为零,求出法向量n,同理求出平面 的法向量m,则两个平面垂直即为两个法向量垂直,利用数量积的运算公式即可求出两个法向量所成角的余弦值,从而求出该角的正弦值即为二面角 的正弦值。
9.【答案】 (Ⅰ)证明:因为ABCD为菱形,所以 ,
又因为 ,所以 ,而 ,
故 ;
(Ⅱ)因为 ,所以 ,故 为等边三角形,
而E为CD 的中点,故 ,所以 ,
又因为 ,所以 ,
因为 ,所以 ,
又因为 ,所以 ;
(Ⅲ)存在这样的F,当F为PB的中点时, ;
取AB的中点G,连接CF、CG和FG,
因为G为AB中点,所以AE与GC平行且相等,
故四边形AGCE为平行四边形,所以 ,故
在三角形BAP中,F、G分别为BP、BA的中点,所以 ,
故 ,因为GC和FG均在平面CFG内,且 ,
所以 ,故 .
【考点】直线与平面平行的判定,直线与平面垂直的判定,平面与平面垂直的判定
【解析】【分析】(Ⅰ)根据线面垂直的判定定理,证明直线与平面内两条相交直线垂直即可;
(Ⅱ)根据面面垂直的判定定理,证明直线与平面垂直,即可得到面面垂直;
(Ⅲ)根据面面平行的判定定理,证明面面平行,即可说明两平面没有公共点,因此,一个平面内任意一条直线与另一平面均无公共点,即可说明线面平行.
10.【答案】 (I)证明:因为PA 平面ABCD,所以PA CD,
又因为CD AD, ,所以CD 平面PAD;
(II)过A作AM BC交BC于M,
以A为原点,AM,AD,AP所在直线为x,y,z轴建立空间直角坐标系,
由于PA=AD=CD=2,BC=3,E为PD的中点, ,
A(0,0,0),C(2,2,0),D(0,2,0),P(0,0,2), ,
E(0,1,1),M(2,0,0)
由已知,平面AEP的法向量为 ,
设平面AEF的法向量为 ,且 ,
由 得 令z=-1,则 ,
设二面角F-AE-P的夹角为 ,
则 ,
而二面角F-AE-P为锐二面角,故其余弦值为 ;
(III)设点B(2,-1,0),由于 ,且 ,
则 ,
所以 ,
而平面AEF的法向量 ,
且 ,所以 ,而 平面AEF,
所以AG在平面AEF内.
【考点】直线与平面垂直的判定,二面角的平面角及求法
【解析】【分析】(I)根据线面垂直的判定定理,证明线线垂直,即可得到线面垂直;
(II)建立空间直角坐标系,表示点的坐标,写出相应的向量,求出平面的法向量,结合空间向量的数量积运算,即可求出二面角的余弦值;
(III)根据空间向量,证明法向量与直线的方向向量垂直,再根据点在平面内,即可证明直线在平面内.
11.【答案】 (1)解:连结 .因为M , E分别为 的中点,所以 ,且 .又因为N为 的中点,所以 .
由题设知 ,可得 ,故 ,因此四边形MNDE为平行四边形, .又 平面 ,所以MN∥平面 .
(2)过C作C1E的垂线,垂足为H.
由已知可得 , ,所以DE⊥平面 ,故DE⊥CH.
从而CH⊥平面 ,故CH的长即为C到平面 的距离,
由已知可得CE=1,C1C=4,所以 ,故 .
从而点C到平面 的距离为 .
【考点】棱柱、棱锥、棱台的体积,直线与平面平行的判定
【解析】【分析】(1)利用直四棱柱的结构特征结合已知条件,用中点作中位线证线线平行,再利用线线相等结合平行四边形的定义证出四边形MNDE为平行四边形,再利用平行四边形的定义证出另一组线线平行,从而用线线平行结合线面平行的判定定理证出线面平行。(2)利用直四棱柱的结构特征结合已知条件,用线面垂直的定义证出线线垂直,再利用线面垂直结合线面垂直的判定定理证出线面垂直,从而推出CH的长即为C到平面 的距离,由已知可得CE=1,C1C=4,所以 ,故 从而点C到平面 的距离为 .
12.【答案】 (1)解:连结 .因为M , E分别为 的中点,所以 ,且 .又因为N为 的中点,所以 .
由题设知 ,可得 ,故 ,因此四边形MNDE为平行四边形, .又 平面 ,所以MN∥平面 .
(2)解:建立空间直角坐标系,点N在底面投影为点F,
设平面 的法向量为
由 取 得其中一个法向量
易知平面 的一个法向量为
所以二面角 的正弦值为
【考点】直线与平面平行的判定,二面角的平面角及求法
【解析】【分析】(1)利用直四棱柱的结构特征结合已知条件,用中点作中位线证线线平行,再利用线线相等结合平行四边形的定义证出四边形MNDE为平行四边形,再利用平行四边形的定义证出另一组线线平行,从而用线线平行结合线面平行的判定定理证出线面平行。(2)利用直四棱柱的结构特征结合已知条件找出二面角的平面角,再利用空间向量的方法求出二面角的平面角的正弦值。
同课章节目录
