1.1 探索勾股定理 同步练习(解析版)
文档属性
| 名称 | 1.1 探索勾股定理 同步练习(解析版) |  | |
| 格式 | zip | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-09-25 18:47:10 | ||
图片预览



文档简介
初中数学北师大版八年级上学期 第一章 1.1 探索勾股定理
一、单选题
1.下列三条线段能构成直角三角形的是( ??)
A.?6, 7, 8????????????????????????????????B.?2, 3, 4????????????????????????????????C.?3, 4, 6????????????????????????????????D.?6,8, 10
2.在直线l上有三个正方形m、q、n,若m、q的面积分别为5和11,则n的面积( ??)
A.?4??????????????????????????????????????????
B.?6??????????????????????????????????????????
C.?16??????????????????????????????????????????
D.?55
3.将一根长24cm的筷子置于底面直径为5cm,高为12cm的圆柱水杯中,设筷子露在杯子外面的长度为h,则h的取值范围是( ??) 21教育网
A.?12cm≤h≤19cm?????????????
B.?12cm≤h≤13cm?????????????
C.?11cm≤h≤12cm?????????????
D.?5cm≤h≤12cm
4.如图,在矩形ABCD中,AB=6,BC=8,点E是BC边上一点,将△ABE沿AE折叠,使点B落在点F处,连结CF,当△CEF为直角三角形时,BE的长是( ??) 21cnjy.com
A.?4????????????????????????????????????????
B.?3???????????????????????????????????????
C.?4或8????????????????????????????????????????
D.?3或6
5.如图,在边长为1个单位长度的小正方形组成的网格中,点A、B都是格点,则线段AB的长度为( ??)
A.?5???????????????????????????????????????????
B.?6???????????????????????????????????????????
C.?7???????????????????????????????????????????
D.?25
二、填空题
6.公元3世纪初,中国古代数学家赵爽注《周髀算经》时,创造了“赵爽弦图”.如图,设勾 ,弦 ,则小正方形ABCD的面积是________. 21·cn·jy·com
7.如图,在 中, ,若 边上的中线 垂直相交于 点,则 ________.
8.如图,点D、E分别是直角△ABC的边AB和BC的点,将△BDE沿DE翻折到△ADE,若∠C=90°,AC=2 ,BC=8,则DE的长为________; www.21-cn-jy.com
三、解答题
9.A,B两个居民楼在公路同侧,它们离公路的距离分别为AE=200米,BF=70米,它们的水平距离EF=390米.现欲在公路旁建一个超市P,使超市到两居民楼的距离相等,则超市应建何处?为什么?
10.如图,BC=3cm,AB=4cm,AF=12cm,且∠B=∠FAC=90°,求正方形CDEF的面积.
11.铁路上A,B两站(视为直线上的两点)相距50km,C,D为两村庄(视为两个点),DA⊥AB于点A,CB⊥AB于点B(如图).已知DA=20km,CB=10km,现在要在铁路AB上建一个土特产收购站E,使得C,D两村庄到收购站E的直线距离相等,请你设计出收购站的位置,并计算出收购站E到A站的距离. 2·1·c·n·j·y
四、综合题
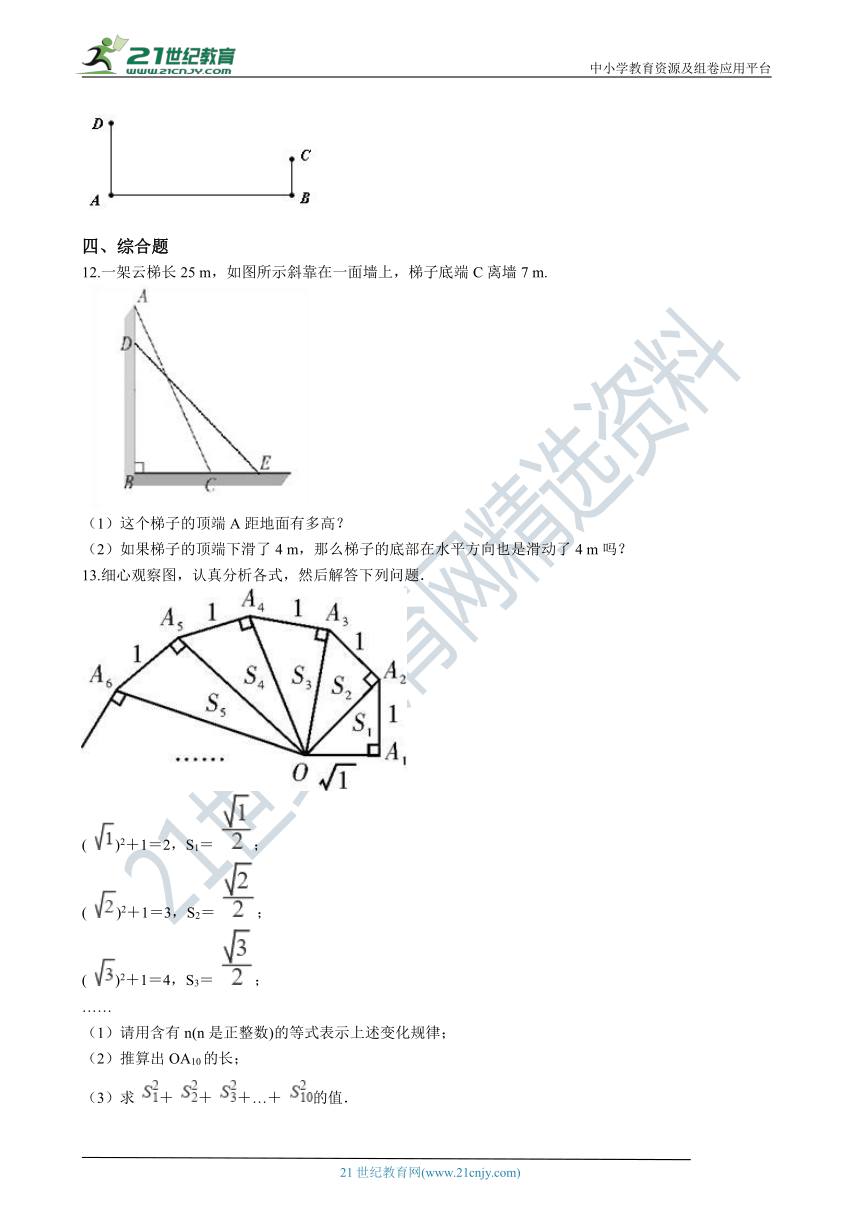
12.一架云梯长25 m,如图所示斜靠在一面墙上,梯子底端C离墙7 m.
(1)这个梯子的顶端A距地面有多高?
(2)如果梯子的顶端下滑了4 m,那么梯子的底部在水平方向也是滑动了4 m吗?
13.细心观察图,认真分析各式,然后解答下列问题.
( )2+1=2,S1= ;
( )2+1=3,S2= ;
( )2+1=4,S3= ;
……
(1)请用含有n(n是正整数)的等式表示上述变化规律;
(2)推算出OA10的长;
(3)求 + + +…+ 的值.
答案解析部分
一、单选题
1. D
解析:A、最大边82=64<62+72=85, 为锐角三角形,A不符合题意; B、最大边42=16>32+22=13, 为钝角三角形,B不符合题意; C、最大边62=36>32+42=25, 为钝角三角形,C不符合题意; C、最大边102=100=62+82=100, 为直角三角形,D不符合题意; 故答案为:D 【分析】先找出最大边,然后根据勾股定理分析判断,最大边的平方小于另外两边的平方和是锐角三角形,等于另外两边的平方和是直角三角形,大于另外两边的平方和是钝角三角形。育·网】
2. C
解析: ∵∠ACB+∠ECD=∠ACB+∠BAC=90°, ∴∠ABC=∠DEC,∠ACB=∠CDE,AC=CD, ∴△ACB≌△△DCE(AAS), ∴AB=CE,BC=DE, 由勾股定理可得,AC2=AB2+BC2=AB2+DE2 Sn=Sm+Sq=11+5=16. n的面积为16 21·世纪*教育网
故答案为:C.
【分析】利用全等三角形判定定理证明,再利用勾股定理求得线段的关系,得到面积。
3. C
解析: h最大时为筷子与杯底垂直时,h=12cm 最小时为筷子与杯底和杯高形成直角三角形时,AB= h=24-13=11cm, ∴11cm≤h≤12cm. www-2-1-cnjy-com
故答案为:C.
【分析】根据题意,找到h最小、最大值的情况,利用勾股定理解答。
4. D
解析:(1)当∠EFC=90°时, ∵∠AFE=∠ABE=90°, ∴∠AFE+∠EFC=180°, ∴A、F、C在同一条直线上, ∴AF=AB=6, ∴FC=AC-AF=10-6=4, 设BE=x, 则EF=x,EC=BC-BE=8-x, 由勾股定理得:EF2+FC2=EC2 , 即x2+42=(8-x)2, ∴x=3,即EF=3; 2)当点F在AD上时, A、F、D在同一条直线上, 这时四边形ABED是矩形, ∵△AFE是由△ABE折叠而得, ∴AF=AB=6, ∴BE=AF=6. 故答案为:D.21世纪教育网版权所有
【分析】△CEF为直角三角形有两种情况,即F在AC上时,或F在AD上时,分别利用折叠图形的特点找出相关相等的线段,设未知数,利用勾股定理列式即可解决。21*cnjy*com
5. A
解析:根据图形,利用勾股定理可得: ,故答案为:A.
【分析】利用方格纸的特点可知:AB是两直角边分别为3与4的直角三角形的斜边,利用勾股定理即可求出AB的长。【来源:21cnj*y.co*m】
二、填空题
6. 4
解析:∵勾 ,弦 ,
∴股b= ,
∴小正方形的边长= ,
∴小正方形的面积
故答案为:4 【分析】根据勾股定理计算得到b的长度,即可得到小正方形的边长计算其面积即可。
7.
解析:∵AD、BE分别为BC,AC的中线, ∴BD=BC=4,AE=AC=3, ∵点O是△ABC的重心, ∴AO=2OD,BO=2OE, ∵BE⊥AD, ∴∠AOE=∠BOD=90°, ∴AO2+OE2=AE2=9,BO2+OD2=BD2=16, ∴AO2+BO2=9①,BO2+OA2=16②, ①+②得AO2+OB2=25, ∴AO2+OB2=20, ∵AO2+OB2=AB2 , ∴AB=. 故答案为:. 【分析】根据三角形的中线,可得BD=BC=4,AE=AC=3,AO=2OD,BO=2OE.利用勾股定理可得AO2+OE2=AE2=9,BO2+OD2=BD2=16,从而可得AO2+BO2=9①,BO2+OA2=16②,两等式相加可得AO2+OB2=20,从而可求出AB的长.【出处:21教育名师】
8.
解析:∵在直角三角形ABC中,AC=2 ,BC=8
∴ =
故BD=
∵△BDE沿DE翻折到△ADE
∴BE=AE
所以CE=BC-BE=8-BE
在直角三角形△ABE中
即
解得AE=
故CE=
在直角三角形BDE中
= 【分析】先根据勾股定理求出AB的长,根据点D是AB的中点求出BD的长,根据翻折的性质求出CE=BC-BE=8-BE,然后在直角三角形△ABE中根据勾股定理列出关于AE的方程求出AE,进而求出CE,再根据勾股定理求出DE即可.2-1-c-n-j-y
三、解答题
9.解:设 米,则 米,由题意得: 解得: .故:超市应建在距离E处150米的位置. 【版权所有:21教育】
解析:根据勾股定理由题意可知AP=BP,因此设EP=x表示出PF,然后根据AP2=BP2建立关于x的方程,求解即可。21教育名师原创作品
10.解:∵∠B=90°, ∴AB2+BC2=AC2 , ∵AB=4,BC=3, ∴AC=5 ∵∠FAC=90°, ∴AC2+AF2=CF2 , ∵AC=5,AF =12, ∴CF=13 ∵S正方形CDEF=CF2 ∴S正方形CDEF=169。
解析:由题意可知,ΔABC与ΔACF都是直角三角形,由勾股定理可以分别求出AC与CF的长,正方形CDEF的面积等于边长的平方,即CF的平方,即可求得正方形CDEF的面积。
11.解: 连接DE,CE,设AE=x km,则BE=(50-x) km , 在Rt△ADE中, , ∴ 在Rt△BCE中, ?, ∴CE2=102+(50-x)2 , 又DE=CE, ∴202+x2=102+(50-x)2 , 解得x=22 ∴收购站E到A站的距离为22km。
解析:根据题意,作线段CD的垂直平分线交AB于点E,连接DE、CE。设AE=x km,则BE=(50-x) km ,在Rt△ADE和Rt△BCE中,用勾股定理表示出DE和CE,再根据等量关系DE=CE列方程求解即可。
四、综合题
12. (1)由题意得:AC=25米,BC=7米,
AB= =24(米),
答:这个梯子的顶端距地面有24米; (2)由题意得:BA′=20米,BC′= =15(米),
则:CC′=15﹣7=8(米),
答:梯子的底端在水平方向滑动了8米.
解析:(1)根据勾股定理即可求出 梯子的顶端A距地面的高度.(2)根据勾股定理求出BE=15,由15-7=8(米)≠4(米)即可作出判断.
13. (1)解:( )2+1=n+1,Sn= (2)解:?∵OAn2=n ∴OA10= (3)解: 原式=()2+()2+()2+···+()2=(1+2+3+···+10)=.
解析:(1)根据数和式子的规律,写出符合条件的式子即可。 (2)在直角三角形中,根据勾股定理表示出长度即可。 (3)根据(1)中得出的规律进行计算求值。
一、单选题
1.下列三条线段能构成直角三角形的是( ??)
A.?6, 7, 8????????????????????????????????B.?2, 3, 4????????????????????????????????C.?3, 4, 6????????????????????????????????D.?6,8, 10
2.在直线l上有三个正方形m、q、n,若m、q的面积分别为5和11,则n的面积( ??)
A.?4??????????????????????????????????????????
B.?6??????????????????????????????????????????
C.?16??????????????????????????????????????????
D.?55
3.将一根长24cm的筷子置于底面直径为5cm,高为12cm的圆柱水杯中,设筷子露在杯子外面的长度为h,则h的取值范围是( ??) 21教育网
A.?12cm≤h≤19cm?????????????
B.?12cm≤h≤13cm?????????????
C.?11cm≤h≤12cm?????????????
D.?5cm≤h≤12cm
4.如图,在矩形ABCD中,AB=6,BC=8,点E是BC边上一点,将△ABE沿AE折叠,使点B落在点F处,连结CF,当△CEF为直角三角形时,BE的长是( ??) 21cnjy.com
A.?4????????????????????????????????????????
B.?3???????????????????????????????????????
C.?4或8????????????????????????????????????????
D.?3或6
5.如图,在边长为1个单位长度的小正方形组成的网格中,点A、B都是格点,则线段AB的长度为( ??)
A.?5???????????????????????????????????????????
B.?6???????????????????????????????????????????
C.?7???????????????????????????????????????????
D.?25
二、填空题
6.公元3世纪初,中国古代数学家赵爽注《周髀算经》时,创造了“赵爽弦图”.如图,设勾 ,弦 ,则小正方形ABCD的面积是________. 21·cn·jy·com
7.如图,在 中, ,若 边上的中线 垂直相交于 点,则 ________.
8.如图,点D、E分别是直角△ABC的边AB和BC的点,将△BDE沿DE翻折到△ADE,若∠C=90°,AC=2 ,BC=8,则DE的长为________; www.21-cn-jy.com
三、解答题
9.A,B两个居民楼在公路同侧,它们离公路的距离分别为AE=200米,BF=70米,它们的水平距离EF=390米.现欲在公路旁建一个超市P,使超市到两居民楼的距离相等,则超市应建何处?为什么?
10.如图,BC=3cm,AB=4cm,AF=12cm,且∠B=∠FAC=90°,求正方形CDEF的面积.
11.铁路上A,B两站(视为直线上的两点)相距50km,C,D为两村庄(视为两个点),DA⊥AB于点A,CB⊥AB于点B(如图).已知DA=20km,CB=10km,现在要在铁路AB上建一个土特产收购站E,使得C,D两村庄到收购站E的直线距离相等,请你设计出收购站的位置,并计算出收购站E到A站的距离. 2·1·c·n·j·y
四、综合题
12.一架云梯长25 m,如图所示斜靠在一面墙上,梯子底端C离墙7 m.
(1)这个梯子的顶端A距地面有多高?
(2)如果梯子的顶端下滑了4 m,那么梯子的底部在水平方向也是滑动了4 m吗?
13.细心观察图,认真分析各式,然后解答下列问题.
( )2+1=2,S1= ;
( )2+1=3,S2= ;
( )2+1=4,S3= ;
……
(1)请用含有n(n是正整数)的等式表示上述变化规律;
(2)推算出OA10的长;
(3)求 + + +…+ 的值.
答案解析部分
一、单选题
1. D
解析:A、最大边82=64<62+72=85, 为锐角三角形,A不符合题意; B、最大边42=16>32+22=13, 为钝角三角形,B不符合题意; C、最大边62=36>32+42=25, 为钝角三角形,C不符合题意; C、最大边102=100=62+82=100, 为直角三角形,D不符合题意; 故答案为:D 【分析】先找出最大边,然后根据勾股定理分析判断,最大边的平方小于另外两边的平方和是锐角三角形,等于另外两边的平方和是直角三角形,大于另外两边的平方和是钝角三角形。育·网】
2. C
解析: ∵∠ACB+∠ECD=∠ACB+∠BAC=90°, ∴∠ABC=∠DEC,∠ACB=∠CDE,AC=CD, ∴△ACB≌△△DCE(AAS), ∴AB=CE,BC=DE, 由勾股定理可得,AC2=AB2+BC2=AB2+DE2 Sn=Sm+Sq=11+5=16. n的面积为16 21·世纪*教育网
故答案为:C.
【分析】利用全等三角形判定定理证明,再利用勾股定理求得线段的关系,得到面积。
3. C
解析: h最大时为筷子与杯底垂直时,h=12cm 最小时为筷子与杯底和杯高形成直角三角形时,AB= h=24-13=11cm, ∴11cm≤h≤12cm. www-2-1-cnjy-com
故答案为:C.
【分析】根据题意,找到h最小、最大值的情况,利用勾股定理解答。
4. D
解析:(1)当∠EFC=90°时, ∵∠AFE=∠ABE=90°, ∴∠AFE+∠EFC=180°, ∴A、F、C在同一条直线上, ∴AF=AB=6, ∴FC=AC-AF=10-6=4, 设BE=x, 则EF=x,EC=BC-BE=8-x, 由勾股定理得:EF2+FC2=EC2 , 即x2+42=(8-x)2, ∴x=3,即EF=3; 2)当点F在AD上时, A、F、D在同一条直线上, 这时四边形ABED是矩形, ∵△AFE是由△ABE折叠而得, ∴AF=AB=6, ∴BE=AF=6. 故答案为:D.21世纪教育网版权所有
【分析】△CEF为直角三角形有两种情况,即F在AC上时,或F在AD上时,分别利用折叠图形的特点找出相关相等的线段,设未知数,利用勾股定理列式即可解决。21*cnjy*com
5. A
解析:根据图形,利用勾股定理可得: ,故答案为:A.
【分析】利用方格纸的特点可知:AB是两直角边分别为3与4的直角三角形的斜边,利用勾股定理即可求出AB的长。【来源:21cnj*y.co*m】
二、填空题
6. 4
解析:∵勾 ,弦 ,
∴股b= ,
∴小正方形的边长= ,
∴小正方形的面积
故答案为:4 【分析】根据勾股定理计算得到b的长度,即可得到小正方形的边长计算其面积即可。
7.
解析:∵AD、BE分别为BC,AC的中线, ∴BD=BC=4,AE=AC=3, ∵点O是△ABC的重心, ∴AO=2OD,BO=2OE, ∵BE⊥AD, ∴∠AOE=∠BOD=90°, ∴AO2+OE2=AE2=9,BO2+OD2=BD2=16, ∴AO2+BO2=9①,BO2+OA2=16②, ①+②得AO2+OB2=25, ∴AO2+OB2=20, ∵AO2+OB2=AB2 , ∴AB=. 故答案为:. 【分析】根据三角形的中线,可得BD=BC=4,AE=AC=3,AO=2OD,BO=2OE.利用勾股定理可得AO2+OE2=AE2=9,BO2+OD2=BD2=16,从而可得AO2+BO2=9①,BO2+OA2=16②,两等式相加可得AO2+OB2=20,从而可求出AB的长.【出处:21教育名师】
8.
解析:∵在直角三角形ABC中,AC=2 ,BC=8
∴ =
故BD=
∵△BDE沿DE翻折到△ADE
∴BE=AE
所以CE=BC-BE=8-BE
在直角三角形△ABE中
即
解得AE=
故CE=
在直角三角形BDE中
= 【分析】先根据勾股定理求出AB的长,根据点D是AB的中点求出BD的长,根据翻折的性质求出CE=BC-BE=8-BE,然后在直角三角形△ABE中根据勾股定理列出关于AE的方程求出AE,进而求出CE,再根据勾股定理求出DE即可.2-1-c-n-j-y
三、解答题
9.解:设 米,则 米,由题意得: 解得: .故:超市应建在距离E处150米的位置. 【版权所有:21教育】
解析:根据勾股定理由题意可知AP=BP,因此设EP=x表示出PF,然后根据AP2=BP2建立关于x的方程,求解即可。21教育名师原创作品
10.解:∵∠B=90°, ∴AB2+BC2=AC2 , ∵AB=4,BC=3, ∴AC=5 ∵∠FAC=90°, ∴AC2+AF2=CF2 , ∵AC=5,AF =12, ∴CF=13 ∵S正方形CDEF=CF2 ∴S正方形CDEF=169。
解析:由题意可知,ΔABC与ΔACF都是直角三角形,由勾股定理可以分别求出AC与CF的长,正方形CDEF的面积等于边长的平方,即CF的平方,即可求得正方形CDEF的面积。
11.解: 连接DE,CE,设AE=x km,则BE=(50-x) km , 在Rt△ADE中, , ∴ 在Rt△BCE中, ?, ∴CE2=102+(50-x)2 , 又DE=CE, ∴202+x2=102+(50-x)2 , 解得x=22 ∴收购站E到A站的距离为22km。
解析:根据题意,作线段CD的垂直平分线交AB于点E,连接DE、CE。设AE=x km,则BE=(50-x) km ,在Rt△ADE和Rt△BCE中,用勾股定理表示出DE和CE,再根据等量关系DE=CE列方程求解即可。
四、综合题
12. (1)由题意得:AC=25米,BC=7米,
AB= =24(米),
答:这个梯子的顶端距地面有24米; (2)由题意得:BA′=20米,BC′= =15(米),
则:CC′=15﹣7=8(米),
答:梯子的底端在水平方向滑动了8米.
解析:(1)根据勾股定理即可求出 梯子的顶端A距地面的高度.(2)根据勾股定理求出BE=15,由15-7=8(米)≠4(米)即可作出判断.
13. (1)解:( )2+1=n+1,Sn= (2)解:?∵OAn2=n ∴OA10= (3)解: 原式=()2+()2+()2+···+()2=(1+2+3+···+10)=.
解析:(1)根据数和式子的规律,写出符合条件的式子即可。 (2)在直角三角形中,根据勾股定理表示出长度即可。 (3)根据(1)中得出的规律进行计算求值。
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
