北师大版数学九下2.2二次函数的图像和性质课件(共3课时、67张ppt)
文档属性
| 名称 | 北师大版数学九下2.2二次函数的图像和性质课件(共3课时、67张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 4.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-02-22 18:08:56 | ||
图片预览



文档简介
(共67张PPT)
2.2二次函数的图象与性质
(第1课时)
1.二次函数的定义
一般地,形如y=ax2+bx+c(a,b,c是常数,a≠0)的函数叫做x的二次函数.
(1)列表.
(3)连线.
(2)描点.
2.画函数图象的主要步骤是什么?
数形结合,直观感受
在二次函数y=x2中,y随x的变化而变化的规律是什么?
观察y=x2的表达式,选择适当x值,并计算相应的y值,完成下表:
你会用描点法画二次函数y=x2的图象吗?
<列表>
x
y=x2
x … -3 -2 -1 0 1 2 3 …
y=x2
x
y=x2 … 9 4 1 0 1 4 9 …
x
y
O
-4
-3
-2
-1
1
2
3
4
10
8
6
4
2
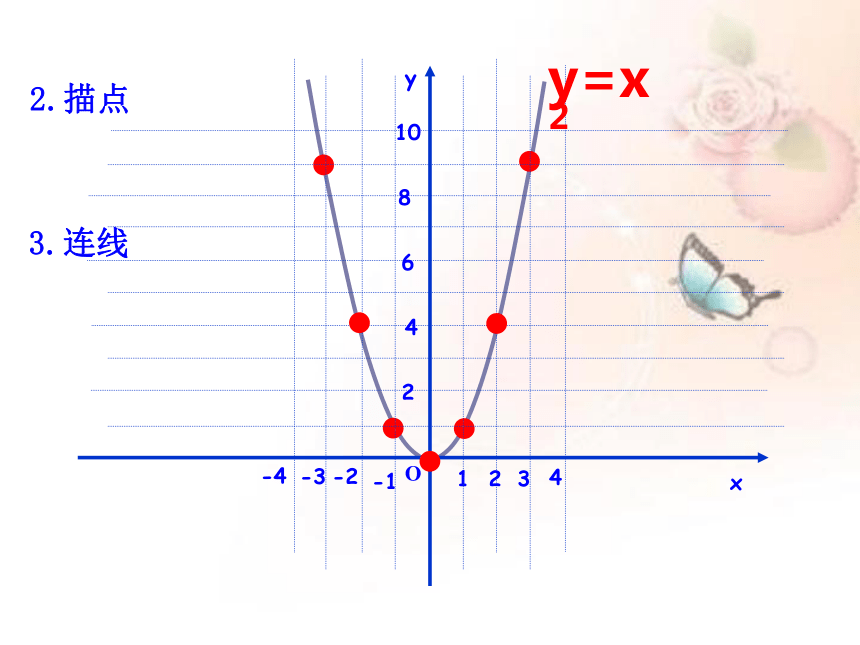
y=x2
2.描点
3.连线
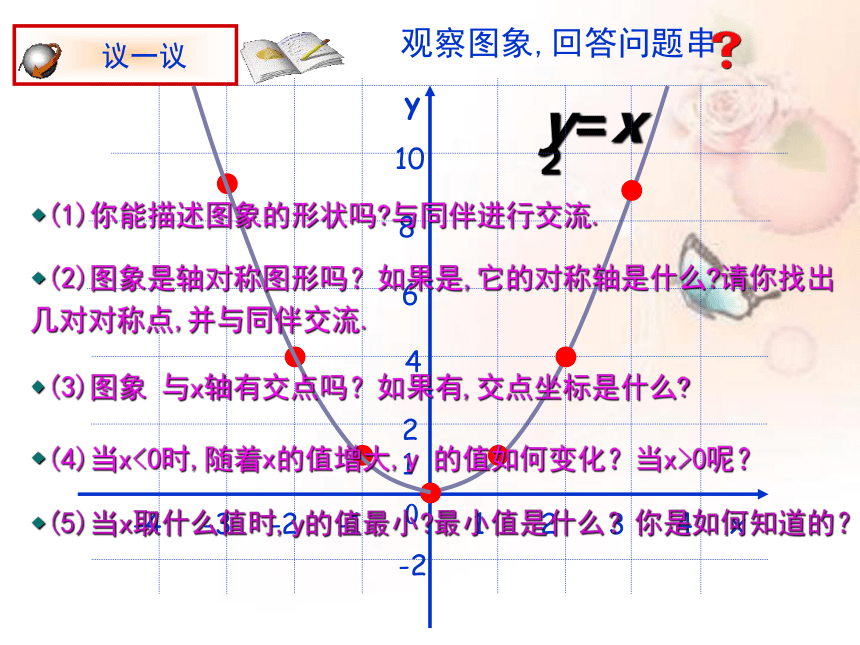
观察图象,回答问题串
(1)你能描述图象的形状吗?与同伴进行交流.
(2)图象是轴对称图形吗?如果是,它的对称轴是什么?请你找出几对对称点,并与同伴交流.
(3)图象 与x轴有交点吗?如果有,交点坐标是什么?
(4)当x<0时,随着x的值增大,y 的值如何变化?当x>0呢?
(5)当x取什么值时,y的值最小?最小值是什么?你是如何知道的?
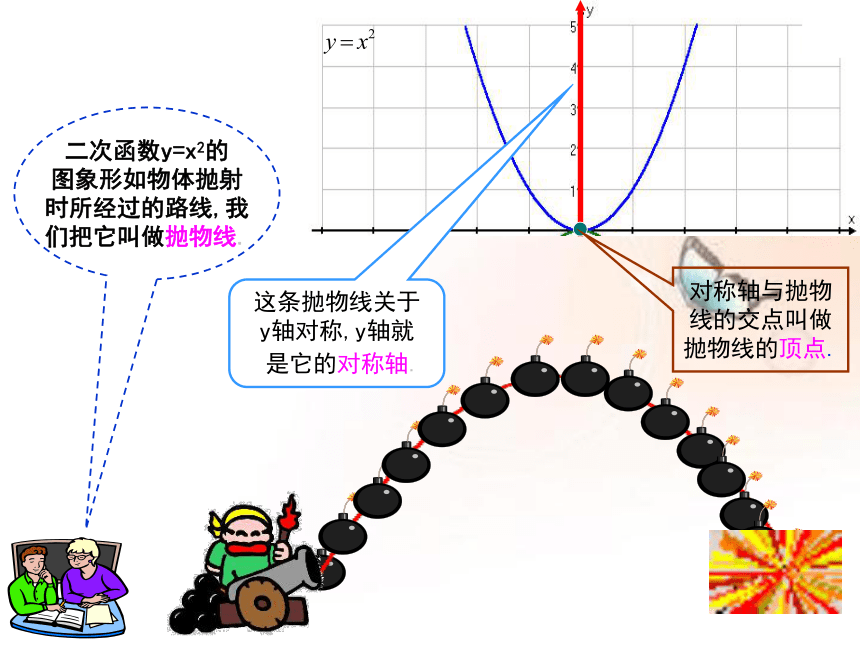
这条抛物线关于
y轴对称,y轴就
是它的对称轴.
对称轴与抛物
线的交点叫做
抛物线的顶点.
二次函数y=x2的
图象形如物体抛射
时所经过的路线,我
们把它叫做抛物线.
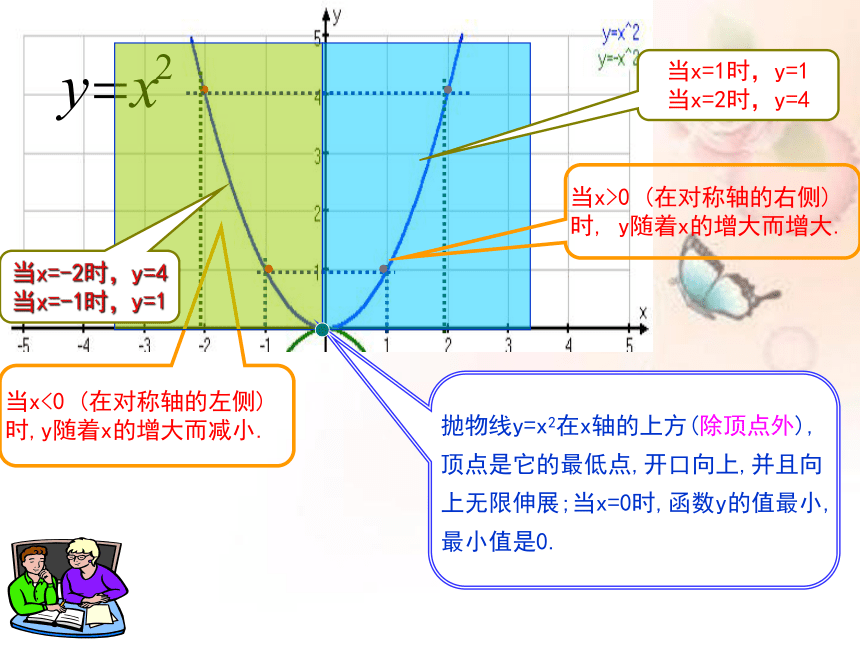
当x<0 (在对称轴的左侧)时,y随着x的增大而减小.
当x>0 (在对称轴的右侧)时, y随着x的增大而增大.
当x=-2时,y=4
当x=-1时,y=1
当x=1时,y=1
当x=2时,y=4
抛物线y=x2在x轴的上方(除顶点外),顶点是它的最低点,开口向上,并且向上无限伸展;当x=0时,函数y的值最小,最小值是0.
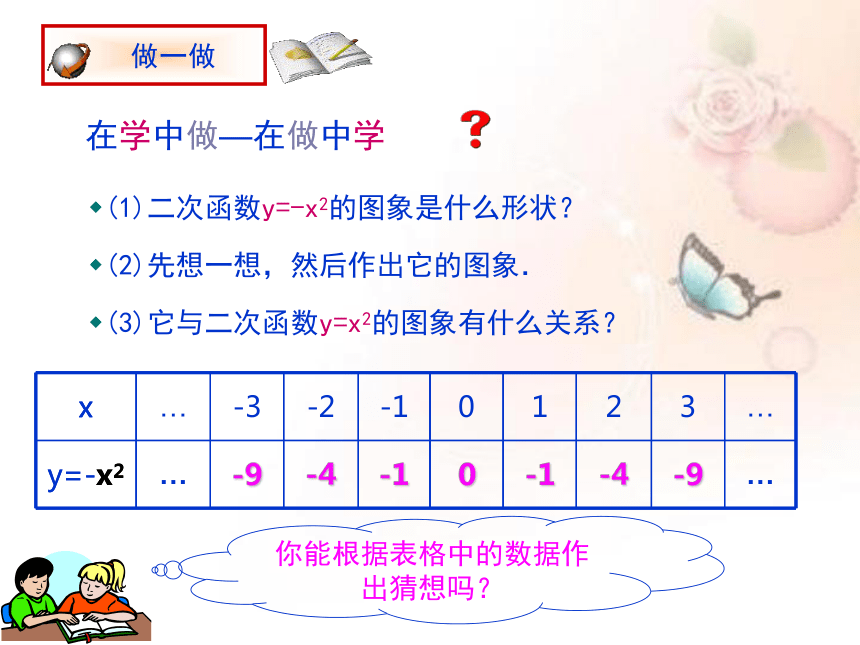
在学中做—在做中学
(1)二次函数y=-x2的图象是什么形状?
你能根据表格中的数据作出猜想吗?
(2)先想一想,然后作出它的图象.
(3)它与二次函数y=x2的图象有什么关系?
x
y=-x2
x … -3 -2 -1 0 1 2 3 …
y=-x2
x
… -9 -4 -1 0 -1 -4 -9 …
x
y
0
-4
-3
-2
-1
1
2
3
4
-10
-8
-6
-4
-2
2
-1
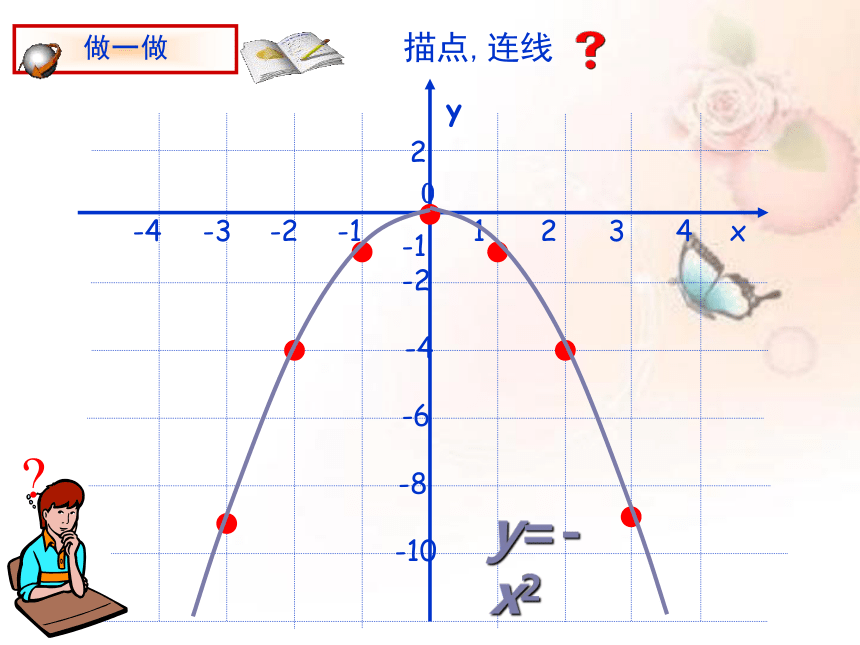
描点,连线
y=-x2
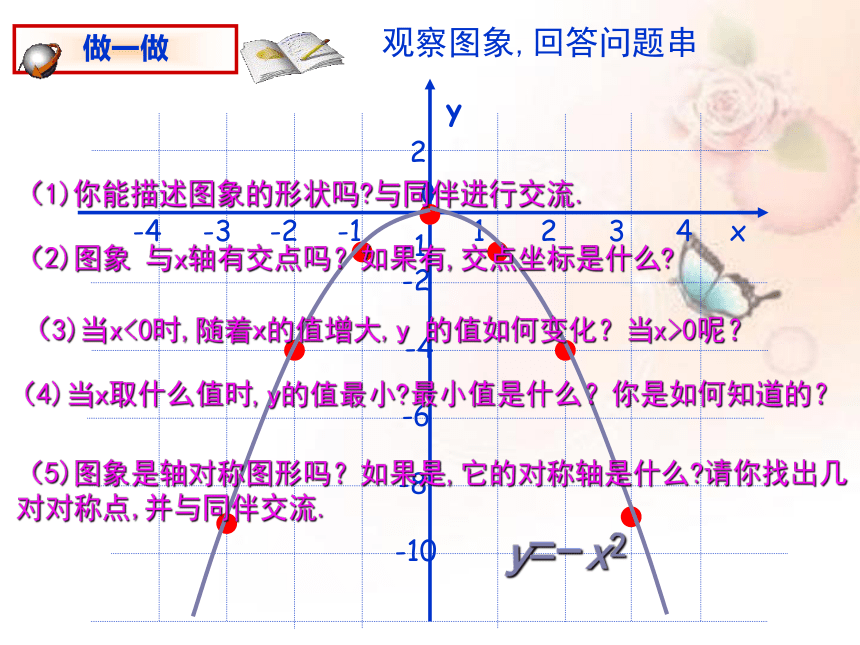
观察图象,回答问题串
(1)你能描述图象的形状吗?与同伴进行交流.
(2)图象 与x轴有交点吗?如果有,交点坐标是什么?
(3)当x<0时,随着x的值增大,y 的值如何变化?当x>0呢?
(4)当x取什么值时,y的值最小?最小值是什么?你是如何知道的?
(5)图象是轴对称图形吗?如果是,它的对称轴是什么?请你找出几对对称点,并与同伴交流.
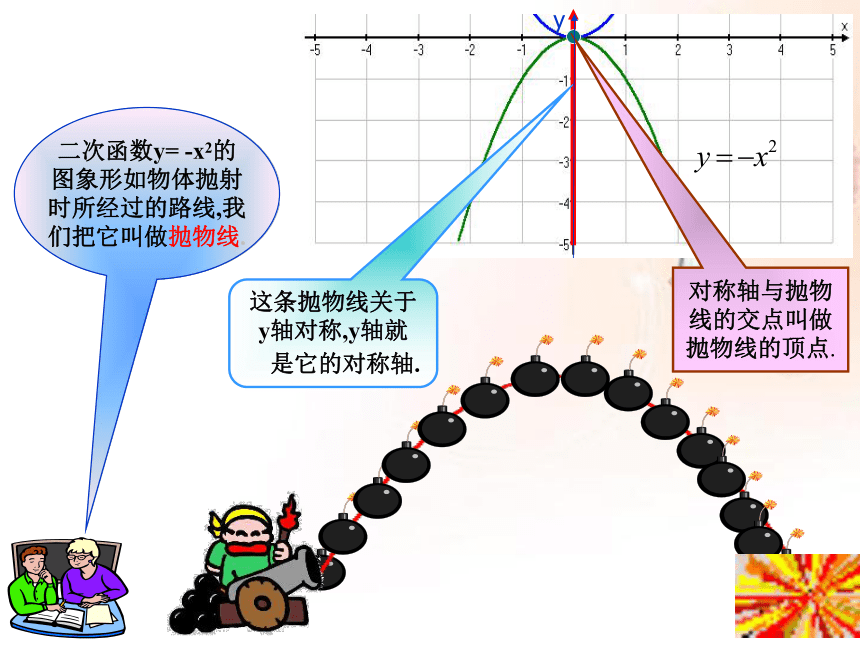
y=-x2
这条抛物线关于
y轴对称,y轴就
是它的对称轴.
对称轴与抛物
线的交点叫做
抛物线的顶点.
二次函数y= -x2的
图象形如物体抛射
时所经过的路线,我
们把它叫做抛物线.
y
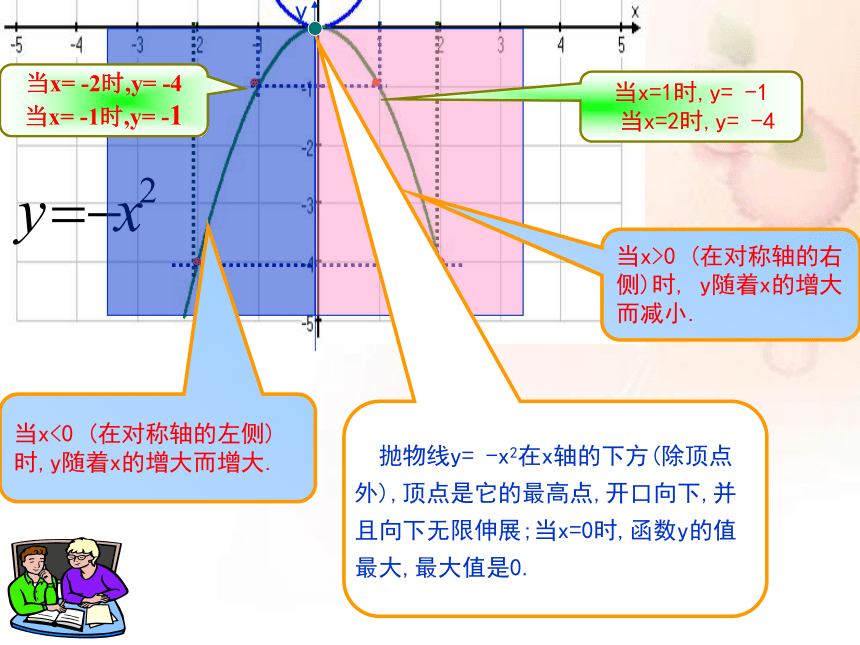
当x<0 (在对称轴的左侧)时,y随着x的增大而增大.
当x>0 (在对称轴的右侧)时, y随着x的增大而减小.
y
当x= -2时,y= -4
当x= -1时,y= -1
当x=1时,y= -1
当x=2时,y= -4
抛物线y= -x2在x轴的下方(除顶点外),顶点是它的最高点,开口向下,并且向下无限伸展;当x=0时,函数y的值最大,最大值是0.
函数y=ax2(a≠0)的图象和性质
y=x2
y=-x2
它们之间有何关系?
二次函数y=ax2的性质
1.顶点坐标与对称轴
2.位置与开口方向
3.增减性与最值
抛物线
顶点坐标
对称轴
位置
开口方向
增减性
最值
y=x2
y= -x2
(0,0)
(0,0)
y轴
y轴
在x轴的上方(除顶点外)
在x轴的下方( 除顶点外)
向上
向下
当x=0时,最小值为0.
当x=0时,最大值为0.
在对称轴的左侧,y随着x的增大而减小. 在对称轴的右侧, y随着x的增大而增大.
在对称轴的左侧,y随着x的增大而增大. 在对称轴的右侧, y随着x的增大而减小.
根据图形填表:
y=x2和y=-x2是y=ax2当a=±1时的特殊例子.a的符号确定着抛物线的……
函数y=ax2(a≠0)的图象和性质:
在同一坐标系中作出函数y=x2和y=-x2的图象
y=x2
y=-x2
1.抛物线y=ax2的顶点是原点,对称轴是y轴.
2.当a>0时,抛物线y=ax2在x轴的上方(除顶点外),它的开口向上,并且向上无限伸展; 当a<0时,抛物线y=ax2在x轴的下方(除顶点外),它的开口向下,并且向下无限伸展.
3.当a>0时,在对称轴的左侧,y随着x的增大而减小;在对称轴右侧,y随着x的增大而增大.当x=0时函数y的值最小.当a<0时,在对称轴的左侧,y随着x的增大而增大;在对称轴的右侧,y随着x增大而减小,当x=0时,函数y的值最大.
二次函数y=ax2的性质
我思,我进步
1.已知抛物线y=ax2经过点A(-2,-8).
(1)求此抛物线的函数解析式;
(2)判断点B(-1,- 4)是否在此抛物线上.
(3)求出此抛物线上纵坐标为-6的点的坐标.
解:(1)把(-2,-8)代入y=ax2,得 -8=a(-2)2,
解得a= -2,所求函数解析式为y= -2x2.
1.抛物线y=2x2的顶点坐标是 ,对称轴是 .在 侧,y随着x的增大而增
大;在 侧,y随着x的增大而减小,当x= 时,函数y的值最小,最小值是 ,抛物线y=2x2在x轴的 方(除顶点外).
2.抛物线 在x轴的 方(除顶点外),在对称轴的左侧,y随着x的 ;在对称轴的右侧,y随着x的 ,当x=0时,函数y的值最大,最大值是 ,当x 时,y<0.
(0,0)
y轴
对称轴的右
对称轴的左
0
0
上
下
增大而增大
增大而减小
0
【跟踪训练】
回味无穷
2.当a>0时,抛物线y=ax2在x轴的上方(除顶点外),它的开口 向上,并且向上无限伸展;当a<0时,抛物线y=ax2在x轴的下方(除顶点外),它的开口向下,并且向下无限伸展.
3.当a>0时,在对称轴的左侧,y随着x的增大而减小;在对称轴 右侧,y随着x的增大而增大.当x=0时函数y的值最小.
当a<0时,在对称轴的左侧,y随着x的增大而增大;在对称轴的右侧,y随着x增大而减小,当x=0时,函数y的值最大
1.抛物线y=ax2的顶点是原点,对称轴是y轴.
由二次函数y=x2和y=-x2知:
2.2二次函数的图象与性质
(第2课时)
你能用配方的方法把y=3x2-6x+5变形成y=3(x-1)2+2的形式吗?
二次函数y=ax?+bx+c的图象
二次函数y=3x2-6x+5的图象是什么形状?它与我们已经作过的二次函数的图象有什么关系?
在同一坐标系中作出二次函数y=3x2和y=3(x-1)2的图象.
由于y=3x2-6x+5=3(x-1)2+2,因此我们先作二次函数y=3(x-1)2的图象.
比较函数 与 的图象
(2)在同一坐标系中作出二次函数y=3x2和y=3(x-1)2的图象.
⑴完成下表,并比较3x2和3(x-1)2的值,它们之间有什么关系?
x -3 -2 -1 0 1 2 3 4
27 12 3 0 3 12 27 48
27 12 3 0 3 12 27 48
48 27 12 3 0 3 12 27
观察图象,回答问题
(3)函数y=3(x-1)2的图象与y=3x2的图象有什么关系?它是轴对称图形吗?它的对称轴和顶点坐标分别是什么?
(4)x取哪些值时,函数y=3(x-1)2的值随x值的增大而增大?x取哪些值时,函数y=3(x-1)2的值随x的增大而减少?
图象是轴对称图形
对称轴是平行于
y轴的直线:x=1.
顶点坐标
是点(1,0).
二次函数y=3(x-1)2
与y=3x2的图象形状
相同,可以看作是抛
物线y=3x2整体沿x轴
向右平移了1 个单位
(3)函数y=3(x-1)2的图象与y=3x2的图象有什么关系?它是轴对称图形吗?它的对称轴和顶点坐标分别是什么?
二次项系数相同
a>0,开口都向上.
想一想,在同一坐标系中作二次函数y=3(x+1)2的图象,会在什么位置?
在对称轴(直线:x=1)左侧
(即x<1时),函数y=3(x-1)2
的值随x的增大而减少,.
顶点是最低点,函数
有最小值.当x=1时,
最小值是0..
二次函数y=3(x-1)2
与y=3x2的增减性类似.
(4)x取哪些值时,函数y=3(x-1)2的值随x值的增大而增大?x取哪些值时,函数y=3(x-1)2的值随x的增大而减少?
在对称轴(直线:x=1)左侧
(即x>1时),函数y=3(x-1)2
的值随x的增大而增大,.
想一想,在同一坐标系中作出二次函数y=3(x+1)2的图象,它的增减性会是什么样?
真知 从实践走来
1.在上面的坐标系中作出二次函数y=3(x+1)2的图象.它与二次函数y=3x2和y=3(x-1)2的图象有什么关系?它是轴对称图形吗?它的对称轴和顶点坐标分别是什么?
2.x取哪些值时,函数y=3(x+1)2的值随x值的增大而增大?x取哪些值时,函数y=3(x+1)2的值随x的增大而减少?
在同一坐标系中作出二次函数y=3x2,y=3(x-1)2和y=3(x+1)2的图象.
完成下表,并比较3x2,3(x-1)2和3(x+1)2的值,它们之间有什么关系?
函数y=a(x-h)2(a≠0)的图象和性质
x -4 -3 -2 -1 0 1 2 3 4
27 12 3 0 3 12 27
27 12 3 0 3 12 27
27 12 3 0 3 12 27
27 12 3 0 3 12 27
图象是轴对称图形.
对称轴是平行于
y轴的直线:x= -1.
顶点坐标
是点(-1,0).
二次函数y=3(x+1)2
与y=3x2的图象形状
相同,可以看作是抛
物线y=3x2整体沿x轴
向左平移了1 个单位.
1.函数y=3(x+1)2的图象与y=3x2和y=3(x-1)2的图象有什么关系?它是轴对称图形吗?它的对称轴和顶点坐标分别是什么?
二次项系数相同
a>0,开口都向上.
想一想,二次函数y=3(x+1)2的图象的增减性会怎样?
在对称轴(直线:x=-1)左侧
(即x<-1时),函数y=3(x+1)2
的值随x的增大而减少,.
顶点是最低点,函数
有最小值.当x=-1时,
最小值是0..
二次函数y=3(x+1)2
与y=3x2的增减性类似.
2.x取哪些值时,函数y=3(x+1)2的值随x值的增大而增大?x取哪些值时,函数y=3(x+1)2的值随x的增大而减少?
在对称轴(直线:x=-1)右侧
(即x>-1时),函数y=3(x+1)2
的值随x的增大而增大,.
猜一猜,函数y=-3(x-1)2,y=-3(x+1)2和y=-3x2的图象的位置和形状.
请你总结二次函数y=a(x-h)2的图象和性质.
www.1230.org 初中数学资源网
2.抛物线y=-3(x-1)2和y=-3(x+1)2在x轴的下方(除顶点外),它的开口向下,并且向下无限伸展.
3.抛物线y=-3(x-1)2在对称轴(x=1)的左侧,当x<1时, y随着x的增大而增大;在对称轴(x=1)右侧,当x>1时, y随着x的增大而减小.当x=1时,函数y的值最大(是0);
抛物线y=-3(x+1)2在对称轴(x=-1)的左侧,当x<-1时, y随着x的增大而增大;在对称轴(x=-1)右侧,当x>-1时, y随着x的增大而减小.当x=-1时,函数y的值最大(是0).
二次函数y=-3(x-1)2,y=-3(x+1)2和y=-3x2的图象
4.抛物线y=-3(x-1)2可以看作是抛物线y=-3x2沿x轴向右平移了1个单位;抛物线y=-3(x+1)2可以看作是抛物线y=-3x2沿x轴向左平移了1个单位.
X=-1
X=1
1.抛物线y=-3(x-1)2的顶点是(1,0);对称轴是直线:x=1;抛物线y=-3(x+1)2的顶点是(-1,0);对称轴是直线:x=-1.
www.1230.org 初中数学资源网
1.抛物线y=a(x-h)2的顶点是(h,0),对称轴是平行于y轴的直线x=h.
3.当a>0时,在对称轴(x=h)的左侧,y随着x的增大而减小;在对称轴(x=h)右侧,y随着x的增大而增大;当x=h时函数y的值最小(是0).
当a<0时,在对称轴(x=h)的左侧,y随着x的增大而增大;在对称轴(x=h)的右侧,y随着x增大而减小;当x=h时,函数y的值最大(是0).
二次函数y=a(x-h)2的性质
2.当a>0时,抛物线y=a(x-h)2在x轴的上方(除顶点外),它的开口向上,并且向上无限伸展;
当a<0时,抛物线y=a(x-h)2在x轴的下方(除顶点外),它的开口向下,并且向下无限伸展.
X=h
X=h
二次函数y=a(x-h)2的性质
1.顶点坐标与对称轴
2.位置与开口方向
3.增减性与最值
抛物线
顶点坐标
对称轴
位置
开口方向
增减性
最值
y=a(x-h)2 (a>0)
y=a(x-h)2 (a<0)
(h,0)
(h,0)
直线x=h
直线x=h
在x轴的上方(除顶点外)
在x轴的下方( 除顶点外)
向上
向下
当x=h时,最小值为0.
当x=h时,最大值为0.
在对称轴的左侧,y随着x的增大而减小. 在对称轴的右侧, y随着x的增大而增大.
在对称轴的左侧,y随着x的增大而增大. 在对称轴的右侧, y随着x的增大而减小.
根据图形填表:
开口大小
我思,我进步
在同一坐标系中作出二次函数y=3x?,y=3(x-1)2和y=3(x-1)2+2的图象.
二次函数y=3x?,y=3(x-1)2和y=3(x-1)2+2的图象有什么关系?它们的开口方向,对称轴和顶点坐标分别是什么?作图看一看.
在同一坐标系中作出函数y=3x?,y=3(x-1)2和y=3(x-1)2+2的图象.
完成下表,并比较3x2,3(x-1)2和3(x-1)2+2值,它们之间有何关系?
函数y=a(x-h)2+k(a≠0)的图象和性质
x -4 -3 -2 -1 0 1 2 3 4
27 12 3 0 3 12 27
27 12 3 0 3 12 27
27 12 3 0 3 12 27
29 14 5 2 5 14 29
对称轴仍是平行于y轴的直
线(x=1);增减性与y=3x2类似.
顶点是(1,2).
二次函数y=3(x-1)2+2的
图象可以看作是抛物线
y=3x2先沿着x轴向右平移
1个单位,再沿直线x=1向
上平移2个单位后得到的.
二次函数y=3(x-1)2+2的图象和抛物线y=3x?,y=3(x-1)2有什么关系?它的开口方向,对称轴和顶点坐标分别是什么?
开口向上,当
X=1时有最小
值:且最小值=2.
先猜一猜,再做一做,在同一坐标系中作二次函数y=3(x-1)2-2,会是什么样?
X=1
对称轴仍是平行于y轴的直线
(x=1);增减性与y=3x2类似.
顶点是(1,-2).
二次函数y=3(x-1)2-2的
图象可以看作是抛物线
y=3x2先沿着x轴向右平移
1个单位,再沿直线x=1向
下平移2个单位后得到的.
二次函数y=3(x-1)2-2的图象与抛物线y=3x2和y=3(x-1)2有何关系?它的开口方向、对称轴和顶点坐标分别是什么?
开口向上,
当x=1时y有
最小值:且
最小值= -2.
想一想,二次函数y=-3(x-1)2+2和y=-3x?,y=-3(x-1)2的图象有什么关系?它们的开口方向,对称轴和顶点坐标分别是什么?再作图看一看.
X=1
我思,我进步
在同一坐标系中作出二次函数y=-3(x-1)2+2,y=-3(x-1)2-2,y=-3x?和y=-3(x-1)2的图象
二次函数y=-3(x-1)2+2与y=-3(x-1)2-2和y=-3x?,y=-3(x-1)2的图象有什么关系?它们是轴对称图形吗?它的开口方向、对称轴和顶点坐标分别是什么?当x取哪些值时,y的值随x值的增大而增大?当x取哪些值时,y的值随x值的增大而减小?
对称轴仍是平行于y轴的直线
(x=1);增减性与y= -3x2类似.
顶点分别是
(1,2)和(1,-2).
二次函数y=-3(x-1)2+2与
y=-3(x-1)2+2的图象可
以看作是抛物线y=-3x2
先沿着x轴向右平移1个
单位,再沿直线x=1向上
(或向下)平移2个单位后
得到的.
二次函数y=-3(x-1)2+2与y=-3(x-1)2-2的图象和抛物线y=-3x?,y=-3(x-1)2有什么关系? 它的开口方向,对称轴和顶点坐标分别是什么?
想一想,二次函数y=-3(x+1)2+2与y=-3(x+1)2-2的图象和抛物线y=-3x?,y=-3(x+1)2
y
X=1
对称轴仍是平行于y轴的直线
(x=-1);增减性与y= -3x2类似.
顶点分别是
(-1,2)和(-1,-2)..
二次函数y=-3(x+1)2+2与
y=-3(x+1)2-2的图象可
以看作是抛物线y=-3x2
先沿着x轴向左平移1个
单位,再沿直线x=-1向上
(或向下)平移2个单位后
得到的.
二次函数y=-3(x-1)2+2与y=-3(x-1)2-2的图象和抛物线y=-3x?,y=-3(x-1)2有什么关系? 它的开口方向,对称轴和顶点坐标分别是什么?
开口向下,
当x=-1时y有
最大值:且
最大值= 2
(或最大值=-2).
先想一想,再总结二次函数y=a(x-h)2+k的图象和性质.
X=1
一般地,由y=ax?的图象便可得到二次函数y=a(x-h)?+k的图象:y=a(x-h)?+k(a≠0) 的图象可以看成y=ax?的图象先沿x轴整体左(右)平移|h|个单位(当h>0时,向右平移;当h<0时,向左平移),再沿对称轴整体上(下)平移|k|个单位 (当k>0时向上平移;当k<0时,向下平移)得到的.
因此,二次函数y=a(x-h)?+k的图象是一条抛物线,它的开口方向、对称轴和顶点坐标与a,h,k的值有关.
二次函数y=a(x-h)?+k与=ax?的关系
在对称轴的左侧,y随着x的增大而增大. 在对称轴的右侧, y随着x的增大而减小.
二次函数y=a(x+h)2+k的图象和性质
1.顶点坐标与对称轴
2.位置与开口方向
3.增减性与最值
抛物线
顶点坐标
对称轴
位置
开口方向
增减性
最值
y=a(x-h)2+k(a>0)
y=a(x-h)2+k(a<0)
(-h,k)
(-h,k)
直线x=h
直线x=h
由h和k的符号确定
由h和k的符号确定
向上
向下
当x=h时,最小值为k.
当x=h时,最大值为k.
在对称轴的左侧,y随着x的增大而减小. 在对称轴的右侧, y随着x的增大而增大.
根据图形填表:
1.相同点: (1)形状相同(图像都是抛物线,开口方向相同).
(2)都是轴对称图形.
(3)都有最(大或小)值.
(4)a>0时, 开口向上,在对称轴左侧,y都随x的增大而减小,在对称轴右侧,y都随 x的增大而增大. a<0时,开口向下,在对称轴左侧,y都随x的增大而增大,在对称轴右侧,y都随 x的增大而减小 .
2.不同点: 只是位置不同(1)顶点不同:分别是(-h,k)和(0,0).
(2)对称轴不同:分别是直线x= -h和y轴.
(2)最值不同:分别是k和0.
3.联系: y=a(x-h)?+k(a≠0) 的图象可以看成y=ax?的图象先沿x轴整体左(右)平移|h|个单位(当h>0时,向右平移;当h<0时,向左平移),再沿对称轴整体上(下)平移|k|个单位 (当k>0时向上平移;当k<0时,向下平移)得到的.
回味无穷
二次函数y=a(x-h)?+k与=ax?的关系
1.下列二次函数中,图象以直线x=2为对称轴、且经过点(0,1)的是( ).
A.y=(x-2)2+1 B.y=(x+2)2+1
C.y=(x-2)2-3 D.y=(x+2)2-3
【解析】选C.根据以直线x=2为对称轴可知选项A,C符合,再根据图象经过点(0,1)知选项C符合.
2.将抛物线
向左平移1个单位后所得到的新抛物线的表达式为
_______________.
【答案】
3.将抛物线 先向上平移2个单位,再向右平移1个单位后,得到的抛物线的表达式为____________.
【答案】
【答案】选B.
4.把抛物线 向左平
移1个单位,然后向上平移3个单位,则平移后抛物线的表达式为( )
B.
C.
D.
A.
2.2二次函数的图象与性质
(第3课时)
1.指出下列二次函数的开口方向、对称轴和顶点坐标.
(1) y=2(x-3)2 -5
(2)y=-0.5(x+1)2
(3) y = 3(x+4)2+2
2.它们分别可以看成是由哪个函数图象通过怎样的平移得到的?
复习引入:
我们知道,作出二次函数y=3x2的图象,通过平移抛物线y=3x2可以得到二次函数y=3x2-6x+5的图象.
那是怎样平移的呢?
y=3x2-6x+5
=3(x-1)2+2
只要将表达式右边进行配方就可以知道了.
配方后的表达式通常称为配方式或顶点式
这个结果通常称为顶点坐标公式.
二次函数y=ax?+bx+c的顶点式
【探究新知】
因此,二次函数y=ax?+bx+c的图象是一条抛物线.
结论 顶点坐标公式
根据公式确定下列二次函数图象的对称轴和顶点坐标:
【跟踪训练】
如图,桥梁的两条钢缆具有相同的抛物线形状.按照图中的直角坐标系,左面的一条抛物线可以用y= x?+ x+10
表示,而且左、右两条抛物线关于y轴对称.
⑴钢缆的最低点到桥面的距离是多少?
⑵两条钢缆最低点之间的距离是多少?
你有哪些计算方法?与同伴进行交流.
【例题】
⑴.钢缆的最低点到桥面的距离是少?你是怎样计算的?与同伴交流.
可以将函数y=0.0225x2+0.9x+10配方,求得顶点坐标,从而获得钢缆的最低点到桥面的距离;
⑵两条钢缆最低点之间的距离是多少?你是怎样计算的?与同伴交流.
想一想,你知道图中右面钢缆的表达式是什么吗?
⑶你还有其他方法吗?与同伴交流.
直接利用顶点坐标公式再计算一下上面问题中钢缆的最低点到桥面的距离以及两条钢缆最低点之间的距离.
1. 如图为抛物线y=ax2+bx+c的图象,A , B, C 为抛物线与坐标轴的交点,且OA=OC=1,则下列关系中正确的是( )
A.a+b=-1 B.a-b=-1
C.b<2a D.ac<0
选B.∵抛物线开口向上,∴a>0, ∵抛物线与y轴交于正半轴,∴c>0,∴ac>0,故D错;∵OA=OC=1,∴A,C两点的坐标分别为(-1,0),(0,1),∴当x=0时,y=1,即c=1;当x=-1时,y=0,即a-b+c=0,∴a-b=-c=-1,故B对;由图象可知x=1时,y>0,即a+b+c>0,∴a+b>-1,故A错;
∵对称轴 ,∴b>2a,故C错.
巩固练习
2.二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列结论①a,b异号;②当x=1和x=3时,函数值相等;③4a+b=0;④当y=4时,x的取值只能为0.其中正确的个数为( )
A.1 B.2
C.3 D.4
选C.
A.0,5 B.0,1
C.-4,5 D.-4,1
,
的值分别为( )
3. 若二次函数
配方后为
则
选D.
4.已知二次函数y=ax2+bx+c的图象如图所示,则下列结论正确的是( )
A.a>0 B.c<0
C.b2-4ac<0 D.a+b+c>0
选D.
x
y
O
选D.
6.已知二次函数
(a为常数),当a取不同的值时,其图象构成一个“抛物线系”.下图分别是当a=-1, a=0, a=1, a=2时二次函数的图象.它们的顶点在同一条直线上,这条直线的解析式是 .
【规律方法】
二次函数y=ax2+bx+c(a≠0)与y=ax?(a≠0)的关系
1.相同点: (1)形状相同(图象都是抛物线,开口方向相同).
(2)都是轴对称图形.
(3)都有最大(或小)值.
(4)a>0时, 开口向上,在对称轴左侧,y随x的增大而减小;在对称轴右侧,y随 x的增大而增大.a<0时,开口向下,在对称轴左侧,y随x的增大而增大;在对称轴右侧,y随 x的增大而减小 .
2.不同点: (1)位置不同.
(2)顶点不同:分别是 和(0,0).
(3)对称轴不同:分别是 和y轴.
(4)最值不同:分别是 和 0.
3.联系: (a≠0) 的图象可以看成y=ax?的
图象先沿x轴整体左(右)平移| |个单位(当
时向右平移,当 时向左平移),再沿对称轴
整体上(下)平移| |个单位 (当 >0时
向上平移;当 <0时,向下平移)得到的.
二次函数y=ax2+bx+c(a≠0)的图象和性质
1.顶点坐标与对称轴
2.位置与开口方向
3.增减性与最值
抛物线
顶点坐标
对称轴
位置
开口方向
增减性
最值
y=ax2+bx+c(a>0)
y=ax2+bx+c(a<0)
由a,b和c的符号确定
由a,b和c的符号确定
向上
向下
在对称轴的左侧,y随x的增大而减小. 在对称轴的右侧, y随x的增大而增大.
在对称轴的左侧,y随x的增大而增大. 在对称轴的右侧, y随x的增大而减小.
根据图形填表:
结束寄语
只有不断的思考,才会有新的发现;只有量的变化,才会有质的进步.
2.2二次函数的图象与性质
(第1课时)
1.二次函数的定义
一般地,形如y=ax2+bx+c(a,b,c是常数,a≠0)的函数叫做x的二次函数.
(1)列表.
(3)连线.
(2)描点.
2.画函数图象的主要步骤是什么?
数形结合,直观感受
在二次函数y=x2中,y随x的变化而变化的规律是什么?
观察y=x2的表达式,选择适当x值,并计算相应的y值,完成下表:
你会用描点法画二次函数y=x2的图象吗?
<列表>
x
y=x2
x … -3 -2 -1 0 1 2 3 …
y=x2
x
y=x2 … 9 4 1 0 1 4 9 …
x
y
O
-4
-3
-2
-1
1
2
3
4
10
8
6
4
2
y=x2
2.描点
3.连线
观察图象,回答问题串
(1)你能描述图象的形状吗?与同伴进行交流.
(2)图象是轴对称图形吗?如果是,它的对称轴是什么?请你找出几对对称点,并与同伴交流.
(3)图象 与x轴有交点吗?如果有,交点坐标是什么?
(4)当x<0时,随着x的值增大,y 的值如何变化?当x>0呢?
(5)当x取什么值时,y的值最小?最小值是什么?你是如何知道的?
这条抛物线关于
y轴对称,y轴就
是它的对称轴.
对称轴与抛物
线的交点叫做
抛物线的顶点.
二次函数y=x2的
图象形如物体抛射
时所经过的路线,我
们把它叫做抛物线.
当x<0 (在对称轴的左侧)时,y随着x的增大而减小.
当x>0 (在对称轴的右侧)时, y随着x的增大而增大.
当x=-2时,y=4
当x=-1时,y=1
当x=1时,y=1
当x=2时,y=4
抛物线y=x2在x轴的上方(除顶点外),顶点是它的最低点,开口向上,并且向上无限伸展;当x=0时,函数y的值最小,最小值是0.
在学中做—在做中学
(1)二次函数y=-x2的图象是什么形状?
你能根据表格中的数据作出猜想吗?
(2)先想一想,然后作出它的图象.
(3)它与二次函数y=x2的图象有什么关系?
x
y=-x2
x … -3 -2 -1 0 1 2 3 …
y=-x2
x
… -9 -4 -1 0 -1 -4 -9 …
x
y
0
-4
-3
-2
-1
1
2
3
4
-10
-8
-6
-4
-2
2
-1
描点,连线
y=-x2
观察图象,回答问题串
(1)你能描述图象的形状吗?与同伴进行交流.
(2)图象 与x轴有交点吗?如果有,交点坐标是什么?
(3)当x<0时,随着x的值增大,y 的值如何变化?当x>0呢?
(4)当x取什么值时,y的值最小?最小值是什么?你是如何知道的?
(5)图象是轴对称图形吗?如果是,它的对称轴是什么?请你找出几对对称点,并与同伴交流.
y=-x2
这条抛物线关于
y轴对称,y轴就
是它的对称轴.
对称轴与抛物
线的交点叫做
抛物线的顶点.
二次函数y= -x2的
图象形如物体抛射
时所经过的路线,我
们把它叫做抛物线.
y
当x<0 (在对称轴的左侧)时,y随着x的增大而增大.
当x>0 (在对称轴的右侧)时, y随着x的增大而减小.
y
当x= -2时,y= -4
当x= -1时,y= -1
当x=1时,y= -1
当x=2时,y= -4
抛物线y= -x2在x轴的下方(除顶点外),顶点是它的最高点,开口向下,并且向下无限伸展;当x=0时,函数y的值最大,最大值是0.
函数y=ax2(a≠0)的图象和性质
y=x2
y=-x2
它们之间有何关系?
二次函数y=ax2的性质
1.顶点坐标与对称轴
2.位置与开口方向
3.增减性与最值
抛物线
顶点坐标
对称轴
位置
开口方向
增减性
最值
y=x2
y= -x2
(0,0)
(0,0)
y轴
y轴
在x轴的上方(除顶点外)
在x轴的下方( 除顶点外)
向上
向下
当x=0时,最小值为0.
当x=0时,最大值为0.
在对称轴的左侧,y随着x的增大而减小. 在对称轴的右侧, y随着x的增大而增大.
在对称轴的左侧,y随着x的增大而增大. 在对称轴的右侧, y随着x的增大而减小.
根据图形填表:
y=x2和y=-x2是y=ax2当a=±1时的特殊例子.a的符号确定着抛物线的……
函数y=ax2(a≠0)的图象和性质:
在同一坐标系中作出函数y=x2和y=-x2的图象
y=x2
y=-x2
1.抛物线y=ax2的顶点是原点,对称轴是y轴.
2.当a>0时,抛物线y=ax2在x轴的上方(除顶点外),它的开口向上,并且向上无限伸展; 当a<0时,抛物线y=ax2在x轴的下方(除顶点外),它的开口向下,并且向下无限伸展.
3.当a>0时,在对称轴的左侧,y随着x的增大而减小;在对称轴右侧,y随着x的增大而增大.当x=0时函数y的值最小.当a<0时,在对称轴的左侧,y随着x的增大而增大;在对称轴的右侧,y随着x增大而减小,当x=0时,函数y的值最大.
二次函数y=ax2的性质
我思,我进步
1.已知抛物线y=ax2经过点A(-2,-8).
(1)求此抛物线的函数解析式;
(2)判断点B(-1,- 4)是否在此抛物线上.
(3)求出此抛物线上纵坐标为-6的点的坐标.
解:(1)把(-2,-8)代入y=ax2,得 -8=a(-2)2,
解得a= -2,所求函数解析式为y= -2x2.
1.抛物线y=2x2的顶点坐标是 ,对称轴是 .在 侧,y随着x的增大而增
大;在 侧,y随着x的增大而减小,当x= 时,函数y的值最小,最小值是 ,抛物线y=2x2在x轴的 方(除顶点外).
2.抛物线 在x轴的 方(除顶点外),在对称轴的左侧,y随着x的 ;在对称轴的右侧,y随着x的 ,当x=0时,函数y的值最大,最大值是 ,当x 时,y<0.
(0,0)
y轴
对称轴的右
对称轴的左
0
0
上
下
增大而增大
增大而减小
0
【跟踪训练】
回味无穷
2.当a>0时,抛物线y=ax2在x轴的上方(除顶点外),它的开口 向上,并且向上无限伸展;当a<0时,抛物线y=ax2在x轴的下方(除顶点外),它的开口向下,并且向下无限伸展.
3.当a>0时,在对称轴的左侧,y随着x的增大而减小;在对称轴 右侧,y随着x的增大而增大.当x=0时函数y的值最小.
当a<0时,在对称轴的左侧,y随着x的增大而增大;在对称轴的右侧,y随着x增大而减小,当x=0时,函数y的值最大
1.抛物线y=ax2的顶点是原点,对称轴是y轴.
由二次函数y=x2和y=-x2知:
2.2二次函数的图象与性质
(第2课时)
你能用配方的方法把y=3x2-6x+5变形成y=3(x-1)2+2的形式吗?
二次函数y=ax?+bx+c的图象
二次函数y=3x2-6x+5的图象是什么形状?它与我们已经作过的二次函数的图象有什么关系?
在同一坐标系中作出二次函数y=3x2和y=3(x-1)2的图象.
由于y=3x2-6x+5=3(x-1)2+2,因此我们先作二次函数y=3(x-1)2的图象.
比较函数 与 的图象
(2)在同一坐标系中作出二次函数y=3x2和y=3(x-1)2的图象.
⑴完成下表,并比较3x2和3(x-1)2的值,它们之间有什么关系?
x -3 -2 -1 0 1 2 3 4
27 12 3 0 3 12 27 48
27 12 3 0 3 12 27 48
48 27 12 3 0 3 12 27
观察图象,回答问题
(3)函数y=3(x-1)2的图象与y=3x2的图象有什么关系?它是轴对称图形吗?它的对称轴和顶点坐标分别是什么?
(4)x取哪些值时,函数y=3(x-1)2的值随x值的增大而增大?x取哪些值时,函数y=3(x-1)2的值随x的增大而减少?
图象是轴对称图形
对称轴是平行于
y轴的直线:x=1.
顶点坐标
是点(1,0).
二次函数y=3(x-1)2
与y=3x2的图象形状
相同,可以看作是抛
物线y=3x2整体沿x轴
向右平移了1 个单位
(3)函数y=3(x-1)2的图象与y=3x2的图象有什么关系?它是轴对称图形吗?它的对称轴和顶点坐标分别是什么?
二次项系数相同
a>0,开口都向上.
想一想,在同一坐标系中作二次函数y=3(x+1)2的图象,会在什么位置?
在对称轴(直线:x=1)左侧
(即x<1时),函数y=3(x-1)2
的值随x的增大而减少,.
顶点是最低点,函数
有最小值.当x=1时,
最小值是0..
二次函数y=3(x-1)2
与y=3x2的增减性类似.
(4)x取哪些值时,函数y=3(x-1)2的值随x值的增大而增大?x取哪些值时,函数y=3(x-1)2的值随x的增大而减少?
在对称轴(直线:x=1)左侧
(即x>1时),函数y=3(x-1)2
的值随x的增大而增大,.
想一想,在同一坐标系中作出二次函数y=3(x+1)2的图象,它的增减性会是什么样?
真知 从实践走来
1.在上面的坐标系中作出二次函数y=3(x+1)2的图象.它与二次函数y=3x2和y=3(x-1)2的图象有什么关系?它是轴对称图形吗?它的对称轴和顶点坐标分别是什么?
2.x取哪些值时,函数y=3(x+1)2的值随x值的增大而增大?x取哪些值时,函数y=3(x+1)2的值随x的增大而减少?
在同一坐标系中作出二次函数y=3x2,y=3(x-1)2和y=3(x+1)2的图象.
完成下表,并比较3x2,3(x-1)2和3(x+1)2的值,它们之间有什么关系?
函数y=a(x-h)2(a≠0)的图象和性质
x -4 -3 -2 -1 0 1 2 3 4
27 12 3 0 3 12 27
27 12 3 0 3 12 27
27 12 3 0 3 12 27
27 12 3 0 3 12 27
图象是轴对称图形.
对称轴是平行于
y轴的直线:x= -1.
顶点坐标
是点(-1,0).
二次函数y=3(x+1)2
与y=3x2的图象形状
相同,可以看作是抛
物线y=3x2整体沿x轴
向左平移了1 个单位.
1.函数y=3(x+1)2的图象与y=3x2和y=3(x-1)2的图象有什么关系?它是轴对称图形吗?它的对称轴和顶点坐标分别是什么?
二次项系数相同
a>0,开口都向上.
想一想,二次函数y=3(x+1)2的图象的增减性会怎样?
在对称轴(直线:x=-1)左侧
(即x<-1时),函数y=3(x+1)2
的值随x的增大而减少,.
顶点是最低点,函数
有最小值.当x=-1时,
最小值是0..
二次函数y=3(x+1)2
与y=3x2的增减性类似.
2.x取哪些值时,函数y=3(x+1)2的值随x值的增大而增大?x取哪些值时,函数y=3(x+1)2的值随x的增大而减少?
在对称轴(直线:x=-1)右侧
(即x>-1时),函数y=3(x+1)2
的值随x的增大而增大,.
猜一猜,函数y=-3(x-1)2,y=-3(x+1)2和y=-3x2的图象的位置和形状.
请你总结二次函数y=a(x-h)2的图象和性质.
www.1230.org 初中数学资源网
2.抛物线y=-3(x-1)2和y=-3(x+1)2在x轴的下方(除顶点外),它的开口向下,并且向下无限伸展.
3.抛物线y=-3(x-1)2在对称轴(x=1)的左侧,当x<1时, y随着x的增大而增大;在对称轴(x=1)右侧,当x>1时, y随着x的增大而减小.当x=1时,函数y的值最大(是0);
抛物线y=-3(x+1)2在对称轴(x=-1)的左侧,当x<-1时, y随着x的增大而增大;在对称轴(x=-1)右侧,当x>-1时, y随着x的增大而减小.当x=-1时,函数y的值最大(是0).
二次函数y=-3(x-1)2,y=-3(x+1)2和y=-3x2的图象
4.抛物线y=-3(x-1)2可以看作是抛物线y=-3x2沿x轴向右平移了1个单位;抛物线y=-3(x+1)2可以看作是抛物线y=-3x2沿x轴向左平移了1个单位.
X=-1
X=1
1.抛物线y=-3(x-1)2的顶点是(1,0);对称轴是直线:x=1;抛物线y=-3(x+1)2的顶点是(-1,0);对称轴是直线:x=-1.
www.1230.org 初中数学资源网
1.抛物线y=a(x-h)2的顶点是(h,0),对称轴是平行于y轴的直线x=h.
3.当a>0时,在对称轴(x=h)的左侧,y随着x的增大而减小;在对称轴(x=h)右侧,y随着x的增大而增大;当x=h时函数y的值最小(是0).
当a<0时,在对称轴(x=h)的左侧,y随着x的增大而增大;在对称轴(x=h)的右侧,y随着x增大而减小;当x=h时,函数y的值最大(是0).
二次函数y=a(x-h)2的性质
2.当a>0时,抛物线y=a(x-h)2在x轴的上方(除顶点外),它的开口向上,并且向上无限伸展;
当a<0时,抛物线y=a(x-h)2在x轴的下方(除顶点外),它的开口向下,并且向下无限伸展.
X=h
X=h
二次函数y=a(x-h)2的性质
1.顶点坐标与对称轴
2.位置与开口方向
3.增减性与最值
抛物线
顶点坐标
对称轴
位置
开口方向
增减性
最值
y=a(x-h)2 (a>0)
y=a(x-h)2 (a<0)
(h,0)
(h,0)
直线x=h
直线x=h
在x轴的上方(除顶点外)
在x轴的下方( 除顶点外)
向上
向下
当x=h时,最小值为0.
当x=h时,最大值为0.
在对称轴的左侧,y随着x的增大而减小. 在对称轴的右侧, y随着x的增大而增大.
在对称轴的左侧,y随着x的增大而增大. 在对称轴的右侧, y随着x的增大而减小.
根据图形填表:
开口大小
我思,我进步
在同一坐标系中作出二次函数y=3x?,y=3(x-1)2和y=3(x-1)2+2的图象.
二次函数y=3x?,y=3(x-1)2和y=3(x-1)2+2的图象有什么关系?它们的开口方向,对称轴和顶点坐标分别是什么?作图看一看.
在同一坐标系中作出函数y=3x?,y=3(x-1)2和y=3(x-1)2+2的图象.
完成下表,并比较3x2,3(x-1)2和3(x-1)2+2值,它们之间有何关系?
函数y=a(x-h)2+k(a≠0)的图象和性质
x -4 -3 -2 -1 0 1 2 3 4
27 12 3 0 3 12 27
27 12 3 0 3 12 27
27 12 3 0 3 12 27
29 14 5 2 5 14 29
对称轴仍是平行于y轴的直
线(x=1);增减性与y=3x2类似.
顶点是(1,2).
二次函数y=3(x-1)2+2的
图象可以看作是抛物线
y=3x2先沿着x轴向右平移
1个单位,再沿直线x=1向
上平移2个单位后得到的.
二次函数y=3(x-1)2+2的图象和抛物线y=3x?,y=3(x-1)2有什么关系?它的开口方向,对称轴和顶点坐标分别是什么?
开口向上,当
X=1时有最小
值:且最小值=2.
先猜一猜,再做一做,在同一坐标系中作二次函数y=3(x-1)2-2,会是什么样?
X=1
对称轴仍是平行于y轴的直线
(x=1);增减性与y=3x2类似.
顶点是(1,-2).
二次函数y=3(x-1)2-2的
图象可以看作是抛物线
y=3x2先沿着x轴向右平移
1个单位,再沿直线x=1向
下平移2个单位后得到的.
二次函数y=3(x-1)2-2的图象与抛物线y=3x2和y=3(x-1)2有何关系?它的开口方向、对称轴和顶点坐标分别是什么?
开口向上,
当x=1时y有
最小值:且
最小值= -2.
想一想,二次函数y=-3(x-1)2+2和y=-3x?,y=-3(x-1)2的图象有什么关系?它们的开口方向,对称轴和顶点坐标分别是什么?再作图看一看.
X=1
我思,我进步
在同一坐标系中作出二次函数y=-3(x-1)2+2,y=-3(x-1)2-2,y=-3x?和y=-3(x-1)2的图象
二次函数y=-3(x-1)2+2与y=-3(x-1)2-2和y=-3x?,y=-3(x-1)2的图象有什么关系?它们是轴对称图形吗?它的开口方向、对称轴和顶点坐标分别是什么?当x取哪些值时,y的值随x值的增大而增大?当x取哪些值时,y的值随x值的增大而减小?
对称轴仍是平行于y轴的直线
(x=1);增减性与y= -3x2类似.
顶点分别是
(1,2)和(1,-2).
二次函数y=-3(x-1)2+2与
y=-3(x-1)2+2的图象可
以看作是抛物线y=-3x2
先沿着x轴向右平移1个
单位,再沿直线x=1向上
(或向下)平移2个单位后
得到的.
二次函数y=-3(x-1)2+2与y=-3(x-1)2-2的图象和抛物线y=-3x?,y=-3(x-1)2有什么关系? 它的开口方向,对称轴和顶点坐标分别是什么?
想一想,二次函数y=-3(x+1)2+2与y=-3(x+1)2-2的图象和抛物线y=-3x?,y=-3(x+1)2
y
X=1
对称轴仍是平行于y轴的直线
(x=-1);增减性与y= -3x2类似.
顶点分别是
(-1,2)和(-1,-2)..
二次函数y=-3(x+1)2+2与
y=-3(x+1)2-2的图象可
以看作是抛物线y=-3x2
先沿着x轴向左平移1个
单位,再沿直线x=-1向上
(或向下)平移2个单位后
得到的.
二次函数y=-3(x-1)2+2与y=-3(x-1)2-2的图象和抛物线y=-3x?,y=-3(x-1)2有什么关系? 它的开口方向,对称轴和顶点坐标分别是什么?
开口向下,
当x=-1时y有
最大值:且
最大值= 2
(或最大值=-2).
先想一想,再总结二次函数y=a(x-h)2+k的图象和性质.
X=1
一般地,由y=ax?的图象便可得到二次函数y=a(x-h)?+k的图象:y=a(x-h)?+k(a≠0) 的图象可以看成y=ax?的图象先沿x轴整体左(右)平移|h|个单位(当h>0时,向右平移;当h<0时,向左平移),再沿对称轴整体上(下)平移|k|个单位 (当k>0时向上平移;当k<0时,向下平移)得到的.
因此,二次函数y=a(x-h)?+k的图象是一条抛物线,它的开口方向、对称轴和顶点坐标与a,h,k的值有关.
二次函数y=a(x-h)?+k与=ax?的关系
在对称轴的左侧,y随着x的增大而增大. 在对称轴的右侧, y随着x的增大而减小.
二次函数y=a(x+h)2+k的图象和性质
1.顶点坐标与对称轴
2.位置与开口方向
3.增减性与最值
抛物线
顶点坐标
对称轴
位置
开口方向
增减性
最值
y=a(x-h)2+k(a>0)
y=a(x-h)2+k(a<0)
(-h,k)
(-h,k)
直线x=h
直线x=h
由h和k的符号确定
由h和k的符号确定
向上
向下
当x=h时,最小值为k.
当x=h时,最大值为k.
在对称轴的左侧,y随着x的增大而减小. 在对称轴的右侧, y随着x的增大而增大.
根据图形填表:
1.相同点: (1)形状相同(图像都是抛物线,开口方向相同).
(2)都是轴对称图形.
(3)都有最(大或小)值.
(4)a>0时, 开口向上,在对称轴左侧,y都随x的增大而减小,在对称轴右侧,y都随 x的增大而增大. a<0时,开口向下,在对称轴左侧,y都随x的增大而增大,在对称轴右侧,y都随 x的增大而减小 .
2.不同点: 只是位置不同(1)顶点不同:分别是(-h,k)和(0,0).
(2)对称轴不同:分别是直线x= -h和y轴.
(2)最值不同:分别是k和0.
3.联系: y=a(x-h)?+k(a≠0) 的图象可以看成y=ax?的图象先沿x轴整体左(右)平移|h|个单位(当h>0时,向右平移;当h<0时,向左平移),再沿对称轴整体上(下)平移|k|个单位 (当k>0时向上平移;当k<0时,向下平移)得到的.
回味无穷
二次函数y=a(x-h)?+k与=ax?的关系
1.下列二次函数中,图象以直线x=2为对称轴、且经过点(0,1)的是( ).
A.y=(x-2)2+1 B.y=(x+2)2+1
C.y=(x-2)2-3 D.y=(x+2)2-3
【解析】选C.根据以直线x=2为对称轴可知选项A,C符合,再根据图象经过点(0,1)知选项C符合.
2.将抛物线
向左平移1个单位后所得到的新抛物线的表达式为
_______________.
【答案】
3.将抛物线 先向上平移2个单位,再向右平移1个单位后,得到的抛物线的表达式为____________.
【答案】
【答案】选B.
4.把抛物线 向左平
移1个单位,然后向上平移3个单位,则平移后抛物线的表达式为( )
B.
C.
D.
A.
2.2二次函数的图象与性质
(第3课时)
1.指出下列二次函数的开口方向、对称轴和顶点坐标.
(1) y=2(x-3)2 -5
(2)y=-0.5(x+1)2
(3) y = 3(x+4)2+2
2.它们分别可以看成是由哪个函数图象通过怎样的平移得到的?
复习引入:
我们知道,作出二次函数y=3x2的图象,通过平移抛物线y=3x2可以得到二次函数y=3x2-6x+5的图象.
那是怎样平移的呢?
y=3x2-6x+5
=3(x-1)2+2
只要将表达式右边进行配方就可以知道了.
配方后的表达式通常称为配方式或顶点式
这个结果通常称为顶点坐标公式.
二次函数y=ax?+bx+c的顶点式
【探究新知】
因此,二次函数y=ax?+bx+c的图象是一条抛物线.
结论 顶点坐标公式
根据公式确定下列二次函数图象的对称轴和顶点坐标:
【跟踪训练】
如图,桥梁的两条钢缆具有相同的抛物线形状.按照图中的直角坐标系,左面的一条抛物线可以用y= x?+ x+10
表示,而且左、右两条抛物线关于y轴对称.
⑴钢缆的最低点到桥面的距离是多少?
⑵两条钢缆最低点之间的距离是多少?
你有哪些计算方法?与同伴进行交流.
【例题】
⑴.钢缆的最低点到桥面的距离是少?你是怎样计算的?与同伴交流.
可以将函数y=0.0225x2+0.9x+10配方,求得顶点坐标,从而获得钢缆的最低点到桥面的距离;
⑵两条钢缆最低点之间的距离是多少?你是怎样计算的?与同伴交流.
想一想,你知道图中右面钢缆的表达式是什么吗?
⑶你还有其他方法吗?与同伴交流.
直接利用顶点坐标公式再计算一下上面问题中钢缆的最低点到桥面的距离以及两条钢缆最低点之间的距离.
1. 如图为抛物线y=ax2+bx+c的图象,A , B, C 为抛物线与坐标轴的交点,且OA=OC=1,则下列关系中正确的是( )
A.a+b=-1 B.a-b=-1
C.b<2a D.ac<0
选B.∵抛物线开口向上,∴a>0, ∵抛物线与y轴交于正半轴,∴c>0,∴ac>0,故D错;∵OA=OC=1,∴A,C两点的坐标分别为(-1,0),(0,1),∴当x=0时,y=1,即c=1;当x=-1时,y=0,即a-b+c=0,∴a-b=-c=-1,故B对;由图象可知x=1时,y>0,即a+b+c>0,∴a+b>-1,故A错;
∵对称轴 ,∴b>2a,故C错.
巩固练习
2.二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列结论①a,b异号;②当x=1和x=3时,函数值相等;③4a+b=0;④当y=4时,x的取值只能为0.其中正确的个数为( )
A.1 B.2
C.3 D.4
选C.
A.0,5 B.0,1
C.-4,5 D.-4,1
,
的值分别为( )
3. 若二次函数
配方后为
则
选D.
4.已知二次函数y=ax2+bx+c的图象如图所示,则下列结论正确的是( )
A.a>0 B.c<0
C.b2-4ac<0 D.a+b+c>0
选D.
x
y
O
选D.
6.已知二次函数
(a为常数),当a取不同的值时,其图象构成一个“抛物线系”.下图分别是当a=-1, a=0, a=1, a=2时二次函数的图象.它们的顶点在同一条直线上,这条直线的解析式是 .
【规律方法】
二次函数y=ax2+bx+c(a≠0)与y=ax?(a≠0)的关系
1.相同点: (1)形状相同(图象都是抛物线,开口方向相同).
(2)都是轴对称图形.
(3)都有最大(或小)值.
(4)a>0时, 开口向上,在对称轴左侧,y随x的增大而减小;在对称轴右侧,y随 x的增大而增大.a<0时,开口向下,在对称轴左侧,y随x的增大而增大;在对称轴右侧,y随 x的增大而减小 .
2.不同点: (1)位置不同.
(2)顶点不同:分别是 和(0,0).
(3)对称轴不同:分别是 和y轴.
(4)最值不同:分别是 和 0.
3.联系: (a≠0) 的图象可以看成y=ax?的
图象先沿x轴整体左(右)平移| |个单位(当
时向右平移,当 时向左平移),再沿对称轴
整体上(下)平移| |个单位 (当 >0时
向上平移;当 <0时,向下平移)得到的.
二次函数y=ax2+bx+c(a≠0)的图象和性质
1.顶点坐标与对称轴
2.位置与开口方向
3.增减性与最值
抛物线
顶点坐标
对称轴
位置
开口方向
增减性
最值
y=ax2+bx+c(a>0)
y=ax2+bx+c(a<0)
由a,b和c的符号确定
由a,b和c的符号确定
向上
向下
在对称轴的左侧,y随x的增大而减小. 在对称轴的右侧, y随x的增大而增大.
在对称轴的左侧,y随x的增大而增大. 在对称轴的右侧, y随x的增大而减小.
根据图形填表:
结束寄语
只有不断的思考,才会有新的发现;只有量的变化,才会有质的进步.
