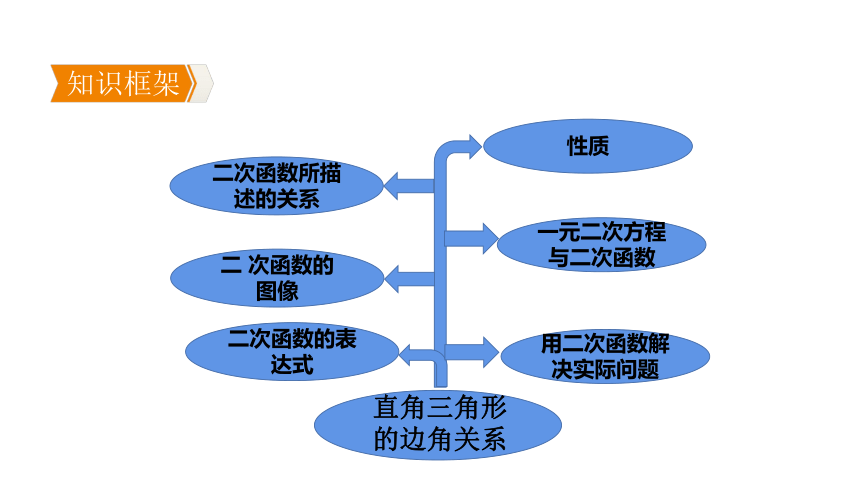
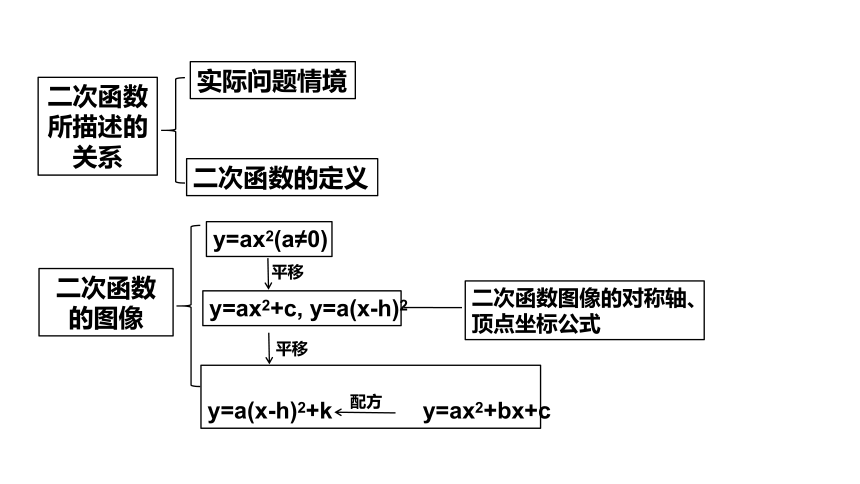
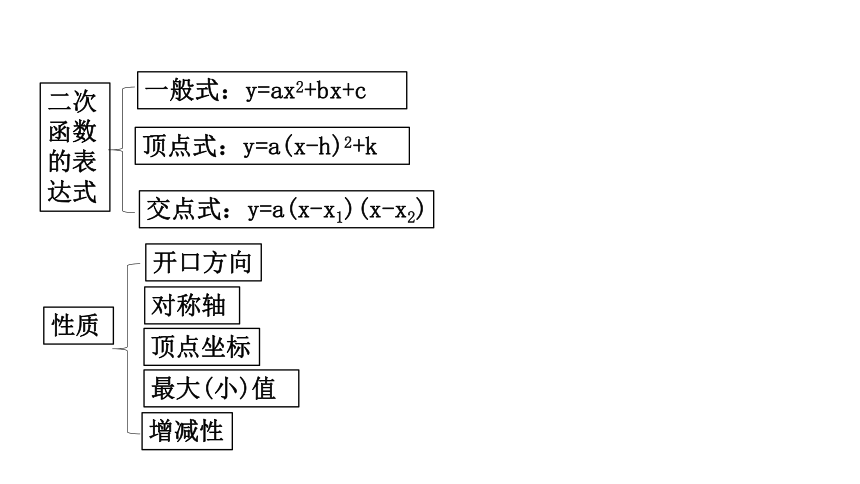
北师大版九年级数学下册第二章二次函数章末复习课件(共84张PPT)
文档属性
| 名称 | 北师大版九年级数学下册第二章二次函数章末复习课件(共84张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 2.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-02-26 17:51:12 | ||
图片预览






文档简介
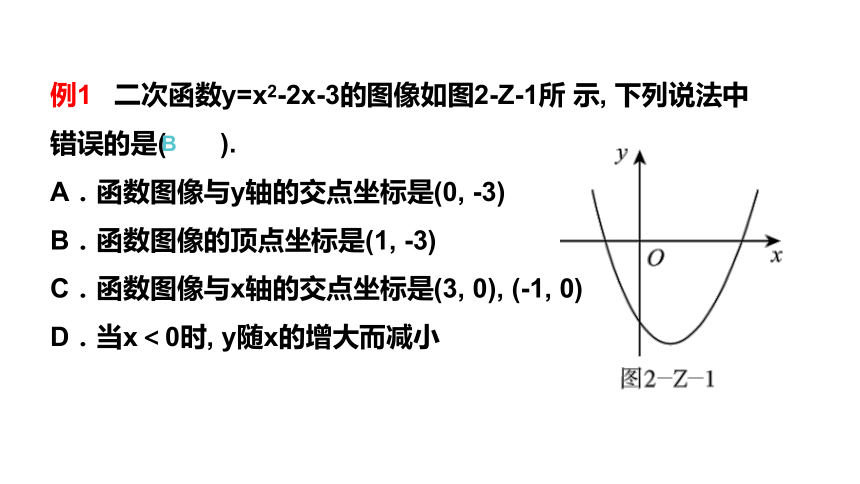
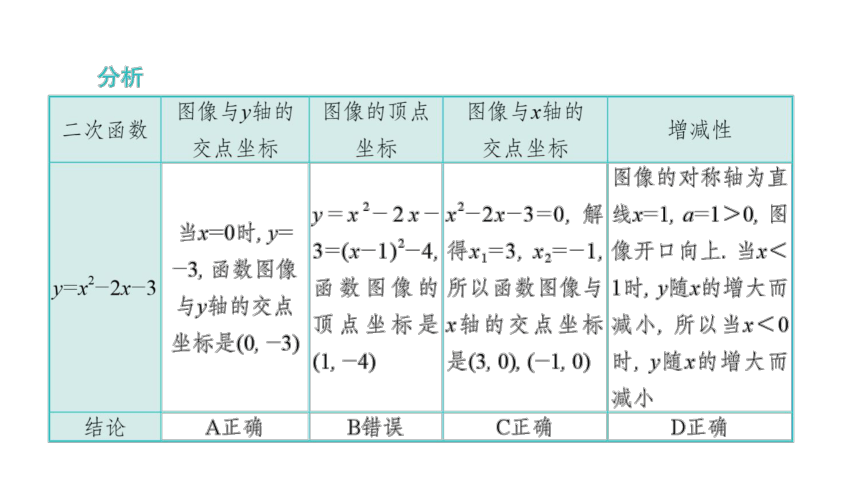
课件84张PPT。第二章 二次函数章末复习第二章 二次函数章末复习【要点指导】解决这类问题主要是理解二次函数的定义与性质. 对于二次函数的性质有时要把表达式和图像联系起来理解.专题一 二次函数的图像与性质BC解析 当a<0时,二次函数图像的顶点在y轴负半轴上,一次函数的图像经过第一、二、四象限;当a>0时,二次函数图像的顶点在y轴正半轴上,一次函数的图像经过第一、二、三象限.【要点指导】 a的值与图像的开口方向有关, 开口向上时,a>0;开口向下时, a<0. 当对称轴在y轴左侧时, a, b同号;当对称轴在y轴右侧时, a, b异号.图像与y轴的交点在y轴正半轴上时, c>0;图像与y轴的交点是原点时, c=0;图像与y轴的交点在y轴负半轴上时, c<0. 当图像与x轴有两个交点时, b2-4ac>0;当图像与x轴只有一个交点时, b2-4ac=0;当图像与x轴没有交 点时, b2-4ac<0. 专题二 二次函数y=ax2+bx+c(a≠0)的图像与系数的关系BD【要点指导】 解决这类问题常用待定系数法. 设二次函数表达式时常见的有三种形式:一般式y=ax2+bx+c(a≠0);顶点式y=
a(x-h)2+k(a≠0), 其中(h, k)是二次函数图像的顶点坐标;交点式y=a(x-x1)(x-x2)(a≠0), 其中x1, x2是抛物 线与x轴交点的横坐标.专题三 求二次函数的表达式 例3 已知抛物线y=ax2+bx+c(a≠0)与抛物线y=2x2的开口方向相反、形状相同, 顶点坐标为(3, 5).
(1)求抛物线y=ax2+bx+c的函数表达式;
(2)求抛物线y=ax2+bx+c与x轴、y轴的交点坐标. 相关题3-1 已知直线y=x-2与某抛物线相交于(2, m), (n, 3)两点, 抛物线的对称轴是直线x=3, 求抛物线的函数表达式. 解: 把(2,m)代入y=x-2,得m=2-2=0.
把(n,3)代入y=x-2,得3=n-2,得n=5,
即直线与抛物线交于(2,0),(5,3)两点.
∵抛物线的对称轴是直线x=3,∴抛物线与x轴的另一个交点坐标为(4,0).
设y=a(x-2)(x-4).
把(5,3)代入上式,得3=a×(5-2)×(5-4),
∴a=1,∴y=(x-2)(x-4)=x2-6x+8.相关题3-2 若抛物线l:y=ax2+bx+c (a≠0)与x轴交于A(-1, 0), B(4, 0)两点, 且交y轴负半轴于点C. 若OC=2, 求抛物线的表达式.【要点指导】 二次函数y=ax2+bx+c(a≠0)的图像与x轴的交点有三种情况:没有交点、有一个交点、有两个交点, 这分别对应着一元二次方程 ax2+bx+c=0(a≠0)的根的三种情况:没有实数根、有两个相等的实数根、 有两个不相等的实数根. 专题四 二次函数与一元二次方程的关系例4 若二次函数y=2(k-1)x2-4kx+2(k-1)的图像与x轴有两个不同的 交点, 求k的取值范围. B【要点指导】 解决这类问题首先要读懂题意, 找出题目中的变量和不变 量, 构造二次函数解决问题. 这类问题不仅与实际生活有密切联系, 而且还考查我们代数方面和几何方面的综合能力, 常作为压轴题出现. 专题五 二次函数的实际应用 例5 [朝阳中考]某公司设计了一款产品, 每件成本是50元, 在试销期间, 据市场调查发现, 当销售单价是60元/件时, 每天的销售量是250件, 而销售单价每增加1元, 每天会少售出5件, 公司决定销售单价x(元/件)不低于60, 而市场要求x不得超过100.
(1)求出每天的销售量y(件)与销售单价x(元/件)之间的函数关系式, 并写出x的取值范围; (2)求出每天的销售利润W(元)与销售单价x(元/件)之间的函数关系式, 并求出当销售单价为多少时, 每天的销售利润最大, 并求出最大销售利润;
(3)若该公司要求每天的销售利润不低于4000元, 但每天的总成本不超过6250元, 则销售单价最低可定为多少?解: (1)y=250-5(x-60), 即y=-5x+550(60≤x≤100).
(2)W=(x-50)(-5x+550), 即W=-5x2+800x-27 500(60≤x≤100).
配方, 得W=-5(x-80)2+4500.
∵a=-5, ∴抛物线开口向下, ∴当x=80时, W有最大值, 为4500,
即当销售单价为80元/件时, 每天的销售利润最大, 最大销售利润为 4500元.
(3)令W=4000, 则-5(x-80)2+4500=4000, 解得x1=70, x2=90.
∴当W≥4000时, x的取值范围为70≤x≤90.
∵50(-5x+550)≤6250, 解得x≥85,
∴x的取值范围为85≤x≤90, 即销售单价最低可定为85元/件. 【要点指导】数形结合思想就是在研究问题时把数与形结合起来考虑, 即把问题的数量关系转化为图形的性质, 或者把图形的性质转化为数量关系来考虑, 从而使复杂的问题简单化, 抽象的问题具体化.专题一 数形结合思想专题二 方程思想【要点指导】方程思想就是对所求问题通过列方程(组)来求解的解题策略, 方程思想在二次函数中主要体现在求二次函数的表达式.专题三 数学建模思想【要点指导】在实际问题中, 根据已知条件、公式和定理, 建立函数模型, 再根据它们的性质或图像解决问题, 这就是数学建模思想.(1)请你从所学过的一次函数、二次函数和反比例函数中确定哪种函数能表示y1与t的变化规律, 写出y1与t的函数表达式及自变量t的取值范围;
(2)分别探求该产品在国外市场上市20天前(不含第20天)与20天后(含第20天)的日销售量y2(万件)与时间t(t为整数, 单位:天)所符合的函数表达 式, 并写出相应自变量t的取值范围;
(3)设国内、外市场的日销售总量为y万件, 写出y与t的函数表达式, 并判 断上市第几天国内、外市场的日销售总量最大, 并求出此时的最大销售量. 解:(1)∵AD=EF=BC=x m, ∴AB=(18-3x)m,
∴水池的总容积为1.5x(18-3x)=36,
即x2-6x+8=0, 解得x=2或x=4.
故x应等于2或4.
(2)由(1)知V关于x的函数表达式为V=1.5x(18-3x)=-4.5x2+27x, x的取值范围是0(3)V=-4.5x2+27x=-4.5(x-3)2+40.5,
∴当x=3时, V有最大值40.5.
故若想使水池的总容积V最大,则x应为3, 最大容积为40.5 m3.A链接1 [攀枝花中考]抛物线y=x2-2x+2的顶 点坐标为( ). A.(1, 1) B.(-1, 1) C.(1, 3) D.(-1, 3) 分析 ∵y=x2-2x+2=(x-1)2+1, ∴顶点坐标为(1, 1). 故选A. 链接2 [广州中考]当x= 时, 二次函数y=x2-2x+6有最小值 .分析 ∵y=x2-2x+6=(x-1)2+5,
∴当x=1时, 二次函数y=x2-2x+6有最小值5. 15母题2 (教材P41习题2.5第2题)
将二次函数y=x2-2x+1的图像向上平移2个单位长度, 再向左平移3个单位长度, 得到抛物线 y=x2+bx+c, 求b, c的值, 并求出这条抛物线的开 口方向、对称轴和顶点坐标, 必要时画草图进行验证. 考点:二次函数图像的平移规律.
考情:二次函数图像的平移是中考的热点内容, 主要考查平移前后二次函数表达式的区别, 多以选择题的形式出现.
策略:解决二次函数图像的平移问题时, 一般先把二次函数的一般式y=ax2+bx+c(a≠0)化为顶点式 y=a(x-h)2+k(a≠0), 然后根据平移规律解决问题. D母题3 (教材P43随堂练习第1题)
已知二次函数图像的顶点坐标是(-1, 1), 且经过点(1, -3), 求这个二次函数的表达式.考点:二次函数表达式的确定.
考情:确定二次函数的表达式是中考的重要内容, 主要以解答题的形式出现, 常与其他函数或几何图形结合考查.
策略:确定二次函数的表达式的关键是根据已知条件选择适当的表达式用待定系数法求解. 当已知条件为三个点的坐标时, 一般选用一般式 y=ax2+bx+c(a≠0);当已知图像的顶点坐标时, 常选用顶点式y=a(x-h)2+k(a≠0);当已知图像与x 轴的两个交点坐标时, 常选用交点式y=a(x-x1)(x-x2)(a≠0). 链接4 [徐州中考]已知二次函数的图像以点 A(-1, 4)为顶点, 且过点B(2, -5).
(1)求该二次函数的表达式;
(2)求该二次函数图像与坐标轴的交点坐标;
(3)将该二次函数图像向右平移, 当图像经过 原点时, A, B两点随图像移至A′, B′两点, 求△O A′B′ 的面积. 分析 已知二次函数图像的顶点坐标, 可用顶 点式设该二次函数的表达式, 然后画出函数图像, 利用数形结合思想求解问题. 解: (1)设二次函数表达式为y=a(x+1)2+4. 将B(2, -5)代入, 可求得a=-1,
∴该二次函数的表达式为y=-(x+1)2+4= -x2-2x+3.
(2)令x=0, 得y=3, 因此二次函数图像与y轴的交点坐标为(0, 3).
令y=0, 得-x2-2x+3=0, 解得 x1=-3, x2=1,
即二次函数图像与x轴的交点坐标为 (-3, 0), (1, 0). 母题4 (教材P49随堂练习)
某商店购进一批单价为20元的日用商品, 如果以单价30元销售, 那么半月内可售出400件. 根据销售经验, 提高销售单价会导致销售量的减少, 即销售单价每提高1元, 销售量相应减少20件. 销售单价为多少元时, 半月内获得的利润最大?最大利润是多少?考点:二次函数的应用——求最大利润问题.
考情:利用二次函数解决通过涨价或降价获得最大利润的问题是近几年中考的热点题型, 预测今年中考会继续加强对这方面知识的考查.
策略:基本思路是先建立变量间的二次函数关 系, 再利用二次函数的有关性质求解. 链接5 [营口中考] 某商场销售A, B两款书 包, 已知A, B两款书包的进货价格分别为每个30元, 50元, 商场用3600元的资金购进A, B两款书包共 100个.
(1)求A, B两款书包分别购进多少个;
(2)经市场调查发现, B款书包每天的销售 量y(个)与销售单价x(元/个)有如下关系:y= -x+90(60≤x≤90). 设B款书包每天的销售利润 为w元, 当B款书包的销售单价为多少元/个时, 商 场每天销售B款书包的利润最大?最大利润是多少元? 解: (1)设购进A款书包x个, 则购进B款书包 (100-x)个.
由题意得30x+50(100-x)=3600, 解得x=70. 则100-x=30.
因此, A, B两款书包分别购进70个和30个.
(2)由题意得w=y(x-50)=-(x-50)(x-90)= -(x-70)2+400.
∵-1<0, ∴w有最大值. 函数图像的对称轴为直线x=70, 而60≤x≤90, 故当x=70时, w有最大值, 为400.
因此, 当B款书包的销售单价为70元/个时, 商场每天销售B款书包的利润最大, 最大利润是400元. 考点:二次函数的应用——求图形的最大面积问题.
考情:求图形的最大面积问题是中考中的热点题型, 涉及的图形主要有三角形、矩形、正方形等, 以解答题的形式为主, 题目的综合性较强. 预测今后中考会加强对该知识点的综合运用的考查.
策略:深入研究几何图形中各个量之间的关系, 准确地用含有自变量的代数式表示图中各个相 关量, 列出二次函数表达式, 然后运用二次函数的性质解决问题. 此类问题往往含有一些限制条件, 这时要特别注意自变量的取值范围, 充分考虑限制条件, 防止造成求值错误.母题6 (教材P53习题2.10第2题)
二次函数y=x2+bx-1(b为常数)的图像与x轴相交吗?如果相交, 有几个交点? 考点:二次函数与一元二次方程之间的关系.
考情:利用二次函数的图像求一元二次方程的根.
策略:求二次函数的图像与x轴的交点的横坐标, 就是求当y=0时对应一元二次方程的根. 链接8 [江西中考]已知二次函数y=x2+bx-2 的图像与x轴的一个交点坐标为(1, 0), 则它与x轴的 另一个交点坐标是( ).
A.(1, 0) B.(2, 0) C.(-2, 0) D.(-1, 0) C
谢 谢 观 看!
a(x-h)2+k(a≠0), 其中(h, k)是二次函数图像的顶点坐标;交点式y=a(x-x1)(x-x2)(a≠0), 其中x1, x2是抛物 线与x轴交点的横坐标.专题三 求二次函数的表达式 例3 已知抛物线y=ax2+bx+c(a≠0)与抛物线y=2x2的开口方向相反、形状相同, 顶点坐标为(3, 5).
(1)求抛物线y=ax2+bx+c的函数表达式;
(2)求抛物线y=ax2+bx+c与x轴、y轴的交点坐标. 相关题3-1 已知直线y=x-2与某抛物线相交于(2, m), (n, 3)两点, 抛物线的对称轴是直线x=3, 求抛物线的函数表达式. 解: 把(2,m)代入y=x-2,得m=2-2=0.
把(n,3)代入y=x-2,得3=n-2,得n=5,
即直线与抛物线交于(2,0),(5,3)两点.
∵抛物线的对称轴是直线x=3,∴抛物线与x轴的另一个交点坐标为(4,0).
设y=a(x-2)(x-4).
把(5,3)代入上式,得3=a×(5-2)×(5-4),
∴a=1,∴y=(x-2)(x-4)=x2-6x+8.相关题3-2 若抛物线l:y=ax2+bx+c (a≠0)与x轴交于A(-1, 0), B(4, 0)两点, 且交y轴负半轴于点C. 若OC=2, 求抛物线的表达式.【要点指导】 二次函数y=ax2+bx+c(a≠0)的图像与x轴的交点有三种情况:没有交点、有一个交点、有两个交点, 这分别对应着一元二次方程 ax2+bx+c=0(a≠0)的根的三种情况:没有实数根、有两个相等的实数根、 有两个不相等的实数根. 专题四 二次函数与一元二次方程的关系例4 若二次函数y=2(k-1)x2-4kx+2(k-1)的图像与x轴有两个不同的 交点, 求k的取值范围. B【要点指导】 解决这类问题首先要读懂题意, 找出题目中的变量和不变 量, 构造二次函数解决问题. 这类问题不仅与实际生活有密切联系, 而且还考查我们代数方面和几何方面的综合能力, 常作为压轴题出现. 专题五 二次函数的实际应用 例5 [朝阳中考]某公司设计了一款产品, 每件成本是50元, 在试销期间, 据市场调查发现, 当销售单价是60元/件时, 每天的销售量是250件, 而销售单价每增加1元, 每天会少售出5件, 公司决定销售单价x(元/件)不低于60, 而市场要求x不得超过100.
(1)求出每天的销售量y(件)与销售单价x(元/件)之间的函数关系式, 并写出x的取值范围; (2)求出每天的销售利润W(元)与销售单价x(元/件)之间的函数关系式, 并求出当销售单价为多少时, 每天的销售利润最大, 并求出最大销售利润;
(3)若该公司要求每天的销售利润不低于4000元, 但每天的总成本不超过6250元, 则销售单价最低可定为多少?解: (1)y=250-5(x-60), 即y=-5x+550(60≤x≤100).
(2)W=(x-50)(-5x+550), 即W=-5x2+800x-27 500(60≤x≤100).
配方, 得W=-5(x-80)2+4500.
∵a=-5, ∴抛物线开口向下, ∴当x=80时, W有最大值, 为4500,
即当销售单价为80元/件时, 每天的销售利润最大, 最大销售利润为 4500元.
(3)令W=4000, 则-5(x-80)2+4500=4000, 解得x1=70, x2=90.
∴当W≥4000时, x的取值范围为70≤x≤90.
∵50(-5x+550)≤6250, 解得x≥85,
∴x的取值范围为85≤x≤90, 即销售单价最低可定为85元/件. 【要点指导】数形结合思想就是在研究问题时把数与形结合起来考虑, 即把问题的数量关系转化为图形的性质, 或者把图形的性质转化为数量关系来考虑, 从而使复杂的问题简单化, 抽象的问题具体化.专题一 数形结合思想专题二 方程思想【要点指导】方程思想就是对所求问题通过列方程(组)来求解的解题策略, 方程思想在二次函数中主要体现在求二次函数的表达式.专题三 数学建模思想【要点指导】在实际问题中, 根据已知条件、公式和定理, 建立函数模型, 再根据它们的性质或图像解决问题, 这就是数学建模思想.(1)请你从所学过的一次函数、二次函数和反比例函数中确定哪种函数能表示y1与t的变化规律, 写出y1与t的函数表达式及自变量t的取值范围;
(2)分别探求该产品在国外市场上市20天前(不含第20天)与20天后(含第20天)的日销售量y2(万件)与时间t(t为整数, 单位:天)所符合的函数表达 式, 并写出相应自变量t的取值范围;
(3)设国内、外市场的日销售总量为y万件, 写出y与t的函数表达式, 并判 断上市第几天国内、外市场的日销售总量最大, 并求出此时的最大销售量. 解:(1)∵AD=EF=BC=x m, ∴AB=(18-3x)m,
∴水池的总容积为1.5x(18-3x)=36,
即x2-6x+8=0, 解得x=2或x=4.
故x应等于2或4.
(2)由(1)知V关于x的函数表达式为V=1.5x(18-3x)=-4.5x2+27x, x的取值范围是0
∴当x=3时, V有最大值40.5.
故若想使水池的总容积V最大,则x应为3, 最大容积为40.5 m3.A链接1 [攀枝花中考]抛物线y=x2-2x+2的顶 点坐标为( ). A.(1, 1) B.(-1, 1) C.(1, 3) D.(-1, 3) 分析 ∵y=x2-2x+2=(x-1)2+1, ∴顶点坐标为(1, 1). 故选A. 链接2 [广州中考]当x= 时, 二次函数y=x2-2x+6有最小值 .分析 ∵y=x2-2x+6=(x-1)2+5,
∴当x=1时, 二次函数y=x2-2x+6有最小值5. 15母题2 (教材P41习题2.5第2题)
将二次函数y=x2-2x+1的图像向上平移2个单位长度, 再向左平移3个单位长度, 得到抛物线 y=x2+bx+c, 求b, c的值, 并求出这条抛物线的开 口方向、对称轴和顶点坐标, 必要时画草图进行验证. 考点:二次函数图像的平移规律.
考情:二次函数图像的平移是中考的热点内容, 主要考查平移前后二次函数表达式的区别, 多以选择题的形式出现.
策略:解决二次函数图像的平移问题时, 一般先把二次函数的一般式y=ax2+bx+c(a≠0)化为顶点式 y=a(x-h)2+k(a≠0), 然后根据平移规律解决问题. D母题3 (教材P43随堂练习第1题)
已知二次函数图像的顶点坐标是(-1, 1), 且经过点(1, -3), 求这个二次函数的表达式.考点:二次函数表达式的确定.
考情:确定二次函数的表达式是中考的重要内容, 主要以解答题的形式出现, 常与其他函数或几何图形结合考查.
策略:确定二次函数的表达式的关键是根据已知条件选择适当的表达式用待定系数法求解. 当已知条件为三个点的坐标时, 一般选用一般式 y=ax2+bx+c(a≠0);当已知图像的顶点坐标时, 常选用顶点式y=a(x-h)2+k(a≠0);当已知图像与x 轴的两个交点坐标时, 常选用交点式y=a(x-x1)(x-x2)(a≠0). 链接4 [徐州中考]已知二次函数的图像以点 A(-1, 4)为顶点, 且过点B(2, -5).
(1)求该二次函数的表达式;
(2)求该二次函数图像与坐标轴的交点坐标;
(3)将该二次函数图像向右平移, 当图像经过 原点时, A, B两点随图像移至A′, B′两点, 求△O A′B′ 的面积. 分析 已知二次函数图像的顶点坐标, 可用顶 点式设该二次函数的表达式, 然后画出函数图像, 利用数形结合思想求解问题. 解: (1)设二次函数表达式为y=a(x+1)2+4. 将B(2, -5)代入, 可求得a=-1,
∴该二次函数的表达式为y=-(x+1)2+4= -x2-2x+3.
(2)令x=0, 得y=3, 因此二次函数图像与y轴的交点坐标为(0, 3).
令y=0, 得-x2-2x+3=0, 解得 x1=-3, x2=1,
即二次函数图像与x轴的交点坐标为 (-3, 0), (1, 0). 母题4 (教材P49随堂练习)
某商店购进一批单价为20元的日用商品, 如果以单价30元销售, 那么半月内可售出400件. 根据销售经验, 提高销售单价会导致销售量的减少, 即销售单价每提高1元, 销售量相应减少20件. 销售单价为多少元时, 半月内获得的利润最大?最大利润是多少?考点:二次函数的应用——求最大利润问题.
考情:利用二次函数解决通过涨价或降价获得最大利润的问题是近几年中考的热点题型, 预测今年中考会继续加强对这方面知识的考查.
策略:基本思路是先建立变量间的二次函数关 系, 再利用二次函数的有关性质求解. 链接5 [营口中考] 某商场销售A, B两款书 包, 已知A, B两款书包的进货价格分别为每个30元, 50元, 商场用3600元的资金购进A, B两款书包共 100个.
(1)求A, B两款书包分别购进多少个;
(2)经市场调查发现, B款书包每天的销售 量y(个)与销售单价x(元/个)有如下关系:y= -x+90(60≤x≤90). 设B款书包每天的销售利润 为w元, 当B款书包的销售单价为多少元/个时, 商 场每天销售B款书包的利润最大?最大利润是多少元? 解: (1)设购进A款书包x个, 则购进B款书包 (100-x)个.
由题意得30x+50(100-x)=3600, 解得x=70. 则100-x=30.
因此, A, B两款书包分别购进70个和30个.
(2)由题意得w=y(x-50)=-(x-50)(x-90)= -(x-70)2+400.
∵-1<0, ∴w有最大值. 函数图像的对称轴为直线x=70, 而60≤x≤90, 故当x=70时, w有最大值, 为400.
因此, 当B款书包的销售单价为70元/个时, 商场每天销售B款书包的利润最大, 最大利润是400元. 考点:二次函数的应用——求图形的最大面积问题.
考情:求图形的最大面积问题是中考中的热点题型, 涉及的图形主要有三角形、矩形、正方形等, 以解答题的形式为主, 题目的综合性较强. 预测今后中考会加强对该知识点的综合运用的考查.
策略:深入研究几何图形中各个量之间的关系, 准确地用含有自变量的代数式表示图中各个相 关量, 列出二次函数表达式, 然后运用二次函数的性质解决问题. 此类问题往往含有一些限制条件, 这时要特别注意自变量的取值范围, 充分考虑限制条件, 防止造成求值错误.母题6 (教材P53习题2.10第2题)
二次函数y=x2+bx-1(b为常数)的图像与x轴相交吗?如果相交, 有几个交点? 考点:二次函数与一元二次方程之间的关系.
考情:利用二次函数的图像求一元二次方程的根.
策略:求二次函数的图像与x轴的交点的横坐标, 就是求当y=0时对应一元二次方程的根. 链接8 [江西中考]已知二次函数y=x2+bx-2 的图像与x轴的一个交点坐标为(1, 0), 则它与x轴的 另一个交点坐标是( ).
A.(1, 0) B.(2, 0) C.(-2, 0) D.(-1, 0) C
谢 谢 观 看!
