2.2.3 二次函数y=ax^2与y=a(x-h)^2的图象和性质课件
文档属性
| 名称 | 2.2.3 二次函数y=ax^2与y=a(x-h)^2的图象和性质课件 |  | |
| 格式 | zip | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-02-27 11:33:53 | ||
图片预览




文档简介
(共26张PPT)
数学北师大版
九年级
二次函数的图象与性质
第3课时 y=ax2与y=a(x-h)2的二次函数的图象和性质.
1.函数 的图象的顶点坐标是 ;
开口方向是 ;最 值是 .
2.函数y=-2x2+3的图象可由函数y=-2x2的图象向 平移 个单位得到.
3.把函数y=-3x2的图象向下平移2个单位可得到函数
__________的图象.
(0,3)
向上
小
3
上
3
y=-3x2-2
二次函数y=ax2与y=ax2+c的图象有什么关系?
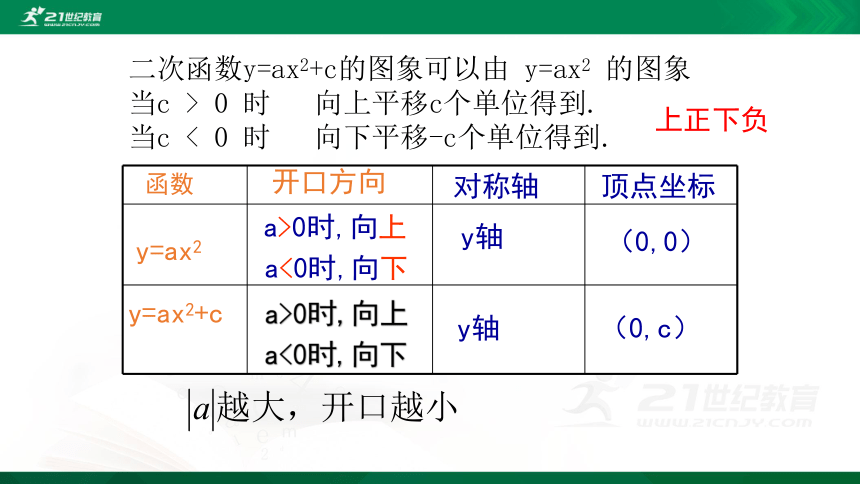
二次函数y=ax2+c的图象可以由 y=ax2 的图象
当c > 0 时 向上平移c个单位得到.
当c < 0 时 向下平移-c个单位得到.
函数
y=ax2+c
y=ax2
开口方向
a>0时,向上
a<0时,向下
对称轴
y轴
y轴
顶点坐标
(0,0)
(0,c)
a>0时,向上
a<0时,向下
上正下负
1、完成下表
x -3 -2 -1 0 1 2 3 4
y=3x?
y=3(x-1)?
27 12 3 0 3 12 27
函数y=3(x-1)?的图像是什么?
它与y=3x?的图像有什么关系?
比较y=3x?和y=3(x-1)?的值,它们之间有什么关系?
y=3(x-1)?的值比y=3x?的值落后
想一想:
27
27
12
12
3
3
0
0
12
12
27
27
新知导入
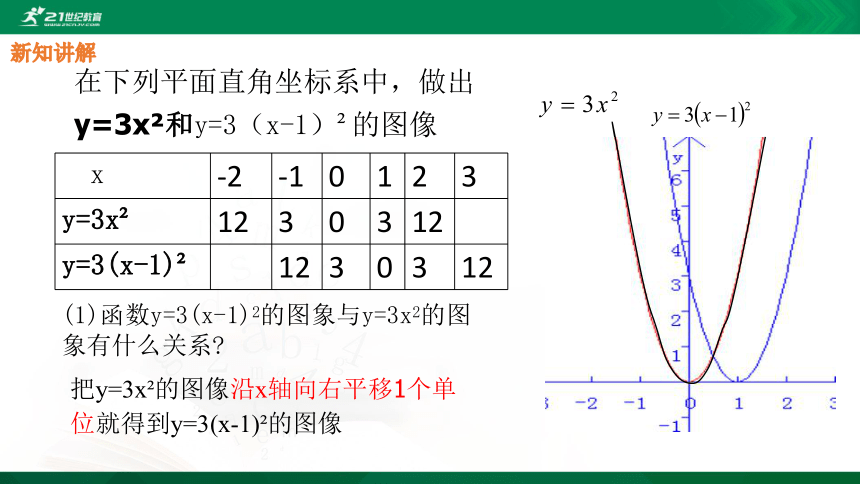
在下列平面直角坐标系中,做出y=3x?和y=3(x-1)?的图像
x -2 -1 0 1 2 3
y=3x? 12 3 0 3 12
y=3(x-1)? 12 3 0 3 12
(1)函数y=3(x-1)2的图象与y=3x2的图象有什么关系?
把y=3x?的图像沿x轴向右平移1个单位就得到y=3(x-1)?的图像
新知讲解
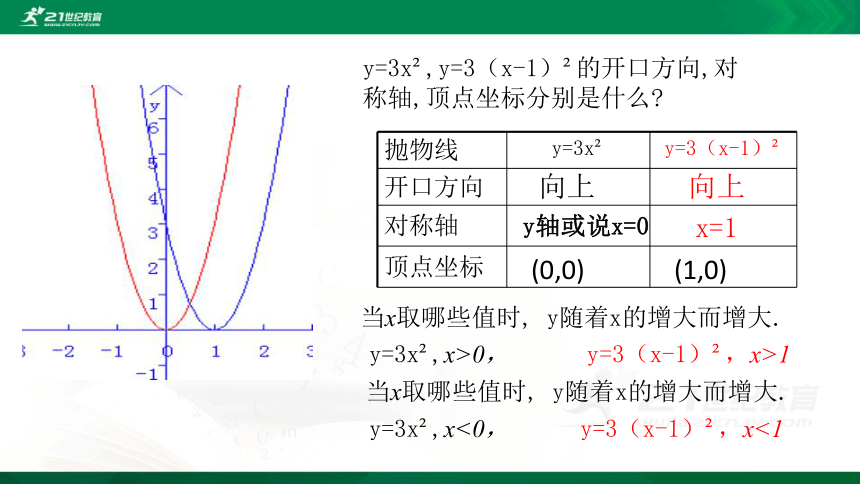
y=3x?,y=3(x-1)?的开口方向,对称轴,顶点坐标分别是什么?
抛物线 y=3x? y=3(x-1)?
开口方向
对称轴
顶点坐标
向上
向上
y轴或说x=0
x=1
(0,0)
(1,0)
当x取哪些值时, y随着x的增大而增大.
当x取哪些值时, y随着x的增大而增大.
y=3x?,x>0,
y=3(x-1)?,x>1
y=3x?,x<0,
y=3(x-1)?,x<1
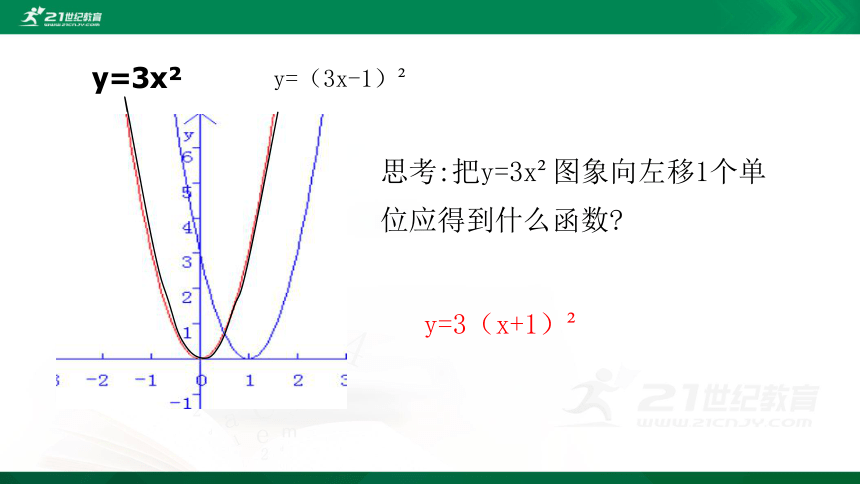
思考:把y=3x?图象向左移1个单位应得到什么函数?
y=(3x-1)?
y=3x?
y=3(x+1)?
y=(3x-1)?
y=3x?
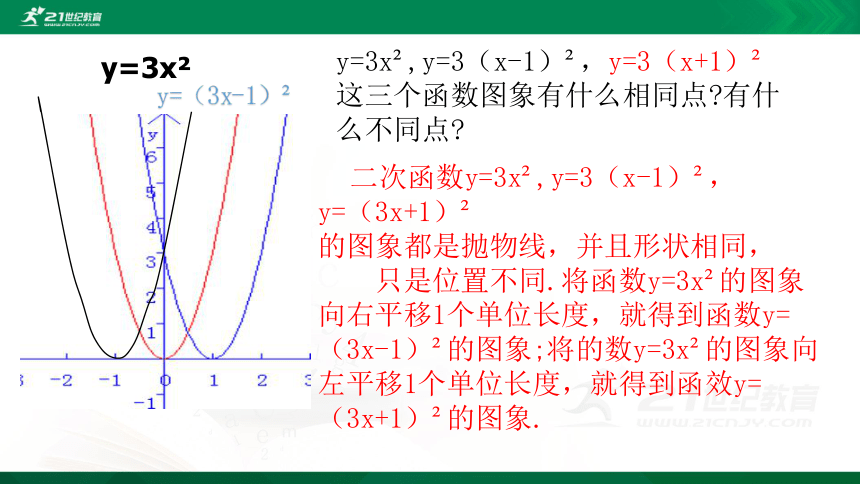
y=3x?,y=3(x-1)?,y=3(x+1)?
这三个函数图象有什么相同点?有什么不同点?
二次函数y=3x?,y=3(x-1)?,
y=(3x+1)?
的图象都是抛物线,并且形状相同,
只是位置不同.将函数y=3x?的图象向右平移1个单位长度,就得到函数y=(3x-1)?的图象;将的数y=3x?的图象向左平移1个单位长度,就得到函效y=(3x+1)?的图象.
将函数 y=2x?的图象向右平移1个单位, 就得到 y=2(x-1)?的图象;
若向左平移2个单位,得到函数 y=2(x+1)?的图象.
相同点: (1)图像都是抛物线,形状、大小相同,开口方向相同.
(2)都是轴对称图形.
(3)顶点都是最低点.
(4) 在对称轴左侧,都随 x 的增大而减小,在对称轴 右侧,都随 x 的增大而增大.
(5)它们的增长速度相同.
不同点: (1)对称轴不同. (2)顶点不同.
比较y=2x?, y=2(x-1)?,y=2(x+1)?的图象;
(6)最小值不同.
可得到函数y=a(x-h)2的图象
对称轴是直线x=h ;
顶点是(h ,0)
函数y=ax2的图象
向右平移h(h﹥0)个单位
(向左平移︱h︱(h﹤0)个单位)
函数y=a(x-h)2的图象:
0
x
y
(h ,0)
函数y=ax2与y=a(x-h)2的图象关系:
【归纳小结】
(h ,0)
左加右减
1.抛物线y=3x2-4与抛物线y =3x2 的_______相同,
_________不同.
2.抛物线y =3(x-1)2与抛物线y =3x2 的______相同,
_________不同.
3.抛物线y =3x2+5的开口_______,对称轴是______,
顶点坐标是____________.
4.抛物线y =-2(x+1)2的开口__________,对称轴是___________,顶点坐标是_____________.
形状
形状
位置
位置
向上
向下
y 轴
直线x =-1
(0,5)
(-1,0)
【跟踪训练】
5.将抛物线y=-x2向左平移2个单位后,得到的抛物线的解析式是( ).
o
y
x
1、画出二次函数y=3(x-1)2+2的图象,
2、并与二次函数y=3x2的图象进行比较,说明它们之间的关系.
函数y=3x2 的图象
向上平移
2个单位
函数y=3x2+2 的图象
向右平移
1个单位
向右平移
1个单位
函数y=3(x-1)2 的图象
向上平移
2个单位
函数y=3(x-1)2 +2的图象
再看下课本上的:在同一坐标系中作出二次函数y=2x?-1/2, y=2(x+3)2和y=2(x+3)2-1/2的图象.
二次函数y=2x?-1/2 , y=2(x+3)2和y=2(x+3)2-1/2的图象有什么关系?它们的开口方向,对称轴和顶点坐标分别是什么?
1.
2.
3.
-1
-2
-3.
0.
1.
2.
3.
4.
-1
x
y
5
y=2(x+3)2
y=2x2
y=2(x+3)2 -1/2
1.
2.
3.
-1
-2
-3.
0.
1.
2.
3.
4.
-1
x
y
5
y=2(x+3)2
y=2x2
y=2(x+3)2 -1/2
函数y=3x?的图象
o
y
x
向上平移2个单位
向右平移1个单位
练一练: 由二次函数y=3x?的图象,你能得到二次函数y=3x?+2,
y=3(x-1)?,y=3(x-2)?-5的图象吗?
y=3x?+2的图象
y=(3x-1)?的图象
y=3x?向右移平移2个单位,
再向下平移5个单位
可得y=3(x-2)?-5的图象
y=3x?向下平移5个单位
再向右移平移2个单位,
可得y=3(x-2)?-5的图象
对称轴:直线x= h
顶点: (h,k)
【规律方法】
(当k,h都大于0时)的图象特点
y=ax2的图象
向右平移
h个单位
y=a(x-h)2的图象
向上平移
k 个单位
y=a(x-h)2+k的图象
y=ax2+k的图象
向上平移
k 个单位
向右平移
h个单位
y=a(x-h)2+k的图象一条抛物线,
a>0开口向上,a<0开口向下
议一议:二次函数y=a(x-h)2+k 的图象与y=ax2 有什么关系?
y=ax2+bx+c的二次函数平移时,a的大小不会变
顶点坐标
对称轴
开口方向
抛物线
向上
向上
向上
向上
向上
向下
向下
y 轴(或x=0)
y 轴(x=0)
直线x=-1
直线x=1
直线x=1
直线x=-1
直线x=h
(h ,k)
(1,2)
(-1,-2)
(1,-2)
(-1,2)
(0,2)
(0,0)
【跟踪训练】
y=x2
y=3x2
y=5x2+2
y=(x-1)2+2
y=2(x+1)2+2
y=-(x-1)2+2
y=a(x-h)2+k
(a<0)
y=a(x-h)2+k 开口方向 对称轴 顶点坐标
a>0
a<0
向上
直线x=h
(h,k)
向下
直线x=h
(h,k)
1.y=a(x-h)2+k的图象的特征.
2.y=a(x-h)2+k的图象与y=ax2的图象的关系.
上加下减
左加右减
抛物线 有如下特点:
(1)当 a>0 时,开口向上;当 a<0 时,开口向下.
(2)对称轴为直线 x = h.
(3)顶点坐标(h,k).
(4)如果 a>0,当 x<h 时,y 随 x 的增大而减小,当 x>h 时,y 随 x 的增大而增大;
如果 a<0,当 x<h 时,y 随 x 的增大而增大,当 x>h 时,y 随 x 的增大而减小.
(5)当 a>0 时,y 有最小值k(即y ≥k);当 a<0 时,y 有最大值k(即y ≤k)
y = a(x - h)2 + k
课后作业
1. 已知二次函数y=-(x-4)2+4.
(1)写出其图象的开口方向,对称轴和顶点坐标;
(2)x取何值时,①y=0,②y>0,③y<0.
解:(1)∵二次函数y=-(x-4)2+4中,a=-1<0,
∴抛物线开口向下,对称轴为直线x=4,
顶点坐标为(4,4).
(2)当y=0时,-(x-4)2+4=0,
解得x=2或x=6.
①x=2或x=6时,y=0;
②2<x<6时,y>0;③x<2或x>6时,y<0.
2.如图X2-2-6,抛物线y=2(x-2)2-6的顶点为C,且一次函数y=-kx+3的图象经过点C,求这个一次函数的图象与两坐标轴所围成的三角形的面积.
解:根据题意,得点C的坐标为(2,-6),
由y=-kx+3的图象经过点C,
得-6=-2k+3,解得k= ,∴y=- x+3.
从而得此一次函数图象与两坐标轴的
交点坐标分别为 ,(0,3),
∴一次函数图象与两坐标轴所围成三角形的面积为 ×3=1.
3. 已知二次函数y= (x+1)2+4.
(1)写出抛物线的开口方向,顶点坐标和对称轴.
(2)画出此函数的图象,并说出此函数图象与y= x2的图象的关系.
解:(1)抛物线的开口方向向上,顶点坐标为(-1,4),对称轴为直线x=-1.
(2)如答图X2-2-4.
将二次函数y= (x+1)2+4的图象向右平移1个单位,再向下平移4个单位可得到y= x2的图象.
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
数学北师大版
九年级
二次函数的图象与性质
第3课时 y=ax2与y=a(x-h)2的二次函数的图象和性质.
1.函数 的图象的顶点坐标是 ;
开口方向是 ;最 值是 .
2.函数y=-2x2+3的图象可由函数y=-2x2的图象向 平移 个单位得到.
3.把函数y=-3x2的图象向下平移2个单位可得到函数
__________的图象.
(0,3)
向上
小
3
上
3
y=-3x2-2
二次函数y=ax2与y=ax2+c的图象有什么关系?
二次函数y=ax2+c的图象可以由 y=ax2 的图象
当c > 0 时 向上平移c个单位得到.
当c < 0 时 向下平移-c个单位得到.
函数
y=ax2+c
y=ax2
开口方向
a>0时,向上
a<0时,向下
对称轴
y轴
y轴
顶点坐标
(0,0)
(0,c)
a>0时,向上
a<0时,向下
上正下负
1、完成下表
x -3 -2 -1 0 1 2 3 4
y=3x?
y=3(x-1)?
27 12 3 0 3 12 27
函数y=3(x-1)?的图像是什么?
它与y=3x?的图像有什么关系?
比较y=3x?和y=3(x-1)?的值,它们之间有什么关系?
y=3(x-1)?的值比y=3x?的值落后
想一想:
27
27
12
12
3
3
0
0
12
12
27
27
新知导入
在下列平面直角坐标系中,做出y=3x?和y=3(x-1)?的图像
x -2 -1 0 1 2 3
y=3x? 12 3 0 3 12
y=3(x-1)? 12 3 0 3 12
(1)函数y=3(x-1)2的图象与y=3x2的图象有什么关系?
把y=3x?的图像沿x轴向右平移1个单位就得到y=3(x-1)?的图像
新知讲解
y=3x?,y=3(x-1)?的开口方向,对称轴,顶点坐标分别是什么?
抛物线 y=3x? y=3(x-1)?
开口方向
对称轴
顶点坐标
向上
向上
y轴或说x=0
x=1
(0,0)
(1,0)
当x取哪些值时, y随着x的增大而增大.
当x取哪些值时, y随着x的增大而增大.
y=3x?,x>0,
y=3(x-1)?,x>1
y=3x?,x<0,
y=3(x-1)?,x<1
思考:把y=3x?图象向左移1个单位应得到什么函数?
y=(3x-1)?
y=3x?
y=3(x+1)?
y=(3x-1)?
y=3x?
y=3x?,y=3(x-1)?,y=3(x+1)?
这三个函数图象有什么相同点?有什么不同点?
二次函数y=3x?,y=3(x-1)?,
y=(3x+1)?
的图象都是抛物线,并且形状相同,
只是位置不同.将函数y=3x?的图象向右平移1个单位长度,就得到函数y=(3x-1)?的图象;将的数y=3x?的图象向左平移1个单位长度,就得到函效y=(3x+1)?的图象.
将函数 y=2x?的图象向右平移1个单位, 就得到 y=2(x-1)?的图象;
若向左平移2个单位,得到函数 y=2(x+1)?的图象.
相同点: (1)图像都是抛物线,形状、大小相同,开口方向相同.
(2)都是轴对称图形.
(3)顶点都是最低点.
(4) 在对称轴左侧,都随 x 的增大而减小,在对称轴 右侧,都随 x 的增大而增大.
(5)它们的增长速度相同.
不同点: (1)对称轴不同. (2)顶点不同.
比较y=2x?, y=2(x-1)?,y=2(x+1)?的图象;
(6)最小值不同.
可得到函数y=a(x-h)2的图象
对称轴是直线x=h ;
顶点是(h ,0)
函数y=ax2的图象
向右平移h(h﹥0)个单位
(向左平移︱h︱(h﹤0)个单位)
函数y=a(x-h)2的图象:
0
x
y
(h ,0)
函数y=ax2与y=a(x-h)2的图象关系:
【归纳小结】
(h ,0)
左加右减
1.抛物线y=3x2-4与抛物线y =3x2 的_______相同,
_________不同.
2.抛物线y =3(x-1)2与抛物线y =3x2 的______相同,
_________不同.
3.抛物线y =3x2+5的开口_______,对称轴是______,
顶点坐标是____________.
4.抛物线y =-2(x+1)2的开口__________,对称轴是___________,顶点坐标是_____________.
形状
形状
位置
位置
向上
向下
y 轴
直线x =-1
(0,5)
(-1,0)
【跟踪训练】
5.将抛物线y=-x2向左平移2个单位后,得到的抛物线的解析式是( ).
o
y
x
1、画出二次函数y=3(x-1)2+2的图象,
2、并与二次函数y=3x2的图象进行比较,说明它们之间的关系.
函数y=3x2 的图象
向上平移
2个单位
函数y=3x2+2 的图象
向右平移
1个单位
向右平移
1个单位
函数y=3(x-1)2 的图象
向上平移
2个单位
函数y=3(x-1)2 +2的图象
再看下课本上的:在同一坐标系中作出二次函数y=2x?-1/2, y=2(x+3)2和y=2(x+3)2-1/2的图象.
二次函数y=2x?-1/2 , y=2(x+3)2和y=2(x+3)2-1/2的图象有什么关系?它们的开口方向,对称轴和顶点坐标分别是什么?
1.
2.
3.
-1
-2
-3.
0.
1.
2.
3.
4.
-1
x
y
5
y=2(x+3)2
y=2x2
y=2(x+3)2 -1/2
1.
2.
3.
-1
-2
-3.
0.
1.
2.
3.
4.
-1
x
y
5
y=2(x+3)2
y=2x2
y=2(x+3)2 -1/2
函数y=3x?的图象
o
y
x
向上平移2个单位
向右平移1个单位
练一练: 由二次函数y=3x?的图象,你能得到二次函数y=3x?+2,
y=3(x-1)?,y=3(x-2)?-5的图象吗?
y=3x?+2的图象
y=(3x-1)?的图象
y=3x?向右移平移2个单位,
再向下平移5个单位
可得y=3(x-2)?-5的图象
y=3x?向下平移5个单位
再向右移平移2个单位,
可得y=3(x-2)?-5的图象
对称轴:直线x= h
顶点: (h,k)
【规律方法】
(当k,h都大于0时)的图象特点
y=ax2的图象
向右平移
h个单位
y=a(x-h)2的图象
向上平移
k 个单位
y=a(x-h)2+k的图象
y=ax2+k的图象
向上平移
k 个单位
向右平移
h个单位
y=a(x-h)2+k的图象一条抛物线,
a>0开口向上,a<0开口向下
议一议:二次函数y=a(x-h)2+k 的图象与y=ax2 有什么关系?
y=ax2+bx+c的二次函数平移时,a的大小不会变
顶点坐标
对称轴
开口方向
抛物线
向上
向上
向上
向上
向上
向下
向下
y 轴(或x=0)
y 轴(x=0)
直线x=-1
直线x=1
直线x=1
直线x=-1
直线x=h
(h ,k)
(1,2)
(-1,-2)
(1,-2)
(-1,2)
(0,2)
(0,0)
【跟踪训练】
y=x2
y=3x2
y=5x2+2
y=(x-1)2+2
y=2(x+1)2+2
y=-(x-1)2+2
y=a(x-h)2+k
(a<0)
y=a(x-h)2+k 开口方向 对称轴 顶点坐标
a>0
a<0
向上
直线x=h
(h,k)
向下
直线x=h
(h,k)
1.y=a(x-h)2+k的图象的特征.
2.y=a(x-h)2+k的图象与y=ax2的图象的关系.
上加下减
左加右减
抛物线 有如下特点:
(1)当 a>0 时,开口向上;当 a<0 时,开口向下.
(2)对称轴为直线 x = h.
(3)顶点坐标(h,k).
(4)如果 a>0,当 x<h 时,y 随 x 的增大而减小,当 x>h 时,y 随 x 的增大而增大;
如果 a<0,当 x<h 时,y 随 x 的增大而增大,当 x>h 时,y 随 x 的增大而减小.
(5)当 a>0 时,y 有最小值k(即y ≥k);当 a<0 时,y 有最大值k(即y ≤k)
y = a(x - h)2 + k
课后作业
1. 已知二次函数y=-(x-4)2+4.
(1)写出其图象的开口方向,对称轴和顶点坐标;
(2)x取何值时,①y=0,②y>0,③y<0.
解:(1)∵二次函数y=-(x-4)2+4中,a=-1<0,
∴抛物线开口向下,对称轴为直线x=4,
顶点坐标为(4,4).
(2)当y=0时,-(x-4)2+4=0,
解得x=2或x=6.
①x=2或x=6时,y=0;
②2<x<6时,y>0;③x<2或x>6时,y<0.
2.如图X2-2-6,抛物线y=2(x-2)2-6的顶点为C,且一次函数y=-kx+3的图象经过点C,求这个一次函数的图象与两坐标轴所围成的三角形的面积.
解:根据题意,得点C的坐标为(2,-6),
由y=-kx+3的图象经过点C,
得-6=-2k+3,解得k= ,∴y=- x+3.
从而得此一次函数图象与两坐标轴的
交点坐标分别为 ,(0,3),
∴一次函数图象与两坐标轴所围成三角形的面积为 ×3=1.
3. 已知二次函数y= (x+1)2+4.
(1)写出抛物线的开口方向,顶点坐标和对称轴.
(2)画出此函数的图象,并说出此函数图象与y= x2的图象的关系.
解:(1)抛物线的开口方向向上,顶点坐标为(-1,4),对称轴为直线x=-1.
(2)如答图X2-2-4.
将二次函数y= (x+1)2+4的图象向右平移1个单位,再向下平移4个单位可得到y= x2的图象.
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
