北师大版九年级数学下册课件:2.2 第2课时 二次函数y=ax2和y=ax2+c的图象与性质(32张)
文档属性
| 名称 | 北师大版九年级数学下册课件:2.2 第2课时 二次函数y=ax2和y=ax2+c的图象与性质(32张) |  | |
| 格式 | zip | ||
| 文件大小 | 2.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-21 15:39:05 | ||
图片预览







文档简介
课件32张PPT。2.2 二次函数的图象与性质第二章 二次函数第2课时 二次函数y=ax2和y=ax2+c的图象与性质学习目标1.会画二次函数y=ax2和y=ax2+c的图象.(难点)
2.掌握二次函数y=ax2和y=ax2+c的性质并会应用.(重点)
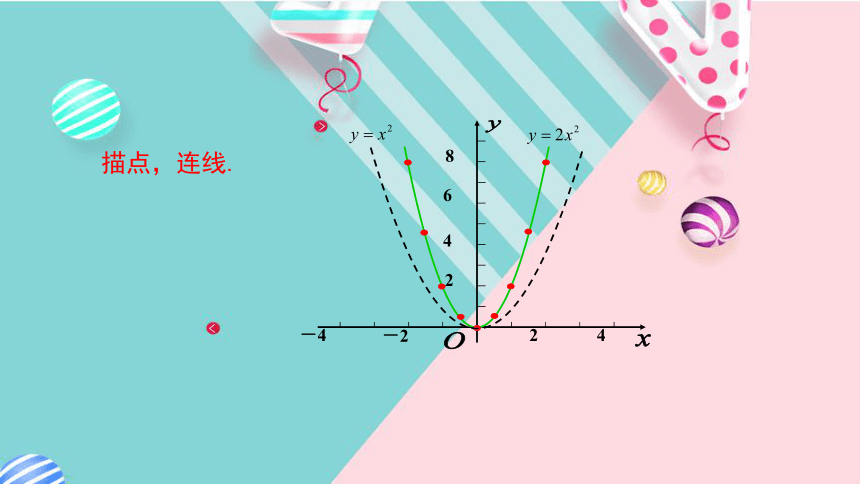
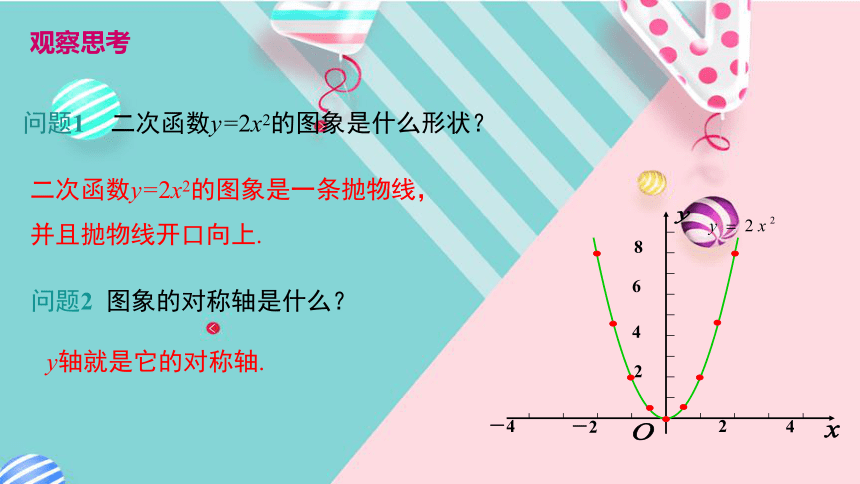
3.比较函数y=ax2与y=ax2+c的联系.导入新课门禁反映了图形的平移,大家还记得平移的要点吗?羽毛球的运动轨迹可以用y=ax2的图象刻画,大家能回忆出二次函数y=x2的性质吗?如果二次函数y=ax2的图象与平移碰撞在一起,会擦出怎样的火花呢?让我们拭目以待吧!情境引入讲授新课列表.4.520.504.520.5二次函数y=ax2的图象与性质合作探究描点,连线.问题1 二次函数y=2x2的图象是什么形状?二次函数y=2x2的图象是一条抛物线,
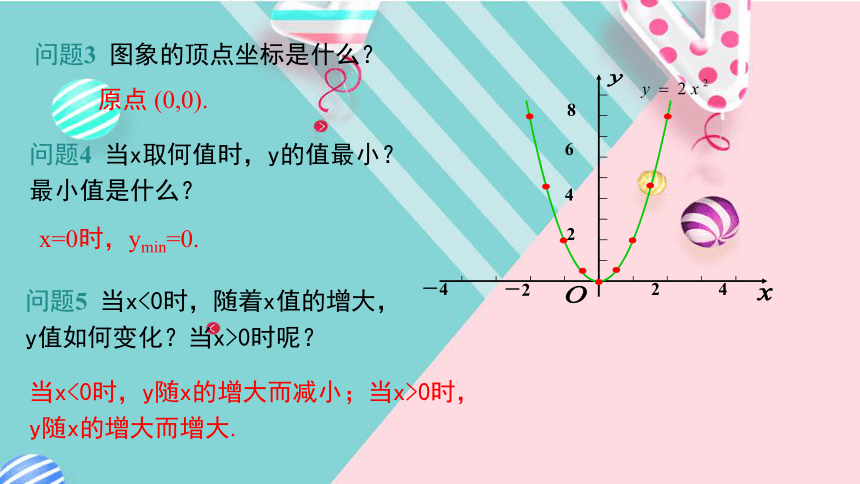
并且抛物线开口向上.问题2 图象的对称轴是什么?y轴就是它的对称轴.观察思考问题3 图象的顶点坐标是什么?原点 (0,0).问题4 当x取何值时,y的值最小?
最小值是什么?x=0时,ymin=0.当x<0时,y随x的增大而减小;当x>0时,y随x的增大而增大.问题5 当x<0时,随着x值的增大,
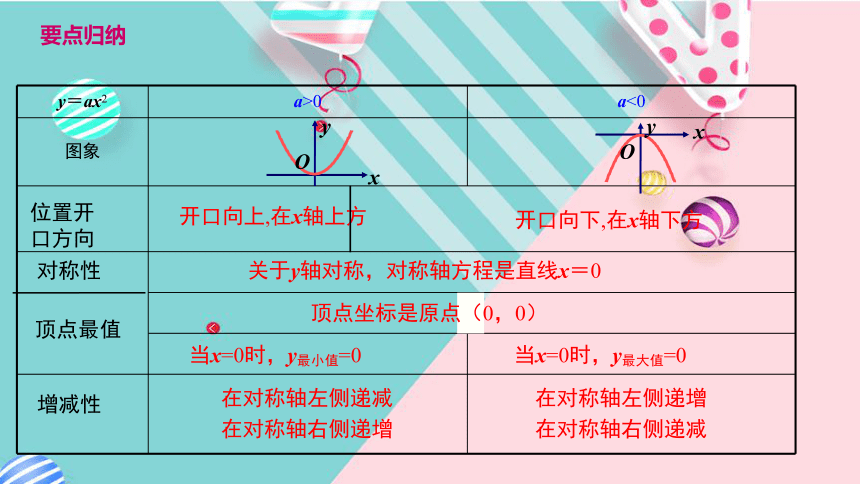
y值如何变化?当x>0时呢?位置开
口方向对称性顶点最值增减性开口向上,在x轴上方开口向下,在x轴下方关于y轴对称,对称轴方程是直线x=0当x=0时,y最小值=0当x=0时,y最大值=0在对称轴左侧递减
在对称轴右侧递增在对称轴左侧递增
在对称轴右侧递减顶点坐标是原点(0,0)要点归纳3.函数y= x2的图象的开口 ,对称轴是 ,顶点是 ;
顶点是抛物线的最____点.2.函数y=-3x2的图象的开口 ,对称轴是 ,顶点是_____ 顶点是抛物线的最____点1.函数y=4x2的图象的开口 ,对称轴是 ,顶点是 ; 向上 向下y轴y轴(0,0)(0,0)4.函数y= -0.2x2的图象的开口 ,
对称轴是_ __,顶点是 ; 向上y轴(0,0)向下y轴(0,0)高低练一练5.关于二次函数y=2x2,下列说法正确的是( )
A.它的开口方向是向下
B.当x<0时,y随x的增大而减小
C.它的对称轴是x=2
D.当x=0时,y有最大值是0B 例1 若点(x1,y1),B(x2,y2)是二次函数y=-3x2图象上的两点,
且x1>x2>0,那么y1与y2的大小关系是_____________.y2>y1典例精析分析: 是二次函数,即二次项的系数不为0,x的指数等于2.
又因当x>0时,y随x增大而增大,即说明二次项的系数大于0.
因此,解得 k=22当a>0时,a的绝对值越大,开口越小.合作探究当a<0时,a的绝对值越大,开口越小.在二次函数y=ax2中,a的绝对值越大,开口越小.要点归纳把图中图象的号码,填在它的函数式后面:(填序号)
(1)y=3x2的图象是_______;
(2)y= x2的图象是_______;
(3)y=-x2的图象是_______;
(4)y= x2的图象是_______.③①④②针对训练做一做:在同一直角坐标系中,画出二函数 y=2x2+1与y=2x2-1的图象.解:先列表:95.53135.5973.51-113.57 再描点,连线二次函数y=ax2+c的图象与性质合作探究y = 2x2+1y = 2x2-1问题:抛物线 y=2x2+1,y=2x2-1与抛物线y=2x2 有什么关系? 可以发现,把抛物线y=2x2 向 平移1个单位长度,就得到抛物线 ;把抛物线 y=2x2 向 平移1个单位长度,就得到抛物线 y=2x2-1. 下y=2x2+1上二次函数y=ax2+c的图象可以由 y=ax2 的图象平移得到:
当c > 0 时,向上平移c个单位长度得到.
当c < 0 时,向下平移-c个单位长度得到.二次函数y=ax2 与y=ax2+c(a ≠ 0)的图象的关系上下平移规律:
平方项不变,常数项上加下减.要点归纳二次函数y=-3x2+1的图象是将( )
A.抛物线y=-3x2向左平移3个单位得到
B.抛物线y=-3x2向左平移1个单位得到
C.抛物线y=3x2向上平移1个单位得到
D.抛物线y=-3x2向上平移1个单位得到D练一练问题 抛物线y=2x2+1,y=2x2-1的开口方向、对称轴和顶点各是什么? 二次函数开口方向顶点
坐标对称
轴向上向上(0,1)(0,-1)y轴y轴向上(0,0)y轴合作探究问题 抛物线y=2x2+1,y=2x2-1的增减性又如何? 当x=0时,y最小值=0当x<0时,y随x的增大而减小;
当x>0时,y随x的增大而增大.二次函数 y=ax2+c的性质向上向下直线x=0直线x=0(0,c)当x=0时,y最小值=c当x=0时,y最大值=c当x<0时,y随x的增大而减小;x>0时,y随x的增大而增大.当x>0时,y随x的增大而减小;x<0时,y随x的增大而增大.(0,c)要点归纳想一想
1.画抛物线y=ax2+c的图象有些方法?2.抛物线y=ax2+c 中的a决定什么?c决定什么?它的对称轴是什么?顶点坐标怎样表示?第一种方法:平移法,两步即第一步画y=ax2的图象,再向上(或向下)平移︱c ︱单位.第二种方法:描点法,三步即列表、描点和连线.a决定开口方向和大小;c决定顶点的纵坐标.
对称轴为y轴;顶点坐标为(0,c).例3:如图,抛物线y=x2-4与x轴交于A、B两点,点P为抛物线上一点,且S△PAB=4,求P点的坐标.解:抛物线y=x2-4,令y=0,得到x=2或-2,
即A点的坐标为(-2,0),B点的坐标为(2,0),
∴AB=4.
∵S△PAB=4,设P点纵坐标为b,
∴ ×4|b|=4,∴|b|=2,即b=2或-2.
当b=2时,x2-4=2,解得x=± ,
此时P点坐标为( ,2),(- ,2);
当b=-2时,x2-4=-2,解得x=± ,
此时P点坐标为( ,2),(- ,2).当堂练习1.抛物线y=2x2向下平移4个单位,就得到抛物
线 . 2.填表:y = 2x2-4向上向上向下(0,0)(0,1)(0,-5)y轴y轴y轴有最低点有最低点有最高点3.已知(m,n)在y=ax2+a(a不为0)的图象上,(-m,n) ___(填“在”或“不在”)y=ax2+a(a不为0)的图象上.
4. 若y=x2+(k-2)的顶点是原点,则k____;
若顶点位于x轴上方,则k____;若顶点位于x轴下方,则k .在=2>2<25.不画函数y=-x2和y=-x2+1的图象回答下面的问题:(1)抛物线y=-x2+1经过怎样的平移才能得到抛物线y=-x2.(2)函数y=-x2+1,当x 时, y随x的增大而减小;当x 时,函数y有最大值,最大值y是 ,其图象与y轴的交点坐标是 ,与x轴的交点坐标是 .(3)试说出抛物线y=x2-3的开口方向、对称轴和顶点坐标.向下平移1个单位.>0=01(0,1)(-1,0),(1,0)开口方向向上,对称轴是y轴,顶点坐标(0,-3).6.在平面直角坐标系xOy中,函数y=2x2的图象经过点M(x1,y1),
N(x2,y2)两点,若-4<x1<-2,0<x2<2,
则y1与y2的大小关系是__________.y1>y27.在同一直角坐标系中,一次函数y=ax+c和二次函数y=ax2+c的图象大致为( )方法总结:熟记一次函数y=kx+b在不同情况下所在的象限,以及熟练掌握二次函数的有关性质(开口方向、对称轴、顶点坐标等)是解决问题的关键.D8.已知 y =(m+1)x 是二次函数,且其图象开口向上,
求m的值和函数解析式m2+m解: 依题意有:m+1>0 ①m2+m=2 ②解②得:m1=-2, m2=1 由①得:m>-1∴ m=1 此时,二次函数为: y=2x2.二次函数y=ax2+c(a≠0)的图象和性质图象性质与y=ax2的关系开口方向由a的符号决定;
c决定顶点位置;
对称轴是y轴.增减性结合开口方向和对称轴才能确定.平移规律:
c正向上;
c负向下.课堂小结
2.掌握二次函数y=ax2和y=ax2+c的性质并会应用.(重点)
3.比较函数y=ax2与y=ax2+c的联系.导入新课门禁反映了图形的平移,大家还记得平移的要点吗?羽毛球的运动轨迹可以用y=ax2的图象刻画,大家能回忆出二次函数y=x2的性质吗?如果二次函数y=ax2的图象与平移碰撞在一起,会擦出怎样的火花呢?让我们拭目以待吧!情境引入讲授新课列表.4.520.504.520.5二次函数y=ax2的图象与性质合作探究描点,连线.问题1 二次函数y=2x2的图象是什么形状?二次函数y=2x2的图象是一条抛物线,
并且抛物线开口向上.问题2 图象的对称轴是什么?y轴就是它的对称轴.观察思考问题3 图象的顶点坐标是什么?原点 (0,0).问题4 当x取何值时,y的值最小?
最小值是什么?x=0时,ymin=0.当x<0时,y随x的增大而减小;当x>0时,y随x的增大而增大.问题5 当x<0时,随着x值的增大,
y值如何变化?当x>0时呢?位置开
口方向对称性顶点最值增减性开口向上,在x轴上方开口向下,在x轴下方关于y轴对称,对称轴方程是直线x=0当x=0时,y最小值=0当x=0时,y最大值=0在对称轴左侧递减
在对称轴右侧递增在对称轴左侧递增
在对称轴右侧递减顶点坐标是原点(0,0)要点归纳3.函数y= x2的图象的开口 ,对称轴是 ,顶点是 ;
顶点是抛物线的最____点.2.函数y=-3x2的图象的开口 ,对称轴是 ,顶点是_____ 顶点是抛物线的最____点1.函数y=4x2的图象的开口 ,对称轴是 ,顶点是 ; 向上 向下y轴y轴(0,0)(0,0)4.函数y= -0.2x2的图象的开口 ,
对称轴是_ __,顶点是 ; 向上y轴(0,0)向下y轴(0,0)高低练一练5.关于二次函数y=2x2,下列说法正确的是( )
A.它的开口方向是向下
B.当x<0时,y随x的增大而减小
C.它的对称轴是x=2
D.当x=0时,y有最大值是0B 例1 若点(x1,y1),B(x2,y2)是二次函数y=-3x2图象上的两点,
且x1>x2>0,那么y1与y2的大小关系是_____________.y2>y1典例精析分析: 是二次函数,即二次项的系数不为0,x的指数等于2.
又因当x>0时,y随x增大而增大,即说明二次项的系数大于0.
因此,解得 k=22当a>0时,a的绝对值越大,开口越小.合作探究当a<0时,a的绝对值越大,开口越小.在二次函数y=ax2中,a的绝对值越大,开口越小.要点归纳把图中图象的号码,填在它的函数式后面:(填序号)
(1)y=3x2的图象是_______;
(2)y= x2的图象是_______;
(3)y=-x2的图象是_______;
(4)y= x2的图象是_______.③①④②针对训练做一做:在同一直角坐标系中,画出二函数 y=2x2+1与y=2x2-1的图象.解:先列表:95.53135.5973.51-113.57 再描点,连线二次函数y=ax2+c的图象与性质合作探究y = 2x2+1y = 2x2-1问题:抛物线 y=2x2+1,y=2x2-1与抛物线y=2x2 有什么关系? 可以发现,把抛物线y=2x2 向 平移1个单位长度,就得到抛物线 ;把抛物线 y=2x2 向 平移1个单位长度,就得到抛物线 y=2x2-1. 下y=2x2+1上二次函数y=ax2+c的图象可以由 y=ax2 的图象平移得到:
当c > 0 时,向上平移c个单位长度得到.
当c < 0 时,向下平移-c个单位长度得到.二次函数y=ax2 与y=ax2+c(a ≠ 0)的图象的关系上下平移规律:
平方项不变,常数项上加下减.要点归纳二次函数y=-3x2+1的图象是将( )
A.抛物线y=-3x2向左平移3个单位得到
B.抛物线y=-3x2向左平移1个单位得到
C.抛物线y=3x2向上平移1个单位得到
D.抛物线y=-3x2向上平移1个单位得到D练一练问题 抛物线y=2x2+1,y=2x2-1的开口方向、对称轴和顶点各是什么? 二次函数开口方向顶点
坐标对称
轴向上向上(0,1)(0,-1)y轴y轴向上(0,0)y轴合作探究问题 抛物线y=2x2+1,y=2x2-1的增减性又如何? 当x=0时,y最小值=0当x<0时,y随x的增大而减小;
当x>0时,y随x的增大而增大.二次函数 y=ax2+c的性质向上向下直线x=0直线x=0(0,c)当x=0时,y最小值=c当x=0时,y最大值=c当x<0时,y随x的增大而减小;x>0时,y随x的增大而增大.当x>0时,y随x的增大而减小;x<0时,y随x的增大而增大.(0,c)要点归纳想一想
1.画抛物线y=ax2+c的图象有些方法?2.抛物线y=ax2+c 中的a决定什么?c决定什么?它的对称轴是什么?顶点坐标怎样表示?第一种方法:平移法,两步即第一步画y=ax2的图象,再向上(或向下)平移︱c ︱单位.第二种方法:描点法,三步即列表、描点和连线.a决定开口方向和大小;c决定顶点的纵坐标.
对称轴为y轴;顶点坐标为(0,c).例3:如图,抛物线y=x2-4与x轴交于A、B两点,点P为抛物线上一点,且S△PAB=4,求P点的坐标.解:抛物线y=x2-4,令y=0,得到x=2或-2,
即A点的坐标为(-2,0),B点的坐标为(2,0),
∴AB=4.
∵S△PAB=4,设P点纵坐标为b,
∴ ×4|b|=4,∴|b|=2,即b=2或-2.
当b=2时,x2-4=2,解得x=± ,
此时P点坐标为( ,2),(- ,2);
当b=-2时,x2-4=-2,解得x=± ,
此时P点坐标为( ,2),(- ,2).当堂练习1.抛物线y=2x2向下平移4个单位,就得到抛物
线 . 2.填表:y = 2x2-4向上向上向下(0,0)(0,1)(0,-5)y轴y轴y轴有最低点有最低点有最高点3.已知(m,n)在y=ax2+a(a不为0)的图象上,(-m,n) ___(填“在”或“不在”)y=ax2+a(a不为0)的图象上.
4. 若y=x2+(k-2)的顶点是原点,则k____;
若顶点位于x轴上方,则k____;若顶点位于x轴下方,则k .在=2>2<25.不画函数y=-x2和y=-x2+1的图象回答下面的问题:(1)抛物线y=-x2+1经过怎样的平移才能得到抛物线y=-x2.(2)函数y=-x2+1,当x 时, y随x的增大而减小;当x 时,函数y有最大值,最大值y是 ,其图象与y轴的交点坐标是 ,与x轴的交点坐标是 .(3)试说出抛物线y=x2-3的开口方向、对称轴和顶点坐标.向下平移1个单位.>0=01(0,1)(-1,0),(1,0)开口方向向上,对称轴是y轴,顶点坐标(0,-3).6.在平面直角坐标系xOy中,函数y=2x2的图象经过点M(x1,y1),
N(x2,y2)两点,若-4<x1<-2,0<x2<2,
则y1与y2的大小关系是__________.y1>y27.在同一直角坐标系中,一次函数y=ax+c和二次函数y=ax2+c的图象大致为( )方法总结:熟记一次函数y=kx+b在不同情况下所在的象限,以及熟练掌握二次函数的有关性质(开口方向、对称轴、顶点坐标等)是解决问题的关键.D8.已知 y =(m+1)x 是二次函数,且其图象开口向上,
求m的值和函数解析式m2+m解: 依题意有:m+1>0 ①m2+m=2 ②解②得:m1=-2, m2=1 由①得:m>-1∴ m=1 此时,二次函数为: y=2x2.二次函数y=ax2+c(a≠0)的图象和性质图象性质与y=ax2的关系开口方向由a的符号决定;
c决定顶点位置;
对称轴是y轴.增减性结合开口方向和对称轴才能确定.平移规律:
c正向上;
c负向下.课堂小结
