北师大版九下数学第2章二次函数全章热门考点整合应用课件(51张)
文档属性
| 名称 | 北师大版九下数学第2章二次函数全章热门考点整合应用课件(51张) |  | |
| 格式 | zip | ||
| 文件大小 | 916.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-26 11:29:28 | ||
图片预览









文档简介
(共51张PPT)
全章热门考点整合应用
第2章 二次函数
BS版 九年级下
提示:点击 进入习题
答案显示
习题链接
见习题
D
C
1
2
3
4
见习题
5
见习题
见习题
见习题
见习题
6
7
8
见习题
9
见习题
10
见习题
三
C
11
12
13
见习题
14
见习题
15
全章热门考点
1.已知函数y=(m+3)xm2+4m-3+5是关于x的二次函数.
(1)求m的值.
全章热门考点
(2)当m为何值时,该函数图象的开口向上?
解:∵函数图象的开口向上,∴m+3>0.∴m>-3.
∴m=1.∴当m=1时,该函数图象的开口向上.
(3)当m为何值时,该函数有最大值?
解:∵函数有最大值,∴m+3<0,∴m<-3.
∴m=-5.∴当m=-5时,该函数有最大值.
全章热门考点
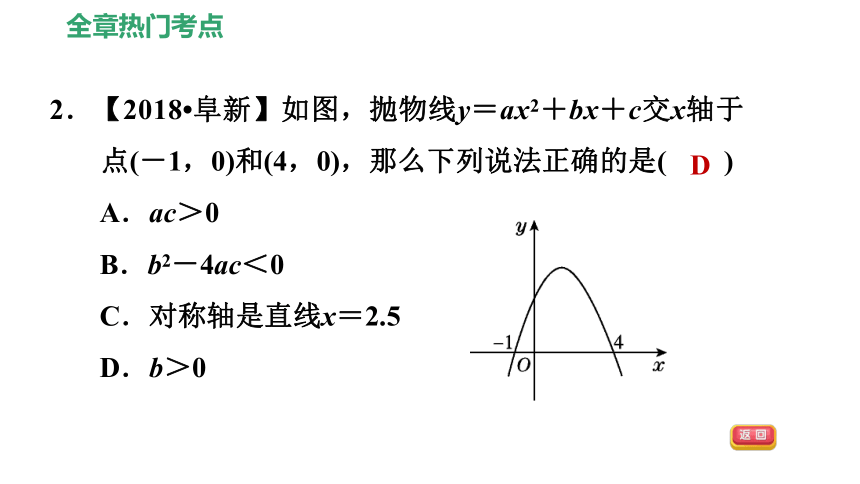
2.【2018?阜新】如图,抛物线y=ax2+bx+c交x轴于点(-1,0)和(4,0),那么下列说法正确的是( )
A.ac>0
B.b2-4ac<0
C.对称轴是直线x=2.5
D.b>0
D
全章热门考点
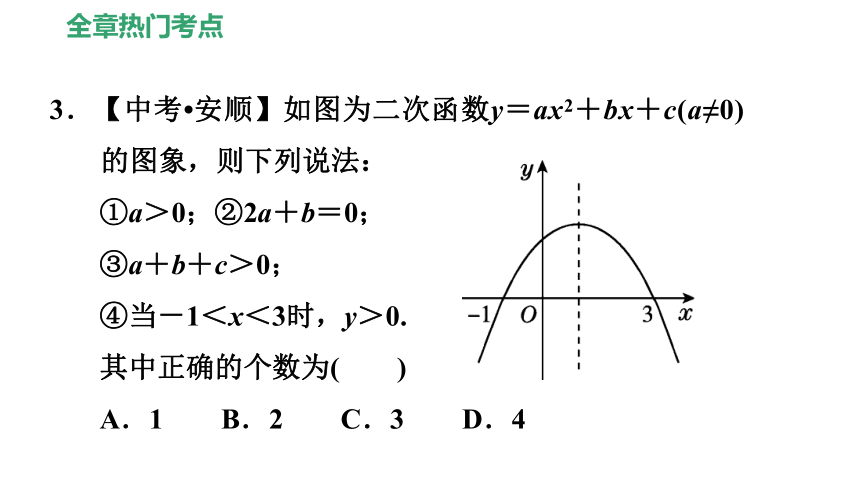
3.【中考?安顺】如图为二次函数y=ax2+bx+c(a≠0)的图象,则下列说法:
①a>0;②2a+b=0;
③a+b+c>0;
④当-1<x<3时,y>0.
其中正确的个数为( )
A.1 B.2 C.3 D.4
全章热门考点
【答案】C
全章热门考点
4.【2018?乐山】已知关于x的一元二次方程mx2+
(1-5m)x-5=0(m≠0).
(1)求证:无论m为任何非零实数,此方程总有两个实数根.
证明:∵Δ=(1-5m)2-4m×(-5)=1+25m2-
10m+20m=25m2+10m+1=(5m+1)2≥0,
∴无论m为任何非零实数,此方程总有两个实数根;
全章热门考点
(2)若抛物线y=mx2+(1-5m)x-5与x轴交于A
(x1,0)、B(x2,0)两点,且|x1-x2|=6,求m的值.
全章热门考点
(3)若m>0,点P(a,b)与Q(a+n,b)在(2)中的抛物线上(点P,Q不重合),求代数式4a2-n2+8n的值.
全章热门考点
5.如图,有长为24 m的栅栏,一面利用墙(墙的最大可用长度为10 m),围成中间隔有一道栅栏的长方形鸡舍(栅栏厚度不计).设鸡舍的一边AB为xm,面积为S m2.
全章热门考点
(1)求S与x的函数关系式(不必写出x的取值范围).
解:∵AB=x m,
∴BC=(24-3x) m,
此时S=x(24-3x)=-3x2+24x.
全章热门考点
(2)如果围成面积为45m2的鸡舍,AB的长是多少米?
全章热门考点
(3)能围成面积比45m2更大的鸡舍吗?如果能,请求出最大面积;如果不能,请说明理由.
全章热门考点
6.跳绳时,绳甩到最高处时的形状是抛物线.正在甩绳的甲、乙两名同学拿绳的手间距(A与B间的水平距离)为6 m,到地面的距离AO和BD均为0.9 m,身高为1.4 m的小丽站在距点O的水平距离为1 m的点F处,绳子甩到最高处时刚好通过她的头顶点E.以点O为原点建立如图所示的
平面直角坐标系,设此抛
物线对应的函数表达式为
y=ax2+bx+0.9.
全章热门考点
(1)求该抛物线对应的函数表达式(不考虑自变量的取值范围);
全章热门考点
(2)如果小华站在O,D之间,且离点O的距离为3 m,当绳子甩到最高处时刚好通过他的头顶,请你算出小华的身高;
解:把x=3代入y=-0.1x2+0.6x+0.9,
得y=-0.1×32+0.6×3+0.9=1.8.
即小华的身高是1.8 m.
解:当y=1.4时,-0.1x2+0.6x+0.9=1.4.
解得x1=1,x2=5. ∴1<t<5.
全章热门考点
(3)如果身高为1.4 m的小丽站在O,D之间,且离点O的距离为tm,绳子甩到最高处时超过她的头顶,请结合图象,写出t的取值范围.
全章热门考点
全章热门考点
(1)求这条抛物线对应的函数表达式;
全章热门考点
全章热门考点
全章热门考点
全章热门考点
x 1 2 3 4 5 6 7 8 9 10 11 12
z 19 18 17 16 15 14 13 12 11 10 10 10
全章热门考点
(1)请你根据表格求出每件产品的利润z(元)与月份x(月)的关系式;
全章热门考点
(2)若月利润w(万元)=当月销售量y(万件)×当月每件产品的利润z(元),求月利润w(万元)与月份x(月)的关系式;
全章热门考点
全章热门考点
(3)当x为何值时,月利润w有最大值,最大值为多少?
解:当1≤x≤8时,w=-x2+16x+80=-(x-8)2+144,
∴当x=8时,w取得最大值,此时w=144;
当x=9时,w=121,当10≤x≤12时,w=-10x+200,
则当x=10时,w取得最大值,此时w=100,
综上可得,当x为8时,月利润w有最大值,最大值为144万元.
全章热门考点
全章热门考点
(1)求销售量n与第x天之间的函数关系式;
全章热门考点
(2)求在草莓上市销售的30天中,每天的销售利润y(元)与第x天之间的函数关系式(日销售利润=日销售额-日维护费);
全章热门考点
(3)求日销售利润y的最大值及相应的x.
全章热门考点
全章热门考点
10.如图,线段AB的长为2,点C为AB上一个动点,分别以AC,BC为斜边在AB的同侧作等腰直角三角形ACD和等腰直角三角形BCE,求DE长的最小值.
全章热门考点
全章热门考点
11.某市“建立社会主义新农村”工作组到某县大棚蔬菜生产基地指导菜农修建大棚种植蔬菜.通过调查得知平均修建每公顷大棚要用支架、农膜等材料费2.7万元;购置滴灌设备的费用(万元)与大棚面积(公顷)的平方成正比,比例系数为0.9;另外种植每公顷蔬菜需种子、化肥、农药等开支0.3万元.每公顷蔬菜年均可卖7.5万元.
全章热门考点
(1)某基地的菜农共修建大棚x公顷,当年收益(扣除修建和种植成本后)为y万元,写出y关于x的函数表达式.
解:y=7.5x-(2.7x+0.9x2+0.3x)=-0.9x2+4.5x.
全章热门考点
(2)除种子、化肥、农药投资只能当年使用外,其他设施3年内不需要增加投资仍可继续使用.如果按3年计算,是否修建大棚面积越大,收益就越大?如果不是,修建面积为多少时可以获得最大收益?请帮助工作组为基地修建大棚提一项合理化的建议.
全章热门考点
解:设3年内每年的平均收益为z万元,根据题意,
得z=7.5x-(0.9x+0.3x2+0.3x)=-0.3x2+6.3x=-0.3(x-10.5)2+33.075.
∴并不是修建大棚面积越大收益就越大,当修建面积为10.5公顷时可以获得最大收益.
建议:(答案不唯一)当大棚面积超过10.5公顷时,扩大面积会使收益下降,修建面积不宜盲目扩大.
全章热门考点
12.已知抛物线y=ax2+bx+c的位置如图,则点P(a,bc)在第________象限.
三
全章热门考点
13.【2019?天津】二次函数y=ax2+bx+c(a,b,c是常数,a≠0)的自变量x与函数值y的部分对应值如下表:
x … -2 -1 0 1 2 …
y=ax2+
bx+c … t m -2 -2 n …
全章热门考点
全章热门考点
全章热门考点
【答案】C
全章热门考点
14.如图,已知二次函数y=-x2+bx+3的图象与x轴的一个交点为A(4,0),与y轴交于点B.
(1)求此二次函数的表达式和点B的坐标.
全章热门考点
(2)在x轴上是否存在点P,使得△PAB为等腰三角形?若存在,求出点P的坐标;若不存在,请说明理由.
全章热门考点
全章热门考点
15.【中考?安徽】如图,二次函数y=ax2+bx的图象经过点A(2,4)与B(6,0).
(1)求a,b的值;
全章热门考点
(2)点C是该二次函数图象上A,B两点之间的一动点,横坐标为x(2<x<6),写出四边形OACB的面积S关于点C的横坐标x的函数表达式,并求S的最大值.
全章热门考点
全章热门考点
全章热门考点整合应用
第2章 二次函数
BS版 九年级下
提示:点击 进入习题
答案显示
习题链接
见习题
D
C
1
2
3
4
见习题
5
见习题
见习题
见习题
见习题
6
7
8
见习题
9
见习题
10
见习题
三
C
11
12
13
见习题
14
见习题
15
全章热门考点
1.已知函数y=(m+3)xm2+4m-3+5是关于x的二次函数.
(1)求m的值.
全章热门考点
(2)当m为何值时,该函数图象的开口向上?
解:∵函数图象的开口向上,∴m+3>0.∴m>-3.
∴m=1.∴当m=1时,该函数图象的开口向上.
(3)当m为何值时,该函数有最大值?
解:∵函数有最大值,∴m+3<0,∴m<-3.
∴m=-5.∴当m=-5时,该函数有最大值.
全章热门考点
2.【2018?阜新】如图,抛物线y=ax2+bx+c交x轴于点(-1,0)和(4,0),那么下列说法正确的是( )
A.ac>0
B.b2-4ac<0
C.对称轴是直线x=2.5
D.b>0
D
全章热门考点
3.【中考?安顺】如图为二次函数y=ax2+bx+c(a≠0)的图象,则下列说法:
①a>0;②2a+b=0;
③a+b+c>0;
④当-1<x<3时,y>0.
其中正确的个数为( )
A.1 B.2 C.3 D.4
全章热门考点
【答案】C
全章热门考点
4.【2018?乐山】已知关于x的一元二次方程mx2+
(1-5m)x-5=0(m≠0).
(1)求证:无论m为任何非零实数,此方程总有两个实数根.
证明:∵Δ=(1-5m)2-4m×(-5)=1+25m2-
10m+20m=25m2+10m+1=(5m+1)2≥0,
∴无论m为任何非零实数,此方程总有两个实数根;
全章热门考点
(2)若抛物线y=mx2+(1-5m)x-5与x轴交于A
(x1,0)、B(x2,0)两点,且|x1-x2|=6,求m的值.
全章热门考点
(3)若m>0,点P(a,b)与Q(a+n,b)在(2)中的抛物线上(点P,Q不重合),求代数式4a2-n2+8n的值.
全章热门考点
5.如图,有长为24 m的栅栏,一面利用墙(墙的最大可用长度为10 m),围成中间隔有一道栅栏的长方形鸡舍(栅栏厚度不计).设鸡舍的一边AB为xm,面积为S m2.
全章热门考点
(1)求S与x的函数关系式(不必写出x的取值范围).
解:∵AB=x m,
∴BC=(24-3x) m,
此时S=x(24-3x)=-3x2+24x.
全章热门考点
(2)如果围成面积为45m2的鸡舍,AB的长是多少米?
全章热门考点
(3)能围成面积比45m2更大的鸡舍吗?如果能,请求出最大面积;如果不能,请说明理由.
全章热门考点
6.跳绳时,绳甩到最高处时的形状是抛物线.正在甩绳的甲、乙两名同学拿绳的手间距(A与B间的水平距离)为6 m,到地面的距离AO和BD均为0.9 m,身高为1.4 m的小丽站在距点O的水平距离为1 m的点F处,绳子甩到最高处时刚好通过她的头顶点E.以点O为原点建立如图所示的
平面直角坐标系,设此抛
物线对应的函数表达式为
y=ax2+bx+0.9.
全章热门考点
(1)求该抛物线对应的函数表达式(不考虑自变量的取值范围);
全章热门考点
(2)如果小华站在O,D之间,且离点O的距离为3 m,当绳子甩到最高处时刚好通过他的头顶,请你算出小华的身高;
解:把x=3代入y=-0.1x2+0.6x+0.9,
得y=-0.1×32+0.6×3+0.9=1.8.
即小华的身高是1.8 m.
解:当y=1.4时,-0.1x2+0.6x+0.9=1.4.
解得x1=1,x2=5. ∴1<t<5.
全章热门考点
(3)如果身高为1.4 m的小丽站在O,D之间,且离点O的距离为tm,绳子甩到最高处时超过她的头顶,请结合图象,写出t的取值范围.
全章热门考点
全章热门考点
(1)求这条抛物线对应的函数表达式;
全章热门考点
全章热门考点
全章热门考点
全章热门考点
x 1 2 3 4 5 6 7 8 9 10 11 12
z 19 18 17 16 15 14 13 12 11 10 10 10
全章热门考点
(1)请你根据表格求出每件产品的利润z(元)与月份x(月)的关系式;
全章热门考点
(2)若月利润w(万元)=当月销售量y(万件)×当月每件产品的利润z(元),求月利润w(万元)与月份x(月)的关系式;
全章热门考点
全章热门考点
(3)当x为何值时,月利润w有最大值,最大值为多少?
解:当1≤x≤8时,w=-x2+16x+80=-(x-8)2+144,
∴当x=8时,w取得最大值,此时w=144;
当x=9时,w=121,当10≤x≤12时,w=-10x+200,
则当x=10时,w取得最大值,此时w=100,
综上可得,当x为8时,月利润w有最大值,最大值为144万元.
全章热门考点
全章热门考点
(1)求销售量n与第x天之间的函数关系式;
全章热门考点
(2)求在草莓上市销售的30天中,每天的销售利润y(元)与第x天之间的函数关系式(日销售利润=日销售额-日维护费);
全章热门考点
(3)求日销售利润y的最大值及相应的x.
全章热门考点
全章热门考点
10.如图,线段AB的长为2,点C为AB上一个动点,分别以AC,BC为斜边在AB的同侧作等腰直角三角形ACD和等腰直角三角形BCE,求DE长的最小值.
全章热门考点
全章热门考点
11.某市“建立社会主义新农村”工作组到某县大棚蔬菜生产基地指导菜农修建大棚种植蔬菜.通过调查得知平均修建每公顷大棚要用支架、农膜等材料费2.7万元;购置滴灌设备的费用(万元)与大棚面积(公顷)的平方成正比,比例系数为0.9;另外种植每公顷蔬菜需种子、化肥、农药等开支0.3万元.每公顷蔬菜年均可卖7.5万元.
全章热门考点
(1)某基地的菜农共修建大棚x公顷,当年收益(扣除修建和种植成本后)为y万元,写出y关于x的函数表达式.
解:y=7.5x-(2.7x+0.9x2+0.3x)=-0.9x2+4.5x.
全章热门考点
(2)除种子、化肥、农药投资只能当年使用外,其他设施3年内不需要增加投资仍可继续使用.如果按3年计算,是否修建大棚面积越大,收益就越大?如果不是,修建面积为多少时可以获得最大收益?请帮助工作组为基地修建大棚提一项合理化的建议.
全章热门考点
解:设3年内每年的平均收益为z万元,根据题意,
得z=7.5x-(0.9x+0.3x2+0.3x)=-0.3x2+6.3x=-0.3(x-10.5)2+33.075.
∴并不是修建大棚面积越大收益就越大,当修建面积为10.5公顷时可以获得最大收益.
建议:(答案不唯一)当大棚面积超过10.5公顷时,扩大面积会使收益下降,修建面积不宜盲目扩大.
全章热门考点
12.已知抛物线y=ax2+bx+c的位置如图,则点P(a,bc)在第________象限.
三
全章热门考点
13.【2019?天津】二次函数y=ax2+bx+c(a,b,c是常数,a≠0)的自变量x与函数值y的部分对应值如下表:
x … -2 -1 0 1 2 …
y=ax2+
bx+c … t m -2 -2 n …
全章热门考点
全章热门考点
全章热门考点
【答案】C
全章热门考点
14.如图,已知二次函数y=-x2+bx+3的图象与x轴的一个交点为A(4,0),与y轴交于点B.
(1)求此二次函数的表达式和点B的坐标.
全章热门考点
(2)在x轴上是否存在点P,使得△PAB为等腰三角形?若存在,求出点P的坐标;若不存在,请说明理由.
全章热门考点
全章热门考点
15.【中考?安徽】如图,二次函数y=ax2+bx的图象经过点A(2,4)与B(6,0).
(1)求a,b的值;
全章热门考点
(2)点C是该二次函数图象上A,B两点之间的一动点,横坐标为x(2<x<6),写出四边形OACB的面积S关于点C的横坐标x的函数表达式,并求S的最大值.
全章热门考点
全章热门考点
